CPML在3维HIE-FDTD 算法中的实现

李 建，刘宗信，王发年，李 斌，陈桂杰

（解放军95972部队 甘肃 酒泉 735018）

时域有限差分（FDTD）方法具有方法简单、适用性强等优点，已被广泛应用。然而，由于常规FDTD算法的时间步长受稳定性条件的限制，而时间步长的选取是由最小空间步长决定的[1]，这样小的步长会使迭代步数和模拟时间增加。1999年T.Namiki提出了一种新的交替方向隐格式时域有限差分算法（ADI-FDTD），该方法具有无条件稳定的特性，因而时间步长不再受稳定性条件的限制[2-3]。然而ADI-FDTD方法在一个时间步上需要两次迭代，增加了每步的计算时间和计算机的存储量，而且随着时间步的增大，数值色散变大，降低了数值模拟的精度。

为了克服以上算法的缺点，B.K.Huang等人提出了弱无条件稳定算法[4]。该方法是有条件稳定的，但其稳定性条件比常规FDTD要宽松，而且该方法比ADI方法有更高的计算精度，计算时间上也比ADI方法有优势。CFS-PML吸收边界以其简单、直观、高吸收性能（尤其在吸收凋落波方面）著称，一经提出就被广泛使用，但是该边界条件不便于实现。本文拟将CFS-PML技术引入到混合显隐式弱无条件稳定时域有限差分算法（HIE-FDTD）中，研究其具体差分格式、吸波性能及如何合理设置其复频率参数。

1 公式推导

借助辅助差分方程，可以将三维情形下，PML局域内的麦克斯韦方程表示如下：

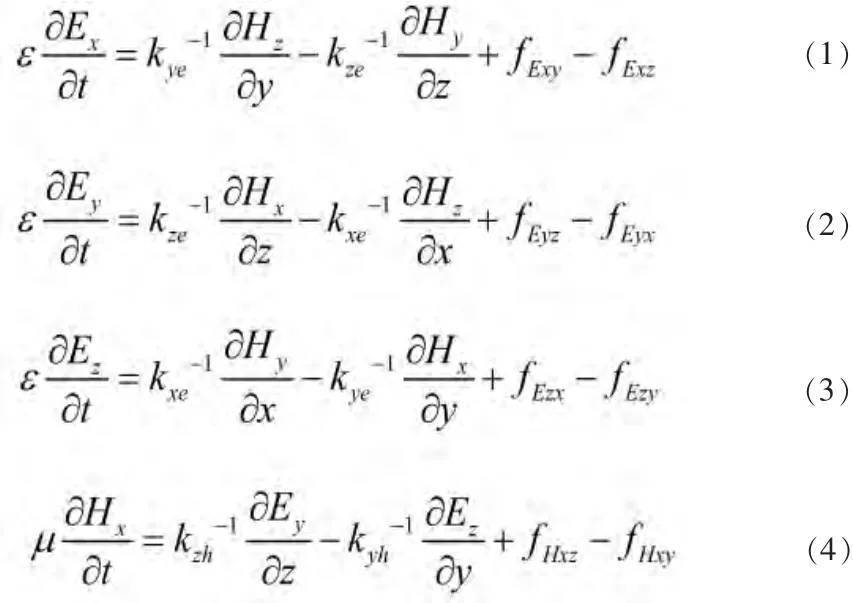
按照HIE方法[4]对式(1)～(6)进行差分离散可以得到：

其中，△t为时间步长，△x，△y，△z是 x轴、y轴和 z轴方向的网格大小。使用标准Yee格式对公式(7)～(18)中的辅助变量进行离散可以得到一系列差分方程，这里仅给出(7)的差分格式，其余各项按同样的方法均可得到。

从公式(19)～(24)和(25)可以看出，对于电场场量 Ey和 Hy可以直接更新得到。将未知磁场量(24)式代入(19)式中，连立(15)、(16)、(21)、(22) 可得一关于电场分量 Ex在 n+1 时间步的一个隐式迭代表达，如式(26)所示：

式(26)可以用Thomas方法解决，求解后可以通过显式直接更新。同理可以求得和。从上述公式可以看出，三维HIEFDTD方法在整个循环迭代过程中，需要解算2个三对角矩阵，进行4次显式迭代和12个辅助变量的运算。然而三维ADI-FDTD方法在整个循环迭代过程中，需要解算3个三对角矩阵，进行3次显式迭代和12个辅助变量的运算。显然，HIE-FDTD比ADI-FDTD有着更好的计算效率。

2 数值结果

为了验证CFS-PML在三维HIE-FDTD算法中的精确性和有效性，采用图1所示的几何模型，采用均匀空间步长划分△=△x=△y=△z=0.5 mm，网格为 66×66×66，每个方向上的CPML层均设置为8层用来截断计算局域[5]。观察点设置在A(57,33,33)点和B(57,57,33)。采用式(6)所示形式的高斯脉冲作为激烈源放在整个结构的正中间，其中：f0=1 GHz ，t0=1.0×10-10,τ=1.0×10-10。

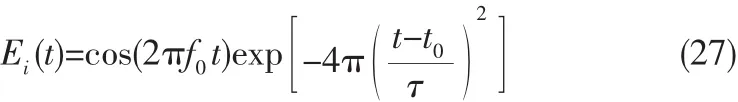
CPML层中的参数由式(7)确定，本文取m=4，α取固定值。

图1 数值示例的几何模型Fig.1 Geometry of the numerical example

为了便于比较，设立一266×266×266的参考空间，在观察点，关于时间函数的相对反射误差及各参数的含义同式(31)。

图2显示了在 HIE-FDTD中使用Mur吸收边界、在HIE-FDTD中使用CPML吸收边界以及在传统FDTD中使用CPML吸收边界时相对反射误差随时间的变化曲线。从图中显示的计算结果可以得出本文所提出的CPML吸收边界条件比一阶Mur吸收边界具有更好的吸波性能，在整个变化过程中，HIE-CPML比HIE-Mur的反射误差平均要低30 dB。

下面，我们来观察PML函数的基本构成变量κmax，σmax以及α与其最大反射误差的关系。图3、图4分别是α=0.05、α=0.003时κmax和σmax与反射误差的等高图。从图可以看出，当α=0.05、α=0.003 时，最大误差均为-72 dB，但当取 α=0.05，可以在一个较大范围内合理选取κmax和σmax来实现最佳误差，从而使得在选值时易于预测。显而易见，选取κmax=14、σmax/σopt=1.0就可以实现低至-72 dB的最大相对误差。

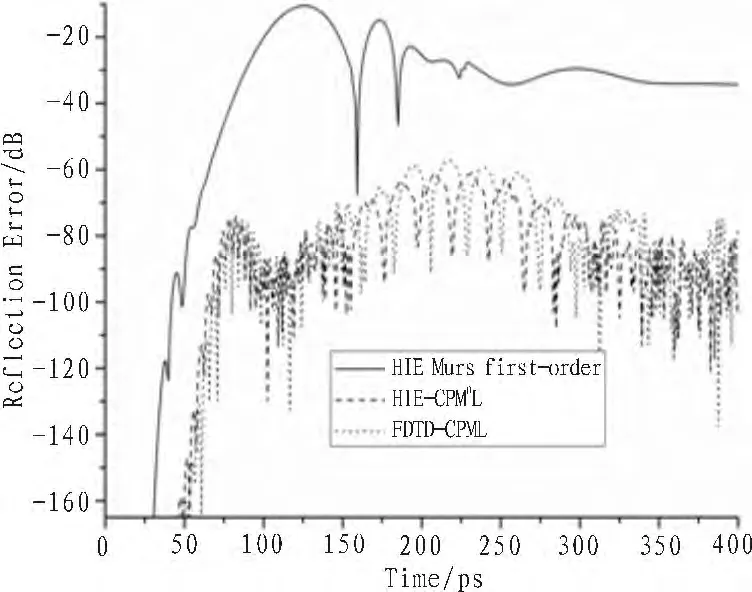
图2 不同方法的相对反射误差Fig.2 Relative reflection error for different methods

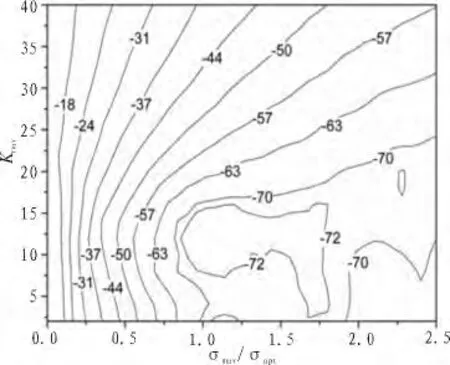
图3 α=0.05、m=4时观察点观测到的关于 κmax和 σmax/σopt函数的最大反射误差Fig.3 Maximum reflection error at observation point as a function of κmaxand σmax/σopt(α=0.05 and m=4)

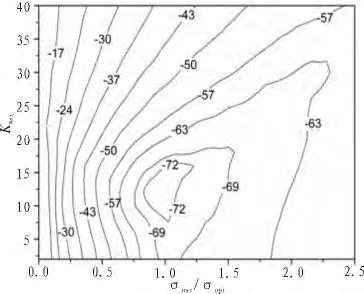
图4 α=0.003、m=4时观察点观测到的关于κmax和σmax/σopt函数的最大反射误差Fig.4 Maximum reflection error at observation point as a function of κmaxand σmax/σopt(α=0.003 and m=4)

3 结论

本文将坐标伸缩完全匹配层CPML引入到3维弱无条件稳定算法HIE-FDTD中研究其吸波性能。详细推导了CPML在3维HIE-FDTD算法中的差分公式，建立了计算模型，并将其与几种常用的吸收边界条件的吸波性能进行了综合比较。数值结果表明：当将本文所提方法的CPML层数设置为8时，其最大反射误差为-72 dB，远低于传统FDTD方法的反射误差。另外，当匹配层参数设置为α=0.05，可以在一个较大范围内合理选取κmax和σmax来实现最佳误差，从而使得在选值时易于预测反射情况。

[1]Taflove A，Hagness S C.Computational Electrodynamics:the Finite-DifferenceTime-domain Method[M].Boston,MA:Artech House,2000.

[2]Namiki T,Ito K.Numerical simulation using ADI-FDTD method to estimate shielding effectiveness of thin conductive enclosures[J].IEEE Trans.Microwave Theory Tech,2001,49(6)：1060-1066.

[3]Yuan C H,Chen Z Z.Toward accurate time-domain simulation of highly conductive materials[J].IEEE Trans.Microwave Theory Tech.-s Digest,2002,(WE4E-4):1135-1138.

[4]Binke Huang,Gang Wang,Yansheng Jiang.A Hybrid implicitexplicit FDTD scheme with weakly conditional stability[J].Microwave and Optical Tech.Lett,2003,39(2):97-101.

[5]LIU Zong-xin,CHEN Yi-wang,SUN Xue-gang,et al.Implementation of CFS-PML for HIE-FDTD Method[J].IEEE Antennas and Wireless Propagation Letters,2012(11)：381-384.

[6]Mao Y F,Chen B,Chen H L,et al.Unconditionally stable SFDTD algorithm for solving oblique incident wave on periodic structures[J].IEEE Microw.Wireless Comp.Lett.,2009,19(5):257-259.