黏性土填料下考虑土拱效应的挡土墙被动土压力计算

周晓龙，马 亢，钱 明，刘德稳，赵 琦

（1.杭州科技职业技术学院 城市建设学院，杭州 311402；2.厦门大学 土木工程系，福建 厦门 361005；3.中国石油天然气华东勘察设计研究院 岩土工程处，山东 青岛 266071；4.西南林业大学 土木工程学院，昆明 650000；5.北方工业大学 建筑工程学院，北京 100144）

1 引 言

计算挡土墙被动土压力的2个参数是被动土压力系数Kawn和竖向平均应力。众多的室内试验及模型测试表明[1-3]，挡土墙被动土压力呈非线性分布，并且与墙体的位移模式有较大的关系，传统的Rankine 及Coulomb 理论无法解释这种现象，为了解释这种现象及找到合适的计算理论，林宇亮等[4]、王元战等[5]分别采用水平层分析法对其进行了研究，但假定基底应力是均匀分布，未考虑主应力旋转的影响即土拱效应的影响。

土拱效应作为自然界常见的一种现象，自Terzaghi 通过著名的活动门试验后[6]，许多学者都致力于将土拱效应原理应用于求解挡土墙被动土压力，如彭述权等[7]、李永刚等[8]、吴明等[9]、侯键等[10]、王立国等[11]，这些研究主要集中于土拱效应在砂性土中的研究。

被动土压力系数的影响因素主要有土拱形状和滑裂面倾角。关于土拱现状的讨论于20 世纪80年代曾进行过较为详尽的讨论[12]，普遍认为土拱形状与圆弧均较为接近[13-14]。而滑裂面倾角的选择上多数学者[7,9,13-14]倾向于选择朗肯滑裂面倾角。竖向平均应力的求解主要有两种方法：一种是采用Rankine 的应力状态思想，类似于求解主动土压力时，如PAIK 等[13]、涂兵雄等[14]基于滑裂面处点的应力状态来计算。另一种方法采用Coulomb 的静力平衡思想，即基于水平微分层静力平衡法[7-11]。为了研究这两种方法的适用性，对比研究考虑土拱效应后的两种方法求解结果是必要的。

基于前面所述2个参数的计算方法，即可得到考虑土拱效应的挡土墙被动土压力计算方法，并可推导出被动土压力合力，作用点高度求解公式。

2 被动土压力系数

如图1 所示，坐标平移的方式，新旧坐标系的关系为

式中：σ′、σ 分别为正应力在新旧坐标系的值；σ0为黏结应力。

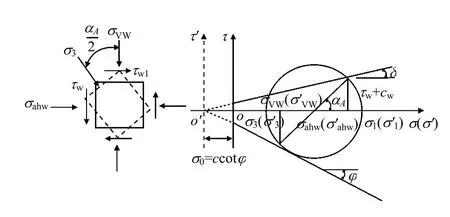
图1 挡土墙后土体应力摩尔圆Fig.1 Mohr circle for stress behind wall

大主应力轨迹线如图2 所示，分析时需要做如下假定：

（1）A 点处墙土摩擦力满足：

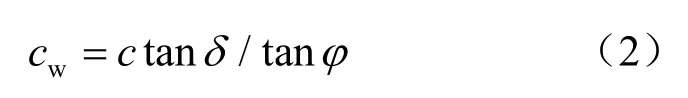
式中：cw为墙土黏聚力；c为黏聚力；φ为内摩擦角；δ为墙土摩擦角。

即满足：

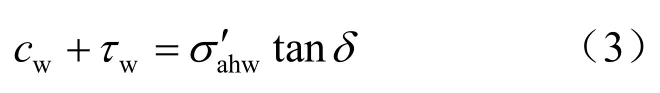
（2）滑裂面为直线，且倾角为满足朗肯分析结果，滑裂面β=π/4-φ/2。

被动土压力侧向土压力系数定义为

根据文献[9]的分析，点A 的应力状态为小主应力的偏转角：

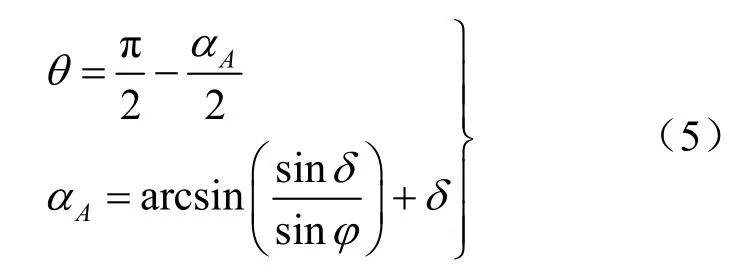
水平力在变换坐标系下

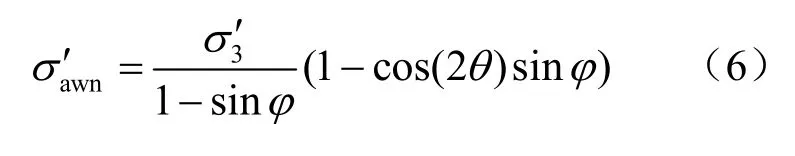
竖向力在变换坐标系下

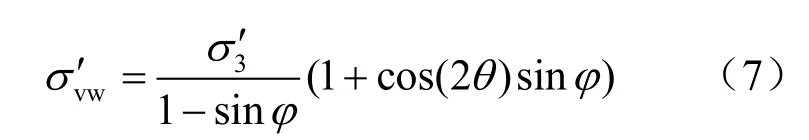
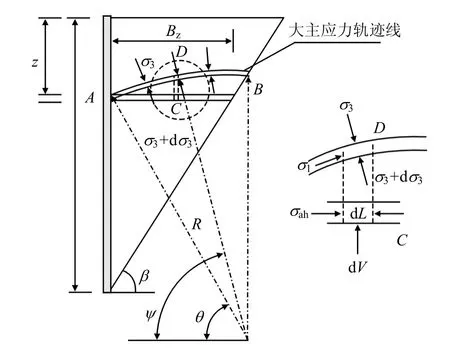
图2 挡土墙后大主应力轨迹线Fig.2 Trajectory of major principal stresses behind retaining wall

任意一点D 的竖向应力在变换坐标系下有

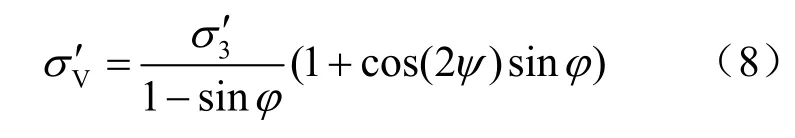
如图2 所示，D 点取宽度为dL，其竖向力为

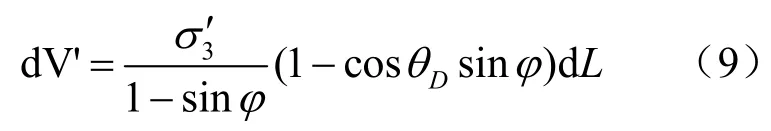
土拱的半径R为

则可知竖向平均应力在变换坐标系下有

式中：Kp为朗肯被动土压力系数，大小为tan2(π/4+φ/2)。由式（11）可知砂性土被动土压力侧向土压力系数定义为

退化为砂土时被动土压力侧向土压力系数为

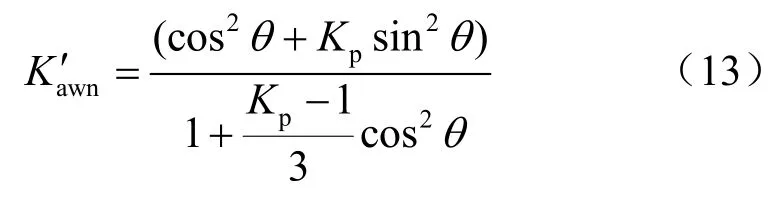
砂土与黏性土最大的区别在于黏性土侧向土压力系数沿着墙高不变，而黏性土是变化的。

3 竖向平均应力求解

3.1 应力状态法求解

应力状态法分析时将右侧三角形区域单独拿出来分析，右侧三角形区域已平衡，针对左侧建立微分方程式（14）即可。

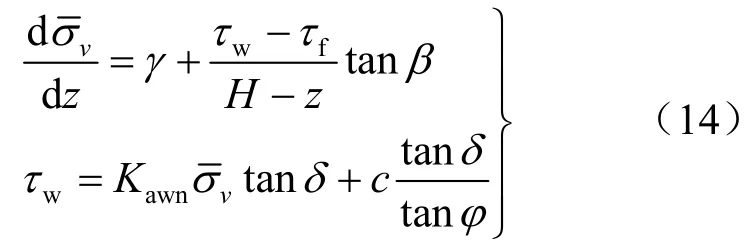
已知滑裂面倾角即已知该点应力状态，可知图3、4 中：

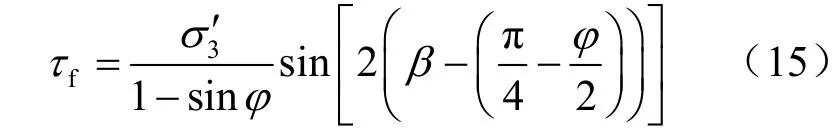
本文假定滑裂面为朗肯滑裂面β=π/4-φ/2，因而τf为0。

由于Kawn是关于z 的函数，而式（13）定义砂性土被动土压力系数，事实上也满足：

二者满足下面的关系：

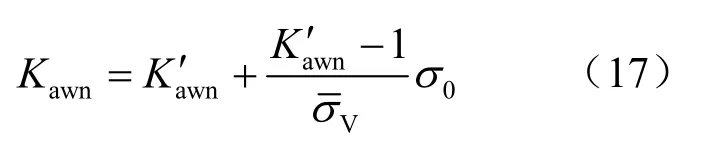
定义下式：

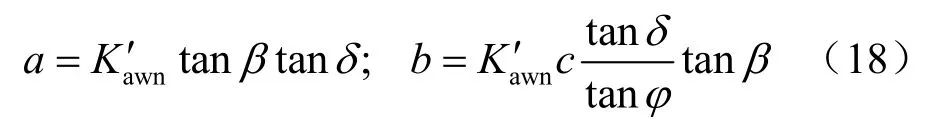
式（14）可写为

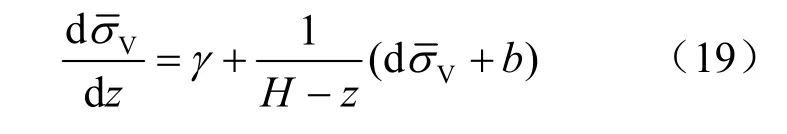
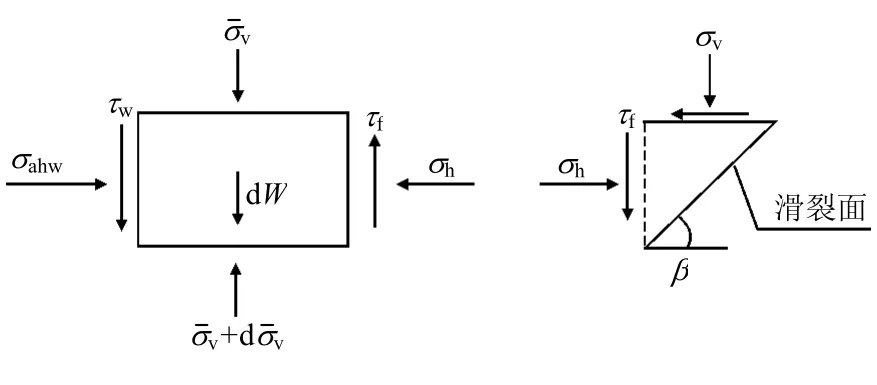
图3 水平微分单元应力状态法模型Fig.3 Analysis model for horizontal differential element behind retaining wall using stress state method

3.2 静力平衡法求解

水平向微分方程为

于彤在今年体重增加了20公斤，作为一名产后妈妈，她开始寻求各种能够迅速瘦身的方式。“生酮饮食”，引起了她的注意。理论上，生酮饮食是高脂肪、低碳水化合物的配方饮食。上世纪20年代，美国医生通过禁食但不禁水的方法治疗癫痫患儿，有不少患儿长时间没有再发作。这被认为模拟了饥饿的代谢效果而被用于临床医疗。这样的饮食方式后来被移植到减肥领域。只吃瘦肉和蔬菜，不吃含有碳水化合物的主食，以此产生大量酮体，迫使身体燃烧脂肪。“不用吃药，吃的都是很正常的食物。”于彤说。

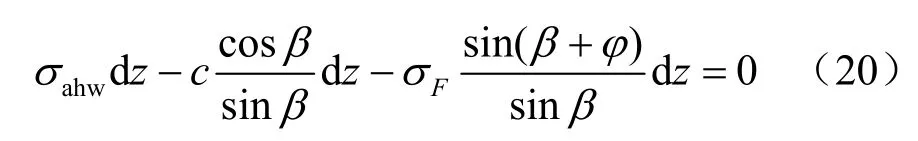
竖向微分方程为

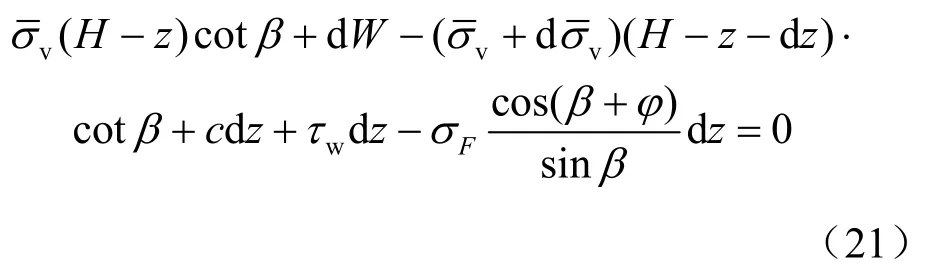
式中：切应力计算公式为

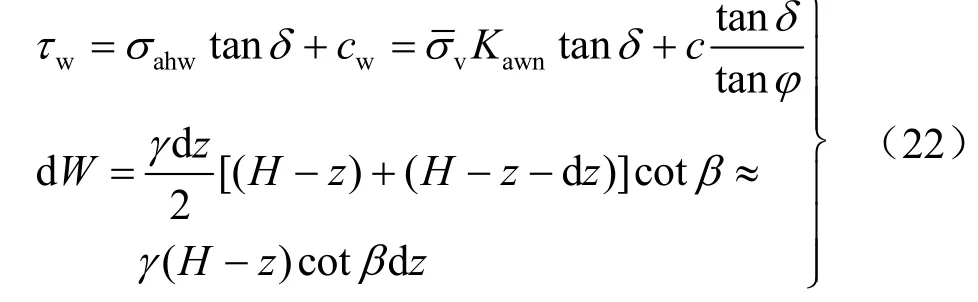
由式（20）可得

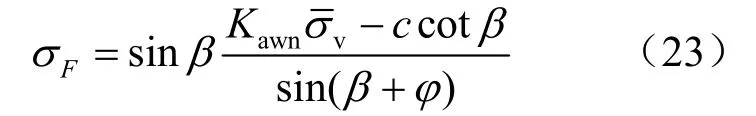
将式（22），（23）代入式（21），可得

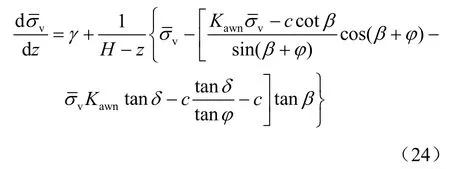
定义下式：

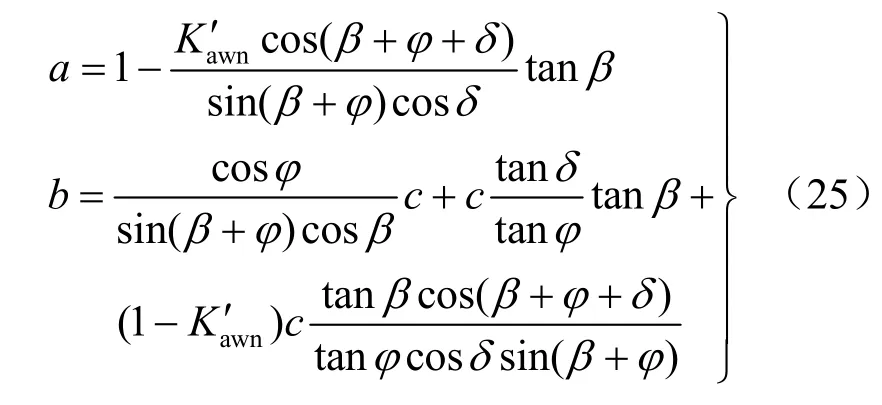
式（24）也可写为

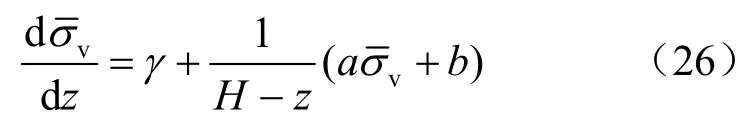
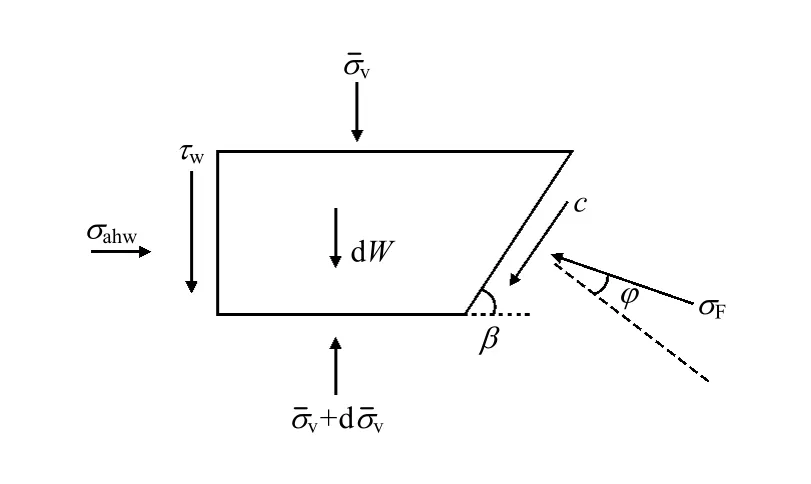
图4 水平微分单元水平静力平衡法模型Fig.4 Analysis model for horizontal differential element behind retaining wall using horizontal static equilibrium method

3.3 基于统一表达式下的解

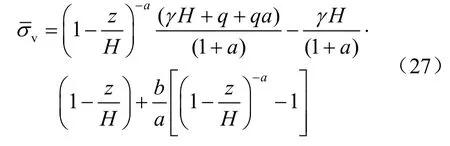
根据式（27），平均竖向应力乘以侧向土压力系数可得任意深度z 处的水平向主动土压力为

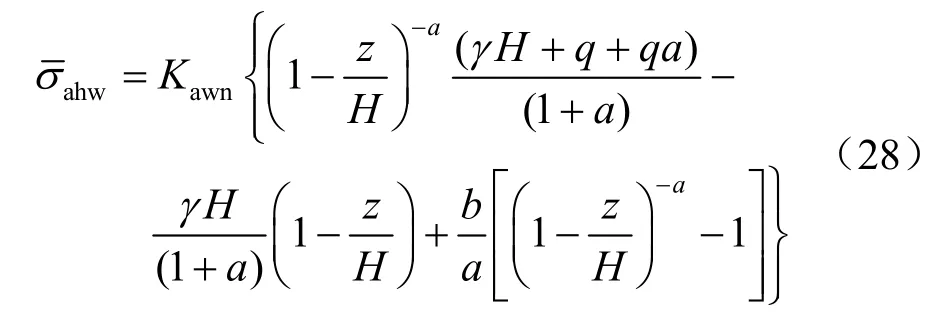
式中：a为内摩擦角的影响；b为黏聚力的影响。

3.4 基于统一表达式下的被动土压力合力及其作用点高度公式

根据式（28）可推出水平主动土压力合力为

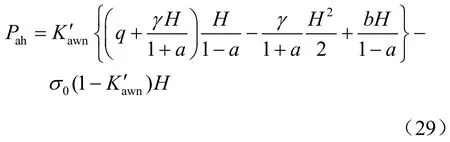
挡土墙总压力为

倾覆力矩为

合力作用点高度可求得

本文给出了分别基于应力状态法和水平静力法两种方法的统一表达式被动土压力解，区别主要体现在参数a、b 的取值上，其中a 代表土的内摩擦角的影响；b 表示黏聚力的影响。当b 取为0时即c=0 kPa，本文给出的公式便可退化为砂土。

从式（29）～（32）可知，a 的范围在0～1。若a ＜ 0，求出来的应力分布为上大下小，与实际不符；a ＞ 1，则所求出来的合力为无穷大，无法求出合力，这与实际也不相符。这条也是衡量土拱理论对求解被动土压力适用范围的一条准则，当a 超过上述范围，则无法应用。

4 算例研究

4.1 砂性土土压力计算研究

选用文献[2]的试验结果，土工试验参数为q=0 kN/m，γ=15.64 kN/m3，c=0 kPa，δ=2/3φ，φ=34.2°，挡土墙高H=1 m。

图5 和表1 表明，静力平衡法得到的被动土压力分布与侯键法求得的结果在0.95H 高度范围内较为相似，因为二者的本质都是基于土楔形体静力平衡，区别在于两者采用的滑裂面不同。应力状态法较前面这种方法计算结果小一些。表1为4 种方法总压力及其作用点高度计算结果，应力状态法给出的结果与Rankine 相近。应用文献[10]的方法无法求得合力大小，其原因是其系数a ＞ 1，其合力趋于无穷大。

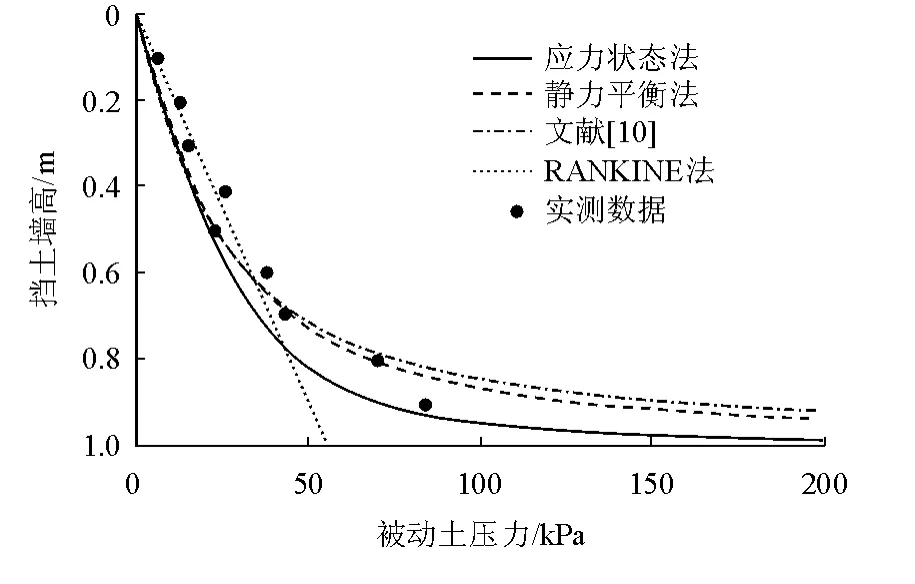
图5 不同方法计算结果对比Fig.5 Comparison among experimental results and different results by different theory

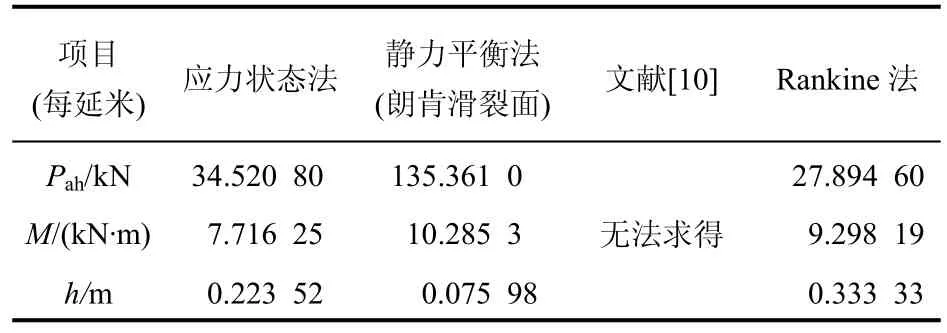
表1 各种方法计算结果对比Table 1 Comparison with results of active pressure behind retaining wall

4.2 黏性土土压力计算研究

图6 的算例条件为：挡土墙高H=1 m，超载q=0 kN/m，黏聚力c=20 kPa,内摩擦角φ=30°，墙土摩擦角δ=0.8，φ=24°，土体重度γ=18 kN/m3。由图可见，黏性土填料下的挡土墙被动土压力分布也呈现上小下大的指数型形状，并且静力平衡法求得结果较应力状态法求得的结果更大。

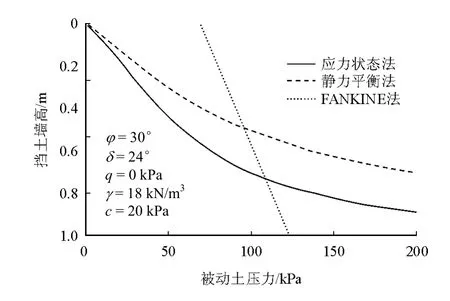
图6 黏性土被动土压力计算比较Fig.6 Comparison with results of passive earth pressures behind retaining wall of cohesive clay

图7 的算例条件除了墙土摩擦角为一变值外，其他条件均与图6 的条件一致。由图可见，从作用点高度来看，随着δ/φ 的增大，土拱效应逐渐增强，下部土体应力比重越来越大，土体合力点逐渐下降。采用静力平衡法求得的土压力作用点高度随着δ/φ 的增大，作用点高度逐渐趋于0，其原因就在于a 值趋于1。

图7 黏性土被动土压力作用点高度计算比较Fig.7 Comparison with heights of resultant passive earth pressure behind retaining wall of cohesive clay

5 结 论

（1）基于圆弧土拱及朗肯滑裂面，本文给出了考虑土拱效应的被动土压力侧向土压力系数，分别基于滑裂面处应力状态及土楔形体静力平衡给出了挡土墙竖向平均应力分布公式。

（2）得到了挡土墙被动土压力膜分布规律及土压力合力，倾覆力矩及作用点高度计算公式，不管是黏性土，还是砂土，挡土墙被动土压力分布都呈上小下大的指数型形状。

（3）随着δ/φ 的增大，土拱效应逐渐增大，土体下部应力逐渐增大，挡土墙作用点高度逐步下降。

（4）判断土拱理论求解挡土墙被动土压力的标准为：0 ＜ a ＜ 1。若a ＞ 1，则所求得挡土墙被动土压力合力为无穷大，而作用点高度趋于0。

[1]FANG Yung-show,HO Ying-chieh,CHEN Tsang-jiang.Passive earth pressure with critical state concept[J].Journal of Geotechnical and Geoenvironmental Engineering,2002,128(8):651-659.

[2]陈页开.挡土墙上土压力的试验研究与数值分析[D].杭州:浙江大学,2001.

[3]MATSUO M.,KENMOCHI S,YAGI H.Experimental study on earth pressure of retaining wall by field tests[J].Soils and Foundations,1978,18(3):27-41.

[4]林宇亮,杨果林,黄向京.膜挡墙后黏性土被动土压力的薄层微元法[J].公路交通科技,2011,28(3):12-19.LIN Yu-liang,YANG Guo-lin,HUANG Xiang-jing.Thin-layer micro-element method for computing passive earth pressure of back filled cohesive soil on retaining wall[J].Journal of Highway and Transportation Research and Development,2011,28(3):12-19.

[5]王元战,李珊珊,李新国.挡土墙被动土压力分布与被动侧压力系数[J].中国港湾建设,2006,144(4):9-12.WANG Yuan-zhan,LI Shan-shan,LI Xin-guo.Passiveearth pressure on a retaining wall and lateral coefficient ofpassive earth pressure[J].China Harbour Engineering,2006,144(4):9-12.

[6]TERZAGHI K.Theoretical soil mechanics[M].New York：John Wiley and Sons,1943:66-76.

[7]彭述权,周健,樊玲,等.考虑土拱效应刚性挡墙土压力研究[J].岩土力学,2008,29(10):2701-2707.PENG Shu-quan,ZHOU Jian,FAN Ling,et al.Research on earth pressure of rigid retaining wall considering soil arching[J].Rock and Soil Mechanics,2008,29(10):2701-2707.

[8]李永刚.挡土墙被动土压力研究[J].岩土力学,2003,24(2):273-276.LIYong-gang.Study on passive earth pressure of retaining wall[J].Rock and Soil Mechanics,2003,24(2):273-276.

[9]吴明,彭建兵,徐平,等.考虑土拱效应的挡墙后土压力研究[J].工程力学,2011,28(11):85-95.WU Ming,PENG Jian-bing,XU Ping,et al.Study onearth pressure against rigid retaining walls considering soil arching effects[J].Engineering Mechanics,2011,28(11):85-95.

[10]侯键,夏唐代,孔祥冰,等.基于土拱效应原理求解挡土墙被动土压力[J].岩土力学,2012,33(10):2296-3000.HOU Jian,XIA Tang-dai,KONG Xiang-bing,et al.Passive earth pressure on retaining walls calculated by principle of soil arching effect[J].Rock and Soil Mechanics,2012,33(10):2296-3000.

[11]王立国,王志凯.考虑土拱效应的挡土墙被动土压力分析[J].水利与建筑工程学报,2010,8(4):146-149.WANG Li-guo,WANG Zhi-kai.Analysis on passive earth pressure for retaining walls considering soil arching[J].Journal of Water Resources and Architectural Engineering,2010,8(4):146-149.

[12]QUINLAN J F.Discussion of the arch in soil arching[J].Journal of Geotechnical Engineering,1987,113(3):272-274.

[13]PAIK K H，SALGADO R.Estimation of active earth pressure against rigid retaining walls considering arching effects[J].Geotechnique,2003,53(7):643-653.

[14]涂兵雄,贾金青.考虑土拱效应的黏性填土挡土墙主动土压力研究[J].岩石力学与工程学报,2012,31(5):1064-1070.TU Bing-xiong,JIA Jin-qing.Research on active earth pressure behind rigid retaining wall from clayey backfill considering soil arching effects[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(5):1064-1070.