基于最大熵原理的黄土丘陵区地质灾害规模频率分布研究

邱海军 ，崔 鹏，曹明明，刘 闻，高 宇，王彦民

（1.西北大学 城市与环境学院，西安 710127；2.中国科学院水利部成都山地灾害与环境研究所，成都 610041；3.陕西理工学院 化学与环境科学学院，陕西 汉中 723001）

1 引 言

崩塌、滑坡和不稳定斜坡等地质灾害的规模频率分布曲线对于区域地质灾害宏观表征和定量刻画具有重要的作用。利用这个曲线，可以求解任一规模地质灾害的发生概率，找出规模差异巨大的地质灾害之间所存在的分布规律[1]。国内外的很多学者通过对全球各地区地质灾害规模频率分析后发现：随着崩塌、滑坡和不稳定斜坡面积和体积的增大，它们的数量急剧的减少，并且这种数量关系符合幂律。进一步的研究还发现，当它们的规模较小时，在双对数曲线上规模频率会出现偏转效应，并对造成这种现象的原因进行了讨论[2-6]。另外还有很多学者试图通过分布曲线对规模频率进行拟合。Malamud 等[7]分析了加利福尼亚、意大利中部和危地马拉3个具有良好编目的滑坡数据库，发现滑坡面积概率函数很好地符合截断反伽马（truncated inverse gamma）分布；Stark 等[3]分析了新西兰和台湾的3个滑坡数据库发现，滑坡面积的概率密度函数很好地符合Double Pareto 概率分布；许强[8]、姚令侃[9]、戴福初[10]等对规模频率的幂指数关系进行了探索性研究。

目前在规模频率分布曲线的研究中，当规模较小时，曲线偏转严重，拟合效果很不理想。而用分布曲线拟合时涉及参数又太多，难以确定，一定程度上限制了其应用。最为重要的是这些曲线拟合在理论上缺少必要的支持和证明。

地震现象是复杂的，但人类很早就知道，震级愈大，则发生的次数愈少。并总结出震级Ms和大于震级Ms出现的地震频数N 之间存在著名的古登堡-里查德（Gutenberg-Richter）关系[11]：Log N(＞Ms)=a-bM。这也是地震自组织临界性（Self-organized Criticality，SOC）的体现[9]。与之类似，崩塌、滑坡和不稳定斜坡的形成和发生是在一系列随机性地震、降雨、融雪等自然因素和修路、植被破坏等人为因素的影响下产生的结果[6]。那么这些地质灾害的频率分布是否也遵从着这样简捷的关系呢？如何通过简单地变换使相关参数也符合这种关系呢？这是本文要回答的两个最基本的问题。

黄土高原是黄土崩塌、滑坡和不稳定斜坡等地质灾害的易发区，因这些地质灾害危害大、分布广，成为近年研究热点问题[12-14]。过去传统方法主要从物质组成、地质构造、地形地貌、降雨条件及人为活动等内外因因素进行研究[15-16]，研究内容主要集中于区域地质灾害的易发性、危险性和风险方面[17-19]。本文选择基础的规模参数，进行规模频率分布特征的分析。基于最大熵原理试图从理论上证明基础规模参数的频率分布符合最简单指数分布，并给出拟合方程。这种简单的规模频率分布曲线，对于地质灾害的预测有重要的意义。

2 研究区概况

延安市宝塔区位于陕西北部（见图1），陕北黄土高原中部丘陵沟壑区，属华北陆台鄂尔多斯台地的一部分。介 于 36°11′～37°02′N,109°14′～110°07′E，南北长96 km，东西宽76 km，面积为3 556 km2。北部属半干旱地区，南部属半湿润地区。延安市宝塔区黄土堆积厚度大，结构疏松，水土流失严重，沟壑纵横地形破碎，是我国地质环境极为脆弱的地区之一，特殊的自然地理地质环境以及黄土独特的力学特征（垂直节理发育、湿陷性、结构松散、大孔隙等）导致滑坡、崩塌、泥石流等地质灾害多发[20]。据统计，在黄土高原地区，黄土滑坡发育的密度可以高达6个/km2，每年发生滑坡可以高达数百个[21]。

图1 陕西省延安市宝塔区位置与地质灾害分布图Fig.1 Distribution map of landslide in Baota district

3 数据来源和研究方法

3.1 数据来源

本文主要数据来源有二：一是参考文献[22]的调查结果；二是进行地质灾害详细调查，通过对遥感图像进行正射校正、图像融合、图像增强处理和图像镶嵌与裁剪以及配合大量的野外调查，特别是小比例尺的地质灾害详查完成解译。通过遥感解译数据与地质灾害详查数据相结合，对宝塔区崩塌、滑坡和不稳定斜坡的位置、数量、分布、规模等有了全面的掌握。其中滑坡点291 处，崩塌点51 处，不稳定斜坡52 处（如图1 所示）。

3.2 研究方法

3.2.1 最大熵原理[23]

Shannon 最早用熵来定量地描述一个随机事件的不确定性或信息量[24]：

式中：H 称为信息熵；Pi为随机事件出现的概率；C为常数。从式（1）可知，在给定的条件下，存在一个使H 取极大值的分布，称为最可几分布[25]。此时系统熵值最大，这就是最大熵原理（principle of maximum entropy，POME）。

设随机变量xi(i=1,2,…,n)其相应的概率为Pi，则

为寻求在约束条件式（3）、（4）下熵极大时的分布，引入未定乘子α 和βk,构造一个新函数：

利用不等式ln x ≤x-1，上式可变为

若H 取极大值，则上式必须取等号，此时要求pi满足下式：

由式（3）、（7）可得

若令Z=eα，则

式中：Z 称为配分函数。

将式（9）代入式（7）可得

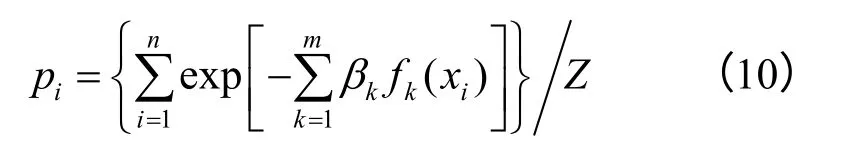
为求得βk，将式（10）代回约束方程式（3），可得

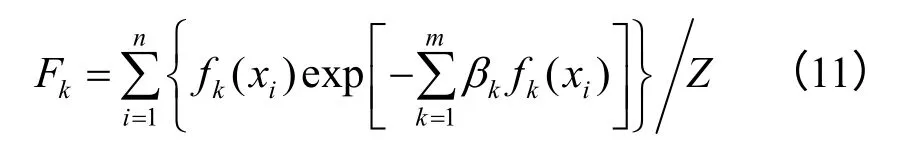
式中 Fk和 fk(xi)为已知值，通过求解方程即可求出熵极大时的pi值。

3.2.2 崩塌、滑坡和不稳定斜坡灾害最大熵原理的导出[23]

熵为系统无序程度的度量，在平衡态系统的状态最混乱、最无序[15]，表明熵已达到最大值。崩塌、滑坡和不稳定斜坡在一系列随机因素的作用下以最无序的方式在区域上发生，意味着它们的熵达到了极大值。基于这样的事实和假设，进行如下的推导。

首先，设M为崩塌、滑坡和不稳定斜坡长、宽和厚等参数，M0为崩塌、滑坡和不稳定斜坡长、宽和厚等参数下限，为崩塌、滑坡和不稳定斜坡平均长、宽和厚等参数，N为大于或等于某一长、宽和厚的崩塌、滑坡和不稳定斜坡个数。由此式（2）变为，其配分函数Z=[exp(-βM)]/β。代入式（11），可得

可见，崩塌、滑坡和不稳定斜坡长、宽和厚等规模参数是一种指数分布。对式（13）两边取对数，可变为

可得

这与地震学中著名的古登堡-里查德（Gutenberg-Richter）定律形式一致。如前所述，滑坡面积和体积参数是长、宽和厚等参数的平方级和立方级。那么当对面积和体积取算术平方根和立方根后，它们的规模-频率分布也应该是负指数分布，即

其面积规模频率分布公式为

其体积规模频率分布公式为

为了验证上述推导结果的正确性，本文以宝塔区崩塌、滑坡和不稳定斜坡为例进行检验。

4 结果与分析

4.1 宝塔区地质灾害规模分布分析

根据地质灾害详细编录数据库分析可得，宝塔区滑坡的平均长度为168 m，平均宽度为256 m，平均厚度为9 m。根据文献[26-27]对滑坡的分类（如表1 所示）。

为了进一步分析不同体积规模上地质灾害分布特征，本文首先按照国土资源部关于崩塌和滑坡等级划分的方法，引入地质灾害规模等级指数：

式中：E为地质灾害规模等级指数；V为地质灾害体积。

经过计算，宝塔区滑坡灾害规模等级介于[3.56，6.88]，崩塌灾害规模等级介于[2.50，5.73]，不稳定斜坡灾害规模等级介于[3.80，6.78]。

对规模等级指数E 进行直方图和累积频率分布分析（见图2），可知：滑坡规模等级指数主要集中于(5.5，6]级，其次为（5，5.5]级；崩塌规模等级指数主要集中于(4，4.5]级，其次为（3.5，4]级；不稳定斜坡规模等级指数主要集中于(5，5.5]级，其次为（5.5，6]级。

表2为宝塔区地质灾害个数，面积和体积分布表，分析可得，大型地质灾害在控制滑坡、崩塌和不稳定斜坡总面积和总体积中起着重要的作用。1个最大的滑坡、崩塌和不稳定斜坡所占的面积百分比分别是其个数百分比的9.50、16.03 和5.21 倍；1个最大的滑坡、崩塌和不稳定斜坡所占的体积百分比分别是其个数百分比的13.82、10.85 和9.01 倍。而最大的5个滑坡、崩塌和不稳定斜坡所占的面积百分比分别是其个数百分比的6.02、6.23 和3.22 倍；最大的5个滑坡、崩塌和不稳定斜坡所占的体积百分比分别是其个数百分比的9.42、6.36 和4.76 倍。

图2 等级指数分布图Fig.2 Distribution map of grade index

4.2 基于最大灾害熵原理的区域地质灾害规模频率分布

4.2.1 区域地质灾害长、宽和厚的规模频率分布

根据最大灾害熵原理导出结果可知崩塌、滑坡和不稳定斜坡长、宽和厚等规模参数是一种指数分布，为了进一步检验其正确性，本文以黄土丘陵区宝塔区的291 处滑坡、51 处崩塌和52 处不稳定斜坡为例进行验证。其中长、宽和厚在半对数坐标系下呈现负指数分布规律（如图3～5 所示）。

图3～5 分别显示了半对数坐标系中崩塌、滑坡和不稳定斜坡长、宽和厚与累计频率的之间的关系，可见其确实呈现指数分布。采用最小二乘法进行曲线拟合，得到最佳拟合方程，并且决定系数R2＞0.9，P＜0.05。

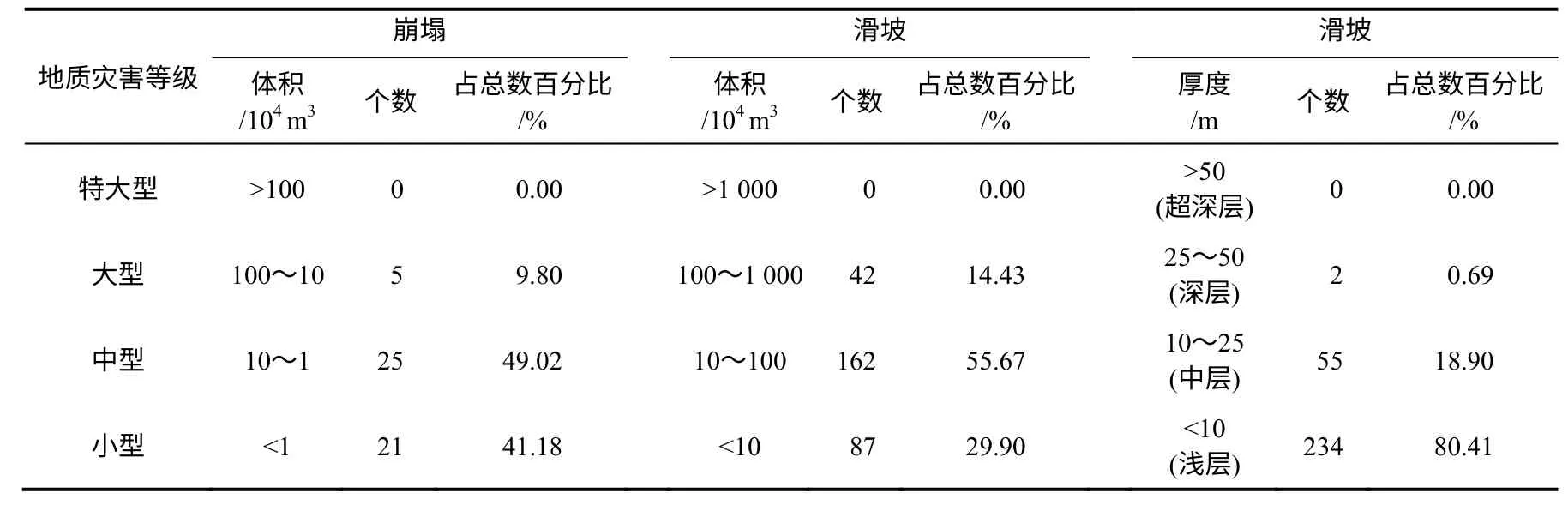
表1 崩塌和滑坡等级划分及其宝塔区分布状况表Table 1 Grading distribution and division of landslide and collapse

图3 滑坡、崩塌和不稳定斜坡的长与频率关系图Fig.3 Relationships between length and frequency of landslide,collapse and instability slope

图4 滑坡、崩塌和不稳定斜坡的宽与频率的关系图Fig.4 Relationships between width and frequency of landslide,collapse and instability slope

表2 宝塔区地质灾害个数、面积和体积分布表Table 2 Distritution of number,area and volume of Geological disasters

图5 滑坡、崩塌和不稳定斜坡的厚与频率的关系图Fig.5 Relationships between thickness and frequency of landslide,collapse and instability slope

其中，滑坡长与累计频率关系最佳拟合方程为

崩塌长与累计频率关系最佳拟合方程为

不稳定斜坡长与累计频率关系最佳拟合方程为

滑坡宽与累计频率关系最佳拟合方程为

崩塌宽与累计频率关系最佳拟合方程为

不稳定斜坡宽与累计频率关系最佳拟合方程为

滑坡厚与频率关系最佳拟合方程为

崩塌厚与累计频率关系最佳拟合方程为

不稳定斜坡厚与累计频率关系最佳拟合方程为

由式（19）～（27）可以推算累计频率为25%、50%和75%时地质灾害长、宽和厚参数的值，见表3。

表3 不同累计频率下地质灾害长、宽和厚规模参数值Table 3 Values of length,width and thickness of geological disasters in different cumulative frequencies

4.2.2 区域地质灾害面积和体积的规模频率分布

对于崩塌、滑坡和不稳定斜坡面积与体积规模，其实质是长、宽和厚等参数的平方级和立方级，因此，对于其规模频率分布求解的一个简单的方法是对面积和体积开算术平方根和立方根后再用指数分布对其拟合。结果如图6、7 所示。

图6、7 显示了半对数坐标系中崩塌、滑坡和不稳定斜坡面积与体积的算术平方根和立方根与累计频率的之间的关系，可见其确实呈现一种负指数分布。采用最小二乘法进行曲线拟合，得到最佳拟合方程，并且决定系数R2＞0.9，P＜0.05。

图6 滑坡、崩塌和不稳定斜坡的面积算术平方根和频率关系图Fig.6 Relationships between square root of area and frequency of landslide,collapse and instability slope

图7 滑坡、崩塌和不稳定斜坡的体积立方根和频率关系图Fig.7 Relationships between cube root of volume and frequency of landslide,collapse and instability slope

滑坡面积与累计频率关系最佳拟合方程为

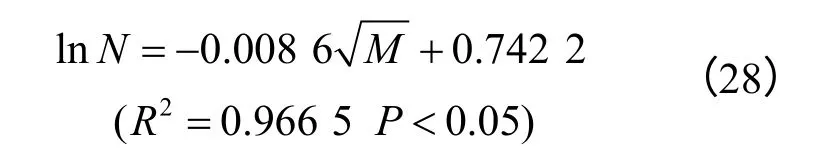
崩塌面积与累计频率关系最佳拟合方程为

不稳定斜坡面积与累计频率关系最佳拟合方程为

滑坡体积与累计频率关系最佳拟合方程为

崩塌体积与累计频率关系最佳拟合方程为

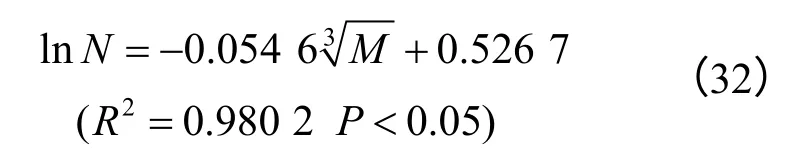
不稳定斜坡体积与累计频率关系最佳拟合方程为

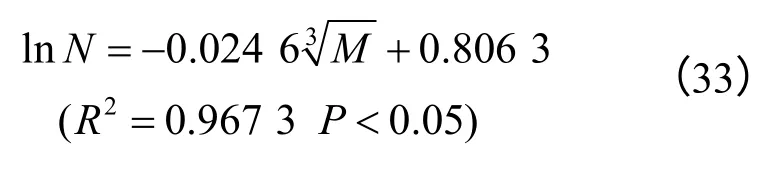
由式（28）～（33）可以推算累计频率为25%、50%和75%时地质灾害面积和体积参数的值，见表4。

表4 不同累计频率下地质灾害面积和体积规模参数值Table 4 Values of area and volume of geological disasters in different cumulative frequencies

由此可见，地质灾害长、宽、厚参数规模频率分布可以用负指数模型来表示，相关面积和体积参数规模频率分布经变换可以转换为指数关系。更为重要的是用指数关系或对面积和体积规模参数开算术平方根和立方根后的指数关系拟合的规模频率曲线，在规模较小时不会产生以往研究者所提出的产生偏转效应。不难发现，已往的研究之所以没有发现地质灾害规模频率的指数分布形式，在于其研究集中于面积或体积的频率分布，而面积和体积是长、宽、厚参数的平方和立方级，这就不自觉地加深了其规模频率分布曲线的弯曲程度，加大了拟合难度，这样偏转效应就会自然产生。本文对面积和体积频率分布曲线经过简单地取其算术平方根和立方根就可以转化为指数分布形式，这种简捷而有效分布形式对于预测任一规模滑坡发生频率具有重要意义。

5 结论与讨论

（1）宝塔区地质灾害以中型滑坡和中型崩塌为主，但大型地质灾害对总面积和总体积有着重要的控制作用。

（2）宝塔区滑坡灾害规模等级介于[3.56，6.88]，崩塌灾害规模等级介于[2.50，5.73]，不稳定斜坡灾害规模等级介于[3.80，6.78]。其中滑坡规模等级指数E 主要集中于(5.5，6]级，其次为（5，5.5]级；崩塌规模等级指数E 主要集中于（4，4.5]级，其次为（3.5，4]级；不稳定斜坡规模等级指数E 主要集中于(5，5.5]级，其次为（5.5，6]级。

（3）与古登堡-里查德（Gutenberg-Richter）定律类似，崩塌、滑坡和不稳定斜坡的长、宽、厚规模频率分布符合更简单的指数关系，见式（15），且用指数关系拟合的规模频率曲线不会产生偏转效应。在半对数坐标系中采用最小二乘法进行曲线拟合得到崩塌、滑坡和不稳定斜坡长、宽、厚与累计频率的之间的关系，可见其确实呈现一种负指数分布，并且拟合效果良好（R2＞0.9，P＜0.05）。

（4）崩塌、滑坡和不稳定斜坡面积与体积规模，其实质是长、宽、厚等参数的平方级和立方级，对于其规模频率分布求解的一个简单的方法是对面积和体积开算术平方根和立方根后再用指数分布对其拟合。即面积频率关系见式（16），体积频率关系见式（17）。试验表明，其确实呈现一种负指数分布，并且拟合效果良好。

（5）文中所推导的规模频率分布曲线方程是一种简单的负指数分布，简捷而有效，便于推广应用。这对于预测任一规模滑坡发生频率具有重要意义。

总之，科学研究对规律的探寻很大程度上表现为探索变化中的不变性和不变中的可比性，科学思考的目的在于寻找特殊中的一般和变化中的永恒，而这种不变性对于认识世界本质和揭示事物规律具有重要的价值。地质灾害的规模频率分布正是空间上大量分布的地质灾害点所具有的不变性和遵循的宏观规律。上述结果再次证明，区域地质灾害的统一性不仅在于它们微观构成的单一性，而且表现在宏观上所遵从的某些普遍的规律。一些看起来似乎是毫无关联的地质灾害事件，实际上都在遵从着某种既定的规律，这也反映了世界的统一性和普适性。

[1]GUTHRIE R H,EVANS S G.Magnitude and frequency of landslides triggered by a storm event,Loughborough Inlet,British Columbia[J].Natural Hazards and Earth System Science,2004,4(3):475－483.

[2]PELLETIER J D,MALAMUD B D,BLODGETT T,et al.Scale-invariance of soil moisture variability and its implications for the frequency-size distribution of landslides[J].Engineering Geology,1997,48(3):255－268.

[3]STARK C P,HOVIUS N.The characterization of landslide size distributions[J].Geophysical Research Letters,2001,28(6):1091—1094.

[4]GUZZETTI F,MALAMUD B D,TURCOTTE D L,et al.Power-law correlations of landslide areas in central Italy[J].Earth and Planetary Science Letters,2002,195(3):169－183.

[5]BRARDINONI F,CHURCH M.Representing the landslide magnitude-frequency relation:Capilano River basin,British Columbia[J].Earth Surface Processes and Landforms,2004,29(1):115－124.

[6]VAN DEN EECKHAUT M,POESEN J,GOVERS G,et al.Characteristics of the size distribution of recent and historical landslides in a populated hilly region[J].Earth and Planetary Science Letters,2007,256(3):588－603.

[7]MALAMUD B D,TURCOTTE D L,GUZZETTI F,et al.Landslide inventories and their statistical properties[J].Earth Surface Processes and Landforms,2004,29(6):687－711.

[8]许强，黄润秋.地质灾害发生频率的幂律规则[J].成都理工学院学报,1997,24:91－96.XU Qiang,HUANG Run-qiu,Power law between volume and frequency of geological hazards[J].Journal of Chengdu University of Technology,1997,24:91－96.

[9]姚令侃，黄艺丹，杨庆华.地震触发崩塌滑坡自组织临界性研究[J].四川大学学报:工程科学版,2010,42(5):33－43.YAO Ling-kan,HUANG Yi-dan,YANG Qing-hua.The self-organized criticality of landslids triggered by earthquake[J].Journal of Sichuan University(Engineering Science Edition),2010,42(5):33－43.

[10]DAU F C,LEE C F.Frequency-volume relation and prediction of rainfall-induced landslides[J].Engineering Geology,2001,59(3):253－266.

[11]BAK P,TANG C.Earthquakes as a self‐organized critical phenomenon[J].Journal of Geophysical Research:Solid Earth,1989,94(11):15635－15637.

[12]许领，戴福初，闵弘.黄土滑坡研究现状与设想[J].地球科学进展,2008,23(3):236－242.XU Ling,DAI Fu-chu,MIN Hong.Research progress and some thoughts on loess landslides[J].Advances in Earth Science,2008,23(3):236－242.

[13]叶万军，董西好，杨更社，等.倾倒型黄土崩塌稳定性判据及其影响范围研究[J].岩土力学,2013,34(增刊2):242－246.YE Wan-jun,DONG Xi-hao,YANG Geng-she,et al.Stability criterion and influencing zone of loess collapse with toppling style[J].Rock and Soil Mechanics,2013,34(Supp.2):242－246.

[14]周跃峰，谭国焕，甄伟文，等.入渗诱发黄土滑坡的力学机制[J].岩土力学,2013,34(11):3173－3179.ZHOU Yue-feng,TAN Guo-huan,YAN Wei-wen,et al.Mechanism of infiltration-induced loess landslides[J].Rock and Soil Mechanics,2013,34(11):3173－3179.

[15]徐张建，林在贯，张茂省.中国黄土与黄土滑坡[J].岩石力学与工程学报,2007,26(7):1297－1312.XU Zhang-jian,LIN Zai-guan,ZHANG Mao-sheng.Loess in China and loess landslides[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(7):1297－1312.

[16]念秦,倬元.黄土滑坡灾害研究[M].兰州:兰州大学出版社,2005.

[17]张春山,何淑军,辛鹏,等.陕西省宝鸡市渭滨区地质灾害风险评价[J].地质通报,2009,28(8):1053－1063.ZHANG Chun-shan,HE Shu-jun,XIN Peng,et al.Risk evaluation of geological hazards in Weibin District,Baoji City,Shaanxi Province,China[J].Geological Bulletin of China,2009,28(8):1053－1063.

[18]唐亚明，张茂省，薛强.陕西延安市虎头峁滑坡社会风险评价[J].地质通报,2009,27(11):1782－1786.TANG Ya-ming,ZHANG Mao-sheng,XUE Qiang.Social risk assessments of the Hutoumao landslide in Xi’an City,Shaanxi,China[J].Geological Bulletin of China,2008,27(11):1782－1786.

[19]韩金良，燕军军，孙炜锋，等.陕西省宝鸡市陈仓区吴家沟滑坡风险评价[J].地质通报,2009,28(8):1118－1126.HAN Jin-liang,YAN Jun-jun,SUN Wei-feng,et al.Risk assessment of Wujiagou landslide in Chencang District,Baoji City,Shaanxi Province,China[J].Geological Bulletin of China,2009,28(8):1118－1126

[20]庄建琦，彭建兵，张利勇.不同降雨条件下黄土高原浅层滑坡危险性预测评价[J].吉林大学学报(地球科学版),2013,43(3):867－876.ZHUANG Jian-qi,PENG Jian-bing,ZHANG Li-yong.Risk assessment and prediction of the shallow landslide at different precipitation in loess plateau[J].Journal of Jilin University(Earth Science Edition),2013,43(3):867－876.

[21]雷祥义.黄土高原地质灾害与人类活动[M].北京:地质出版社,2001.

[22]张茂省.延安宝塔区滑坡崩塌地质灾害[M].北京:地质出版社,2008.

[23]冯利华，张萍.基于最大熵原理的台风统计预报[J].海洋科学,2003,27(3):47－51.FENG Li-hua,ZHANG Ping.Statistical forecast of typhoon based on maximum entropy principle[J].Marine Sciences,2003,27(3):47－51.

[24]SHANNON C E.A mathematical theory of of soil 6－坡870 ng.ive ese 2):E.em on 9.of nite,2:ton 70,析of[J].communication[J].ACM SIGMOBILE Mobile Computing and Communications Review,2001,5(1):3－55.

[25]张学文，马力.熵气象学[M].北京:气象出版社,1992.

[26]国土资源部.县(市)地质灾害调查与区划基本要求(修改稿)实施细则[S].北京:国土资源部,2006.

[27]国土资源部.地质灾害危险性评估技术要求[S].北京:国土资源部,2004.