基于无限边坡算法的降雨型滑坡预警系统的模型试验研究

王 俊，黄润秋，聂 闻, ，苏小鹏

（1.重庆大学 煤矿灾害动力学与控制国家重点实验室，重庆 400044；2.成都理工大学 地质灾害防治与地质环境保护国家重点实验室，成都 610059）

1 引 言

降雨型滑坡是世界上最重要的地质灾害之一[1－5]。随着信息技术的发展，滑坡早期预警系统由于其较低的环境和经济成本，已经逐渐进入人们的视野。特别是在一些大型滑坡案例中，由于传统的防治手段例如锚杆、挡土墙无法实施，早期预警系统成为了最佳选择。Medina-Cetina 等[6]定义早期预警系统是一种减少或避免外界威胁人类财产安全的工具。通常，一个有效的早期预警系统应该包括4个部分[7]：①监测，包括数据获取，传输和设备维护；②分析与预测，包括如何设定阈值，专家判断，预测方法等；③警告，预警信息的发布；④响应，确保人们明白和如何应对警告。然而，上述的早期预警系统并不容易实现，尤其是第③、④部分。目前，大部分的预警系统的目标仍然是第①部分（监测与获取数据）和第②部分（分析与预测滑坡），对此可以称为技术性预警系统。大体上，降雨型滑坡预警系统分为两类：由于经验降雨阈值的发展[8]，针对特定地区的基于累积降雨指标的预警系统被首先建立[9－10]并取得了不少成果。该类预警系统具有构造简便等特点，但由于缺乏物理依据，没有具体考虑滑坡体的地质环境及条件，准确性仍然不高，只能用于区域性的大致预警。另一方面，针对具体单个滑坡失稳的预警系统，由于其构造机制较为复杂，目前仍然比较少见。例如Thiebes 等[11]最近在奥地利阿尔卑斯山发展了一个基于安全因子极限平衡算法的预警系统。不过其需要的水文指标、地质信息较多导致了其预警系统过于复杂。本文通过建立一种比较简单的基于无限边坡算法的技术性预警系统，展示预警平台如何耦合滑坡稳定性分析模型进行滑坡阈值估算，如何运用网络传输技术与专家交流。整个预警系统重点关注预报滑坡发生破坏的时间，通过在实验室构建降雨型滑坡模型试验系统，选择初始含水较高的场景即滑坡失稳前有较多的前期降雨模拟滑坡失稳的场景。最后对比模型试验与预警系统预测结果，并评估其效用。

2 预警系统的构建

2.1 预警思路

整个技术性预警系统思路如图1 所示，首先，天气预报可以提前一两天以较低精度获得预估降雨状态，即牺牲预警准确度换取预警时间（中短期预警）；而实时监测数据会大幅度提高预警准确度，但预警时间较短。当监测降雨信息获得后，系统将检查当时含水状态，包括含水率和地下水位线，如果没有达到系统开始计算的阈值，则保持监控。一旦超过预存值，系统开始估算入渗量，进而推算出可能增加的地下水位线，再根据无限边坡模型计算出安全因子FOS。如果FOS 超过设定阈值，将通过网页通知服务系统发给专家，专家查看数据信息后进而确定是否发布预警；如果没有超过设定阈值则系统继续监测含水状态。

2.2 预警时间计算原理

该预警系统针对的是比较常见的浅层降雨型滑坡，其地质状况为深部有稳定性较好、渗透较差的基岩或者紧密的土体，而表层土体呈现出长条状，其厚度低于长度，并且坡顶不容易形成集水，例如意大利南阿尔卑斯山[12]和新西兰地区的浅层滑坡[13]。这种滑坡可采用无限边坡模型计算稳定性[14]，对于这类无限边坡，通常假定潜在滑动面和地下水位线大致平行于坡面，随着降雨进行，由于表面与内部汇流至坡脚，导致坡脚部分首先失稳破坏，其计算的公式与原理参考图2 和式（1）。

式中：H为滑体厚度；γ为材料密度；β为滑坡坡脚；u为地下水在滑动面产生的孔隙水压力；φ′为饱和内摩擦角；c′为饱和内聚力；FOS为安全因子。

降雨入渗土体时，表层先产生湿润前锋。然后前锋下移，在透水性较低或不透水层开始产生地下水位线。随着地下水位线在滑动面附近的孔隙水压力增加，土体的有效应力降低，进而降低了土体的抗滑力，导致滑坡失稳。因此，由地下水产生的孔隙水压力是整个预警系统的一个关键因素。地下水位通常受很多其他因素影响，其中最重要的为土的入渗速率[15]。通常较强的降雨会引起较大的入渗速率，但土壤最大入渗能力又限制了降雨最大的入渗速率[16]。本文中入渗速率通过模型试验监测表面径流计算获得（见图3），通过对入渗速率与时间的拟合关系（指数关系）进行积分得到累积入渗与时间的新的指数关系式。然后计算累积入渗量与孔隙水压力的关系（见图4）。再根据累计入渗与孔隙水压力的拟合关系，建立孔隙水压力u 与预警时间t 的一个二次关系。预警系统通过设定的FOS 的值反带入公式中，进行迭代计算，最后找到预警时间的收敛值。需要说明的是预警系统嵌入了不同降雨强度下预警时间的计算公式（考虑到计算公式的拟合系数不同）。针对获取的降雨强度数据，系统会首先计算出一个预警时间，当降雨强度改变时（接收到新的降雨信息），系统会自动转换不同的计算公式，得到新的预警时间，实现一个动态预警。这里仅展示10、35、65 mm/h 共3 种比较典型的小、中、大降雨数据。边坡稳定性分类参考表1[17]，FOS 是1.00或1.25，可被认为是一级或二级预警。

图1 预警思路示意图Fig.1 Warning idea

图2 无限边坡安全因子计算Fig.2 Calculation of safety factor for infinite slope model

图3 入渗率与时间关系Fig.3 Infiltration vs.time

图4 累计入渗与孔隙水压力关系Fig.4 Accumulative infiltration vs.pore water pressure

2.3 信息交流与反馈

该系统一个重要的构成叫做网页进程服务（WPS）[18]，基本原理是运行已经嵌入在服务器上的边坡稳定性算法。在案例中，无限边坡模型[14]被整合入该技术性预警系统，通过量化的降雨预测和实时监测数据，自动计算边坡失稳预警时间。这种算法需要首先输入固定参数和导入变化监测数据，其中固定参数包括几何参数、材料属性及入渗系数；变化的参数包括降雨监测与预测数据、实时监测的地下水位数据（见图5）。当计算预警时间值达到了预先设定的滑坡时间阈值时，另一个重要的数据管理和可视化平台通过网页通知服务（WNS）[19]自动将短信和邮件传送给专家，专家可以通过互联网查询基于网页的可视化监测数据、曲线、在线视频及阈值算法计算结果，最后再决定是否发布预警信息（见图6）。WPS 与WNS 服务均通过VC++编程实现。其中GPRS 模块通过RS232 接口与服务器连接，由微软提供的Serial 类操作串口与GPRS 模块进行通信。

表1 基于安全因子的稳定性分类Table1 Classification of stability based on FOS

图5 预警模型算法Fig.5 Warning algorithm of model

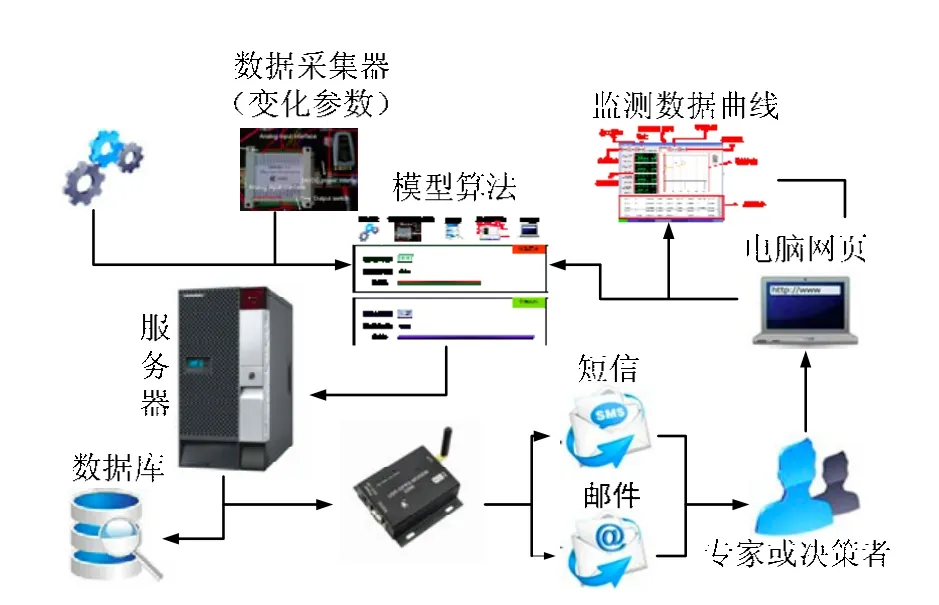
图6 网页通知服务流程图Fig.6 Flowchart of WNS

3 滑坡模型试验

3.1 模型系统

降雨模拟系统主要由水箱、水泵、供水管、阀门、流量计、支撑金属支架和喷头组成。其中HGL-128 型全自动冷热多用泵为模拟降雨装置提供固定压力，最大流量为25 L/min，最大扬程为5 m；玻璃转子流量计的测量范围分别为10～100 和25～250 ml/min，可通过控制流量计流量获得不同的降雨强度。

监测系统包括CYY2 型孔隙水压力传感器，直径为3 cm，高为1.6 cm，测量范围为±10 kPa，输出信号范围为4～20 mA，供电方式为DC24V；PHTS土壤湿度传感器，测量点为3 根钢针，接触面积不到20 mm2，测量范围为0～100%，分辨率为0.1%，准确度为+2%，输出形式为电流4～20 mA，供电方式为DC24V；视频监控系统采用ZION-ipc8000DC1型高清网络摄像头，用于监控滑坡发生及结合量杯监测坡体内部排水速度、地表径流速度等。数据采集卡为CK01L0R-C20 型，采用RS485 接口，传输距离远，稳定性高，软件采用MODBUS-RTU 协议，传输稳定，通用性好，多通道模拟量输入，14bitADC精度，采集0～20 mA 电流。另外，利用VC++自行开发监测软件，可实现同时对多个传感器实际电流值监测、自动换算需要的输出单位、数据变化曲线图、数据记录和输出，并可以随时调节监测时间间隔，如20 s/次。

滑坡物理模型如图7(a)所示，图中，m1、m2、m3为含水率传感器；p1，p2为孔隙水压传感器；s1为土压力计；排水沟1、2 分别测地表排水和内部径流。为了便于观察，斜坡模型采用8 mm 有机透明玻璃制成，并在其表面贴防护膜以减小边界效应。试验材料由河沙按比例混合12%的黏土配成，其粒径分布见图7(b)。共分3 次压土，前两次压土均匀施加5 kg 砝码压力，第3 次施加3 kg 砝码压力。考虑上层土的重力作用，与表层相比，深层土体可认为较紧密且渗透率较低，而表层考虑为较松散的高渗透率材料，可认为表层产生假定潜在滑动面，即是与无限边坡类似的浅层滑坡破坏模式。如图7(a)所示，整个滑面默认为有近似相同的地下水位线。因此，仅监测p2点孔隙水压力，近似替代整个滑面的孔隙水压是合理的，理由为：①滑动面尺寸相对较小，增加孔隙水压力传感器会引起较大的误差；②无限边坡算法通常假定潜在滑动面和地下水位线大致平行于坡面；③滑动面上部孔隙水压力事实上偏小，但考虑滑坡体可靠性问题可计算较大值，即用前段较大的孔隙水压监测值代替整个滑动面的孔隙水压力值（注：实际情况可能是前段先发生破坏[13]）。表层材料的参数如表2 所示。另外排水沟1主要测试地表径流，而排水沟2 测试内部排水。

图7 滑坡模型Fig.7 Physical slope model

3.2 试验方案

降雨强度被认为是影响滑坡失稳时间最重要的因素，所以在整个试验中，共涉及到7 种降雨强度（10、15、25、35、45、55、65 mm/h），持续时长为36 min。每次试验前，对滑坡体均匀透水，排水10 h 固结，尽可能保证每次试验的初始含水状态相同，误差范围在±5%以内。为了缩短滑坡发生的时间，模拟降雨后的再次降雨诱发滑坡失稳，整个试验的整体初始含水状态较高，主要强调短期预警。另外，附加1 次每12 min 改变一次降雨强度的不规则降雨（25、25、65、45、25 mm/h)，且降低初始含水状态，目的是检验变降雨强度不同初始含水状态对预警时间的影响。

表2 第3 层土属性Table 2 Surface soil property of layer 3

3.3 试验结果

图8 分别展示了10、35、65 mm/h 和不规则降雨条件下的模拟场景。本文重点关注第1 次浅层滑坡（有阴影的部分）。图9 分别展示了不同降雨强度下滑坡地表水与地下水的情况。图10、11为不规则降雨条件的含水率与孔隙水压力传感器监测数据。表3 表明了预警系统估计的滑坡破坏时间与真实情况的差别。由于模型几何尺度较小，为了减少预警系统过分敏感性，预警值四舍五入精确到min。

图8 不同降雨条件的模拟场景Fig.8 Slopes of different rainfall intensities

4 试验讨论

4.1 水文特征分析

从图9(a)可以看出，孔隙水压力p1在不同的降雨强度下都有着近似的变化规律。由于p1距离地表及滑动面最远，尽管土壤侵蚀或者浅层发生滑坡，其受到的影响都很小。对比图9(b)，孔隙水压力p2为正值，且降雨强度越大，其增加的速度越快。另外在滑坡发生的时间点附近，其值都体现了先增加后降低的特点（参考图12）[12－13,20－21]。其中降雨10 mm/h 条件下，没有出现上述特征，并且该强度下p2监测值的波动在整个过程中受土体侵蚀的影响较小，这或许是降雨强度较小，滑体比较薄而远离了p2。

对含水率测试而言，如图9(c)中的m1传感器，其位于坡体最顶部，没有上部的径流补充，其大致规律为降雨强度的增加加快了含水率增加的速率。但中等降雨（35、45 mm/hr）比高强度降雨（55、65 mm/h）较早产生了含水率增加现象，推测其原因是由于在高强度降雨下表面侵蚀较严重，而这种侵蚀反过来影响了入渗速率。如图3 所示，在3 min后中等降雨的入渗速率高于高强度降雨入渗速率，这与渗透理论有所不符合[15－16]。需要用基于非达西渗流的应力渗透理论来解释，例如Forchheimer 方程[22]。m2位于m1正下方约20 cm 的位置属于较深，由于密实度的增加，其附近的渗透速率较m1慢。加上上部的水有相当一部分流向了m3，故整个过程中增加的幅度较低。但在降雨强度为10、15、25 mm/h时，含水率增加速率相对较快，推测其原因是这3种情况下顶部侵蚀较小，特别是10 mm/h 完全入渗，导致垂直入渗速率较快，但是否有量化关系仍需要进一步验证。而另一个关键的测试点m3，与m1一样，其大致规律为降雨强度的增加加快了含水率增加的速率。但在7 min 后，45、55 mm/h 含水率增加速率相对65 mm/h 较快，原因是6 min 65 mm/h工况发生了一次滑坡，离m3位置很近。尽管45、55 mm/h 在8 min 后也发生了滑坡，但都在坡脚离m3较远，故影响较小。同样地，与m1相比，6 min前，降雨侵蚀对入渗率的影响并不明显。其实，这主要是因为m3有上部径流的补偿造成的。另外，如图9(f)所示，坡体内部的排水与侵蚀、滑坡的关系并不大，基本上还是可以用典型的排水试验结果，例如Tank 模型来解释[23]。

图9 不同降雨强度下边坡孔隙水压力、含水率、排水变化曲线Fig.9 Pore water pressure and moistures and drainage vs.time under different rainfall intensities

图10 不规则降雨条件下孔隙水压力p1和p2Fig.10 Pore water pressure vs.time under variable rainfall intensities

最后讨论不规则降雨的工况，孔隙水压力数据如图10 所示，对p2而言在两次滑坡发生时间附近都出现了类似图12 的波动。而p1由于深度的影响，降雨增加引起的上升与降雨减少引起的下降都有一

图11 不规则降雨条件下含水率m1、m2、m3Fig.11 Moistures vs.time under variable rainfall intensities

表3 系统预测时间与实际滑坡对比Table 3 Comparison between predication and real landslide

图12 不同降雨强度下滑坡失稳的孔隙水压力关键点p2Fig.12 p2during the failure time under different rainfall intensities

定的滞后。对于图11 中的m1，在24 min 降雨强度突然增加到65 mm/h时，到含水率开始急剧增加的点用时8 min。而对比图9(c)，这个过程需要12 min，这说明前期含水状态对入渗有一定的影响。而36 min 后降低的降雨强度也放缓了含水率增加的速度。同样的现象也发生在m2处，24 min 后的降雨极大的增加了m2的含水率。但它对36 min 后的降雨变小比较敏感，原因需要进一步分析。同样的，m3对于24 min 后65 mm/h 的大降雨也有一定滞后性，不过由于有上部地表径流和内部渗流的补给，所以当降雨强度降低时，没有较明显的减少。

4.2 破坏与预警分析

如表3 所示，在低降雨强度下（10～25 mm/h）预警系统出现的误差较小；而中高降雨强度下（35～65 mm/h）预警误差有所增加。这最主要的原因是，以砂土为主、黏土为辅的材料容易被降雨侵蚀，特别是高强度降雨。降雨的侵蚀改变了坡体几何形状、渗流规律等，最终放大了模型计算的误差。另一个现象是预测误差普遍为负，即预测时间偏短。参考图8，滑动面位置都处于传感器p2的上方，即H 和u 比预测值偏小（见图1），根据式（1）计算FOS结果偏小，导致预警时间变短。需要说明的是除非坡体有明显的滑动面，否则对大部分降雨型滑坡包括较简单的无限边坡模型，都很难准确地界定滑动面的位置。而在预警系统或风险评估中考虑较危险的状况是相对合理的，因为它赢得了更多的撤离时间。

不规则降雨工况是检验变降雨强度不同初始含水状态对预警时间的影响，在本例中，最外层土体初始含水率m1、m3和孔隙水压力p2均低于规则降雨的初始状态。降雨发生后预警系统始终监控初始含水状态，并不进行计算。24 min时，孔隙水压力p2的值达到0 kPa，有产生地下水位的可能。系统开始计算预警时间，当降雨强度由25 mm/h 变化到了65 mm/h，系统自动按照65 mm/h 参数计算预警时间为5 min。因此，考虑初始含水状态和根据降雨变化调整计算结果在预警系统中扮演着非常重要的角色。

5 系统的评价与展望

基于安全因子极限平衡算法的预警系统比基于经验降雨滑坡统计规律的预警模型有更为严密的理论依据，适合于滑动面、几何形状或材料特定的单体滑坡。本研究中的预警系统考虑了地表径流与入渗的关系，累积入渗与地下水位线的关系。由于材料易受降雨侵蚀，上述关系的测量会受到一定影响。加上监测点较少，水文特征评估的准确性也有待提高。但预警系统本身就是资金与准确度矛盾的平衡。本系统另外一个特点就是考虑了初始含水状态对预警时间的影响和降雨变化带来的计算结果更新。预警系统准确性的影响主要来源于滑动面的界定、高强度降雨对土体侵蚀导致土体几何变形等。因此，这是未来预警系统研究需要注意的方向。另外，需要强调的是，本试验没有考虑不同初始含水状态对入渗的影响。由于尺度较小，并没有考虑降雨入渗到产生地下水之间的时间滞后，其可能会对预警时间有所影响。最后，考虑到不同地质条件、几何形状、甚至植被覆盖，对于不同的单体滑坡应采取不同的预警方法。

6 结 论

（1）基于安全因子极限平衡算法的预警系统是可行的，但准确性受到降雨侵蚀、滑动面的确定、初始含水状态的影响。

（2）滑动面附近的地下水位受滑坡失稳的影响比较明显，而附近非饱和土的含水率受到的影响较小。

（3）降雨产生的侵蚀对地表入渗有一定影响，在侵蚀比较严重的情况下，不能简单地用土壤最大入渗能力进行入渗量的计算。

[1]IVERSON R M.Landslide triggering by rain infiltration[J].Water Resources Research,2000,36(7):1897－1910.

[2]HONG Y,ADLER R,HUFFMAN G.Evaluation of the potential of NASA multi-satellite precipitation analysis in global landslide hazard assessment[J].Geophysical Research Letters,33:L22402.doi:10.1029/2006 GRL028010.

[3]高华喜,殷坤龙.降雨与滑坡灾害相关性分析及预警预报阀值之探讨[J].岩土力学,2007,28(5):1055－1060.GAO Hua-xi,YIN Kun-long.Discuss on the correlations between landslides and rainfall and threshold for landslide early-warning and prediction[J].Rock and Soil Mechanics,2007,28(5):1055－1060.

[4]王宇,李晓,张搏,等.降雨作用下滑坡渐进破坏动态演化研究[J].水利学报,2013,44(4):416－425.WANG Yu,LI Xiao,ZHNAG Bo,et al.Dynamic progressive failure evolution research on landslide under precipitation[J].Journal of Hydraulic Engineering,2013,44(4):416－425.

[5]刘礼领,殷坤龙.暴雨型滑坡降水入渗机制分析[J].岩土力学,2008,29(4):1061－1066.LIU Li-ling,YIN Kun-long.Analysis of rainfall infiltration mechanism of rainstorm landslide[J].Rock and Soil Mechanics,2008,29(4):1061－1066.

[6]MEDINA-CETINA Z,NADIM F.Stochastic design of an early warning system.Georisk:Assessment and Management of Risk for Engineered Systems and Geohazards :2008,2(4):223－236.

[7]INTRIERI EMANUELE,GIGLI GIOVANNI,MUGNAI FRANCESCO,et al.Design and implementation of a landslid eearly warning system[J].Engineering Geology,2012,147－148:124－136.

[8]GUZZETTI F,PERUCCACCI S,ROSSI M,et al.The rainfall intensity-duration control of shallow landslides and debris flows:an update[J].Landslides,2008,5(1):3－17.

[9]ALEOTTI P.A warning system for rainfall-induced shallow failures[J].Engineering Geology,2004,73(3):247－265.

[10]BAUM R L,GODT J W.Early warning of rainfall-induced shallow landslides and debris flows in the USA[J].Landslides,2010,7(3),259－272

[11]THIEBES B,BELL R,GLADE T,et al.Integration of a limit-equilibrium model into a landslide early warning system[J].Landslides,2013,5(6):1－17.

[12]MONTRASIO L,VALENTINO R.Experimental analysisand modelling of shallow landslides[J].Landslides,2007,4(3):291－296.

[13]ACHARYA G.Analysing the Interactions between water-induced soil erosion and shallow landslides[D].Christchurch:University of Canterbury,2011.

[14]BIONDI G,CASCONE E,MAGUERI M,et al.Seismic response of saturated cohesionless slopes[J].Soil Dynamics and Earthquake Engineering,2000,20(1－4):209－215.

[15]BROOKS K N,FFOLLIOTT P F,GREGERSEN H M,et al.Hydrology and the Management Of Watersheds.2nd ed[M].Ames,IA.:Iowa State Press,1997.

[16]FOLEY J,SILBURN D.Hydraulic properties of rain impact surface seals on three clay soils—influence of raindrop impact frequency and rainfall intensity during steady state[J].Soil Research,2002,40(7):1069－1083.

[17]MONTGOMERY D R,DIETRICH W E.A physically based model for the topographic control on shallow landsliding[J].Water Resources Research,1994,30(4):1153－1171.

[18]FOERSTER T,STOTER J.Establishing an OGC web processing service for generalization processes[C]//ICA workshop on Generalization and Multiple Representation,2006.[S.l.]:[s.n.],2006.

[19]BRANDT S,KRISTENSEN A.Web push as an internet notification service[C]//W3C Workshop on Push Technology.Boston:[s.n.],1997.

[20]林鸿州,于玉贞,李广信,等.降雨特性对土质边坡失稳的影响[J].岩石力学与工程学报,2009,28(1):198－204.LIN Hong-zhou,YU Yu-zhen,LI Guang-xin,et al.Influence of rainfall characteristics on soil slope failure[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(1):198－204.

[21]MORIWAKI H,INOKUCHI T,HATTANJI T,et al.Failure processes in a full-scale landslide experiment using a rainfall simulator[J].Landslides,2004,1(4):277－288.

[22]EVANS R D.Characterization of non-Darcy multiphase flow in petroleum bearing formation[D].Norman:University of Oklahoma,1994.

[23]ICHIMURA TARO,TANAKA RYOHEI,SUZUKI Daiken,et al.Evluation of hydraulic properties of slope ground based on monitoring data of moisture contents[C]//4th Japan-Taiwan Joint Workshop on Getechnical Hazards from Large Earthquakes and Heary Rainfalls.Sendai,Japan:[s.n.],2010.