An Analysis of Mean Wave Drift Forces of FPSO Systems by Higher-order Boundary Element Method

WANG Ke,ZHANG Zhi-qiang,XU Wang

(State Key Laboratory of Structural Analysis for Industrial Equipment,Department of Engineering Mechanics,Dalian University of Technology,Dalian 116023,China)

An Analysis of Mean Wave Drift Forces of FPSO Systems by Higher-order Boundary Element Method

WANG Ke,ZHANG Zhi-qiang,XU Wang

(State Key Laboratory of Structural Analysis for Industrial Equipment,Department of Engineering Mechanics,Dalian University of Technology,Dalian 116023,China)

Mean wave drift forces and moments are critical for FPSO systems in mooring,riser installation and offloading.In this paper,higher-order boundary element method(HOBEM)is applied and symmetry is considered to calculate the second order hydrodynamic interactions of Schiehallion type FPSO in NorthSea of England.The surge,sway and yaw mean drift forces on FPSO are computed by near-field method based on direct pressure integration.Comparing to conventional method,current algorithm has high accuracy and can converge steadily even for high frequency waves.It is shown that in order to control FPSO safely under severe sea condition,the FPSO systems should change its weathervaning angle to head sea all the time.

FPSO systems； mean wave drift forces and moments； higher-order boundary element method；near field method

1 Introduction

FPSO Systems(Floating Production,Storage and Offloading System)have become a very important equipment of the exploration and extraction of hydrocarbons from the sea-bottom,and are considered the only feasible solution for safe and cost efficient oil and gas production at large depth,especially in areas with severe wave environments.FPSO systems normally are located hundred miles from onshore zone and can not return to harbor like traditional transfer barge.This kind of production units is very prone to the effects of the weather,in particular as a result of their requirement to remain in the same position for several months or permanent in specific area.The designing of FPSO systems should consider two kinds of environmental loads.One is hydrodynamic forces and motions and the other is mean wave drift forces and moments.Hydrodynamic forces and motions are important to assure FPSO systems safely used in severe conditions.The FPSO systems are like a weathervane ship which is turret free to rotate around a vertical riser systems,this head wave working mechanism allows the ship to be aligned with the resultant of the environmental action,minimizing the loads on the mooringlines and also reducing rolling angle of the ship.On the other hand,as one kind of floating platforms,this ship shaped oil production systems will undergo slow motions from their mean position.The slow motions are excited by the slowly varying steady forces from the environment due to the weak restoring forces of the mooring system and the highly tuned low-frequency resonance of the system.It is therefore vital for the design of moorings and riser systems that the magnitudes of the motions are predicted well and that they are kept within acceptable bounds.The slowly varying steady forces are called mean wave drift forces and can be computed from quadratic products of the first-order quantities.It is well known that two different methods are available for computing the wave drift forces:the near-field method based on the direct pressure integration and the far-field method based on the momentumconservation principle.The near-field method(e.g.Ogilvie,1983)gives six degrees of forces but computations are rather complicated because various components must be evaluated.The far-field method(Maruo,1960;Newman,1967)is relatively easy to compute but gives only the total force on ship in horizontal plane with three degree of motions:surge,sway and yaw.

FPSO systems is a very important naval architecture and should be safely maintained at any severe environmental condition,the wave loads prediction of this kind of platform must be as accurate as possible.Based on linear radiation and diffraction theory,hydrodynamic responses of FPSO can be calculated and used to engineering application during initial stage investigation(Liu Yingzhong et al,1986;Faltinsen,1990).In order to improve the numerical precision of second order mean wave drift force,in present paper the first order radiation and diffraction problem are solved by higher-order boundary element method and the symmetry of body geometry is considered,the mean wave drift forces are obtained by near field method for full six individual components.Basic theory and formulations for mean wave drift forces are expressed in section 2;section 3 discusses the result of mean wave drift forces about Schiehallion type FPSO in NorthSea of England.The conclusion of advantage of higher-order boundary element and understanding of mean wave drift forces are drawn in last section.

2 Theory of boundary value problem

The Cartesian coordinate system （x,y, ）z defined in Fig.1 is stationary relative to the undisturbed position of the free surface and body.The origin is located on the free surface with z axis positive upward.The assumption of a potential flow permits the definition of the flow velocity as the gradient of the velocity potential Φ satisfying the Laplace equation

in the fluid domain.The harmonic time dependence allows the definition of a complex velocity potential φ,related to Φ by Fig.1 FPSO sketch

where Re denotes the real part,ω is the frequency of the incident wave and t is time.The ensuing boundary-value problem will be expressed in terms of the complex velocity potential φ,with the understanding that the product of all complex quantities with the factor e-iωtapplies.The linearized form of the free-surface condition is

where K=ω2/g is deep water wave number,and g is the acceleration of gravity.The velocity potential of the incident wave is defined by

The linearization of the problem permits the decomposition of the velocity potential φ into the radiation （φR）and diffraction （φD）components;while diffraction potential （φD）includes incident potential （φ0）and scattering potential （φ7），the velocity potential φ can thus be expressed in following:

The constant ξjdenotes the complex amplitudes of the body oscillatory motion in its six rigid-body degrees of freedom,and φjdenotes the corresponding unit-amplitude radiation potentials.The velocity potential φ7represents the scattered disturbance of the incident wave by the body fixed at its undisturbed position.On the undisturbed position of the body boundary,the radiation and diffraction potentials are subject to the conditions:

3 Boundary integral equation

The boundary value problem(Eq.1 to Eq.7)of radiation and scattering potential above can be solved in terms of forming integral equation on body surface through Green second theorem.The radiation potential should satisfy following equation on body surface:

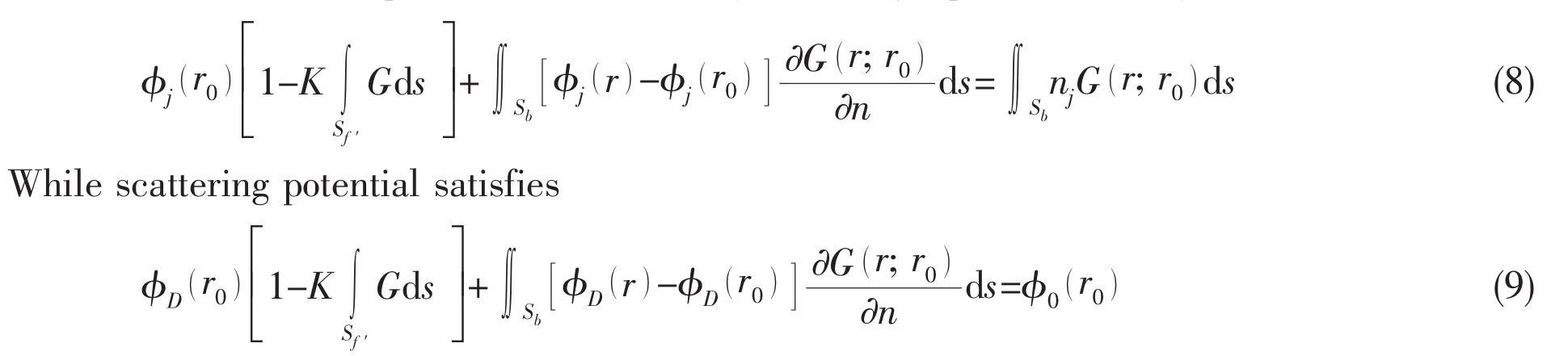
here r=（x,y,z ）denotes field point,r0= （ξ,η,ζ ）denotes source points,Sbdenotes body wetted surface in calm water.From the computational point of view,equation(9)has some advantages over equation(8)in terms of CPU time and the requirement of storage space,because of the relative simplicity of the right-hand side.The Green function G（ r; r0）is referred to as the wave source potential.It is the velocity potential at the point r due to a point source of strength-4π located at the point r0.It satisfies the free-surface and radiation conditions,and in finite water depth is defined by

here J0（）is the Bessel function of zero order.In equation(10)the Fourier k-integration is indented above the pole on the real axis in order to enforce the radiation condition.The calculation of Green function and wave body radiation and diffraction are referred to Newman(1985,1986,1988).

4 Formulation discretization

The integral equations are approximated by discretizing the surfaces of integration by boundary elements.The surfaces cover the body and interior water plane area.The values inside an element are represented in terms of nodal values and shape functions.On the discretized body surface and on the inner water plane area,both triangular and quadrilateral elements are used.By introducing shape function hi（ξ, ）η in local intrinsic coordinates in an element，a variable and its derivatives can be represented by the values at the nodes as follows:

where s is the number of nodes in the element.Using the shape functions above and the transformation relationship between local intrinsic coordinates and the global coordinates,we can discretise the integral equation for the first order problem as：

here J（ ξ,η ）is the Jacobian for the coordinate transformation.NBand NF′are the numbers of elements on the body surface and on the interior water plane area respectively.

5 Formulations of mean wave drift force

The mean wave drift force is crucial to mooring system of FPSO.Normally there are two methods to calculate mean wave drift force:far field method and near field method(Kim,Yue,1990;Kashiwagi,Endob,Yamaguchi,2005).Far field method can obtain three components in horizontal plane:surge,sway and yaw;while near field method can obtain the whole six components:surge,sway,heave,roll,pitch,yaw.Far field method can get surge and sway mean wave drift forces with very high precision but yaw moment converges slowly.Yaw mean drift force can be approximated by two dimensional slip-method with fairy good result for slender body,but to FPSO and TLP type platform with complicated body geometry,yaw moment is not easily converged in the range of high wave frequency.The other disadvantage of far field method is that it can only obtain a final total force whether the single or multiple bodies are considered.Near field method calculates wave force through pressure integration upon the whole body surface,it can get all six components of wave force with converged results with enough element number and higher-order method.The drawback of near field method is that it needs very complicated mathematical manipulation.Here we use near field method and the formu-

lations to calculate the mean wave drift forcesand momentsare listed as follows:

6 Analysis of mean wave drift force of FPSO

From viewpoint of engineering application,the horizontal plane mean wave drift force surge，sway and yaw are thought to be the crucial criterion for designing of mooring systems of FPSO.This section discusses mean wave drift force of one kind of Schiehallion type FPSO currently working in NorthSea of England.Considering regular incident wave with unit amplitude,the wave direction is listed in Fig.1.The longitude of FPSO is 238m,width is 45m,draft is 11.5m,water depth is 240m,the gravity center of vehicle is 5.96 under water line.Fig.2 is the mesh of FPSO,since symmetry method is utilized only one plane mesh plot is given.In each symmetry plane the total element number is 420 and the number of control node is 915.

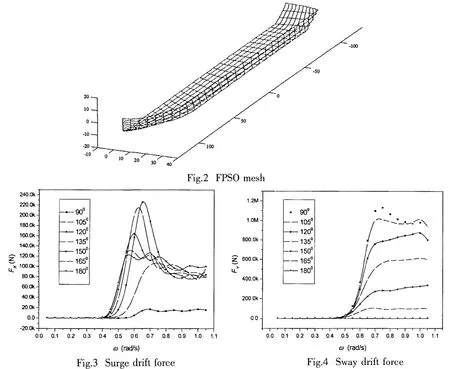
Fig.3 Surge drift force Fig.4 Sway drift force

Figs.3-5 show mean wave drift forces and moments surge,sway and yaw of FPSO under different incident waves.Wave drift force means continuous average wave resistance acting on body.In these figures,x axis means shallow water wave frequency,y axis means wave force or moment,they are both expressed with dimensional form.The surge and sway drift forces are both minus under current wave direction,but in order to make the description easily we discuss drift force based on formulation FX=-X,FY=-Y.In each wave direction,the frequency interval is 0.05 and totally 21 frequencies in the range between 0 to 1.05 are calculated.

From Figs.3-5,it can find that when ω＜0.4,mean wave drift forces are very small and FPSO is always in steady motion under any wave direction;generally for ω＞0.4,surge,sway and yaw drift force or moment will increase with frequency but converge to different values for ω＞1.0.Around frequency ω＞1.0,the sway drift force will decreasingly converge to different constants with increasing of wave directions.Under this situation for ω＞0.4,if FPSO is not efficiently constrained,it will move slowly from its initial position.While in the range 0.4＜ω＜0.8,drift forces and moment vary rapidly and 0.05 frequency interval is still large for the calculation of second order wave loads.Although the wave directions are different,the maximum values of surge,sway and yaw drift forces or moment are occurring in frequency ranges 0.55＜ω＜0.7 which corresponding to wave period 8.97s＜T＜11.4s.

From Fig.3,in the frequency range 0.4＜ω＜0.8,the wave directions causing larger surge force are around 120°≤β≤150°,even though the maximum value of surge does not exist in this field but the whole surge force within this range varies slightly and from the viewpoint of ship manipulation,it is easy to control its motions;for ω＞0.8,the surge force will decreasingly converge to constant values under wave directions 105°≤β≤180°,the force value is between 8.0×104N and 1.0×105N.To beam wave direction β=90°,the surge force is very small but not equal to zero,this is mainly because the geometry of FPSO is symmetric to x axis not y axis.This finding reveals the precision of model meshing and application of higher order boundary element method guarantees the drift forces converge efficiently at high frequency when ω＞0.8.

To sway drift force,the varying tendency is similar to surge drift force,the difference is that when ω＞0.8 for different wave directions,the sway drift force will increase with frequency and converge to different values around frequency ω＞1.0.The final steady values of sway drift force increase from head wave to beam wave and the beam wave β=90°will produce maximal force.Comparing with Fig.3 and Fig.4,the maximal surge drift force in beam wave is around 1.0×104N while maximal sway drift force is around 1.0×106N.The latter is nearly 100 times of the former.In head wave direction β=180°,the maximal surge drift force is around 2.2×105N while sway drift force is zero because of x axis symmetry of FPSO;at other wave directions,the relations of maximal sway drift force and surge drift force are:10 times(β=105°);4 times(β=120°);3 times(β=135°);2 times(β=150°);0.77 times(β=165°).From the respect of real working conditions of FPSO,the maximal surge drift force is around 2.2×105N(β=180°）and maximal sway drift force is around 1.0×106N （β=90°）,the sway drift force is 5 times of surge drift force.

Comparing to Fig.3 and Fig.4,Fig.5 is the result of yaw drift moment and has complicated varying curves.Generally it can find that at frequency ω＜0.4,MZ=0 exists under any wave directions which means FPSO at this time is in absolutely safe motion condition.But it should be pointed out that at frequency ω=0.3,an irregular frequency occurs which will cause resonance of body motion at low wave frequency.At frequency ω＞0.8,only head wave can be thought to be in steady condition since at this case the yaw drift moment is zero because of symmetry of FPSO.At beam wave the yaw drift moment is small but can not be ignored,the yaw drift moment at other wave directions are large.It also can be found that in high wave frequency,the surge and sway drift will converge to constant values,but yaw drift moment still varies with the changing of wave direction from head wave to beam wave,its tendency is following the changing of formulation ksin β×kcos β [Newman,1974],where k is wave number.

6 Conclusions

The precision of mean wave drift force of FPSO can be improved by higher-order boundary element method and considering geometrical symmetry.The surge,sway and yaw drift force are three important factors in design of mooring systems of FPSO.The most dangerous mean wave drift force occurs when wave incident direction is in the range 90°≤β≤135°,while wave frequency is in the range 0.4<ω<0.8.In order to control FPSO safely under severe sea condition,the FPSO systems should change its weathervaning angle to head sea all the time,since sway and yaw drift force are both zero under that time.

[1]Liu Yingzhong,Miao Guoping.Ship motion in waves[M].Shanghai:University of Shanghai Jiaotong Press,1986.

[2]Faltinsen O M.Sea loads on ships and offshore structures[M].Cambridge University Press,Cambridge,UK,1990.

[3]Ogilvie T F.Second order hydrodynamic effects on ocean platforms[C]//Inernational Workshop on Ship and Platform Motion.Berkeley,USA,1983:205-265.

[4]Maruo H.The drift of a body floating on waves[J].Journal of Ship Research,1960,4:1-10.

[5]Newman J N.The drift force and moment on ships in waves[J].Journal of Ship Research,1967,11(1):51-60.

[6]Newman J N.Second-order slowly varying forces on vessels in irregular waves[C]//Proc Int Symp Dynm Marine Vehicles Struct Waves.IMechE,London,1974.

[7]Newman J N,Sclavounos P D.The computation of wave loads on large offshore structures[C]//BOSS’88 Conference.Trondheim,Norway,1988.

[8]Newman J N.Algorithms for the free-surface green function[J].Journal of Engineering Mathematics,1985,19:57-67.

[9]Newman J N.Distribution of sources and dipoles over a quadrilateral[J].Journal of Engineering Mathematics,1986,20:113-126.

[10]Kim M H,Yue D K P.The complete second-order diffraction solution for an axis-symmetric body.Part 2:Bi-chromatic incident waves and body motions[J].Journal of Fluid Mechanics,1990,211:557-593.

[11]Kashiwagi M,Endob K,Yamaguchi H.Wave drift forces and moments on two ships arranged side by side in waves[J].Ocean Engineering,2005,32:529-555.

应用高阶边界元法求解FPSO型采油平台波浪漂移力的研究

王 科，张志强，许 旺

（大连理工大学工业装备结构分析国家重点实验室，工程力学系，辽宁 大连116024）

波浪平均漂移力是影响FPSO系统系泊、立管安装和卸载的重要外在荷载。文中针对英国北海正投入使用的萨哈林型式FPSO，应用高阶边界单元方法对其二阶水动力特性进行了计算分析，计算中考虑了物体的几何对称性，FPSO系统所受到的纵荡，横荡以及首摇方向的波浪平均漂移力采用近场解法在湿表面上直接进行压力积分获得。与常数单元方法相比，该方法具有很高的精度，特别是对于高频波浪能得到可靠的收敛解。研究表明为了使得FPSO系统在恶劣海况下安全使用，FPSO系统必须始终保持迎浪状态工作。

FPSO；波浪平均漂移力；高阶边界元方法；近场解法

U661.1 U674.38+1

A

王 科（1970-），男，大连理工大学工程力学系讲师；

许 旺（1983-），男，大连理工大学硕士生。

U661.1 U674.38+1

A

1007-7294（2010）06-0587-09

date：2009-08-21

Supported by the Scientific Research Foundation for the Returned Overseas Chinese Scholars,State Education Ministry,2007[24]

Biography：WANG Ke(1970-),male,lecturer of Dalian University of Technology,E-mail:kwang@dlut.edu.cn,Tel:0411-84707330.

张志强（1984-），男，大连理工大学博士生；