基于复杂网络理论的装备保障网络实证研究

张 勇, 杨宏伟, 白 勇, 王焕坤

(装甲兵工程学院技术保障工程系,北京100072)

基于复杂网络理论的装备保障网络实证研究

张 勇, 杨宏伟, 白 勇, 王焕坤

(装甲兵工程学院技术保障工程系,北京100072)

为更好地理解装备保障网络的拓扑结构及其特点规律,基于复杂网络理论构建了装备保障网络模型,并从无标度、小世界和层次性等方面具体分析了装备保障网络的统计特征。实证结果表明：装备保障网络具有一般复杂网络相似的拓扑特性,即无尺度特征、小世界效应、较为清晰的层次结构及负相关匹配特性。

复杂网络;装备保障网络;小世界效应;无尺度;拓扑结构

精确、持续、高效成为现代战争装备保障的最本质需求,与此同时,装备保障行动不再基于集合,保障方式开始从“线性计划”向“网络随机”转变,信息技术成为各种保障力量的“黏合剂”。将特定区域内的所有保障单元以某种方式耦合成一个庞大的动态网络,保障单元之间相互协调配合,最终实现“1+1＞2”的保障效果是未来装备保障建设的基本规律和发展趋势。根据研究对象和范围的不同,本文中“装备保障网络”特指由一定区域内(战区或全军)各保障实体(单位)以及其相互关系形成的一个网络。从某种意义上,装备保障网络是装备保障系统运行的基础,其结构对装备保障系统健康稳定运行、增加保障的时效性、提高装备保障整体效益都具有重要的作用。

获取装备保障网络各种性质是了解装备保障网络本质的基本起点,本文基于复杂网络理论,通过构建战区范围内装备保障网络模型,实证装备保障网络是否拥有复杂网络的统计特征,以便更好地认识装备保障网络的行为、改善其性能,为进行理论探索打下基础。

1 复杂网络理论及其典型统计参数

1.1 复杂网络概述

自然界中存在的大量复杂系统都可以用网络的形式加以描述。从网络科学的观点出发,系统中的每个个体均可以看作1个节点,个体之间的联系可抽象为1条边,从而系统中的具有关系的所有个体就构成了1个网络。特别是文献[1-2],发现了复杂网络中的无标度特征和小世界现象,使得现实生活中的很多复杂现象有了较为准确与合理的解释。目前,复杂网络理论在自然科学和社会科学等多个领域都得到了广泛的应用和研究[3-5]。

复杂网络理论在军事领域中的应用也得到了发展,文献[6]从学科交叉的角度分析了网络化战争与复杂网络研究的相似性与应用可行性。国防科技大学、国防大学等军内院校也纷纷加入到应用复杂网络理论研究军事领域相关问题的行列中[7-9]。仅就应用复杂网络实证军事领域相关网络而言,已取得了一些成绩,典型的有对网络化战争模型、军队指控系统模型、海战网络、防空网络等网络进行的实证分析。但是,单纯从复杂网络角度研究装备保障网络的文献还不多。文献[10]从级联失效的角度分析了保障网络(属后勤、装备综合保障网络)的抗毁性,并且认定保障网络既不是小世界网络也不是无标度网络,笔者认为单纯将保障网络映射到地理空间层面进行研究,不足以反映军事组织网络自身的社会属性和基本规律。例如,现实中2个相邻保障节点分别隶属于不同的上级保障单位,从而二者发生联系的可能性也不是很大。因此,军事领域中的各保障节点(文中特指装备保障节点)在具备一定空间属性的同时,还具备非常重要的业务属性,即保障节点上下级之间的支援、协同关系,这才是保障网络形成的基础和关键。正是基于上述考虑,本文尝试从业务属性层面构建装备保障网络,并通过典型的统计参数对装备保障网络的无标度、小世界等特性进行分析。

1.2 典型统计参数[11]

1)度和度分布。度：网络中节点vi的度ki定义为与该节点连接的其他节点的数目,所有节点的度的平均值称为网络的平均度,记为〈k〉。节点度衡量节点的重要程度,表征节点在网络中与其他节点交互程度,是节点最基本的特征,一般来说,网络中1个节点的度越大意味着这个节点在网络中越“重要”。度分布：网络中节点的度分布情况可用分布函数P(k)来描述,其含义为一个任意选择的节点恰好有k条边的概率,也等于网络中度为k的节点的个数占网络节点总数的比例。如果网络中节点度成幂律形式分布,则称该网络具有无标度特征。

2)聚集系数,也称簇系数,是衡量网络节点集聚程度的重要参数。节点vi的聚集系数Ci定义为节点vi的邻接点之间实际存在的边数与所有可能的边数的比值。假设网络中节点vi有ki条边将它与其他节点连接,而这ki个节点之间最多可能有ki(ki-1)/2条边数,那么这ki个节点之间实际存在的边数Ei和总的可能边数ki(ki-1)/2之比就定义为节点的聚类系数Ci,即

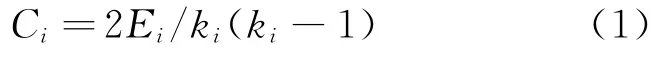
网络的聚集系数C为整个网络中所有节点的聚集系数的平均值,显然,只有在全联通网络(每个节点都与其余所有的节点连接)中,聚集系数才能等于1。

3)平均路径长度,也称平均距离。一般定义节点vi和vj之间的距离dij为连接二者所要经历的边的最小数目,其中用任意2点间的最大距离定义网络的直径(diameter),记为D。

网络的平均路径长度L定义为任意2个节点之间的距离的平均值,即式中N为网络节点总数。

上述3种统计参数是复杂网络研究的基础,事实上,复杂网络还存在着大量其他的统计指标,限于篇幅,本文不再赘述。

2 构建装备保障网络

2.1 概念建模

1)节点,按职能划分,装备保障网络中节点可代表管理机构、修理分队、器材保障分队和培训机构等保障实体;按专业兵种划分,可代表军械、装甲、车辆、船艇、工程、防化等专业保障实体。为了研究对象的普适性和统一性,文中设定装备保障节点为在一定的时间、空间范围内,具备接收和发出各种装备保障资源功能的实体单位。

2)边,代表节点(对象)之间的相互作用、相互关联。文中主要从业务层面构建装备保障网络模型。图1所示为业务结构层面与地理空间层面之间的对应关系,与现实空间拓扑网络不同的是,业务网络拓扑高于地理空间拓扑网络同时也源于地理空间拓扑网络。这主要是因为业务关系网络往往是抽象的、看不见的,它的功能的实现必须通过地理空间层的各种实体进行实现,如公路、铁路、水路、航线、管道甚至网线等。另外,本文设定所研究的装备保障业务网络为连通网络,即其对应的空间地理网络是连通的。如,图1中节点5和节点4间虽然没有直接的实体连接路径,但是由于二者存在业务关系,那么对应的业务负载可从节点5通过节点3或者节点6到达节点4。

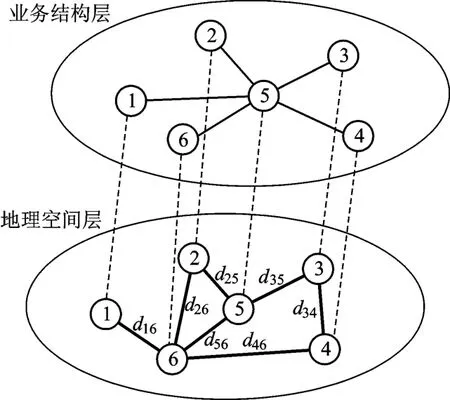
图1 装备保障网络结构示意图

3)网络拓扑,为了研究网络拓扑模型的性质,将该网络用一个矩阵来表示,也称网络结构邻接矩阵,以表征网络中各节点之间有无连接关系。如果用wi,j表示节点vi、vj连接情况,则

2.2 数据来源及处理

通过调研、部队实践等方式,笔者收集了大量关于部队装备保障实力的数据并进行了脱密和简化处理。本文主要做了2方面的设定：一是上下级之间为3∶3编制,即设定1个战区辖3个集团军,1个集团军辖3个师,以此类推;二是忽略各专业兵种的区别,仅从职能层面进行划分,即各级装备保障实体仅划分为管理、修理、供应、训练等4种保障实体。

为了对比分析,文中给出了严格树状拓扑结构条件下的装备保障网络(如图2(a)所示,160个节点、528条边)。对信息进行整理分析后,本文得到了一个包括160个节点、638条边的装备保障网络(如图2(b)所示)。

3 实证分析

3.1 无标度特征

由上述分析可知,节点的度分布反映了网络的整体性质,为证明其无标度特性,经计算得到装备保障网络双对数坐标下的度分布如图3所示。

图3 装备保障网络的度分布Log-Log图

使用非线性最小二乘法拟合其度分布曲线,装备保障网络的度分布基本服从P(k)～ak-γ,其中,具有严格树状拓扑结构的装备保障网络(以下简称网络模型a)γ≈1.758,实际调研装备保障网络(以下简称网络模型b)γ≈1.448,证明从业务层面构建的装备保障网络具有较明显的无标度特性。这是因为,从业务关系出发,装备保障网络中存在“度值较大的节点相对比较少,而度值较小的节点数目非常多”,如在一个局域装备保障网络中,通常有几个核心节点,如保障基地、装备保障指控中心等,大多数保障实体立足于保障本单位所属武器装备,度值较小。

值得说明的是,战时条件下,具备无尺度特征的装备保障网络面对随机攻击时具有很高的承受能力,而对关键节点进行攻击则具有极大的脆弱性。

3.2 小世界特征

复杂网络研究中另一个重要的发现是,绝大多数大规模真实网络的平均路径长度要比想象的小得多,这一说法来源于著名的Milgram“小世界试验”,即经典的“六度分隔”理论的起源。按照文献[1]的观点,所谓小世界特征就是具有较大的聚类系数和较小的平均路径长度。这里较大的聚类系数指真实网络的聚类系数远大于相同规模的随机网络的聚类系数;较小的平均路径长度指平均路径长度随网络规模的增加呈对数(L～ln N)或者更小增长,见表1。

表1 装备保障网络小世界统计特性

通过上述结果可知,装备保障网络的聚集系数远大于同等规模的随机网络,并且相对于节点总数为160的网络规模,具有较小的平均路径长度,从而装备保障网络具有明显的小世界特征。这一特征使得装备保障网络中各种保障资源的流动、共享与同步变得相对简单,有利于对各种突发事件做出快速响应,实现装备保障网络效益的最大化。

3.3 层次结构特性

为更加清晰地了解装备保障网络结构,本文借鉴文献[12]的观点来考证其层次结构特性,具体来说,可通过计算度数为k的各节点的平均聚类系数

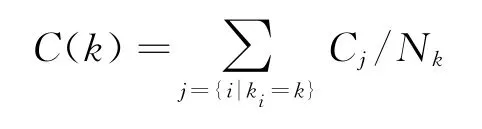
式中Nk是度数为k的节点个数,它量化网络的层次结构。

图4给出了C(k)随k的分布图。不难发现, C(k)是k的递减函数,且在k比较大时具有非常明显的层次结构。值得注意的是在k比较大时, C(k)随k的分布斜率近似为0,说明度数大的节点能够很好地聚类,而在k比较小时,C(k)随k的分布斜率约为0.062 5,表明度数小的节点此时属于不同的群体(community),群体之间的连接较为稀疏。因此,装备保障网络的层次结构明显区别于随机无标度网络(节点度具有无标度分布但不具有层次结构的网络)。

图4 装备保障网络的层次结构特征

3.4 度相关性

网络中节点的度相关性表征节点之间相互选择的偏好程度,这种度相关性描述了网络中不同节点之间的连接关系,如果度数大的节点倾向于连接度数大的节点,则称网络是正相关的;反之,如果度数大的节点倾向于和度数小的节点连接,则称网络是负相关的。其中,1个节点所有邻近节点的平均度记为

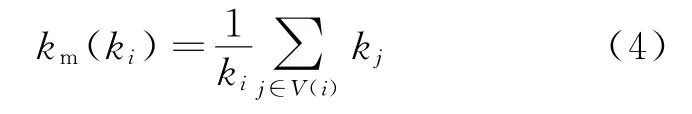
式中V(i)表示节点vi所有邻近节点组成的集合。则度数为k的所有节点(Nk)的邻近平均度为

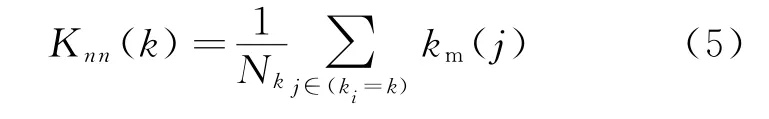
如果Knn(k)随着k递增,即度数大的节点优先连接度数大的节点,则网络是正相关的;反之,如果Knn(k)随k递减,度数大的节点优先连接度数小的节点,则意味着网络是负相关的(如图5所示)。

通过图5可以发现,装备保障网络中Knn(k)整体随着k递减,呈负相关连接趋势,表现为节点度数较大的节点倾向于连接度数小的节点。但同时发现耦合效果并不是特别理想,一方面可能与实验数据量的规模有关,另一方面也可能与装备保障网络度相关性程度不高有关。

图5 节点度度相关性

4 结 论

本文基于复杂网络的视角对装备保障系统进行建模,用节点和边将装备保障系统抽象成一个复杂网络,并对该网络结构的基本统计特征进行分析,得出如下结论：

1)装备保障网络具有无标度特征,网络中存在一些度值很大的保障节点,从而使整个网络在面对不同攻击模式时表现出既鲁棒又脆弱的特性。

2)装备保障网络具有小世界特性,不同节点之间连接紧密,平均路径较小,有利于装备保障网络的协同和支援效能的发挥。

3)装备保障网络具有层次结构并且具有负相关匹配特性,其中层次结构表明装备保障网络中各保障实体相互关联形成一个个小的群体,然后逐步连接成一个大群体;负相关匹配特性表明度大的节点更容易连接度小的节点,也就是中心保障节点能够对其他保障节点施加足够的影响。

References)

[1]WATTS D J,STROGATZ S H.Collective dynamics of“small-world”networks[J].Nature,1998(393)：440-442.

[2]BARABÁSI A L,ALBERT R.Emergence of scaling in random networks[J].Science,1999,286：509-512.

[3]STROGATZ S H.Exploring complex networks[J].Nature, 2001(410)：268-276.

[4]ALBERT R,BARABÁSI A L.Statistical mechanics of complex networks[J].Review of Modern Physics,2002,74(1)：47-97.

[5]NEWMAN M J.The structure and function of complex networks[J].SIAM Review,2003,45(1)：167-256.

[6]李德毅,王新政,胡钢锋.网络化战争与复杂网络[J].中国军事科学,2006,19(3)：111-119.

[7]吴俊,谭跃进.复杂网络抗毁性测度研究[J].系统工程学报, 2005,20(2)：128-131.

[8]胡晓峰,李志强,贺莜媛,等.复杂网络：战争复杂系统建模仿真新途径[J].装备指挥技术学院学报,2009,20(2)：1-7.

[9]朱涛,常国岑,施笑安.基于复杂网络的指挥信息系统拓扑模型研究[J].系统仿真学报,2008,20(6)：1574-1581.

[10]李勇.物流保障网络级联失效抗毁性研究[D].长沙：国防科技大学,2009：3.

[11]汪小帆,李翔,陈关荣.复杂网络理论及其应用[M].北京：清华大学出版社,2006：10-14.

[12]蔡世民,洪磊,傅忠谦,等.基于复杂网络的金融市场网络结构实证研究[J].复杂系统与复杂性科学,2011,8(3)：29-33.

(编辑：王高翔)

An Empirical Study on the Equipment Support Network Based on Complex Networks

ZHANG Yong, YANG Hongwei, BAI Yong, WANG Huankun

(Department of Technology Support Engineering,Academy of Armored Force Engineering,Beijing 100072,China)

The equipment support network is constructed based on the framework of complex network theory,and in order to well understand the topological structure and formation characteristics of the equipment support,the statistical properties of the equipment support network are analyzed from the scale-free,small world and hierarchy.The experiment results show that equipment support network has the similar topological attributes,such as scale-free behavior,small world effect,quite clear hierarchical structure and disassortativity.

complex networks;equipment support network;small world effect;scale-free;topology

E 9;N 94

2095-3828(2014)01-0083-05

ADOI10.3783/j.issn.2095-3828.2014.01.019

2013-03-06

张 勇(1984-),男,博士研究生.主要研究方向：装备保障系统运行与优化.zhywkh@163.com.杨宏伟,男,教授,博士生导师.