分离模块航天器自适应队形保持控制

李兆铭, 高永明, 牛亚峰, 廖育荣, 李 磊

(1.装备学院研究生管理大队,北京101416; 2.装备学院信息装备系,北京101416; 3.装备学院航天装备系,北京101416; 4.装备学院光电装备系,北京101416)

分离模块航天器自适应队形保持控制

李兆铭1, 高永明2, 牛亚峰3, 廖育荣4, 李 磊1

(1.装备学院研究生管理大队,北京101416; 2.装备学院信息装备系,北京101416; 3.装备学院航天装备系,北京101416; 4.装备学院光电装备系,北京101416)

针对分离模块航天器队形保持控制问题,采用模块航天器集群飞行动力学高精度模型,并考虑模块质量的不确定性和外部摄动干扰,设计了一种自适应队形保持控制器,实现了模块轨迹对标称轨道的跟踪,数值仿真验证了该控制器的有效性。

分离模块航天器;精确模型;队形保持;自适应;标称轨道跟踪

分离模块航天器是指将传统单个航天器分解为物理分离、自由飞行的模块航天器,通过无线自组织网络形成集群空间系统[1-5]。由于空间摄动干扰的存在,分离模块航天器长期被动飞行会积累队形偏差,严重影响模块间协同工作,甚至会发生模块间的碰撞。因此,对分离模块航天器队形保持控制的研究是十分必要的。文献[6]针对小卫星队形保持控制,使用Lyapunov势函数法设计了连续和离散2种控制器,实现了在规定时间内将绕飞星控制到理想位置。文献[7]考虑了空间摄动和推力误差等因素,采用Lyapunov最小-最大方法设计了队形保持的鲁棒控制器,实现了存在干扰情况下的队形保持控制。文献[8]以Lawden方程作为动力学模型,利用线性二次型性能指标最优控制实现了对卫星编队队形的保持。上述研究存在一个共同问题,就是没有考虑由于燃料消耗导致的卫星质量的不确定性。本文针对分离模块航天器队形保持控制问题,采用集群动力学高精度模型描述模块间相对运动,同时考虑了模块质量的不确定性和空间摄动干扰的影响,设计了一种自适应队形保持控制器,可以实现模块在空间的运动轨迹对标称相对轨道的跟踪。

1 模块集群飞行动力学模型

分离模块航天器采用集群飞行方式,为了方便分析集群航天器中各个模块间的相对运动,通常假设一个模块为参考模块,并将Hill坐标系固定在参考模块上,其他模块为伴飞模块。Hill坐标系定义如下：坐标系原点O位于参考模块的质心,x轴由地心指向参考模块,y轴在轨道平面内垂直于x轴,指向参考模块运动方向为正,z轴和x轴、y轴构成右手坐标系,如图1所示。

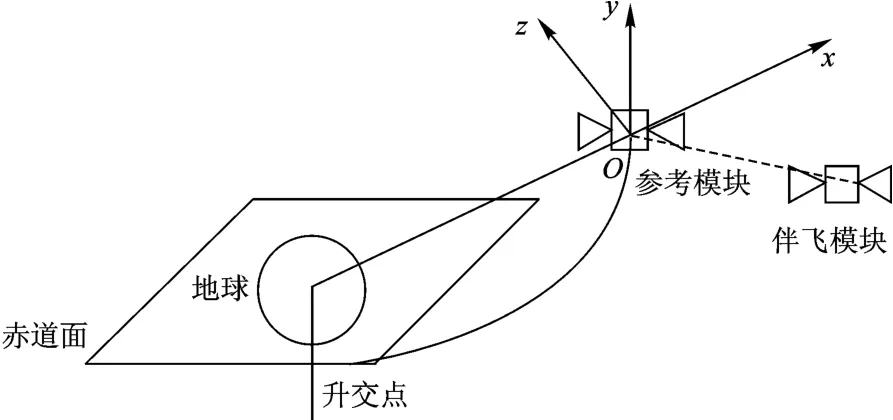
图1 Hill坐标系示意图

在Hill坐标系中分离模块航天器集群飞行轨道动力学模型[9]如式(1)所示。

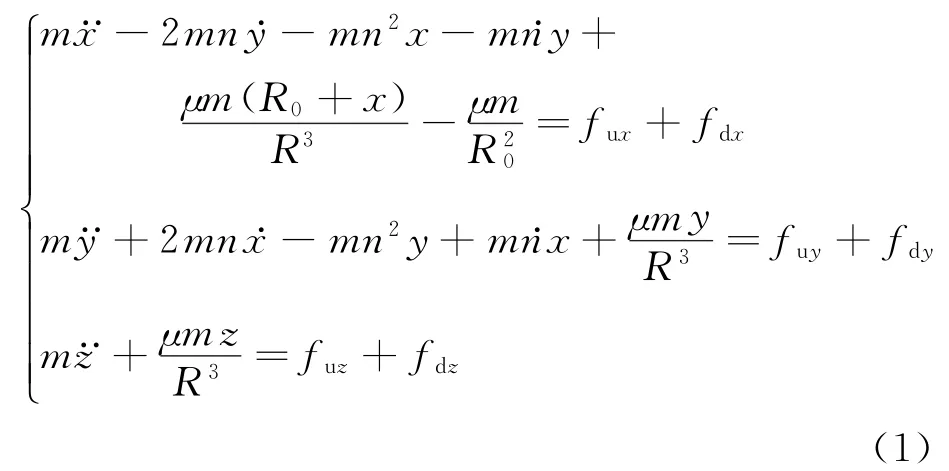
式中：R0为参考模块到地心的距离;R为绕飞模块到地心的距离;n为参考模块轨道角速度;m为模块质量;[fuxfuyfuz]T为模块控制输入; [fdxfdyfdz]T为模块所受空间摄动干扰; [x y z]T为绕飞模块在参考模块Hill坐标系中的位置。如果做如下定义：

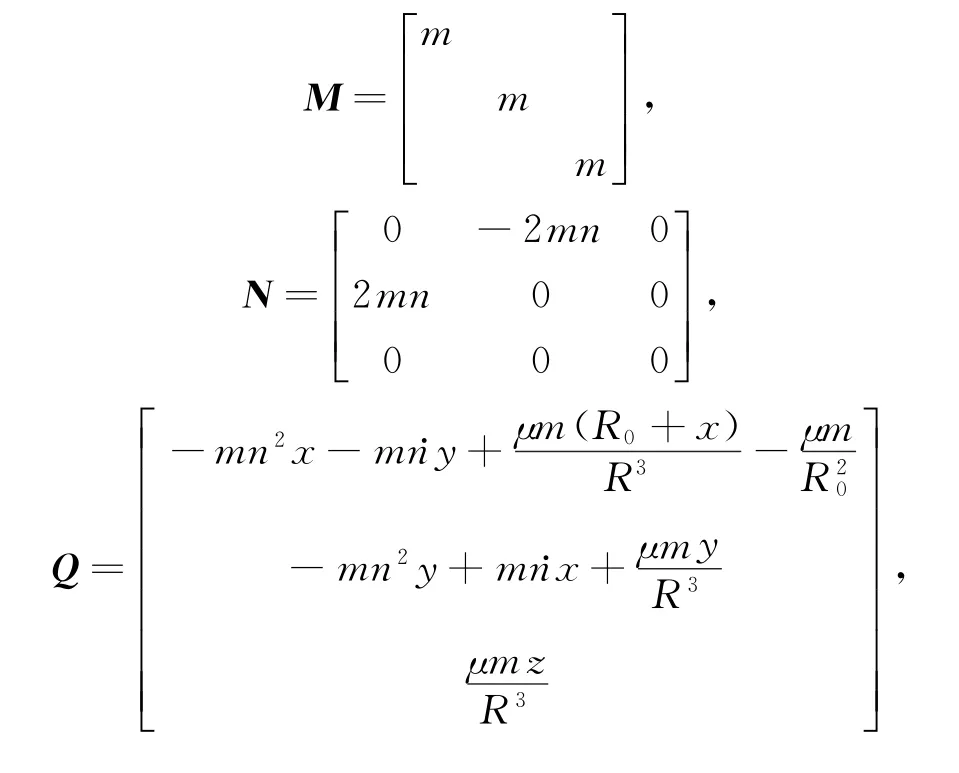
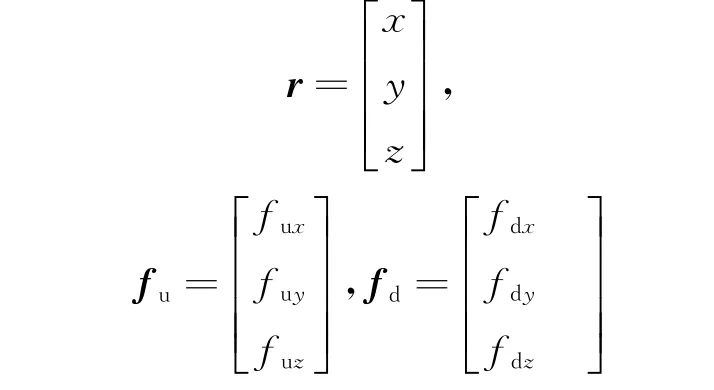
则式(1)可以写成如下的矩阵形式：

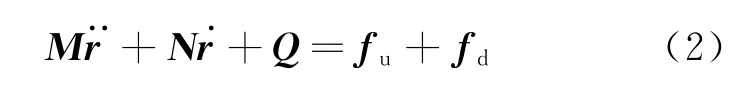
假设1 由于燃料消耗等导致无法得到模块质量的准确值。本文考虑模块质量是未知的有界常量,即R为模块初始质量。

2 自适应控制器设计及稳定性证明

2.1 控制器设计

定义标称队形为rd,则跟踪误差为re=rrd,控制器设计的目标是0。为了降低被控系统阶次,定义线性降阶滤波器,其中,λ＞0为设计参数,则,后式两侧同乘M并将式(2)代入得到如下等式：

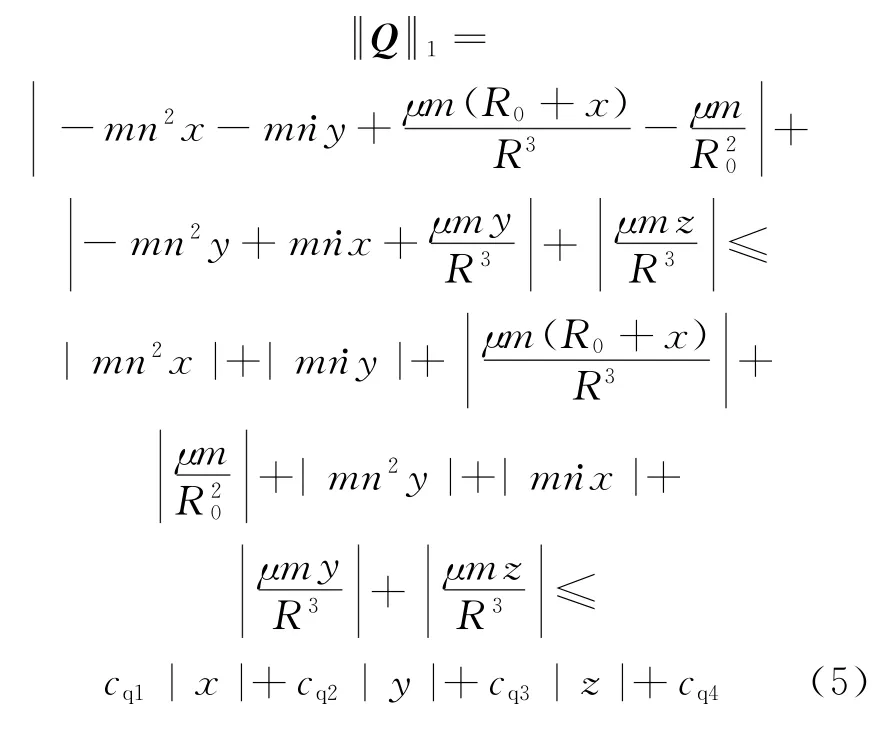
取Q的1范数为式中：cq1,cq2,cq3,cq4∈R为未知常量,取cq≥max(cq1,cq2,cq3)∈R,则式(5)可以化为

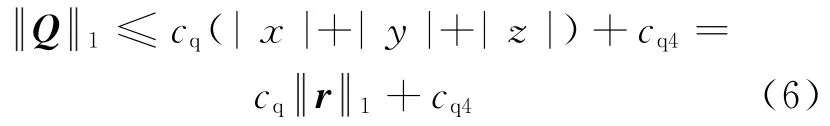
结合上述假设可以得到

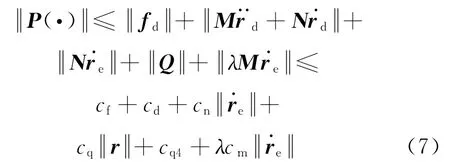
取ε≥max(cf+cd+cq4,cn+λcm,cq)∈R,则系统的不确定性集中体现在ε上,需要对ε进行自适应在线估计,同时这种设计可以大大减少在线计算量,减轻星载计算机的压力,定义σ=1+,则式(7)可以写成如下形式：

由此得到非线性项P(·)的上界,设计控制器如下：

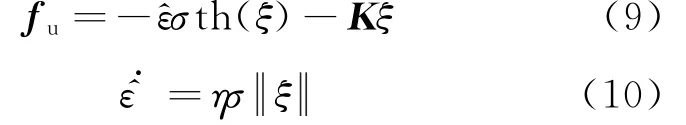
式中：ε^为ε的估计值;K∈R3×3为正定增益矩阵; η＞0为控制器设计参数;th()为双曲正切函数。则在控制器式(9)、式(10)的作用下,可以实现

2.2 稳定性证明

下面证明上述控制器是稳定的,定义Lyapunov函数如下：

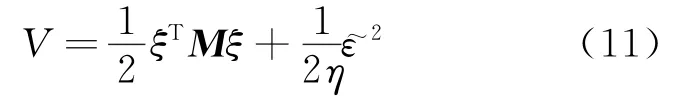
式中：ε～=ε-ε^为估计误差。由此可得ε

·～=-ε^·,对式(11)求导并将式(9)、式(10)代入得

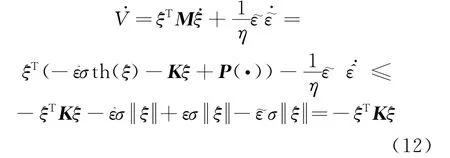
3 仿真算例

为了验证本文设计的控制器的有效性,基于Matlab/Simulink环境对模块编队飞行队形保持控制进行仿真。假设绕飞模块初始质量为50 kg,参考模块运行于轨道高度为1 200 km的圆轨道上,绕飞标称队形为rd=[200sin(0.001t) 400cos(0.001t) 60sin(0.001t)]T,绕飞模块初始位置为r0=(20 450 10)T,初始速度为v0= (0 0 0)T,控制器参数设计为λ=0.001,η= 10-7,K=diag[0.01 0.01 0.01],仿真时间为2个轨道周期,仿真结果见图2～图5。为了能够清晰地看到控制过程中相对位置等变化,图3～图5中只截取了前600 s的曲线。

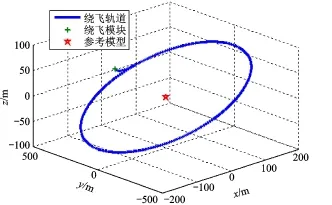
图2 模块跟踪轨迹

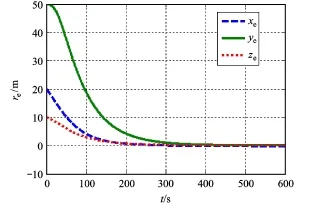
图3 相对位置误差

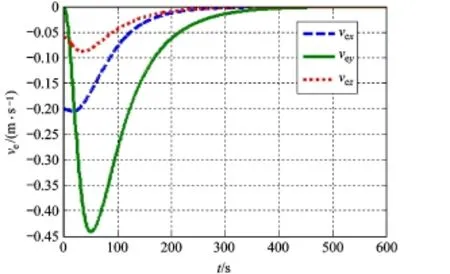
图4 跟踪速度误差

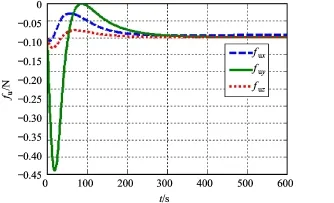
图5 输入的控制力

从图3～图5结果可以看出,模块从初始位置经过大概320 s跟踪标称轨道,机动路径曲线平滑,位置跟踪误差精度高,输入控制力幅值不超过1 N,可以满足小推力轨道控制要求。

4 结 论

本文针对分离模块航天器队形保持控制问题,采用集群飞行高精度动力学模型描述模块间相对运动,设计了一种自适应队形保持控制器并给出控制器稳定性证明,得到如下结论：

1)采用高精度模型描述模块间相对运动,避免了由于集群飞行模型不满足CW方程简化条件而带来的模型误差。

2)将模块质量不确定性和摄动干扰作为整体项进行自适应估计,设计了结构简单的自适应律,减轻了星载计算机的计算压力。

3)本文设计的控制器结构简单清晰,易于实现,仿真结果验证了该控制器的有效性,为航天器集群队形保持控制器设计提供了一定的参考。

下一步工作需要进一步研究多模块队形保持协同控制,以满足不同的任务需求。

References)

[1]YAO W,CHEN X,ZHAO Y.A fractionated spacecraft system assessment tool based on lifecycle simulation under uncertainty[J].Chinese Journal of Aeronautics,2012,25(1)：71-82.

[2]O’NEILL M G,WEIGEL A L.Assessing fractionated space

craft value propositions for earth imaging space missions[J]. Journal of Spacecraft and Rockets,2011,48(6)：975-985. [3]胡敏,曾国强.分离模块集群航天器发展概况[J].装备指挥技术学院学报,2011,22(4)：62-65.

[4]刘豪,梁巍.美国国防高级研究计划局F6项目发展研究[J].航天器工程,2010,19(2)：93-99.

[5]O’NEILL M G,YUE H,NAG S,et al.Comparing and optimizing the DARPA system F6 program value-centric design methodologies[R].Anaheim California：AIAA SPACE 2010 Conference&Exposition,2010：5-7.

[6]田继超,刘剑锋,崔乃刚.基于Lyapunov势函数的小卫星编队队形保持方法[J].上海航天,2006(2)：6-9.

[7]卢山,徐世杰.基于Lyapunov最小-最大方法的卫星编队飞行队形保持[J].航天控制,2009,27(2)：30-35.

[8]崔海英,李俊峰,高云峰.椭圆参考轨道的卫星编队队形保持控制设计[J].工程力学,2007,24(4)：147-151.

[9]马广富,梅杰.多星系统相对轨道的自适应协同控制[J].控制理论与应用,2011,28(6)：782-786.

[10]方勇纯,卢桂章.非线性系统理论[M].北京：清华大学出版

社,2009：41-42.

(编辑：李江涛)

Adaptive Control for Fractionated Spacecraft Formation Keeping

LI Zhaoming1, GAO Yongming2, NIU Yafeng3, LIAO Yurong4, LI Lei1

(1.Department of Graduate Management,Equipment Academy,Beijing 101416,China; 2.Department of Information Equipment,Equipment Academy,Beijing 101416,China; 3.Department of Space Equipment,Equipment Academy,Beijing 101416,China; 4.Department of Optical and Electronic Equipment,Equipment Academy,Beijing 101416,China)

For the problem of fractionated spacecraft formation keeping control,adopting precise model of fractionated spacecraft trunking flying kinetics,considering the module mass uncertainty and perturbation,an adaptive controller for module formation keeping is designed,the tracking of normal orbit is realized,and the effectiveness of the controller is shown by the simulation.

fractionated spacecraft;precise model;formation keeping;adaptive;tracking of normal orbit

V 412.4

2095-3828(2014)01-0065-04

ADOI10.3783/j.issn.2095-3828.2014.01.015

2013-06-07

部委级资助项目

李兆铭(1989-),男,硕士研究生.主要研究方向：分布式航天器协同控制.ilovemolly@163.com.高永明,男,副教授,硕士生导师.