双馈风电机组实测与标准功率曲线偏差影响因素分析*

文 | 宫玉鹏，苏丽营，赵海春，吴让慧，李磊，李超峰

双馈风电机组实测与标准功率曲线偏差影响因素分析*

文 | 宫玉鹏，苏丽营，赵海春，吴让慧，李磊，李超峰

风力发电因其具有系统安全性好、可靠性强、效率高及环保等独特优势，逐渐成为许多国家可持续发展战略的重要组成部分和研究焦点。2011年中国(除港、澳、台地区外)全年新增风电装机容量17.63GW，中国风电市场在历经多年的快速增长后正步入稳健发展期。全国累计装机容量62.36GW，继续保持全球风电装机容量第一的地位。随着风力发电在中国的快速发展，风电机组功率曲线测试的分析和研究工作也在逐步开展，相继修订了一些行业规范和国家测试标准。由于风电机组的设计研究工作处于起步阶段，而且设计研究和性能测试处于分离状态，所以导致行业内对减小标准和实测功率曲线误差的研究工作进展缓慢。影响风电机组的实测和标准功率曲线偏差的原因很多，通过对测试数据和仿真数据的分析与研究，发现风电机组环境和风电机组控制策略对功率曲线偏差有影响，以下将对这些影响因素进行深入地研究和分析。

标准功率曲线与实测功率曲线

标准功率曲线是在标准工况下，根据风电机组设计参数计算给出的风速与有功功率的关系曲线。标准功率曲线所对应的环境条件是：温度为15℃，1个标准大气压(1013.3hPa)，空气密度为1.225kg/m3。标准功率曲线只是通过静态的模拟计算获得，未考虑其他可能影响到风电机组功率曲线的因素。

实测功率曲线是按照IEC 61400－12标准要求，通过采集风电机组的电压、电流及测风塔的风速、气压、温度等信号，通过相应的计算方式，按照标准要求的空气密度1.225 kg/m3推算出的功率曲线。

环境对功率曲线偏差的影响

根据贝兹理论，风电机组从风能中吸收的功率p为∶

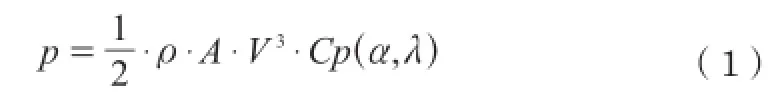
p －风电机组发电功率； ρ－空气密度；A－风电机组叶轮扫掠面积； V－风速； Cp－风电机组的功率系数； α－桨距角；λ－叶尖速比（ωmR/V , ωm为叶轮转速，R为叶轮转动半径）。

根据IEC 61400－12标准，空气密度的计算方式为：

B10min－大气压力10min平均值； R0－干燥的气体常数287.05J/(kg*k)； T－绝对温度10min平均值

针对有功功率控制的风电机组，风速的规格化使用如下公式进行：

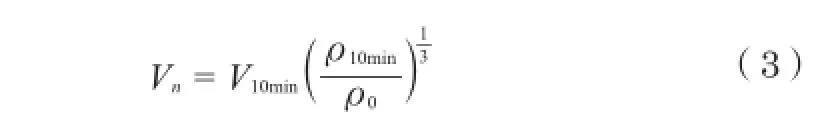
Vn－规格化的风速； V10min－测量风速10min平均值；ρ10min－测量空气密度10min平均值；ρ0－标准空气密度（1.225Kg/m3）

根据公式（1），（2），（3）可以得到如下功率计算公式：

根据公式(4)所示，随着海拔高度的增加，气压在逐渐降低，风电机组的额定发电功率逐渐下降；随着温度的下降，风电机组的额定发电功率逐渐上升。图1为相同型号的风电机组不同海拔高度的功率曲线，两条实测功率曲线要明显低于标准功率曲线，海拔越高实测功率曲线下降的越厉害；图2为东北地区同一台风电机组，由于冬季和夏季温度差异的原因，冬季的功率曲线要比夏季的功率曲线好很多，而且更容易接近标准功率曲线。

风电机组控制方式对功率曲线偏差的影响

风电机组的功率控制方式对风电机组的功率曲线有着至关重要的影响，不但可以减小对风电机组塔架的影响，而且可以适当减小其他部件的疲劳载荷，并且会大大提升风电机组的功率曲线和功率系数。

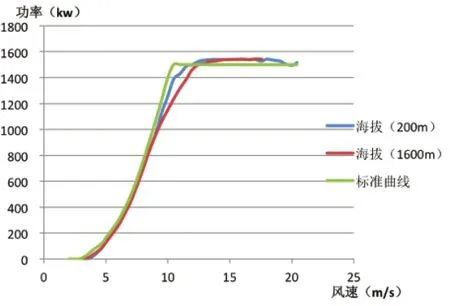
图1 海拔高度对功率曲线的影响

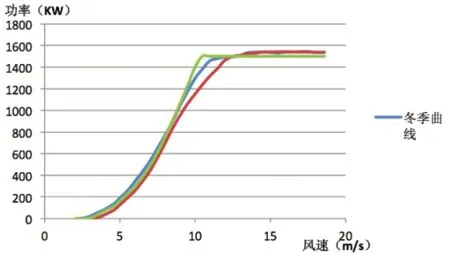
图2 温度对功率曲线的影响

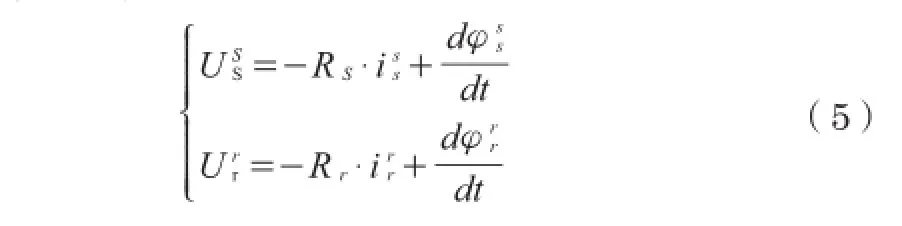
根据双馈电机模型，定子取发电机模式，转子取电动机模式，公式如下：－定子坐标系定子电压；Rs－定子坐标系定子电阻；－定子坐标系定子电流－定子坐标系定子磁通；－转子坐标系转子电压；Rr－转子坐标系转子电阻；－转子坐标系转子电流；－转子坐标系转子磁通。

由于定子与转子均在不同的坐标系下，所以要将公式（5）换算到同步旋转坐标系下：

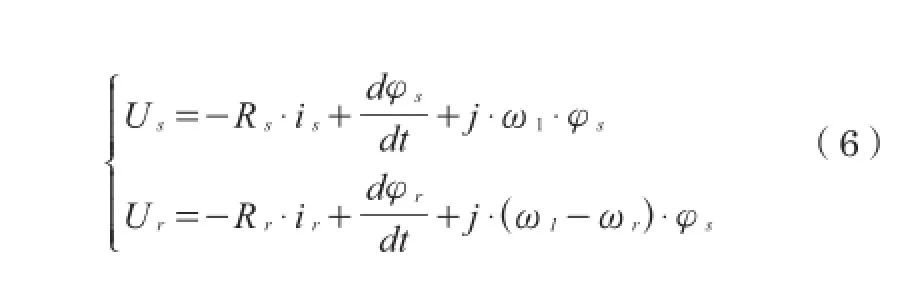
US－定子电压；RS－定子电阻；iS－定子电流；φS－定子磁通；ω1－定子旋转电角速度；Ur－定子电压；Rr－转子电阻；ir－转子电流；φr－转子磁通；ωr－转子旋转机械角速度。

根据d－p坐标变换，将定子电压定在d轴，当定子连接电网，发电机的电磁转矩为：

Te－发电机的电磁扭矩；np－发电机的极对数；Lm－发电机互感；Ls－发电机定子电感；im－发电机励磁电流；idr－发电机转子d轴电流。

根据风电机组转矩平衡公式：

J为风电机组传动链的转动惯量。

风电机组的电磁扭矩Te的大小是由发电机的转子d轴电流所决定的，而转子d轴电流是由发电机的转速差Δωr经过PID计算得到的。根据公式（9）可以看出，所有的项都是ωr的函数，说明ωr测量的准确性直接影响到风电机组的转矩控制。由于自然界的风速是不停变化的，所以导致风电机组的转速也随着不停变化，这就给ωr的准确测量带来很大的误差，也就会导致产生电磁扭矩的误差ΔTe。同时，由于风电机组是一个大惯性系统，转速变化速度无法跟随风速的变化速度，导致风电机组叶轮无法吸收到最大风能，势必会产生输入扭矩的误差ΔT。所以由公式（9）可得，

图3是一组在不同风速( v1 ＞ v2 ＞ v3 )下风电机组的输出功率特性，popt曲线是各风速下最大输出功率点的连线，即最佳功率曲线。

可以看出，由于机械转矩与电磁转矩的误差ΔT’的存在，追踪的“最优曲线”比理想的最佳曲线上下平移了ΔT’·ωr的偏差，如图4所示。ΔT’·ωr＞0，机组跟踪的是图中的popt1曲线；ΔT’·ωr＜0，跟踪的是popt2曲线。由于ΔT’·ωr存在，popt1或popt2都比较接近理想最佳曲线，但都不是最优功率曲线，获得的最大风能追踪控制效果与标准最佳功率曲线有一定偏差。

标准与实测的发电机电磁扭矩与转速的关系曲线如图5所示，可以看出标准数据和测试数据有较大偏差。由于控制器设计原因，无法保证风电机组在实际发电过程中严格按照设计最优值运行，必然将会导致标准功率曲线与实测功率曲线的偏差。

图3 风电机组的最佳功率特性

图4 最大风能追踪误差

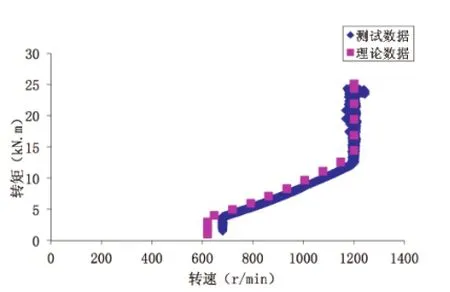
图5 发电机转矩与转速关系

通过对风电机组的测试数据进行分析，逐步降低ΔT’的绝对值，达到优化风电机组功率曲线的目的。如图5所示，东北某风电场对1.5MW风电机组进行优化后，可以看出风电机组在小功率运行时优化效果比较明显，基本接近标准功率曲线；当风电机组运行在额定功率时，优化测试曲线与标准功率曲线还是有较大偏差。转矩偏差对功率曲线的影响见图6。

结论

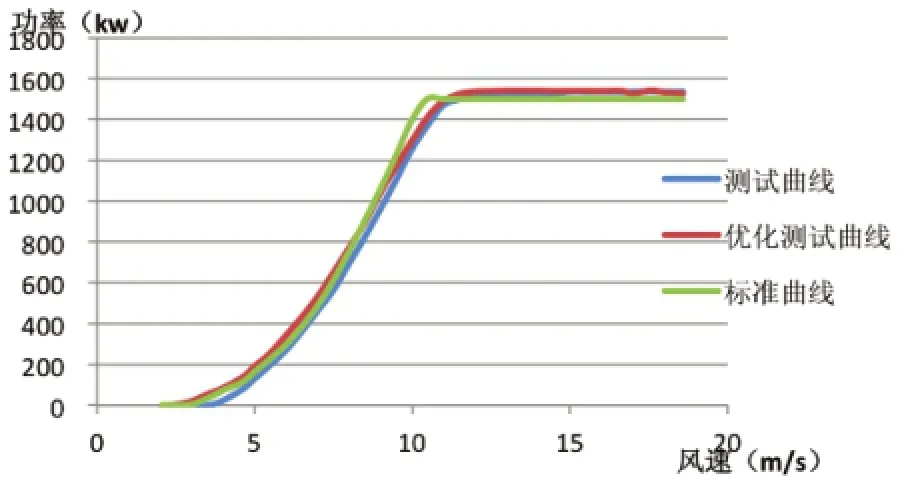
图6 转矩偏差对功率曲线的影响

由于风电机组的实际测试功率曲线受到风电机组环境和控制策略的影响，导致风电机组实际测试的功率曲线与标准功率曲线存在着很大的偏差。通过对两个主要影响偏差的因素进行分析后可知，在实际运行过程中可以采取相应的手段，来减小偏差的存在。希望可以提供一些理解风电机组功率曲线偏差的思路，为以后改善实测功率曲线起到应有的作用，并为完善相应的测试标准和检测评估体系提供一定指导。在后续研究工作中，在不断减小功率曲线偏差的情况下，应利用仿真或者测试来评估减小偏差是否会对风电机组其它部件造成很大的影响，并且针对功率曲线的偏差，应该更深入的从空气动力学、叶片翼型、变桨控制策略和功率控制策略等多个方面进行考虑。

(作者单位：华锐风电科技（集团）股份有限公司)

国家能源应用技术研究及工程示范项目（NY20110401-1）