1维非定常对流扩散方程的有理型高阶紧致差分格式

赵 飞，蔡志权，葛永斌

(宁夏大学数学计算机学院，宁夏银川750021)

0 引言

在处理流体流动和传热、温度扩散、海水盐度及地下水污染物质的扩散等实际问题中，很多都可归结为求解对流扩散方程.由于实际问题往往比较复杂，精确解很难求出，因此研究其精确、稳定和高效的数值方法具有十分重要的意义，有限差分方法是最常用的一种数值方法［1-13］.针对1维非定常对流扩散方程，文献［1］构造了1种对角元严格占优的Crank-Nicolson差分格式，文献［2］提出了 1种Crank-Nicolson特征差分格式，文献［3］提出了1种摄动有限差分方法，文献［4］建立了1类指数型交替显式方法.遗憾的是这些方法在空间上的整体精度均不超过2阶.近年来，已经发展了许多高阶紧致差分格式.比如，文献［5］通过引入1个综合变换，将对流扩散方程变为纯扩散方程，然后利用求解扩散方程已有的4阶格式，最终得到了1种求解对流扩散方程的2层高阶紧致隐格式，文献［6］利用4阶精度的3次样条公式，提出了1种求解非线性对流扩散方程的2层紧致隐格式，文献［7］由定常对流扩散方程的4阶紧致格式出发，将时间导数项作为非齐次项处理，建立了求解1维非定常对流扩散方程的1种2层高阶紧致隐式差分格式，文献［8］给出了求解1维含源项非定常对流扩散方程的1种3层全隐格式，即可适用于线性又可适用于非线性对流扩散问题的求解，文献［9］基于Hermite插值多项式的构造思路，推导出了1维非定常对流扩散方程无条件稳定的指数型高精度紧致差分格式.这些格式在空间上均具有4阶精度，时间上均具有2阶精度.

本文针对1维非定常对流扩散方程，结合已发展的求解非定常对流扩散方程的高阶紧致差分格式的基本思想，建立1种无条件稳定的有理型高阶紧致差分格式，给出格式的稳定性分析和证明，并通过数值算例验证本文方法的精确性和可靠性.

1 高阶紧致差分格式的建立

考虑如下1维非定常对流扩散方程:

初始条件为u(x，0)= φ(x);边界条件为u(b1，t)=g0(t)，u(b2，t)=g1(t).(1)式中，a为扩散项系数，p为对流项系数.假设函数u(x，t)在给定计算区域内足够光滑.

将空间求解区域［b1，b2］进行网格剖分为N个子区间:b1=x0＜x1＜x2＜…＜xN=b2，空间步长定义为h=(b2-b1)/N，用τ表示时间步长.

为了方便格式推导，首先考虑如下1维定常对流扩散方程:

a和p为常数，u，s均为x的函数，将点ui+1和ui-1在点xi处利用泰勒级数展开，可得

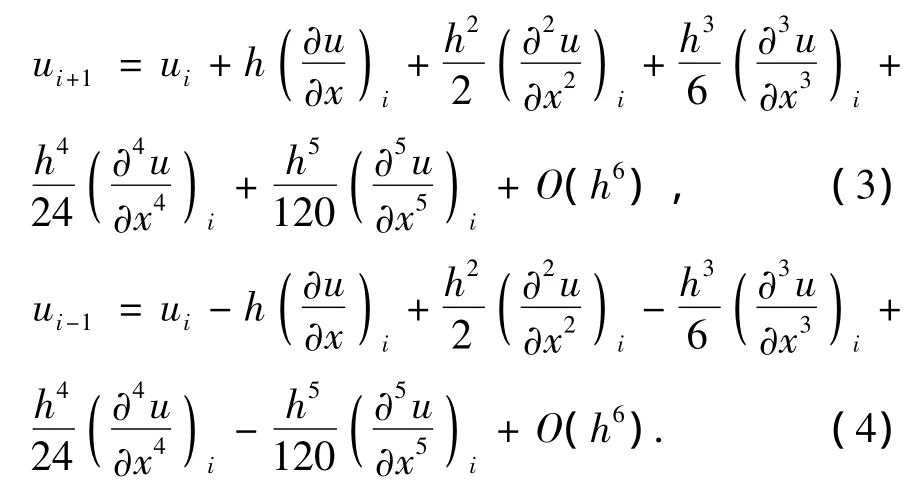
将(3)式和(4)式相减，整理后可得

将(3)式和(4)式相加，整理后可得

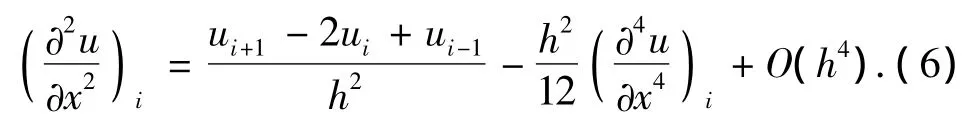
由此定义空间1阶导数和2阶导数的中心差分算子为

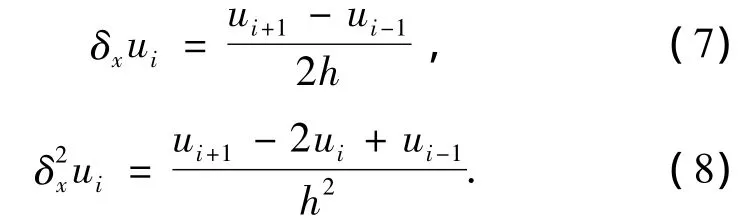
将(5)式与(6)式代入(2)式，并利用关于u的1阶导数和2阶导数的定义，可得

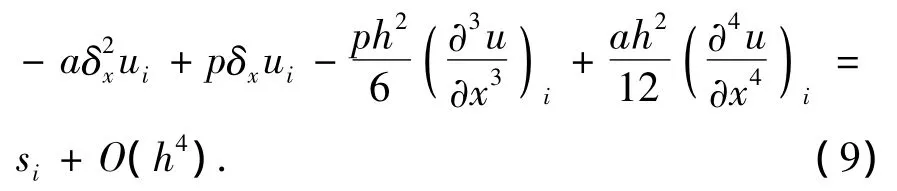
为了得到高精度的差分格式，将(9)式中的3阶导数项和4阶导数项进行处理，为此对原方程(2)关于x求导数，整理可得

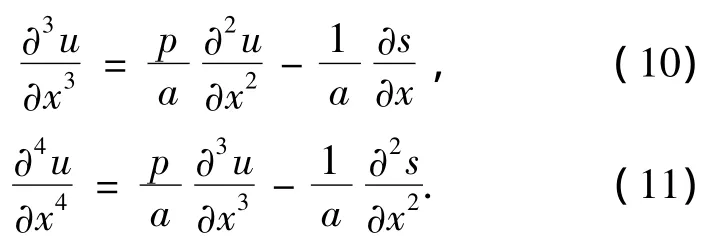
将(10)式代入(11)式，整理可得

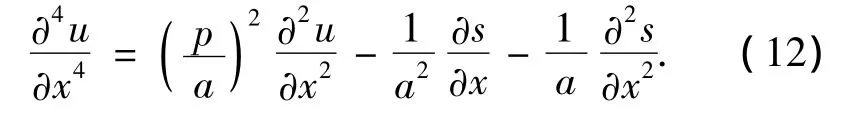
将(10)式和(12)式代入(9)式，并利用(7)式和(8)式对u的1阶导数和2阶导数进行离散，整理可得

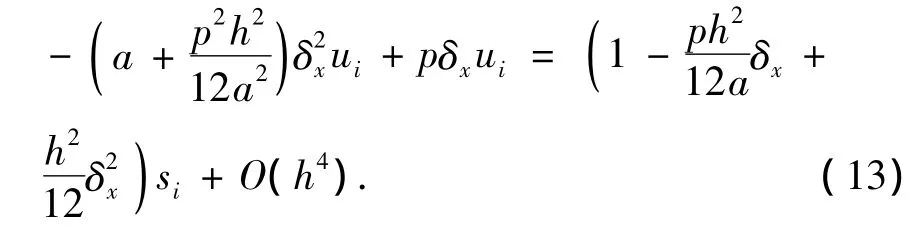
事实上，(13)式即是求解1维定常对流扩散方程的多项式型高阶紧致差分格式［10-12］.然而，文献［13］指出了此格式不能用于求解高雷诺数问题和纯对流问题.为此，把(2)式代入(12)式，整理可得

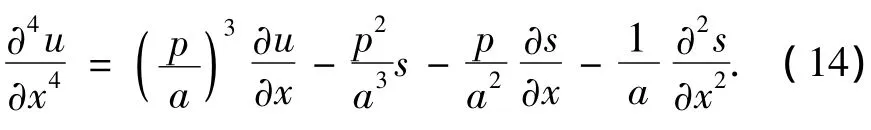
为了得到求解1维定常对流扩散方程的有理型高阶紧致差分格式，对(9)式做如下处理.首先，将(10)式和(14)式代入(9)式，整理可得

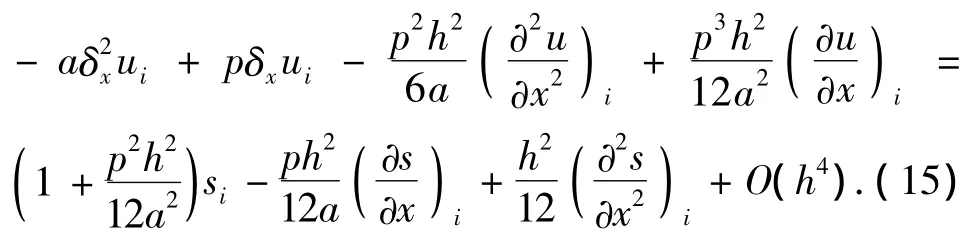
接着，将(5)式和(6)式代入(15)式，并利用(7)式和(8)式对u的1阶导数和2阶导数进行离散，整理可得

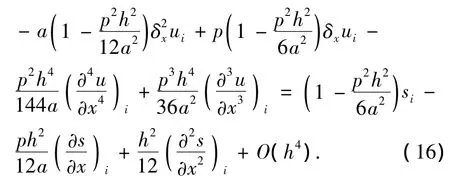
再将(10)式和(12)式代入(16)式，并利用(5)式和(6)式代替u的1阶导数项和2阶导数项，用(7)式和(8)式对u的1阶导数和2阶导数进行离散，整理可得

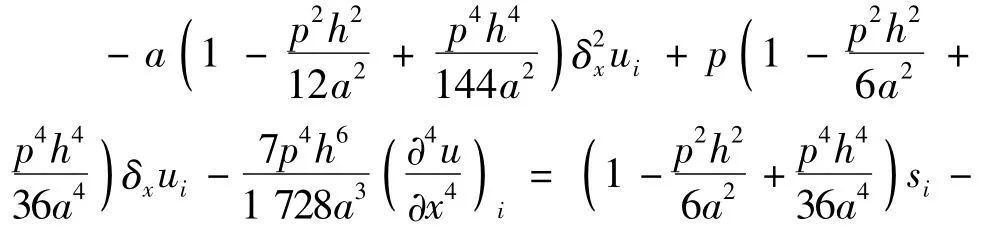
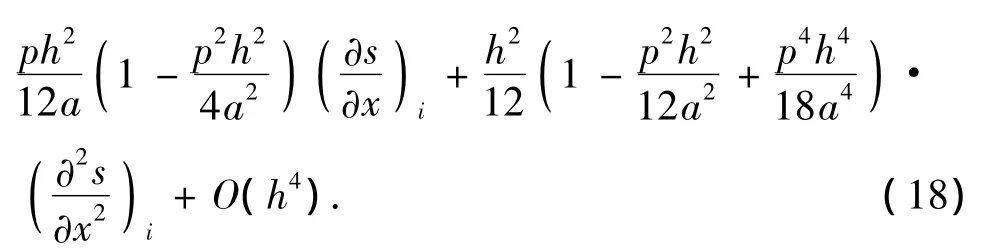
最后，将(18)式中s的1阶导数项和2阶导数项用中心差分近似，略去4阶导数项，化简整理可得(2)式的高阶紧致差分格式为

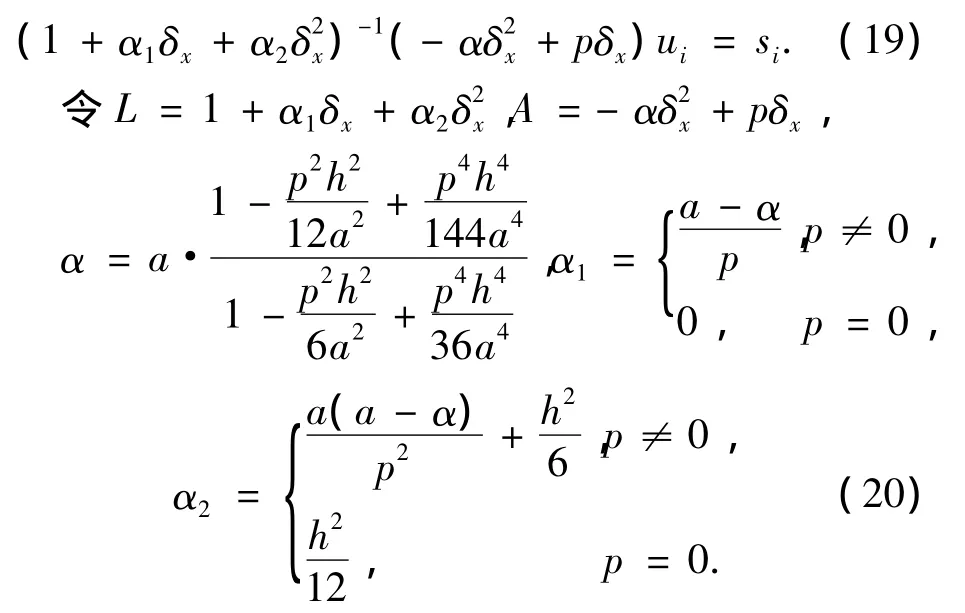
用(- ∂u∂)ti代替(19)式中的si，并且考虑方程在n+1/2时刻的值，则(19)式可以写为

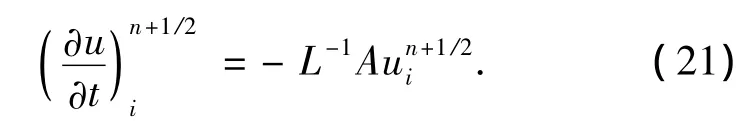
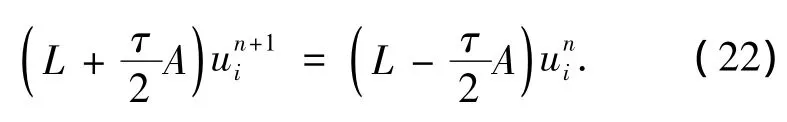
从推导过程可知，此格式的计算精度为O(h4)+O(τ2)，即此格式在空间上具有4阶精度，时间上具有2阶精度.

2 稳定性分析

下面采用von Neumann方法分析上述格式的稳定性.将数值解表示为Fourier级数的展开形式，其特征项为

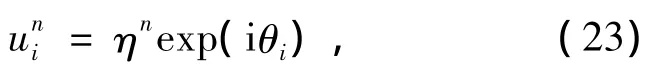
将(23)式代入(22)式得放大因子为

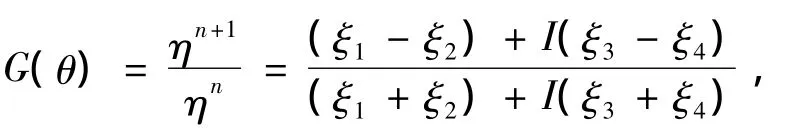
其中，ξ1=1-(4α2h2)sin2(θ 2)，ξ2=(2ατ h2)·sin2(θ 2)，ξ3=(α1h)sin θ，ξ4= ［pτ(2h)］sin θ，sin2(θ 2)∈［0，1］.所以

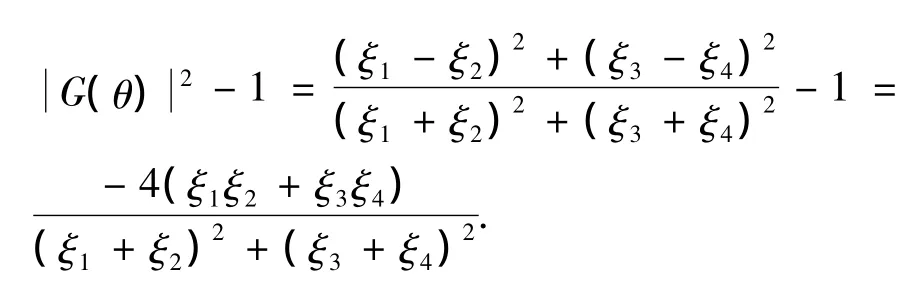
1)当p=0，a ＞0时，由(20)式可知，α=a，α1=0，α2=h212，所以

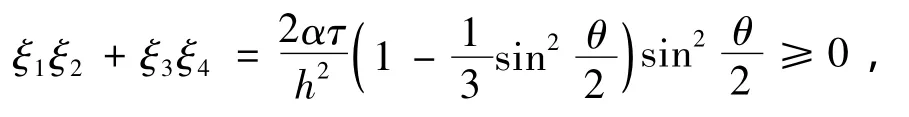
同理可证，2)当p≠0，a＞0时，3)当p≠0，a=0时，都有，即针对非定常对流扩散方程和非定常纯对流方程，本文格式均是无条件稳定的.

3 数值算例

为了验证本文格式的精确性和可靠性，对3个有精确解的非定常纯扩散问题、非定常对流扩散问题及非定常纯对流问题进行数值实验，并与Crank-Nicolson(C-N)格式和指数型高阶紧致(EHOC)格式［9］的计算结果进行比较.针对非定常纯扩散问题，本文格式与EHOC格式是同一格式，因此对于该问题，只给出了本文格式的计算结果.另外，需要说明的是，指数型高阶紧致(EHOC)格式不能被用于求解非定常纯对流问题.

例1 非定常纯扩散问题:

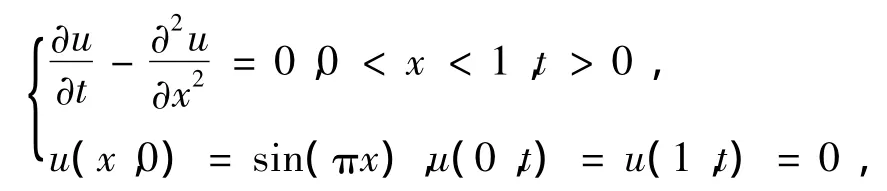
该问题的精确解为 u(x，t)=e-π2tsin(πx).

对于例1，表1给出了当τ=h2，T=1时，C-N格式与本文格式在不同空间步长下的最大绝对误差、2范数误差和收敛阶.从计算结果可以看出，本文格式在空间上具有4阶精度，而C-N格式只有2阶精度，并且随着空间步长的减小，本文格式的计算误差要比C-N格式减小得更快.表2给出当T=0.2时，针对不同的网格比r(τ=rh2)，采用C-N格式与本文格式计算的时间推进步数、最大绝对误差和2范数误差.可以看出，2种格式均是无条件稳定的.当取相同的τ和h时，本文格式的计算结果明显优于C-N格式;当取相同的h时，本文格式的计算误差随着τ的减小而减小，而C-N格式的计算误差随着τ的减小而增大.

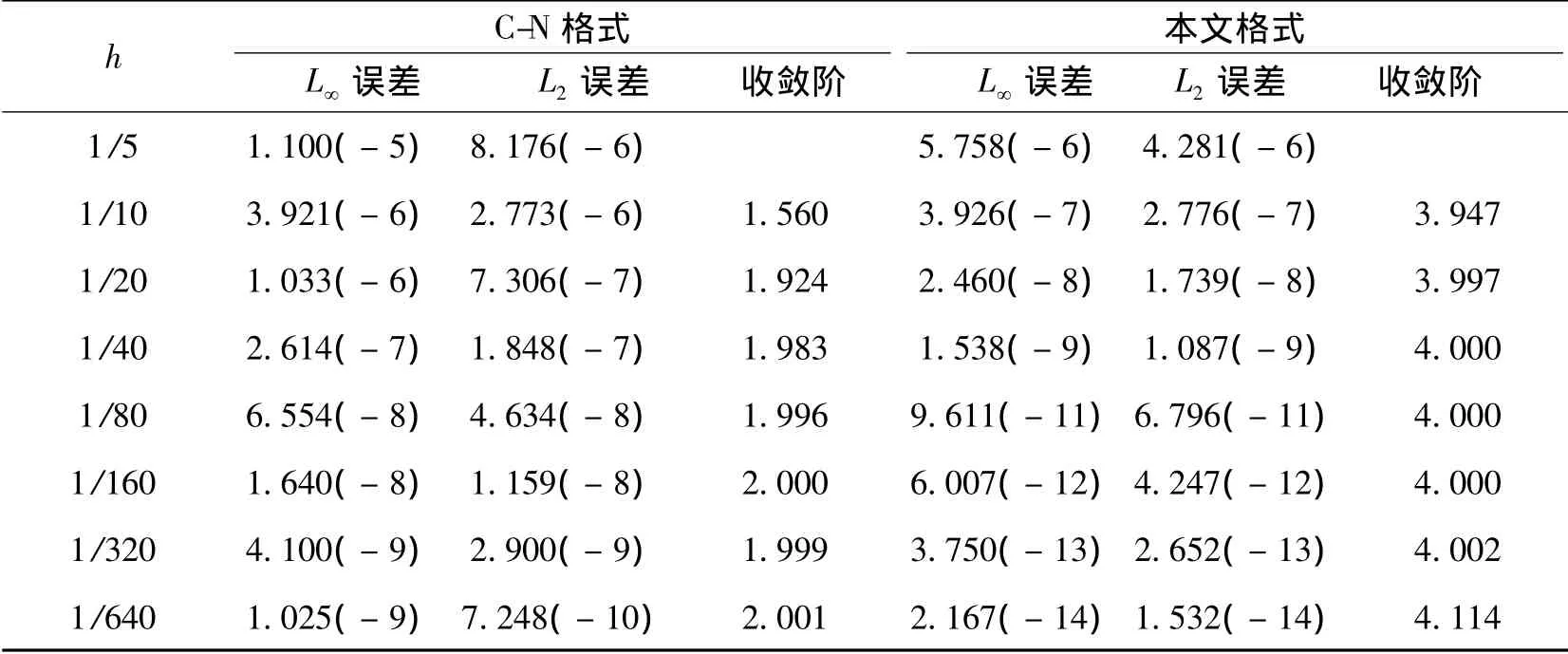
表1 当τ=h2，T=1时，C-N格式和本文格式的最大绝对误差、2范数误差及收敛阶

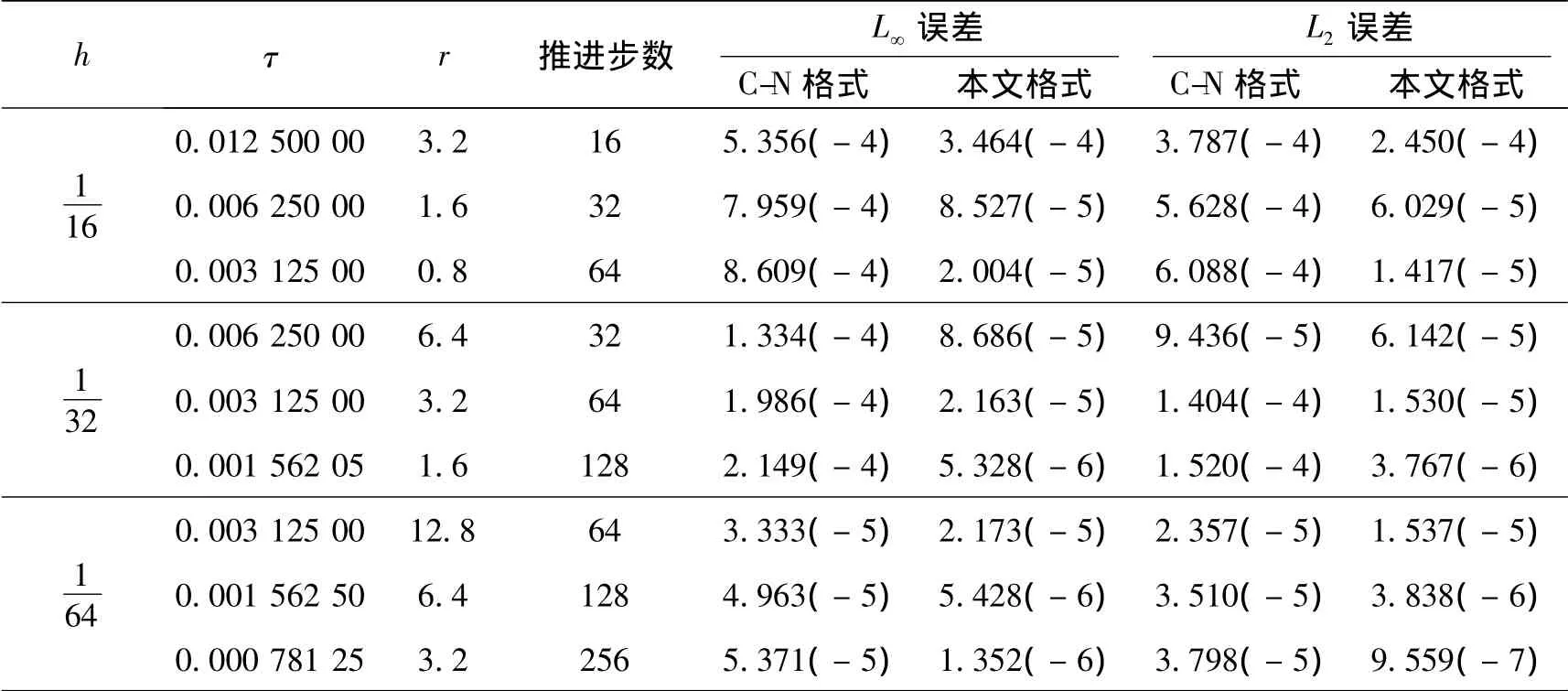
表2 当T=0.2时，C-N格式和本文格式的推进步数、最大绝对误差及2范数误差

例2 非定常对流扩散问题:

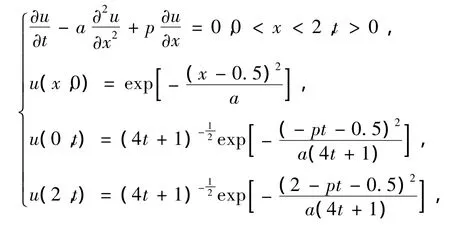
对于例2，表3给出了当a=0.01时，对不同的p、T、τ和 h，C-N 格式、EHOC 格式［9］及本文格式数值结果的最大绝对误差和2范数误差.可以看出，对于给定的p、T、τ和h，本文格式的计算误差要比C-N格式或EHOC格式更小.这充分表明了，针对1维非定常对流扩散问题，本文格式比C-N格式和EHOC格式具有更好的计算效果.

表3 C-N格式、EHOC格式及本文格式的最大绝对误差和2范数误差

表3 (续)

例3 非定常纯对流问题:

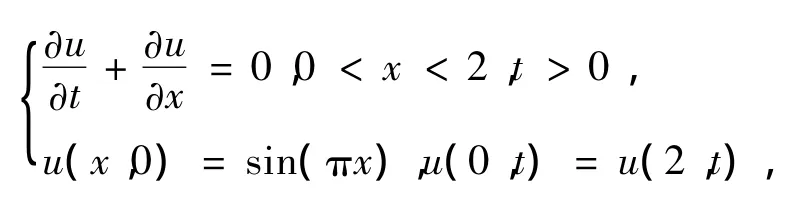
该问题的精确解为 u(x，t)=sin［π(x-t)］.

对于例3，表4给出了当τ=h2，T=1时，C-N格式与本文格式在不同空间步长下的最大绝对误差、2范数误差和收敛阶.计算结果表明，本文格式在空间上具有4阶精度，而C-N格式只有2阶精度，并且在相同空间步长下，本文格式的计算效果明显优于C-N格式.表5给出了当T=0.2时，针对不同的网格比r(τ=rh2)，计算的推进步数、最大绝对误差和2范数误差比较.可以看出，2种格式均是无条件稳定的.

表4 当τ=h2，T=1时，C-N格式与本文格式的最大绝对误差、2范数误差及收敛阶

表5 当τ=rh2，T=0.2时，C-N格式与本文格式的推进步数、最大绝对误差及2范数误差

4 结论

本文建立了1种求解1维非定常对流扩散方程的有理型高阶紧致差分格式，其空间具有4阶精度、时间具有2阶精度，并且采用von Neumann分析方法证明了该格式针对非定常纯扩散方程、非定常对流扩散方程及非定常纯对流方程均是无条件稳定的.最后通过数值实验，并与C-N格式和EHOC格式的计算结果进行比较，充分验证了本文方法的精确性和可靠性.

［1］刘扬.对流扩散方程的新型Crank-Nicholson差分格式［J］.数学杂志，2005，25(4):463-467.

［2］王同科.一维对流扩散方程Crank-Nicolson特征差分格式［J］.应用数学，2001，14(4):55-60.

［3］Gao Zhi.An infinite-order accurate upwind compact difference scheme for the convective-diffusion equati-on［C］∥Proceeding ofAsia Workshop on computational Fluid Dynamics.Chengdu:SichuanUniversity Press，1994:18-24.

［4］蔡国洋，田敏，冯秀芳.一类求解变系数对流扩散方程的指数型显式方法［J］.宁夏大学学报:自然科学版，2013，34(1):1-3.

［5］杨志峰，陈国谦.含源项非定常对流扩散问题紧致四阶差分格式 ［J］.科学通报，1993，38(2):113-116.

［6］林建国，许维德，陶尧森.含源项非定常非线性对流扩散方程的三次样条四阶差分格式［J］.水动力学研究与进展:A 辑，1994，9(2):599-602.

［7］Spotz W F，Carey G F.Extension of high-order compact schemes to time-dependent problems ［J］.Numerical Methods for Partial Differential Equations，2001，17(2):657-672.

［8］葛永斌，田振夫，吴文权.含源项非定常对流扩散方程的高精度紧致隐式差分方法［J］.水动力学研究与进展:A 辑，2006，21(5):619-625.

［9］田振夫.一维对流扩散方程的四阶精度有限差分方法［J］.宁夏大学学报:自然科学版，1995，16(1):32-35.

［10］Karaa S，Zhang Jun.High orderADImethod for solving unsteady convection-diffusion problems［J］.Journal of Computational Physics，2004，198(1):1-9.

［11］MacKinnon R J，Johnson R M.Differential equation based representation of truncation errors for accurate numerical simulation ［J］.International Journal for Numerical Methods in Fluids，1991，13(6):739-757.

［12］Spotz W F，Carey G F.High-order compact scheme for the steady stream-function vorticity equations［J］.International Journal for Numerical Methods in Engineering，1995，38(3):3497-3512.

［13］You D.A High order PadéADImethod for unsteady convection-diffusion equations［J］.Journal of Computational Physics，2006，214(1):1-11.