项目属性标错时可达阵补救作用的研究

甘朝红，汪文义，丁树良

(江西师范大学计算机信息工程学院，江西南昌330022)

0 引言和记号

在认知诊断过程中，题目属性的标定非常重要，即Q矩阵的标定非常重要［1-2］.当题目属性标定出现差错时，可能导致属性层级关系的混乱，且属性标定出现差错在所难免.为了提高认知诊断的准确率，应尽量避免差错，或设计当出错时可以弥补这些差错的预案.

当题目属性标定出现错误时，有研究［3-5］讨论了如何修正Q矩阵.本文和以往研究问题的角度不同，不是去修改Q阵，而是建立弥补的预案.已有理论和实验中表明，可达阵R在认知诊断测验编制中起着重要作用［6］.受此启发，本文用Matlab作为程序设计语言编程进行模拟实验，研究可达阵R对项目属性标定出错后是否有补救作用.本文从分析专家给测验项目标定属性时，可能出现的差错入手，研究设计不同的测验Q矩阵对题目属性标定出现差错的容忍能力.用R表示可达矩阵，Qt表示测验Q矩阵，即测验蓝图［7］.基于可达矩阵R通过扩张算法［10］得到的矩阵称为潜在 Q 矩阵［8-9］，记为Qp.

设欲诊断的问题包含n个属性，将把穷举n个属性的所有0-1列得Qall，Qall的列数为2n;记不符合属性层级关系的列构成的矩阵为Qcuo，从Qall的2n列中去掉0列，再去掉Qp的所有列，即构成错误列矩阵Qcuo;而在Qp矩阵中由可达阵R扩张出的列称为扩张矩阵，记为Qkuo.考虑2类包含错误标定题目属性的Qt:1)Qt含可达阵;2)Qt不含可达阵.测验项目标定属性时可能出现的差错，不外乎以下2种情况:(i)在专家标注的Qt中，有题目属性层级关系出错，这种错误在属性层级关系紧密时却假设其是独立结构时容易发生;(ii)专家标定的Qt的列虽然符合属性层级关系，但出现了误指，即Qt中的第j列应为 qj，但专家错标为 qi，qj≠qi，而 qj和 qi均为Qp中的列.

本文按以上2种差错情况进行实验，前提假设是专家界定的属性及其层级关系正确，只是在对具体测验项目标定属性及其层级关系时出错.

1 研究思路和研究方法

由于认知诊断测验蓝图的设计中可达矩阵有重要作用［6］，因此在研究中分别设计项目数相同和错误列数相同的测验矩阵Qt，又分为包含整个可达阵、仅仅包含可达阵某些列以及不包含可达阵任何列的情况进行比较，考察可达阵是否能够减轻其他项目属性标注不准确引起的不良后果.再考虑错误的列数不同情况，分别就属性层级关系类型的不同进行一一比较.

考虑5种基本属性层级关系(线型、收敛型、发散型、无结构型和独立型)，设置不同的Qt，通过插入或者取代可达阵的若干列对诊断准确率的差异来验证可达阵对Qt出现错误的弥补作用.以下考虑5个属性，且属性及其层级关系见图1.

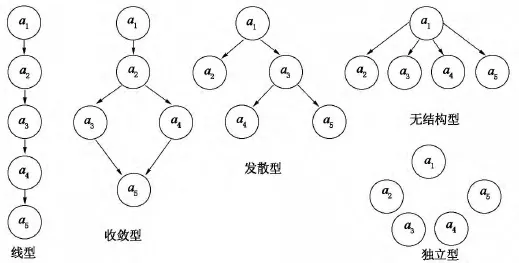
图1 属性及其层级关系图

以下实验以DINA模型［11-14］为认知诊断模型，模拟失误和猜测参数(服从［0.05，0.25］上的均匀分布).在每一个条件下模拟1000个被试，重复做多次实验求模式判准率的平均值进行比较.整个实验过程均用Matlab语言编程实现.

2 出现第1种差错的实验及结果分析

2.1 实验设计

出现第1种差错情况下，设计3类测验矩阵Qt:(Ⅰ)Qt中均为Qcuo中随机抽取的列;(Ⅱ)随机抽取 Qkuo中的1，2，3，…列逐步取代(Ⅰ)中 Qt的第1，2，3，…列;(Ⅲ)用可达阵 R 中的1，2，3，…列逐步取代(Ⅰ)中Qt的第1，2，3，… 列，并且在同一次实验中(Ⅰ)、(Ⅱ)和(Ⅲ)相对固定.比较3类测验矩阵下的模式判准率，如果情况(Ⅲ)的模式判准率高于(Ⅰ)和(Ⅱ)，说明可达阵对项目属性标定出错后有补救作用.由于试验中存在随机行为，为减少实验误差，采用重复实验30次取判准率的平均值进行比较，并且求其均方差以了解各次实验结果的变动程度.

考虑到以下2种情况:1)在线型结构中，Qp=R，即在该层级关系下Qkuo有0列，因而无法构造出不含可达阵的列，从而也就无法反衬出可达阵的弥补作用，所以这里不讨论线型结构;2)在独立结构中，Qp有2n-1列，属性与属性之间没有先决关系，也就无法构造不符合属性层级关系的错误列，所以独立结构在第1种情况下不需要讨论.因此，对发生了第1种属性标错的情况，只讨论收敛型、发散型和无结构型3种层级关系下的各种情况.

2.2 实验结果及分析

2.2.1 收敛型实验结果及分析 由图1和扩张算法，可知Qp有6列，Qkuo只有1列，Qcuo为25列，根据上述方法构造的测验Qt有8种，记为Qt(k)，k=1，2，…，8，其中 Qt(1):从 Qcuo的 25 列随机选 6 列;用Qkuo的1列随机取代Qt(1)的1列，得Qt(2);用R的h列随机取代Qt(1)的h列，得到Qt(2+h)，h=1，2，3，4，5;Qt(8):用 Qp做测验项目矩阵.

表1为在收敛型结构下，上述8个测验项目矩阵分别实验30次时的平均模式判准率和均方差.以表1中平均值为数据绘制折线图为图2中带菱形节点的折线.

表1 收敛型结构下的平均判准率和均方差

在表1中，测验矩阵Qt(1)均由属性层级关系有误的列构成时，平均判准率较低，当以扩展列取代其中1列后，平均判准率有所提升，随着Qt中可达阵列数的增加，其平均判准率不断上升，图2中带菱形节点的折线也清楚地表明这一点.特别地，从表1中Qt(2)和Qt(3)看，Qt(3)的平均判准率更高，说明测验矩阵中其他相同的情况下，含可达阵列的比含扩展列的平均判准率要高.即当出现第1种差错的情况时，测验项目中包含可达阵的的模式判准率比测验项目中不包含或不完全包含可达阵的模式判准率更高.均方差表明各次实验结果的波动差异性不大.

2.2.2 发散型实验结果 由图1和扩张算法，可知Qp有10列，则 Qkuo有5列，Qcuo的列数为21列，根据上述方法构造的Qt有12种，记为 Qt(k)，k=1，2，…，12.其中Qt(1):从 Qcuo的21列随机选7列;用Qkuo的h列随机取代Qt(1)的h列，得Qt(1+h)，h=1，2，3，4，5;用 R 的 h 列随机取代 Qt(1)的 h 列，得到 Qt(6+h)，h=1，2，3，4，5;Qt(12):用 Qp作 Qt.实验结果如表2所示，以表2中平均值为数据绘制折线图为图2中带矩形节点的折线.

表2 发散型结构下平均判准率和均方差

比较表2中的平均值，其中Qt(7)＞Qt(2)，Qt(8)＞Qt(3)，Qt(9)＞ Qt(4)，Qt(10)＞Qt(5)，Qt(11)＞Qt(6)，说明相同情况下扩展列的弥补作用不如可达阵列的，而且用可达阵的第1列，2列，…去替换，图2中带矩形节点的折线上扬，表明平均判准率呈上升趋势，可见可达阵的弥补作用明显.均方差结果表明各次实验结果的差异性不大.

2.2.3无结构实验结果 由图1和扩张算法，可知Qp有16列，则Qkuo有11列，Qcuo的列数为15列，根据上述方法构造的Qt有12种，记为Qt(k)，k=1，2，…，12，其中 Qt(1):从 Qcuo的15列随机选7列;而从Qt(2)到Qt(12)的定义和发散型中相同.实验结果如表3所示，以表3中平均值为数据绘制折线图为图2中带三角形节点的折线.

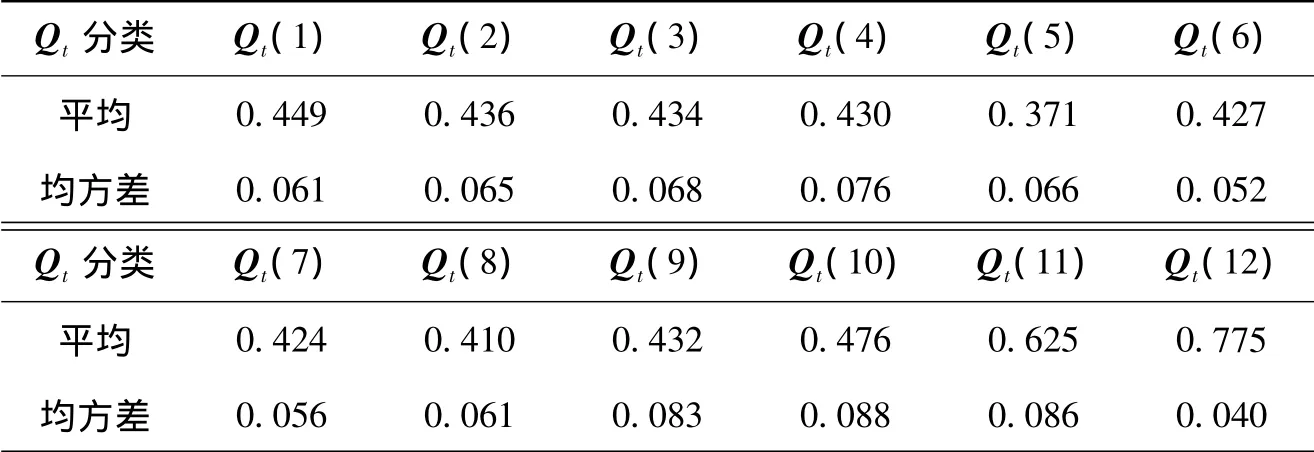
表3 无结构平均判准率和均方差

图2 发生第1种差错下Qt不同时平均判准率比较

从表4、表5和图2中带三角形节点的折线看出，属性层级关系有误的列作测验项目矩阵的情况下，平均判准率较低，说明出现这种差错会导致判准率下降，用扩展列去替换其弥补作用不明显，而用可达阵的列替换，开始不明显，当达到4列以上，其弥补作用就比较明显.均方差结果表明各次实验结果的差异性不大.

综上可见:当出现第1种差错的情况时，测验项目中包含可达阵的模式判准率比测验项目中不包含或不完全包含可达阵的模式判准率更高.

3 出现第2种差错的实验及结果分析

3.1 实验设计

出现第2种差错时，测验项目矩阵Qt中的第j列应为qj，但错标为qi，其中i≠j.而qj和qi都是简化关联矩阵Qp中的列.显然被试仍然按qj作答，而期望反应模式的计算却以qi为准，这必造成误判，使得判准率不高.为了验证可达阵是否对错误列造成的判准率下降有弥补作用，以可达矩阵R为基础，分别添加qj或者qi，其中添加qj的测验矩阵记为 Qto，添加qi的测验矩阵记为Qt.先求基于Qto的模式判准率PMR5，而后从扩展矩阵Qkuo中抽取h列，分别取代上述Qto和Qt中可达矩阵R部分的h列，h=1，2，…，5，求各种取代后的模式判准率记为PMR4、PMR3、PMR2、PMR1和 PMR0.观察 6 种情况下判准率的变化，随着Qto中可达矩阵R部分中的列数减少，如果判准率呈下降趋势的话，说明可达阵对出现的差错有弥补作用.

特别地，为了保证实验的完备性，首先，qj和qi应该在简化关联矩阵Qp随机取不同的2列;其次用来取代Qto和Qt的R中的列应该在Qkuo中随机选取.因此，应该实验多次求其平均进行比较.

具体而言，实验设计如下:1)从简化关联矩阵Qp随机取出不同的2列作为qj和qi;2)令Qt=［R|qi］，Qto=［R|qj］，求模式判准率 PMR5;3)从 Qkuo中随机取1列取代2)中Qto和Qt的R中的1列，求模式判准率 PMR5-h;h=1，2，3，4，5;4)重复以上各步骤 100 次，分别求 PMR5、PMR4、PMR3、PMR2、PMR1和PMR0的平均值进行比较.

3.2 实验及结果分析

从图1的各种层级关系的可达阵和简化关联矩阵来看，线型结构没有扩张列，收敛型结构扩张列只有1列，无法按上面的实验设计思路进行实验，可以采用其他方法实验(比如采用逐渐增加可达阵的个数)，对此本文不讨论，而只讨论发散型、无结构型和独立型3种结构.

对上述6种情况，每种做100次实验.第2种差错下，3种结构下平均判准率的实验结果如表4所示，以表4为数据生成图，如图3所示.

表4 发生第2种差错时模式判准率比较(100次实验的平均值)

图3 发生第2种差错下平均判准率比较

从表4和图3看出，在用扩张列替代可达阵的过程中，随着扩张列数增加，可达阵的列数随之减少，3种结构下判准率都呈下降趋势.说明5个属性，错1列的情况下，对项目标定出现第2种差错时，含可达阵列数越多其弥补作用越明显.

3.3 进一步验证

假定测验项目矩阵Qt中的第j列本来应该是qj，但错标为qi，设计4类Qt以进一步验证可达阵对其他项目中属性错误标定的补求作用:1)可达阵之外再加上未标错属性的1列;2)可达阵之外再加上标错属性的1列;3)扩张部分5列再加上未标错属性的1列;4)扩张部分5列再加上标错属性的1列.对上述4类Qt分别实验求模式判准率，对应地记为 PMR1、PMR2、PMR3和 PMR4.定义 1 次差值为D1和 D2，其中 D1=PMR1-PMR2，D2=PMR3-PMR4.D1和D2分别表达可达矩阵和非可达矩阵(即扩张部分)对于其他题目的属性的错误标定的补偿作用.考虑到对试验结果的预期是可达矩阵对其他题目属性的错误标定有比较大的补偿功能，所以D1的值应该比较小，因此再定义2次差值为D，其中D=D2-D1.如果D＞0，则说明可达矩阵对于其他题目属性的错误标定有补偿功能.

实验只考虑发散型结构、无结构型和独立结构3种类型，原因同上述.以DINA模型为认知诊断模型，模拟1000被试，模拟失误和猜测参数，对上述4种Qt分别做实验，每次实验从简化关联矩阵Qp随机取出不同的2列作为qj和qi，从Qkuo中随机取5列取代可达阵构造不同的Qt，一次实验求得4个模式判准率 PMR1、PMR2、PMR3和 PMR4，继而求出模式判准率的差值D1和D2，重复实验100次求100个差值的平均.整个实验过程均用Matlab语言编程实现.实验结果如表5所示.

表5 3种结构下1次差值和2次差值(100次实验的平均值)

由表5看出，3种结构下，D1和D2的值均大于0，说明在给项目标注属性时，标错属性会导致模式判准率降低;而每种结构下D大于0，即D1小于D2，说明测验矩阵中含可达阵时，属性标错时的判准率更接近正确标注时的判准率.可见可达阵在项目属性标注出错时确有弥补作用.

4 结论和展望

通过对5个属性，5种属性层级关系结构的模拟实验得出:测验项目中包含可达阵的模式判准率比测验项目中不包含或不完全包含可达阵的模式判准率更高，而且可达阵对其他项目属性标定中出现的差错有一定的补救作用.这进一步验证了可达阵的在测验编制中的重要作用.如果在测验项目矩阵中加入可达阵，使各种知识状态对应不同的理想反应模式，哪怕其他项目质量稍差一些，都可以最大限度地提高诊断准确率.这表明在实际工作中，命题专家对于可达阵的列对应的题目应该精雕细刻，因为它们可以使Qt有一定的稳健性.

［1］ Tatsuoka K K.Rule space:an approach for dealing withmisconceptions based on item response theory［J］.Journal of Educational Measurement，1983，20(4):345-354.

［2］丁树良，汪文义，罗芬.认知诊断中Q矩阵和Q矩阵理论［J］.江西师范大学学报:自然科学版，2012，36(5):441-445.

［3］Leighton J P，Gierl M J.Cognitive diagnostic assessment for education:theory and applications［M］.Cambridge:CambridgeUniversity Press，2007:242-274.

［4］de la Torre J.An empirically basedmethod of Q-matrix validation for the DINAmodel:Development and applications［J］.Journal of Educational Measurement，2008，45(4):346-362.

［5］涂冬波，蔡艳，戴海琦.基于DINA模型的Q矩阵修正方法［J］.心理学报，2012，44(4):558-568.

［6］丁树良，杨淑群，汪文义.可达矩阵在认知诊断测验编制中的重要作用［J］.江西师范大学学报:自然科学版，2010，34(5):490-494.

［7］丁树良，汪文义，杨淑群.认知诊断测验蓝图的设计［J］.心理科学，2011，34(2):258-265.

［8］祝玉芳，丁树良.规则空间模型理论基础的改进［J］.江西师范大学学报:自然科学版，2008，32(1):69-72.

［9］丁树良，祝玉芳，林海菁，等.Tatsuoka Q矩阵理论的修正 ［J］.心理学报，2009，41(2):175-181.

［10］杨淑群，蔡声镇，丁树良，等.求解简化Q矩阵的扩张算法［J］.兰州大学学报:自然科学版，2008，44(3):87-91，96.

［11］RuppAA，Templin J.The effects of Q-matrixmisspecification on parameter estimates and classification accuracy in the DINAmodel［J］.Educational and Psychological Measurement，2008，68(1):78-96.

［12］de la Torre J.DINAmodel and parameter estimation:a didactic［J］.Journal of Educational and Behavioral Statistics，2009，34(1):115-130.

［13］丁树良，汪文义，罗芬.多级评分认知诊断测验蓝图的设计:根树型结构［J］.江西师范大学学报:自然科学版，2014，38(2):111-118.

［14］丁树良，罗芬，汪文义.多级评分认知诊断测验蓝图的设计:独立型和收敛型结构［J］.江西师范大学学报:自然科学版，2014，38(3):265-269.