基于模型函数与L-曲线的正则化参数选取方法

胡 彬，徐会林，王泽文，喻建华

(东华理工大学理学院，江西南昌330013;2.河南理工大学数学与信息科学学院，河南焦作454000)

0 引言

反问题研究已是计算数学及应用数学领域研究的热点问题之一.反问题一般是不适定的［1］，其不适定性在数值计算上表现为解不连续依赖测量数据.即使在实际测量过程中测量误差非常小，也会引起解的巨大波动.目前求解不适定问题最具有普遍性、完备性的是Tikhonov正则化方法，但该方法的有效性取决于选取到合适的正则化参数.目前比较有代表性的正则化参数选取策略有:Morozov偏差原理、广义交叉检验、L-曲线(L-curve)等准则.当误差水平已知或可估计时，Morozov偏差原理是最常采用的正则化参数选取策略之一，但是当不适定算子方程右端项的误差水平δ未知时，Morozov偏差原理就失效了.为了克服Morozov偏差原理需要已知误差水平的局限性，P.C.Hansen等提出基于L-曲线的正则化参数选取方法［2-3］，可以在误差水平未知的情形下找到近似最佳的正则化参数.

在利用Morozov偏差原理确定正则化参数时需要借助牛顿迭代，而牛顿迭代的计算量比较大，为了克服这一缺点，文献［4-7］中提出了1种新的确定正则化参数的方法—模型函数法.它是将Tikhonov泛函定义为关于α的函数，再用1个简单的具有显示表达式的模型函数来近似F(α)，通过简单迭代确定正则化参数.

本文在上述2种方法的基础上研究了基于模型函数的修正L-曲线准则，证明了所得序列点是局部收敛的，给出了相应的迭代算法.通过算例验证了该准则的有效性，同时也指出了目前还存在的不足和今后进一步研究的方向.

1 模型函数法

线性反问题一般可归结为解第1类不适定算子方程:

其中K是Hilbert空间X到Y上的有界线性算子.由于观测数据存在误差，所以一般把方程(1)改写为

其中δ为误差水平，‖yδ-y‖≤δ.Tikhonov正则化方法是将求不适定方程(2)的解转为求Tikhonov泛函

的最优解，其中α＞0是正则化参数.对于固定的正则化参数α，记最优函数为

引理1［4］设K:X→Y是有界线性算子，X，Y均为Hilbert空间.∀α ＞0，(3)式的唯一解x(α)是无穷次可微的，且g=dnx(α)dαn∈X可由

递推求解得到.

定理1［4-5］最优函数F(α)在(0，+∞)内是无限次可微的，且∀α ＞0，F(α)满足

模型函数的方法就是在αk附近构造F(α)的局部近似函数Fk(α)，使其满足微分方程(4)，即

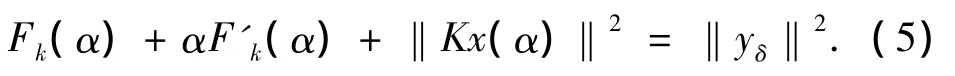
若假设‖Kx(α)‖2≈ Tk‖x(α)‖2，代入(5)式并注意到 F'(α)= ‖x(α)‖2，解得

即得到双曲模型函数:

由于 Kx(α)≈ yδ，故可设 ‖Kx(α)‖2≈‖yδ‖2-Tk，代入(5)式得

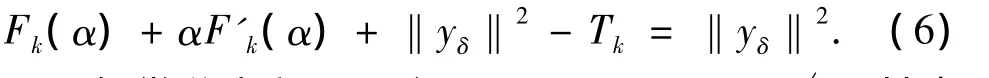
解微分方程(6)，得Fk(α)=Tk+Ckα，其中Ck、Tk是待定参数且由方程组

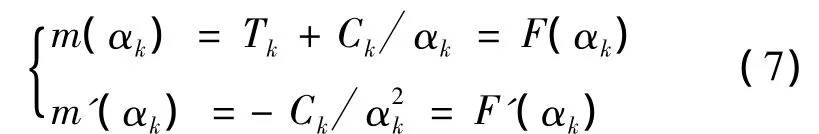
确定，即

于是，得到更为简洁的双曲模型函数:

文献［8］研究了非精确数据下的线性模型函数选取正则化参数.虽然线性模型函数具有计算简单、收敛性较好等优点，但是却不能将它与L-曲线准则相结合而得到选取正则化参数的算法.文献［9］将双曲模型函数m1(α)应用于L-曲线选取准则获得选取正则化参数的新算法.本文是前述研究的继续和深入，基于双曲模型函数m2(α)研究修正的L-曲线选取准则，从而获得选取正则化参数选取的新方法.

2 修正的L-曲线准则

L-曲线准则是残差‖Kx(α)-yδ‖2与正则化解‖x(α)‖2在一组正则化参数下所构成的图像，也就是由(‖Kx(α)-yδ‖2，‖x(α)‖2)所构成的平面曲线.最优的正则化参数α出现在曲线的拐点处. 通常转化为对应的(2log‖Kx(α)-yδ‖，2log‖x(α)‖)曲线，因为曲线形状如字母L(见图1)，故称为L-曲线准则.从图像上很容易找到曲线的拐点，即最优正则化参数α在对应曲线的“角点”出现.记u(α)=2log‖Kx(α)-yδ‖，v(α)=2log‖x(α)‖，则L曲线上各点的曲率公式［10-11］为

曲率最大的点对应正则化参数即为所需正则化参数.

图1 L-曲线示意图

由文献［12］知，若L-曲线在点α=α*处取到最大曲率，且在该点处曲线的斜率为 -1/μ，则下列泛函:

在α=α*处取得极小值.因此，选取正则化参数的L-曲线准则等价为求泛函(8)的极小值点.修正的L-曲线准则就是通过求(8)的极小值来获得合适的正则化参数.由于是α的非线性隐式函数，不便于计算.本文利用模型函数的方法将(8)式显化，从而简化计算，提高计算效率.

3 基于模型函数的修正L-曲线算法

对于任意给定的α＞0，最优函数F(α)为

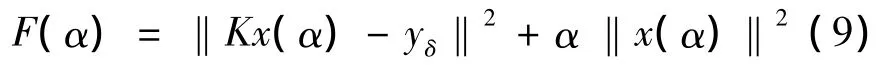
且F'(α)= ‖x(α)‖2，则(8)式可改写成F(α)的形式，即

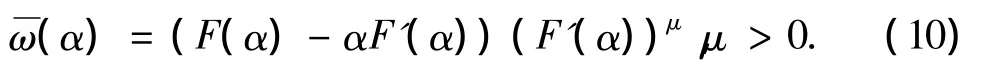
模型函数m(α)是F(α)的局部近似，则(9)式的局部近似为

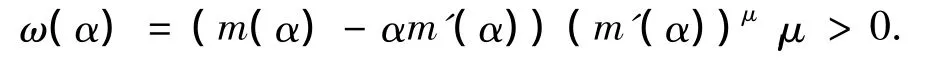
本文主要研究了双曲模型函数m2(α)，代入(10)式得 ω(α)=(T+2C/α)(-C/α2)μ.

对 ω(α)求导，得

令 ω'(α)=0，解得 α=-C(1+2μ)(μT).

对于正则化参数 αk，求得对应的正则化解x(αk)，再根据方程组(7)可确定参数 Ck，Tk，则

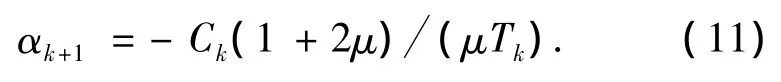
由(11)式及Ck＜0，Tk＞0知αk+1＞0且它是唯一的.该算法比文献［9］中的更为简单，因为文献［9］给出的是关于α的2次方程，选取其中较大的作为正则化参数αk+1.

综合上面分析，得到基于双曲模型函数m2(α)与修正的L-曲线正则化参数选取策略的新算法:

算法1 给定 ε ＞ 0，yδ，K，μ ＞ 0;

Step 1 给定1个初始值α0＞α*，置k=0;

Step 2 解正则化方程αkx+K*Kx=Kyδ;

Step 3 求出 Ck，Tk，αk+1;

Step 5 停止迭代，输出正则化参数αk+1.

定理2 如果

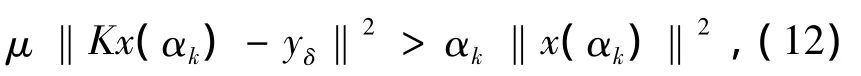
则在算法1中函数ωk(α)在点αk处是局部严格单调递减的.

证算法1中产生的函数ωk(α)为

ωk(α)=(Tk+2Ck/α)(-Ck/α2)μ，则 ωk'(α)=(-Ck)μ(-2Ck+(αTk+2Ck)·(-2μ))/α2μ+2.取 α= αk，把(7)式中解得 Ck，Tk的表达式代入得

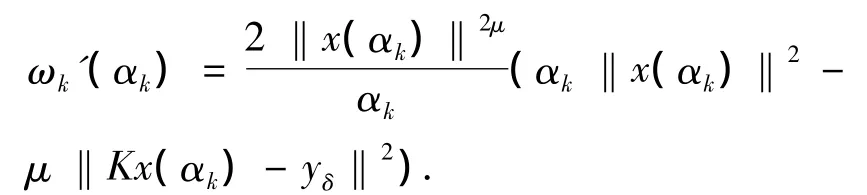
由已知条件得ω'k(αk)＜0，即函数ωk(α)在点αk处是局部严格单调递减的.

定理3 给定初始值α0满足(12)式，则算法1产生严格单调递减序列{αk}且收敛.

证由定理2 的证明过程知，

令 φ(α)=-2Ck+(αTk+2Ck)(-2μ)，显然φ(αk)＜ 0，φ'(αk)＜ 0.所以函数φ(α)是严格单调递减的.由算法1知φ(αk+1)=0，所以αk＞ αk+1.又∀k均有αk＞0，故收敛性成立.

4 数值算例

例1 求解第1类Fredholm积分方程［13］:

其中，核 K(s，t)=1 ［1+100(t-s)2］，

本文用等距节点复化梯形公式来离散第1类Fredholm 积分方程(13)，得线性方程组Ax－=y－，其中把积分核K(s，t)离散成矩阵Am×n，x(s)离散成n维列向量x－.对方程组右端加入随机扰动为

其中r为Matlab中的随机函数.取不同的误差值δ，求出对应不同误差值δ的正则化参数，并把不同正则化参数求出的正则化解对比(见图2～4)，其中实线表示无扰动下的精确解，星形线表示不同正则化参数下的数值近似解.

情形1 当δ=5.8378e-4，α=3.7320e-4，正则化解的相对误差ρ=0.0678.正则化解与真解如图2和图3所示，其中图2是该情形下未作正则化处理的计算所得解(即当α=0时的最小二乘解)，图3为算法1计算所得解.

情形2 当δ=8.5401e-8，α=6.6470 e-4，正则化解的相对误差ρ=0.0500，算法1计算结果如图4所示.

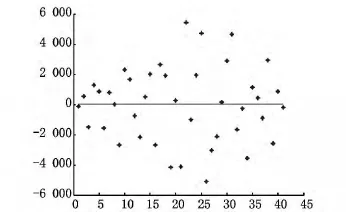
图2 α=0

图3 α=3.7320e-4

图4 α=6.6470e-4

例2 求解第1类Fredholm积分方程［14-15］:

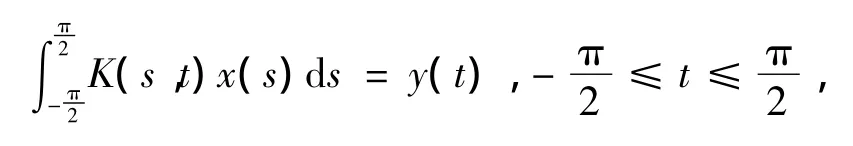
x(s)=a1e-c1(s-t1)2+a2e-c2(s-t2)2，a1=2，a2=1，c1=6，c2=2，t1=0.8，t2=-0.5，K(s，t)=(cos(s)+cos(t))2(sin(u)u)，u= πsin(s).

情形1 当δ=0.0022，α=0.0470时，正则化解的相对误差ρ=0.1746.正则化解与真解如图5和图6所示，其中图5是未作正则化处理的计算所得解，图6为算法1计算所得解.

图5 α=0

图6 α=0.0470

情形2 当δ=2.2268e-5，α=0.0466时，正则化解的相对误差ρ=0.1744，算法1计算结果如图7所示.

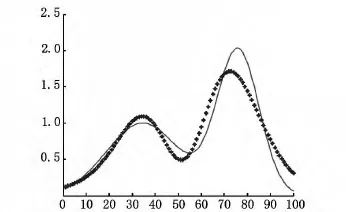
图7 α=0.0466

5 结论

本文基于模型函数方法研究了正则化参数选取的修正L-曲线准则，使得计算上更加简单.从算例的模拟结果可以看出，基于双曲模型函数m2(α)的所得修正后的L-曲线准则是有效的.但是，本文只证明了初始正则化参数选取满足一定前提条件下，算法1产生的序列是局部收敛的.对于是否存在全局收敛性的算法［16］，还有μ值选取原则等问题还需进一步研究.

［1］刘继军.不适定问题的正则化方法及应用［M］.北京:科学出版社，2005.

［2］Hansen P C，O’Leary D P.The use of the L-curve in the regularization of discrete ill-posed problems［J］.SIAM J Sci Comput，1993，14(6):1487-1503.

［3］ Hansen P C.Analysis of discrete ill-posed problems bymeans of the L-curve ［J］.SIAM Review，1992，34(4):561-580.

［4］Xie Jianli，Zou Jun.An improvedmodel functionmethod for choosing regularization parameters in linear inverse problems［J］.Inverse Problems，2002，18(5):631-643.

［5］王泽文，徐定华.线性不适定问题中选取Tikhonov正则化参数的线性模型函数方法［J］.工程数学学报，2013，30(3):451-466.

［6］Wang Zewen，Liu Jijun.Newmodel functionmethods for determining regularization parameters in linear inverse problems［J］.Applied Numerical Mathematics，2009，59(10):2489-2506.

［7］Wang Zewen.Multi-parameter Tiknonov regularization andmodel function approach to the damped Morozov principle for choosing regularization parameters［J］.Journal of Computational andApplied Mathematics.2012，236(7):1815-1832.

［8］胡彬，夏赟，喻建华.算子非精确条件下确定正则化参数的一种方法［J］，江西师范大学学报:自然科学版，2014，38(1):65-69.

［9］Heng Yi，Lu Shuai，MhamdiA，et al.Model functions in themodified L-curvemethod-case study:the heat flux reconstruction in pool boiling［J］.Inverse Problems，2010，26(5):1-13.

［10］张立涛，李兆霞，张宇峰，等.结构识别计算中基于L-曲线的模型确认方法研究［J］.运动与冲击刊，2011，30(11):36-41.

［11］王宏志，赵爽，胡艳君.基于L-曲线正则化的MAP超分辨率图像复原［J］.吉林大学学报:理学版，2008，46(2):275-278.

［12］ Reginska T.A regularization parameter in discrete illposed problems［J］.SIAM J Sci Comput，1996，17(3):740-749.

［13］樊树芳，马青华，王彦飞.算子及观测数据都非精确情况下一种新的正则化参数选择方法［J］.北京师范大学学报:自然科学版，2006，42(1):25-31.

［14］王彦飞.反问题的计算方法及应用［M］.北京:高等教育出版社，2007.

［15］郭文彬.奇异值分解及其广义逆理论中的应用［M］.北京:中国科学院研究生院，2003.

［16］高炜，朱林立，梁立.基于图正则化模型的本体映射算法［J］.西南大学学报:自然科学版，2012，34(3):118-121.