单矢量水听器改进MUSIC算法的噪声抑制性能研究＊

张 炜 程锦房 房俊伟

（海军工程大学兵器工程系1） 武汉 430033） （海军装备研究院系统所2） 北京 100161）（中国人民解放军91183部队3） 青岛 266044）

0 引 言

实际海洋环境噪声场有各向同性的非相干噪声、相干噪声、部分相干和部分非相干噪声等3类．多数情况下，相干噪声是主要的背景噪声之一．舰船自噪声有重要的相干分量，当海况较高时，海洋动力噪声也含有重要的相干分量［1－3］；多目标检测时，强目标声辐射是检测弱目标信号时的相干噪声，研究相干噪声背景下的目标方位估计更具有实际的工程意义．

以往的矢量水听器的子空间分解类算法（如MUSIC算法）都是以各向同性（非相干）噪声场作为假设条件的［4］．而入射信号相关程度的强弱直接影响基阵协方差矩阵的结构，相干噪声可能使协方差矩阵变成病态矩阵，从而影响信号子空间和噪声子空间的正确划分及信号、噪声特征向量的正确估计，并使算法性能变差．

本文将阵列信号处理的空时相关矩阵算法［5］用于单矢量水听器目标方位估计，提出了单矢量空时相关矩阵MUSIC算法，仿真实验表明不论噪声相关性的强弱，新算法的噪声抑制能力和目标分辨能力均优于原方法．

1 矢量水听器信号模型

假设信号以平面波形式入射到水听器上，以二维矢量水听器为例，输出同点的声压p（t）和正交的二维振vx（t），vy（t），ρ0c＝1，考虑到环境噪声场影响，则单矢量水听器的数据模型可以表示为［6］

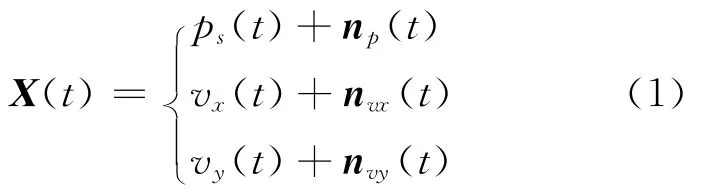
式中：np（t），nvx（t）和nvy（t）为1×n维噪声矩阵，且S（t）＝［p（t），vx（t），vy（t）］T为信号矩阵．则采样产生一个3×N维的矢量水听器阵列矩阵X（t），N 是数据采样点数，此时A（θ）为3×N 维的流型矩阵，其表达式为

式中：a（θk）＝［1，cosθk，sinθk］T为第k个信号的单矢量水听器阵列流型，则单矢量水听器接收数据X（t）的协方差矩阵：

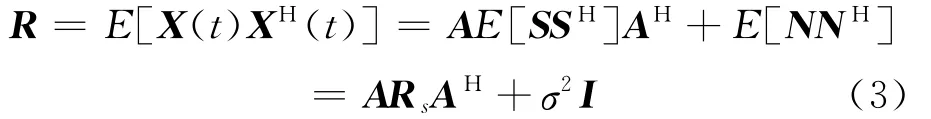
根据子空间分解理论，如果阵列数据的信号分量位于协方差矩阵R的一个低秩的空间，那么可以通过特征结构类的子空间方法将数据协方差矩阵分解为信号子空间和噪声子空间．

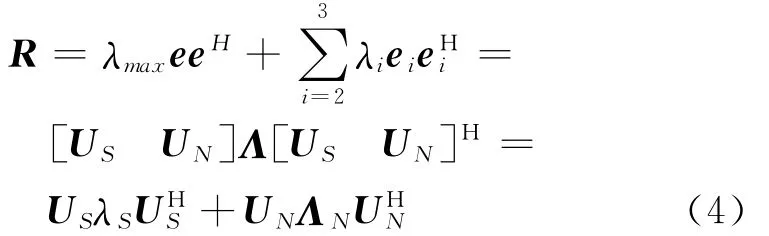
式中：ei是R的特征值λi对应的特征向量；Λ是由特征值组成的对角阵；λS为最大的一个特征值；ΛN为2个较小特征值组成的对角阵，大特征值对应的特征向量构成了信号子空间US，小特征值对应的特征向量构成了噪声子空间UN．

理想条件下数据空间中的信号子空间与噪声子空间是正交的，此时构造入射信号的导向矢量：

显然，若导向矢量a（θ）指向信号子空间时，其必与噪声子空间UN正交，则单矢量水听器MUSIC算法的空间谱估计表达式

考虑到实际接收数据矩阵是有限长的，即数据协方差矩阵R的最大似然估计为︵R＝XXH／N，并且由于噪声的存在，a（θ）与UN不能完全正交，因此需要进行空间谱搜索．

2 单矢量水听器USTC－MUSIC算法

由文献［3］定义单矢量水听器阵列矩阵X（t）的空时相关矩阵为

式中：0＜τ＜τmax根据式（3），有如下性质．

式中：τ≠0；Rs（τ）＝E［s（t－τ）sH（t）］，是信号的空时相关矩阵，对导向矩阵A（θ）作奇异值分解，A（θ）＝［EsEn］［D 0］TVH，代人式（8），可以看出对所有τ≠0，有

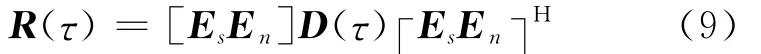
式中：D（τ）＝［DVHS（τ）VD 0］是一个块对角矩阵．Es，En分别是信号子空间和噪声子空间．传统子空间的分解方法是对R（0）进行的，而利用R（τ）进行奇异值分解获得信号子空间和噪声子空间，可以改进DDA估计的性能．

从上面的分析可见，对任何一个R（τ）进行奇异值分解都可以得到信号子空间和噪声子空间，为了克服不确定性可能导致R（τ）奇异的问题，定义：

在实际应用中，x（t）是由N 个快拍构成．因此，R（τ）和R分别由时间平均来代替，此时：

考虑酉矩阵：

式中：In为n×n阶矩阵；Jn为n×n阶交换矩阵；J2n＝Q2n，对R（τ）作酉变换并取实部构造的实数空时相关矩阵为［8］

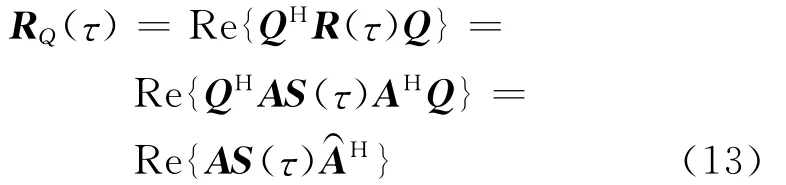
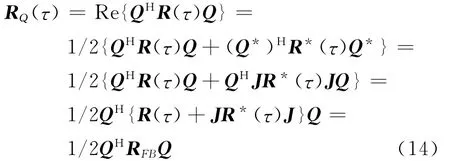
式中：RFB＝1／2［R（τ）＋JR＊（τ）J］，它是修正空间平滑子阵个数与阵元数相同时的情况．因此当噪声或信号源相干时，利用RQ进行奇异值分解的USTC－MUSIC算法可以分辨出相干信号．

3 仿真验证

考虑单个二维矢量水听器，分别仿真空时相关酉变换MUSIC算法与协方差矩阵MUSIC算法在非相干噪声、相干噪声背景下对双目标方位估计的对比结果，验证改进算法的性能优于原算法［6－8］．

3．1 非相干噪声背景下双目标方位估计

1）仿真条件 噪声为不相干的零均值高斯白噪声，入射目标方位角为θ1＝40°，θ2＝50°，频率f1＝25Hz，f2＝10Hz的2个不相关的单频目标，采样频率fs＝200Hz，样本点数N＝1 000，搜索步长为Δθ＝0．01°，改变信噪比，计算结果见图1．

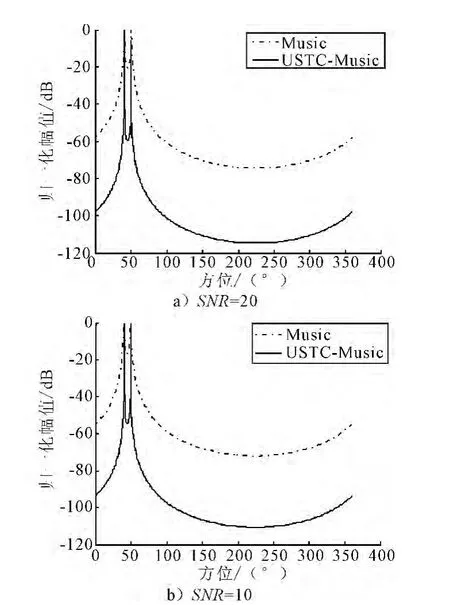
图1 不同信噪比目标方位估计

从图1可以看出，非相干噪声场中，两种算法都能准确估计两个目标的方位，并且新算法的方位估计波束旁瓣和束宽要明显小于原算法．

2）固定信噪比SNR＝20，估计2目标方位角分别为40°，45°和40°，43°情况下，计算结果见图2．

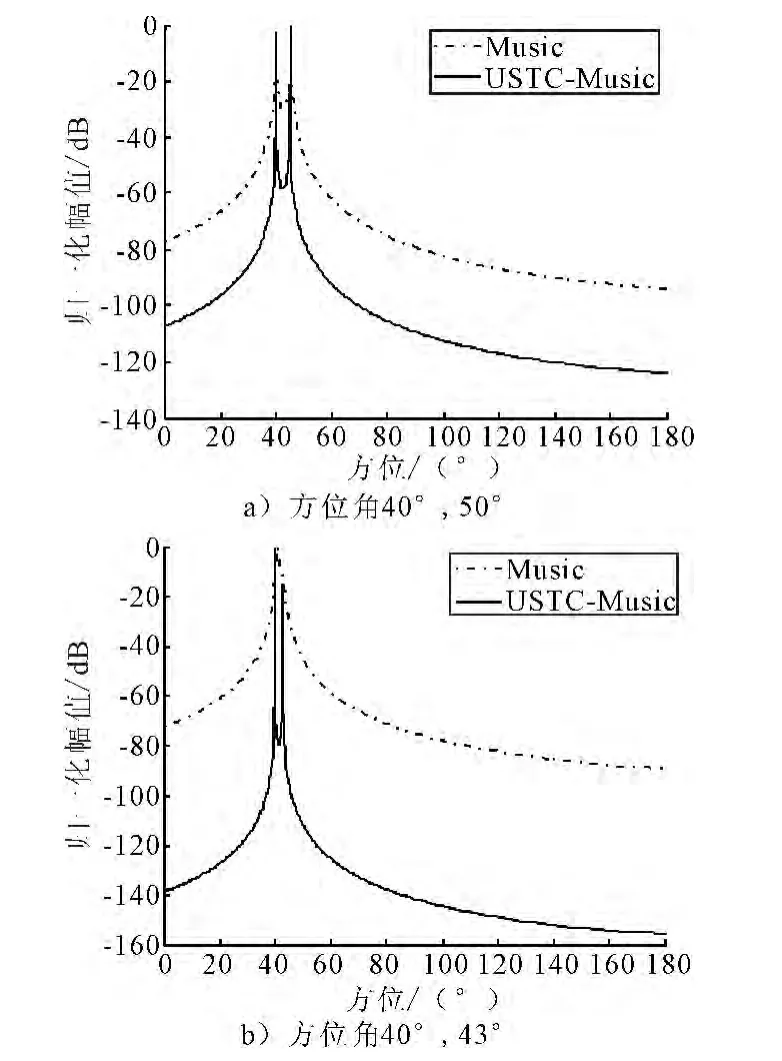
图2 非相干噪声背景下目标分辨力

由图2可知，原算法在目标方位相差5°时性能明显下降，方位相差3°时已不能分辨出两个目标，而新算法在相差3°时仍能较好的估计两个目标的准确方位．

3）非相干噪声场中非相干目标方位角分别为40°，43°，在不同信噪比下进行100次蒙特卡洛仿真，比较两种算法的分辨概率和均方根误差，见图3．

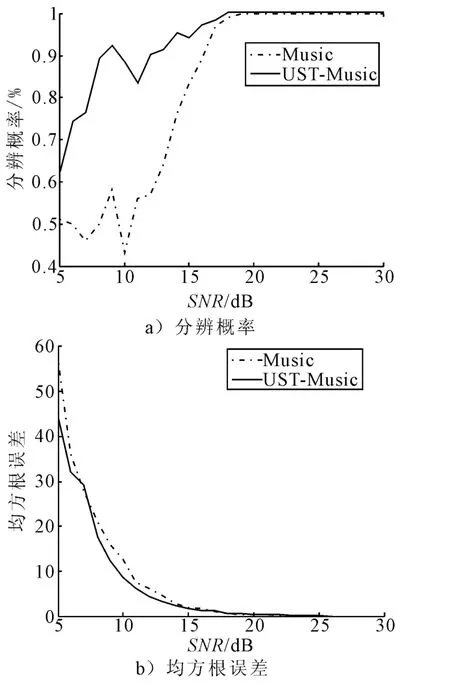
图3 算法性能分析

因此，由图3分析可得，新算法在非相干噪声场中对不相关的两目标进行方位估计时的分辨性能更好，均方误差相近．

3．2 相干噪声背景下双目标方位估计

1）仿真条件 噪声为相干噪声，频率f1＝25Hz，f2＝10Hz的2个不相关的单频目标信号，采样频率fs＝200Hz，样本点数N＝1 000，搜索步长为Δθ＝0．01°，信噪比SNR＝20，目标方位角分别为40°，45°和40°，43°情况下，计算结果见图4．

图4表明，原算法在相干噪声场中对2目标方位相差5°，3°时不能分辨出两个不相关的目标，而新算法仍能估计出目标的准确方位．

2）频率f＝25Hz、相位差30°的2个相干信号和信号幅度相差5倍的两强弱信号，目标方位分别为40°，50°情况下计算结果见图5．

由图5a）发现，原算法在相干噪声场中对两个方位角度相差较大（10°）的相干目标方位估计时会在2个角度中间产生一个虚假的方位估计最大值，在图5b）中原算法仅能估计出较强的目标方位，弱信号被掩盖．而新算法在上图两种情况下都能对两个目标方位进行估计．

图4 相干噪声背景下目标分辨力

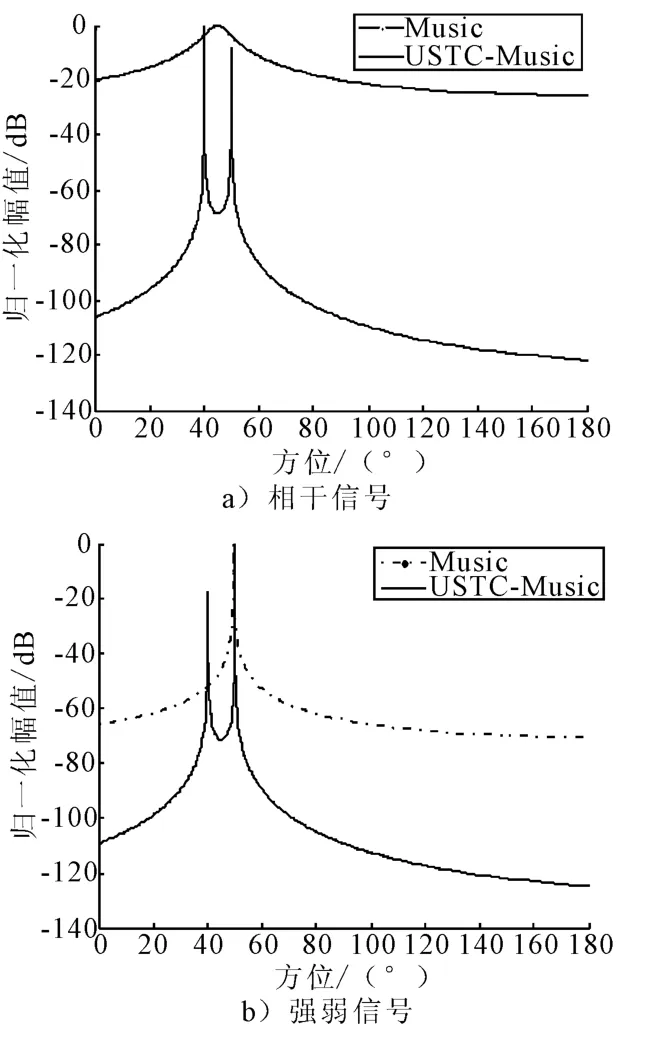
图5 相干噪声背景下相干目标分辨力

3）相干噪声场中非相干目标方位角分别为40°，43°，在不同信噪比下进行100次蒙特卡洛仿真，比较两种算法的分辨概率和均方根误差，见图6．

由图6可得，新算法在相干噪声场中对不相关的两目标进行方位估计的分辨性能比原算法更好，均方根误差更小．

图6 算法性能分析

4）相干噪声场中相干目标方位角分别为40°，43°，以及信号幅度相差5倍的两强弱信号，分别在不同信噪比下进行100次蒙特卡洛仿真，比较两种算法的分辨概率，见图7．

图7 算法分辨概率比较

由图7可得，新算法在相干噪声场和强弱信号时分别在10dB和14dB时能分辨两目标，而原算法则失效．

4 结束语

本文主要为了解决MUSIC算法在相干目标及相干噪声背景时难以准确估计目标方位的问题，提出利用阵列信号处理的空时相关矩阵酉变换MUSIC算法处理单矢量水听器同步测量的声压、振速信号．由不同信噪比非相干噪声和相干噪声背景下对非相关目标和相干目标方位估计的仿真分析可得，运用本文提出的单矢量水听器改进MUSIC算法不论噪声相关性的强弱，其噪声抑制能力和目标分辨能力均优于原方法．

［1］SHCHUROV V A．Coherent and diffusive fields of underwater acoustic ambient noise ［J］．Acoustic．Soc．Am，1991，90（2）：991－1001．

［2］姚直象，惠俊英，惠 娟，等．基于自适应算法的单矢量传感器抗相干干扰［J］．武汉理工大学学报：交通科学与工程版，2008，32（1）：138－141．

［3］惠俊英，李春旭，梁国龙，等．声压和振速联合信号处理抗相干干扰［J］．声学学报，2000，25（5）：389－394．

［4］孙岩松，李 平，李风华．海面噪声场条件下声压与振速的空间互相关函数［J］．海洋技术，2006，25（3）：13－16．

［5］何 劲，陈建文，刘 中．利用空时相关矩阵酉变换估计波达方向［J］．系统工程与电子技术，2005，25（5）：39－43．

［6］梁国龙，张 锴，付 进．单矢量水听器的高分辨方位估计应用研究［J］．兵工学报，2011，32（8）：986－990．

［7］HAARDT M，NOSSEK J A．Unitary ESPRIT：how to obtain increased estimation accuracy with a reduced computational burden［J］．IEEE Trans．On SP，1995，43（5）：1232－1242．

［8］孙贵青．矢量水听器检测技术研究［D］．哈尔滨：哈尔滨工程大学，2001．