城市快速路交通拥堵持续时间分布特性研究＊

张 轮 施奕骋 杨文臣 杨 涛

（同济大学道路与交通工程教育部重点实验室1） 上海 201804）（上海市交通信息中心2） 上海 200032）

0 引 言

国内外众多学者对城市交通拥堵形成机理和消散机理展开研究．何树林［1－2］、宋博等［3］认为造成我国城市道路交通拥堵的诱发原因是交通流运行状态的失稳，最根本原因是交通需求与供给的失衡，其本质是人与物的位移需求不断增长的状况与空间资源稀缺的矛盾．这类宏观研究从社会经济的角度解析交通拥堵形成原因，没有考虑城市交通流运行的动态特性，对交通拥堵传播特性和干预机制缺少研究．Chowdhury［4］、高自有等［5］从统计物理的角度将交通系统中的元素定义为交互的“粒子”，从动态网络交通流理论出发，分析突发事件所导致交通拥堵传播规律．这类微观研究选取排队长度等外在的状态参数表征交通拥堵的性能，采用阈值划定或模式特征识别等方法解析拥堵的开始、持续和结束，从较大粒度挖掘拥堵的形成原因和传播特性，对拥堵持续时间等交通拥堵关联的内在因素缺乏定量解析．

生存分析（survival analysis）对删失数据具有良好的处理能力，并可定量解释变量的时间变化特性，符合城市交通数据的时间序列和空间分布解析的内在要求［6］．近年来，生存分析及其非参数估计在交通领域的应用研究逐渐得到重视．Tiwari等采用生存分析研究了行人过街的等待时间［7］、航班延误时间［8］、道路铺面材料的疲劳失效时间［9］、高速公路交通事故的影响持续时间［10］和行人出行行为活动持续时间［11］，Chang等［12］利用生存分析中的Cox回归模型研究了影响机车使用寿命和排放的影响因素．周映雪等［13］首次将生存分析应用于分析北京市交通拥堵持续时间的时空分布规律，但缺少交通拥堵持续时间等影响因子的定量分析研究．

针对众多研究仅从排队长度等间接的外在特征参数解析交通拥堵发生、形成和和传播规律，交通拥堵的知识不仅受限于估计参数的精度和准度，且极少关注交通拥堵持续时间等直接的内在特征参数，本文以交通拥堵持续时间为研究对象，将生存分析引入交通拥堵时空分布特性的分析领域，提出一种城市交通拥堵时空分布特性的建模与分析方法，其依托上海市南北高架西侧的交通流检测数据，提出交通拥堵持续时间的生存分析流程，建立基于风险的拥堵持续时间模型，并采用非参数估计方法对其进行估计，在五类影响因素下，具体分析南北高架交通拥堵持续时间的时空分布规律．

1 交通拥堵持续时间的生存分析建模

1．1 交通拥堵生存分析的四个要素

交通拥堵生存分析的4个要素定义如下．

1）交通拥堵的生存时间 生存时间可以广泛地定义为某给定事件的发生时间．定义交通流处于拥堵状态即为事件发生，则道路上从拥堵发生到拥堵消散的持续时间，即交通拥堵持续时间（traffic congestion duration time，TCDT）为拥堵的生存时间．

2）交通拥堵的删截数据 相对于完全数据，删截数据是指某事件发生的时间段大于研究的时间段，即某事件发生的时间比研究开始的时间早或者该事件结束的时间比研究结束的时间晚，或者该事件在研究期间由于某些原因退出，使研究者不知道事件结束的具体时间，对于这类不完全数据称之为删截数据．据此，交通拥堵数据具有典型的删截特征．

3）交通拥堵的生存函数 表征交通拥堵事件发生至时间t（即在时刻t之后拥堵结束）的概率分布，用以描述拥堵持续时间的统计特征．记S（t）为生存函数，其定义为

式中：T为拥堵时间；F（x）为分布函数，当X为连续型随机变量时，生存函数与分布函数互补．根据定义，函数S（t）又称为累积生存概率，它的图形叫生存曲线．陡峭的生存曲线表示低的生存概率，较平坦的曲线表示高的生存概率．

4）危险率函数 是刻画生存时间的重要特征．危险函数实质上是条件生存率，表征交通拥堵事件在某时刻发生的条件下，在以后的单位时间Δt内结束的条件概率，危险率函数h（t）可定义为

式中：f（t）为T在时点t上的概率密度．

式中对危险率函数进行积分得到累积危险函数曲线，累积危险函数的位置越高，表征在下一单位时刻内，事件结束的概率越高，即表示下一时刻交通拥堵消散的概率越高．

1．2 Kaplan－Meyer非参数回归模型

Kaplan－Meyer（K－M）模型是一种非参数模型，在运用该模型时无需对其理论分布作出任何假设，应用K－M模型可直接估计交通拥堵持续时间的生存函数和危险函数，从而定量分析某一影响因子下的交通拥堵持续时间分布特性，同时，采用Log－rank时序秩检验可以分析影响因子对交通拥堵影响显著性假设的有效性．一般认为，当显著性检验特征值低于阀值0．05时，显著性假设成立．记T1＜T2＜…＜Tn代表n个拥堵时间的样本，则基于K－M模型的拥堵持持续时间生存函数S（t）的估计函数＾S（t）为

式中：Ti为完全样本，它表示T1至Tn中满足以下两个条件的样本：条件一，该样本为小于t的正整数；条件二，该样本为无删截数据．因而，当所有观察都无删截时，拥堵样本编号i的取值是连续的整数数列，否则i的取值不连续．

1．3 分析流程

面向城市道路交通拥堵管理的生存分析数据处理流程见图1．

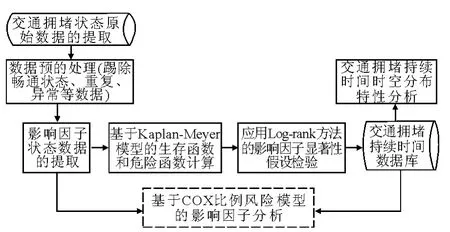
图1 面向交通拥堵管理的生存分析数据处理流程

2 实证分析

2．1 数据描述

研究的数据来源于上海市道路交通实时信息检测系统．选取上海市南北高架西侧的共计21个匝道断面为实证分析的案例（见图3），该路段由北向南贯穿上海城市中心，并连接上海内、中、外三环快速路，具有多处典型快速路拥堵路段黑点，如共和新路高架段、成都北路高架段等．基础数据记录取自的时间段为2012年11月1日至2012年11月20日，以及2013年3月1日至2013年3月20日，共计40d，120万条断面交通拥堵状态数据．基础原始数据的结构见表1，包括线圈编号，检测时间，每分钟的占有率、流量、平均车速以及路段状态等．其中，检测状态中的“21”“22”“23”分别代表“绿”（顺畅）“黄”（缓行）“红”（拥堵）3种路段交通状态．

图2 上海市快速路拥堵状态

图3 南北高架监测点布置

表1 交通拥堵的原始数据表

研究以红色堵塞状态表征路段交通拥堵事件，将红色状态的持续时间作为拥堵的生存时间，经过数据预处理共计得到了2 340条交通拥堵持续时间样本，并对每个样本记录按检测位置、星期数、高峰时段、数据年限和气候条件五类时空影响因素进行标志划分，提取到的数据样本的数据结构见表2．表2中，星期数，检测编号“1～21”表征21个交通数据采集的断面；检测位置编号“1”“2”“3”分别代表“内环内”“内环至中环”“中环至外环”；气候条件编号“0”“1”分别代表“非雨天”“雨天”；高峰时段编号“0”“1”“2”代表“其他时段”“早高峰”和“晚高峰”；数据年限编号“0”“1”代表“2012年”和“2013年”；“持续时间”的单位为分钟；删截状态编号“0”“1”分别代表 “删截数据”、“完整数据”．

2．2 交通拥堵持续时间的总体分布特性

遵循数据分析的流程，采用SPSS18．0实现交通拥堵持续时间生存特性的建模与分析．分析显示：南北高架最短的拥堵持续时间为1min；最长的拥堵持续时间为383min，平均拥堵持续时间为56min；平均每个断面每天发生交通拥堵2．8次，若除去午夜时段（从早6点至晚9点，1d15h计算），交通拥堵的平均时间占1d时间的17．3%．

南北高架拥堵持续时间的生存函数和风险函数随时间变化的规律见图4～5：约50%的交通拥堵在30min内消散，30%的交通拥堵在1h内消散，而拥堵持续时间超过2h的恶性拥堵的发生概率小于0．2，且交通拥堵持续时间在0～2h范围内的风险率均小于0．05，这表明在2h的时间段内，南北高架交通拥堵持续时间的分布比较均匀，并没有集中分布在某些数值附近，不具备显著的特征．

表2 交通拥堵持续时间的数据库表结构

图4 南北高架拥堵持续时间的总体生存函数

2．3 交通拥堵持续时间的时间分布特性

1）不同星期数的拥堵持续时间分布特性根据星期数，将交通拥堵持续时间样本划分为周一至周日7类．不同星期数的拥堵持续时间的生存函数和累积风险函数分别如图6～7．

图5 南北高架拥堵持续时间的总体风险函数

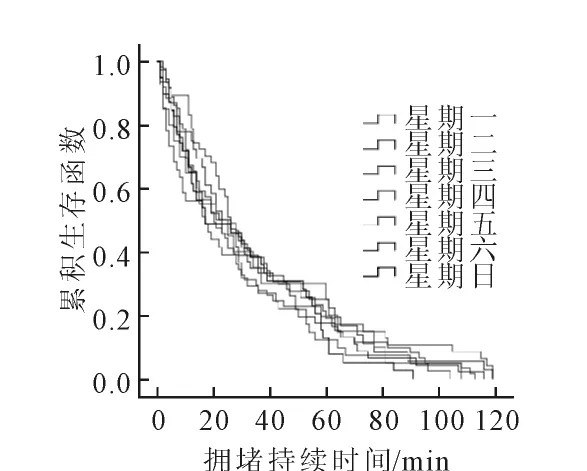
图6 不同星期数拥堵持续时间的生存函数

图7 不同星期数拥堵持续时间的累积危险函数

对工作日和非工作日，两者交通拥堵持续时间的分布规律一致，星期六和星期日并没有因为是非工作日而具有较小的拥堵持续时间，反而，20～60min的交通拥堵发生的概率高于星期四和星期五2个工作日．根据累积危险函数，周末不容易产生超过1h的长时间拥堵，拥堵更容易消散；而相比其他工作日和非工作日，周一的拥堵持续时间明显更长，产生超过1h的长时间拥堵的概率高，即周一的拥堵一旦开始形成，拥堵将难以快速消散，这与南北高架周一早高峰的拥堵现状相符．

2）不同高峰时段的拥堵持续时间分布特性根据交通拥堵的发生时段，将拥堵持续时间样本划分为早高峰（7点至10点）、晚高峰（16点至19点）和其他时段3类．采用Log－rank时序秩检验计算3个时段下拥堵持续时间的分布差异，得到的检验特征值均小于0．044，因而，不同时间段发生的交通拥堵的持续时间具有显著差别．图8～9给出了3个时段拥堵持续时间的生存函数和累积风险函数随时间的变化规律：在早高峰时段产生的交通拥堵的持续时间相对会更长，且更容易产生超过1h的长时间拥堵，而在晚高峰时段产生的交通拥堵基本可以在1h内消散．值得注意，在非高峰时段（即中午和晚上），南北高架发生的交通拥堵占到总体样本的42%，这说明南北高架交通拥堵的发生时段已不再是传统上早晚两个高峰，已呈现出波峰多、波长大的特点．

图8 不同高峰时段的拥堵持续时间的生存函数

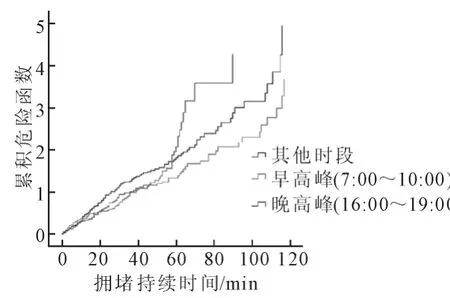
图9 不同高峰时段的拥堵持续时间的累积危险函数

3）不同数据年限的拥堵持续时间分布特性根据基础数据采集的2个时间段，将拥堵持续时间样本划分为2012年和2013年2类．采用Logrank时序秩检验计算2个年份的拥堵持续时间的分布差异，得到的检验特征值为0．01，可见2个年份的拥堵持续时间的分布具有显著差异．2个年份的拥堵持续时间的生存函数和累积风险函数分别见图10～11：2013年的生存函数和累积风险函数的曲线明显位于2012年相应曲线的上方，这表明2013年南北高架交通拥堵的消散速度在变慢，发生长时间拥堵的概率显著增加．这是因为2013年一季度上海私人小汽车的注册量同比增幅达12%，南北高架作为贯穿上海南北的交通大动脉，随着出行需求增加，拥堵状况愈发严重．

图10 不同数据年限的拥堵持续时间的生存函数

图11 不同数据年限的拥堵持续时间的危险函数

2．4 交通拥堵持续时间的空间分布特性

1）不同检测位置的拥堵持续时间分布特性根据交通拥堵发生的路段位置，将拥堵持续时间样本划分为内环内、内环至中环、中环至外环3类．采用Log－rank时序秩检验计算不同位置的拥堵持续时间的分布差异，得到的检验特征值均远小于0．05，这表明拥堵持续时间在不同的路段上的分布存在显著差异．图12～13给出了3个位置拥堵持续时间的生存函数和累积风险函数随时间的变化规律：内环的交通运行状况最好，平均18min内拥堵即可消散，拥堵持续时间最长也不超过1h；而中环至外环的拥堵状况最为严重，平均拥堵持续时间超过80min，发生超过2h的恶性拥堵的概率也相对较高．这主要是因为南北高架道路的不同路段的车道数存在差异．同时，内环至中环的路段存在多处设置不合理的匝道．

图12 不同检测位置的拥堵持续时间的生存函数

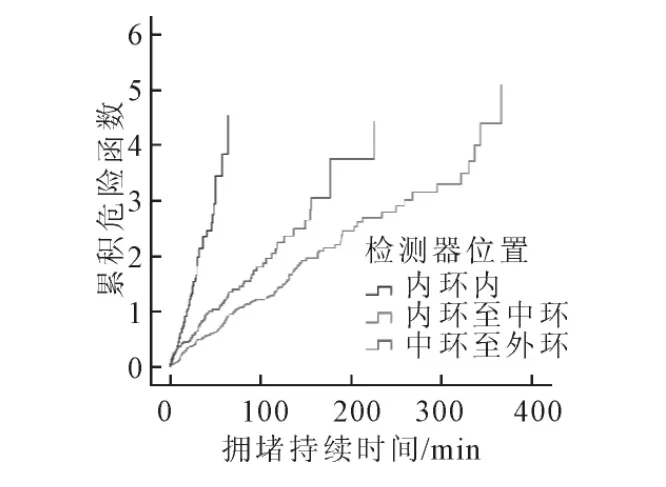
图13 不同检测位置的拥堵持续时间的累积风险函数

2）不同天气条件的拥堵持续时间分布特性根据交通拥堵发生时间的当时天气条件，将拥堵持续时间样本划分为雨天和非雨天两类．不同天气条件下拥堵持续时间的生存函数和累积风险函数分别见图14～15：在不同气候条件下，在1 h以内的交通拥堵的分布无明显差异；但气候条件对长时间交通拥堵的分布存在显著性的影响，雨天交通拥堵的消散速度慢，更容易产生长时间的拥堵．这是因为恶劣天气条件使驾驶的能见度降低，且天雨路滑导致车辆制动能力下降，高架路上行驶的车辆被迫降低行车速度，车流运行缓慢．

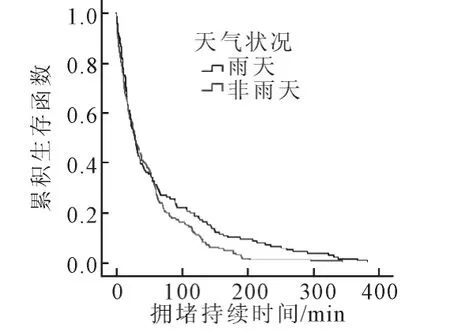
图14 不同天气条件的拥堵持续时间的生存函数

图15 不同天气条件的拥堵持续时间的累积危险函数

3 结 论

1）从整体上看，南北高架道路拥堵的平均持续时间约1h，近50%的交通拥堵在0．5h内消散，约有20%的交通拥堵的持续时间会超过100 min．

2）拥堵持续时间的分布具有一定的时间特性．工作日和非工作日的交通拥堵状况同样严重，相比其他星期数，周一更容易发生拥堵；对于不同的高峰时段，早高峰更容易产生长时间的拥堵，而城市快速路在非高峰时段的拥堵业已呈现出波峰多、波长大的特征；受上海机动车化的影响，2013年南北高架的拥堵状况相比2012年在恶化．

3）拥堵持续时间的分布具有一定的空间特性．在不同的检测位置，内环至中环路段的拥堵持续时间大幅超过中环至外环及内环内路段的拥堵持续时间，拥堵消散的时间更长；对于不同的气候条件，雨天更容易产生长时间的拥堵．

［1］曹 静，宫 建，杨孝宽．解决北京市潮汐性交通拥堵的措施研究［J］．武汉理工大学学报：交通科学与工程版，2009，33（6）：1116－1119．

［2］何树林．运用供需平衡理论解析城市道路交通拥堵机理［J］．中国人民公安大学学报：自然科学版，2012，18（2）：48－52．

［3］宋 博，赵 民．论城市规模与交通拥堵的关联性及其政策意义［J］．城市规划，2011，6（5）：55－58．

［4］CHOWDHURY D，SANTEN L，SCHADSCHNEIDER A．Statistical physics of vehicular traffic and some related systems［J］．Physics Reports，2000，329（4）：199－329．

［5］高自友，龙建成，李新刚．城市交通拥堵传播规律与消散控制策略研究［J］．上海理工大学学报，2011，33（6）：701－708．

［6］ WASHINGTON S P，KARLAFTIS M G，MANNERING F L．Statistical and econometric methods for transportation data analysis［M］．Chapman ＆Hall，CRC，2009．

［7］TIWARI G，BANGDIWALA S，SARASWA A，et al．Survival analysis：pedestrian risk exposure at signalized intersections［J］．Transportation Research Part F：Traffic Psychology and Behaviour，2007，10（2）：77－89．

［8］WONG J T，TSAI S C．A survival model for flight delay propagation［J］．Journal of Air Transport Management，2012，23：5－11．

［9］WANG Y H，MAHBOUB K C，HANCHER D E．Survival analysis of fatigue cracking for flexible pavements based on long－term pavement performance data［J］．Journal of Transportation Engineering，2005（8）：608－616．

［10］NAM D，MANNERING F．An exploratory hazardbased analysis of highway incident duration［J］Transportation Research Part A：Policy and Practice，2000，34（2）：85－102．

［11］KHAROUFEH J P，GOULIAS K G．Nonparametric identification of daily activity durations using kernel density estimators［J］．Transportation Research Part B：Methodological，2002，36（1）：59－82．

［12］CHANG H L，YEH T H．Regional motorcycle age and emissions inspection performance：a Cox regression analysis［J］．Transportation Research Part D：Transport and Environment，2006，11（5）：324－332．

［13］周映雪，杨小宝，环 梅，等．基于生存分析的城市道路交通拥堵持续时间研究［J］．应用数学和力学，2013，34（1）：98－106．