基于双框架变速控制力矩陀螺的航天器姿态控制研究
2014-01-17袁建平
陈 璐,袁建平
(西北工业大学 航天飞行动力学技术重点实验室,陕西 西安 710072)
随着空间技术的快速发展,许多空间任务对航天器的姿态机动能力有更高的要求,快速、稳定、高精度的姿态控制系统成为空间技术的重要研究方向。
目前用于卫星姿态机动主动控制的执行机构类型主要有推力器、反作用飞轮、控制力矩陀螺等。控制力矩陀螺包括单框架控制力矩陀螺 (SGCMG)和双框架控制力矩陀螺(DGCMG)。如果转子转速可变,两者又可变为变速控制力矩陀螺(VSCMG)和双框架变速控制力矩陀螺(DGV)。控制力矩陀螺的工作原理是,高速转子(以下也称飞轮)自转轴方向绕框架轴转动,引起飞轮自转角动量进动而输出力矩。相比RW,CMG的输出力矩则大得多,且响应速度更快,功耗更低且使用寿命长。控制力矩陀螺的这些优点,使其成为最有前景的航天器姿态执行机构,并在国内外的许多航天器系统中(如 “ISS”和天宫一号等)得到应用[1-2]。
VSCMG比CMG多一个自由度,因此可以避免CMG群的奇异性。VSCMG是Ford和Hall等人[3]在1997年的AAS/AIAA的飞行力学专业会议上以“框架动量轮”的形式首次提出的。Schaub等人[4]将其命名为VSCMG,并推导基于单CMG和多CMG航天器的动力学方程,并设计了基于速度、加速度的操纵律实现航天器的姿态控制。Yoon研究了基于一个VSCMG的航天器角速度和姿态控制问题[5],研究了VSCMG群的奇异特性,提出了避免奇异的零运动方法,研究了基于VSCMG航天器的能量/姿态一体化控制系统的自适应控制律。
从上世纪60年代开始,基于DGCMG的航天器姿态控制成为研究的热点。Bauer[6]采用四杆连接的分析方法研究了基于DGCMG航天器的运动学和动力学方程。Ahmed[7]利用Lagrange方程建立了DGCMG的动力学模型,研究了一种自适应反馈控制律来实现姿态跟踪。Liu等人[8]提出了一种采用转子可变速DGCMG为执行机构的空间飞行器姿态最优控制律,采用连续逼近方法,通过变分法估计性能指标变化,应用最速下降法和共轭梯度法得到期望解。周荻[9]研究了基于DGCMG群的航天器姿态动力学模型,设计了稳定的非线性控制律和奇异鲁棒+零运动操纵律,并进行了不同构型DGCMGs系统的奇异性分析。
无论是VSCMG还是DGCMG,它们都只有两个自由度,无法实现三维的姿态控制,为此,文中研究了双框架变速控制力矩陀螺(DGV)。由于DGV有3个自由度,其能完成三维的航天器姿态机动。本文推导了基于DGV的航天器姿态动力学模型,然后用Lyapunov稳定性理论设计了该非线性系统的控制律和操纵律,并研究了基于加速度的操纵律,仿真结果表明,该执行机构能够很好地实现航天器三维的姿态跟踪和快速机动。
1 基于DGV的航天器姿态动力学模型
如图1所示,DGV主要由外框架、内框架、转子和力矩电机等一些其它附件组成。外框架轴与内框架轴互相垂直,内框架轴与转子轴互相垂直,转子转速可变,因此DGV系统具有3个转动自由度。
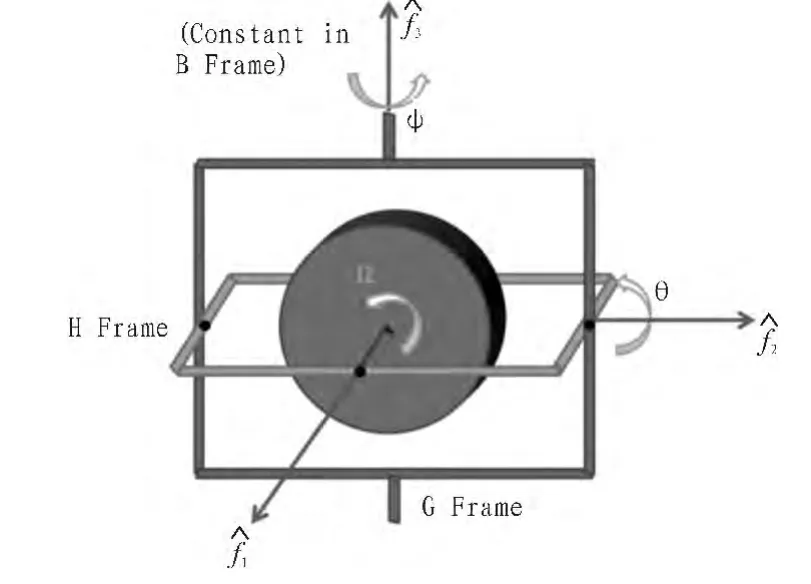
图1 DGV结构示意图Fig.1 The structure of a DGV
本文将航天器本体部分视作刚体,由于控制力矩陀螺框架连同转子相对于上述部分发生转动,所以以控制力矩陀螺系统作为执行机构的刚体航天器为多刚体系统。基于此,本文拟采用矢量力学建模方法。此外,本文研究中还做出如下假设:假设DGV的框架、转子质量均匀分布,安装也完全对称。因此,DGV的内外框架及转子质心重合,即为DGV的质心,由此得出基于DGV的航天器系统质心位置保持不变。
1.1 坐标系定义及转换关系
定义N-xNyNzN为惯性坐标系,简写为{N};定义C-xByBzB为航天器本体坐标系,质心为航天器质心C,简写为{B};定义O-xFyFzF、O-xGyGzG、O-xHyHzH分别为 DGV 的外框架、内框架和转子固连的坐标系,简写为 {F}、{G}、{H},三者质心均为DGV的质心O,单位向量分别为{f→1,f→2,f→3}、{g→1,g→2,g→3}、{h→1,h→2,h→3}。
矩阵[AB]表示坐标系 A 相对于 B 的方向余弦,[Mi(α)]表示绕某一固定轴旋转角度的旋转矩阵。外框架坐标系(F系)到内框架坐标系(G系),内框架坐标系(G系)到转子坐标系(H系)的欧拉角分别为ψ和θ,其旋转轴分别为f→3和g→2。本文中,左上标表示坐标系,右上标表示坐标原点。
坐标系之间的转换矩阵如下:
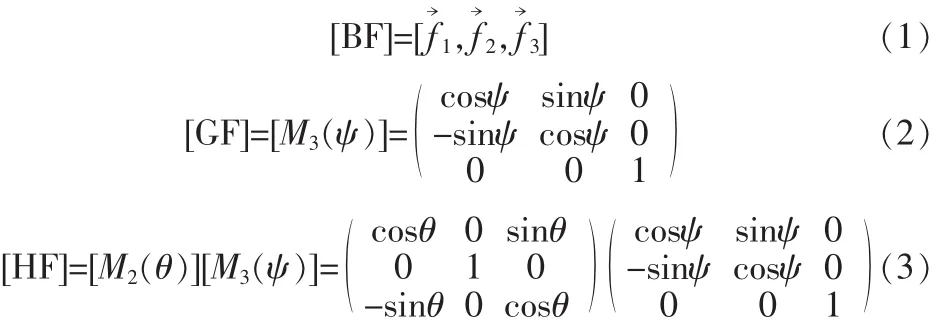
其中,[BF]表示DGV的安装矩阵,是固定的。
坐标系间的相对角速度可以用角速率与旋转轴的乘积表示:

1.2 航天器姿态运动学方程
由于四元数在描述刚体转动时有以下优点:不包含三角函数、运算简单、没有奇点等,所以文中采用四元数作为姿态描述参数,基于四元数的航天器姿态运动方程为:

1.3 基于DGV的航天器姿态动力学方程
航天器系统关于其质心C的角动量为:

将上式投影到本体系B下,并将转动惯量的导数代入,整理可得精确的基于DGV的航天器姿态动力学方程:

其中,[I]=B[I]=B[IS]+B[IG]+B[IG]+B[IH]+B[IW],T→ext表示航天器所受的外力矩,两者都是在本体系B下。
2 控制系统设计
从基于DGV的航天器系统动力学模型中我们可以看出,DGV的输出力矩是三维的,而其他附加项对航天器本体的作用也是在三维,所以,必须设计稳定的控制律,以实现航天器的三维姿态机动。本节的主要目标就是,根据Lyapunov稳定理论,设计一种稳定的控制律,能实现航天器跟踪期望的姿态轨迹。
2.1 控制律设计

本节控制律设计的目的就是,使本体坐标系B和参考系R之间的角速度、姿态趋于0。
构造Lyapunov函数:

对Lyapunov函数进行微分:

Lyapunov稳定性理论要求V˙必须是负半定,才能保证系统的稳定性。设P为一正定的角速度反馈增益矩阵,则V˙可表示为

结合两式,可得稳定性约束为:
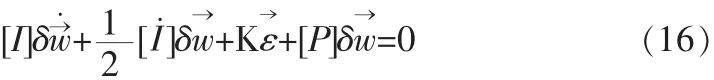
参考转移定理,可得如下关系

将基于DGV的航天器姿态动力学方程(9)代入式(18),整理可得如下的Lyapunov稳定性约束:


上式被称作“控制律”。
2.2 基于速度的操纵律设计
为了尽可能发挥“力矩放大效应”,操纵律方程(24)中框架转动角速度项要尽可能大,而惯性项(加速度项)应尽可能小,因此,忽略框架的加速度项ψ¨和θ¨,可得如下的操纵律方程:

上式与VSCMG的操纵律方程相似,但又包含二次项和。由于二次项的存在,VSCMG的相关操纵律解法并不适用。因此,本文采用牛顿法直接求解上述操纵律方程[17]。
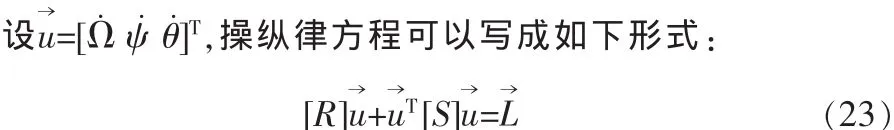
其中,[R]、[S]分别为[3×1]和[3×3]矩阵,但其中每一项都为[3×1]向量,具体如下:

上述操纵律方程不能解析求解,但可以用牛顿法求解如下方程组的根:

忽略二次项,可以得到如下的初值猜测:

采用下式进行循环迭代,直至误差|f(u→)|足够小:

在文中后面的仿真过程中,误差限取为10-9N·m。仿真结果表明,避免奇异的情况下,操纵律方程可以很快求得结果。
3 仿真及结果分析
文中基于Matlab仿真环境编制程序来验证所推导的航天器姿态动力学模型及非线性反馈控制律和操纵律。航天器各部分的转动惯量矩阵如下:
B[IS]=diag([15 45 30]) kg·m2G[IG]=diag([0.04 0.02 0.02]) kg·m2H[IH]=diag([0.02 0.02 0.04]) kg·m2H[IW]=diag([0.3 0.2 0.2]) kg·m2
航天器的姿态跟踪主要研究对于期望机动轨迹的跟踪问题,文中选取四元数为姿态描述参数,四元数以正弦规律变化,可以求得期望角速度也按正弦规律变化。参考轨迹姿态四元数的初值为q→(t0)=[0.5 0.5 0.5 0.5],角速度初值为w→(t0)=[-0.05 0.2 0]rad/s。转子的转速初值为 Ω(t0)=500 rad/s,内外框架角、框架角速率初值均为0。
仿真中采用本文所设计的非线性反馈控制律和基于加速度的操纵律,具体的仿真参数为K=200,[P]=diag([200 200 200]),Kψ˙=0.04,Kθ˙=0.2。 仿真时间设定为 60 s,仿真结果如图2~图5所示。

图2 航天器姿态(四元数描述)Fig.2 Attitude of spacecraft body(quaternion)

图3 航天器本体角速度Fig.3 Angular velocity of spacecraft body
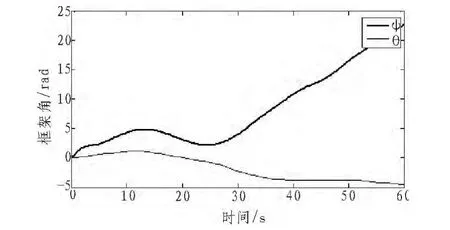
图4 框架角度Fig.4 Gimbal angles
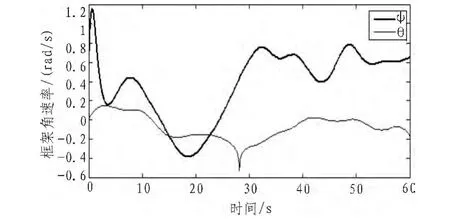
图5 框架角速率Fig.5 Gimbal rates
图2 、3可以看出,在仿真时间15 s左右,航天器的跟踪误差已经很小,达到10-4量级,由此可以说明基于加速度的操纵律,能很好地实现航天器的姿态跟踪。图4、5显示了在姿态跟踪过程中框架角和框架角速率的变化曲线,其中转子的角速度在500 rad/s附近。图5中,在28 s附近,内框架角速率有一处波动,这是由于此时内框架通过奇异位置(θ=-90°),和前文的奇异分析很好地吻合。
4 结 论
本文推导了精确的基于DGV航天器系统的数学模型,并基于Lyapunov稳定性理论设计稳定的反馈控制律和操纵律,实现跟踪参考轨迹。研究了更为精确的基于加速度的操纵律。仿真结果表明,一个DGV作为姿态执行机构即可完成航天器三维方向的姿态跟踪。
[1]Gurrisi C,Seidel R,Dickerson S,et al.Space station control moment gyroscope lessons learned[R].Proceedings of the 40th Aerospace Mechanisms Symposium,NASA NASA/CP-2010-216272, Kennedy Space Center,2010:12-14.
[2]张志方,董文强.控制力矩陀螺在天宫一号目标飞行器姿态控制上的应用[J].空间控制技术与应用,2011,37(6):52-59.ZHANG Zhi-fang,DONG Wen-qiang.The application of control moment gyro in attitude control of Tiangong-1 spacecraft[J].Aerospace Control and Application,2011,37(6):52-59.
[3]Ford K A,Hall C D.Flexible Spacecraft Reorientations Using Gimbaled Momentum Wheels[C]//Proceedings of the AAS/AIAA 1997 Astrodynamics Specialist Conference,edited by F.Hoots, B.Kaufman, P.Cafola, and D.Spencer, Univelt, Inc., San Diego, CA, 1997.
[4]Schaub H.Novel Coordinates for Nonlinear Multibody Motion with Applications to Spacecraft Dynamics and Control[D].Texas A&M University,1998.
[5]Yoon H.Spacecraft Attitude and Power Control Using Variable Speed Control Moment Gyros[D].Georgia Institute of Technology,2004.
[6]Bauer R J.Kinematics and dynamics of a double-gimbaled control moment gyroscope [J].Mechanism and Machine Theory,2002(37):1513-1529.
[7]Ahmed J,Bernstein D S.Adaptive Control of Double-Gimbal Control-Moment Gyro with Unbalanced Rotor[J].Journal of Guidance,Control and Dynamics,2002,25(1):105-115.
[8]Liu T C,Chubb W B,Seltzer SM,et al.Optimal control of a variable spin speed CMG system for space vehicles[C]//IEEE Conference on Decision and Control,incl Symp on Adapt Processes.San Diego:CA,USA ,1973:722-726.
[9]周荻,周净扬.基于双框架控制力矩陀螺的空间飞行器非线性姿态控制[J].宇航学报,2009,30(1):179-187.ZHOU Di,ZHOU Jing-yang.Nonlinear attitude control of spacecraft based on double gimbaled control moment gyroscopes[J].Journal of Astronautics,2009,30(1):179-187.
[10]Oh H S,Vadali SR.Feedback control and steering laws for spacecraft using single gimbal control moment gyros[J].Journal of the Astronautical Sciences,1991,39(2):183-203.
