某类p-叶负系数函数族的性质

李元林，费 华， 胡 琳

（江西理工大学，a.理学院;b.建筑与测绘工程学院，江西 赣州341000）

某类p-叶负系数函数族的性质

李元林a，费 华b， 胡 琳a

（江西理工大学，a.理学院;b.建筑与测绘工程学院，江西 赣州341000）

文中基于解析函数族常有的性质，令Sp（n）是在单位开圆盘上的解析函数族，并构建新的p－叶负系数解析函数族Tp（n，λ，α，β），且Tp(n，λ，α，β)是Sp(n)的子族.再利用Owa等人的研究结论和方法得到解析函数族Tp（n，λ，α，β）的系数估计、偏差定理、极值点、Hadamart乘积和积分算子等常有的解析性质．

负系数；解析函数；系数估计；偏差定理

0引言

解析函数是复分析研究中的一类重要的函数，国内外许多数学工作者很早就开始了这方面研究，并取得了极大的成效．在早期，单叶正系数解析函数的性质研究相对较多，并得到了系数估计、偏差定理、极值点、Hadamart乘积、积分算子等一些解析函数常有的性质，读者可参考文献[1,2]．文献[3]通过新定义的函数族，给出了单叶负系数解析函数族常有的性质．文献[4,5]研究了某类解析函数族的极值点，但对此函数族的偏差定理等其它解析性质还没进一步说明．文献[6,7]给出了某类解析函数的Hadamart乘积等性质，但忽略了该族函数的偏差定理和极值点等性质．近年来，又有了进一步的拓展，由单叶推广到p-叶（p为正整数）.文献[8-12]对p-叶解析函数的系数估计、偏差定理、极值点和Hadamart乘积等性质进行了研究，得到了负系数解析函数族常有的性质．而文献[13,14]通过构建新的函数族，得到了p-叶负系数解析函数族的领域，但并未考虑系数估计、偏差定理等其它的解析性质.因此，研究p-叶负系数解析函数的一些相关解析性质是具有重要意义的．

文中通过一个具体的p-叶负系数解析函数族Tp（n，λ，α，β），利用Owa等人的研究结论和方法得到解析函数族常有的解析性质，如系数估计、偏差定理、极值点、Hadamart乘积和积分算子等，从不同的侧面反映了函数族特有的性质，又进一步完善了p-叶负系数解析函数族的理论体系.

1 预备知识

TP（n，α）是由f（z）∈Sp（n）且满足α所作成的类，其中0≤α＜1.

定义1 复平面区域D上的解析函数f（z），若对D中任意的不同两点z1，z2，且z1≠z2，有f（z1）≠f（z2），就称作f（z）是单叶的解析函数.

定义2 设X是拓扑线性空间，U是X的一个非空子集，x0是U的一个元素，如果x0不能表示成U的两个不同元素的真线性凸组合，则称x0是U的一个极值点，记U极值点集为EU.

命题1[5,15]u∈EU的充要条件是若且 0＜t＜1，x,y∈u，且u=tx+（1-t）y，则x=y.

定义4 Ho¨lder′s inequality的表现形式：

下面定义一个新的负系数函数族：

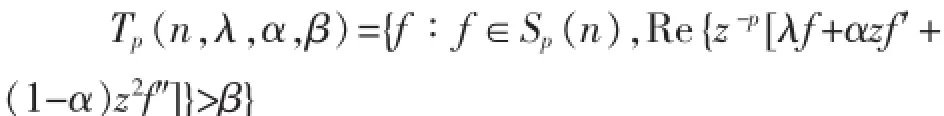
其中0≤α＜1，0≤β＜λ≤1.文中的目的就是要找出Tp（n，λ，α，β）的系数估计、偏差定理、极值点、Hadamart乘积和积分算子等一些解析性质.

2 主要结果

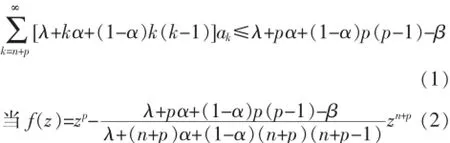
时，结论是严格的.

证 明：设f（z）∈Tp（n，λ，α，β），则Re{z-p[λf+ αzf′+（1-α）z2f″]}＞β，

即：Re{z-p[λf+αzf′+（1-α）z2f″]}＝Re{[λ+pα+

当z取实数且当α→1-时，则有：

反之，由于：

可得：

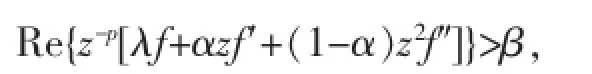
所以f（z）∈Tp（n，λ，α，β）.显然，当f（z）如式（2）时等号是成立的.

这就是Tp（n，λ，α，β）的系数估计.下面给出该定理的三个相关推论.

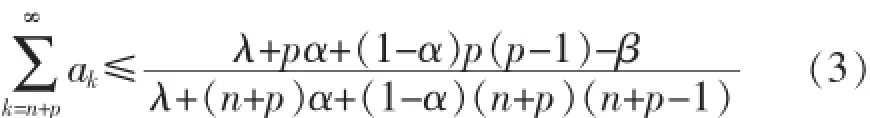
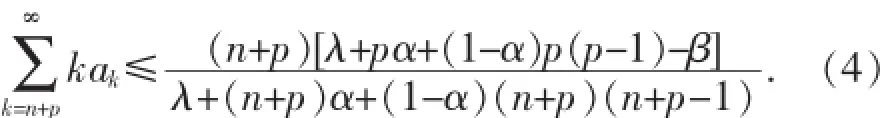
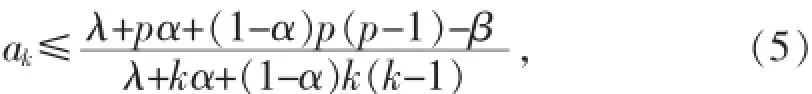
其中k=n+p，n+p+1，….

由此可以得到Tp（n，λ，α，β）的偏差定理，如下:

及

根据式（3）及式（4）容易得证．

定理3 令若 f（z），g（z）∈Tp（n，λ，α，β），则h（z）=（1-t）f（z）+tg（z）∈Tp（n，λ，α，β），其中0≤t≤1.

证 明：令

由g（z）∈Tp（n，λ，α，β），根据定理1，可得：

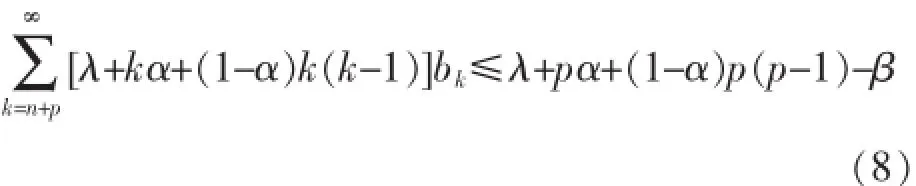
由式（1）及式（8），可得：

所以h（z）∈Tp（n，λ，α，β）．

下面来证函数族Tp（n，λ，α，β）的积分算子．

则：

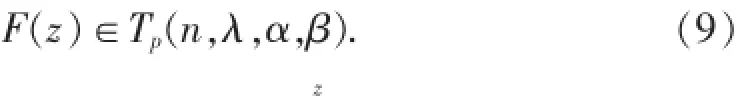
故定理得证．

定理5 令fn+p-1（z）=zp，若f（z）∈Tp（n，λ， α，β），则f（z）当且仅当可以展成的形式，其中

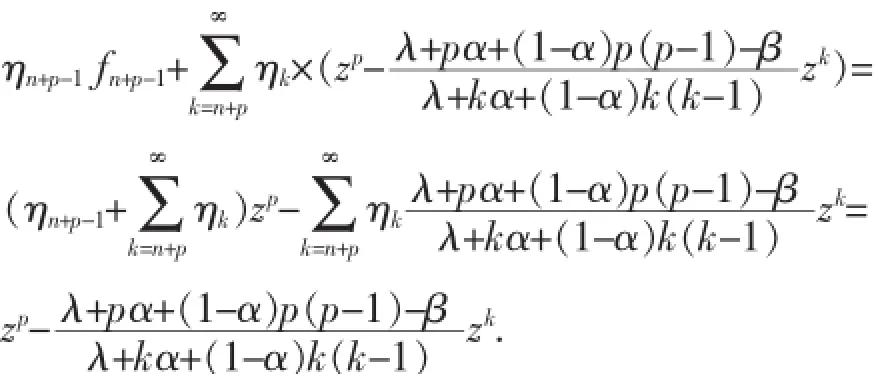
由于：

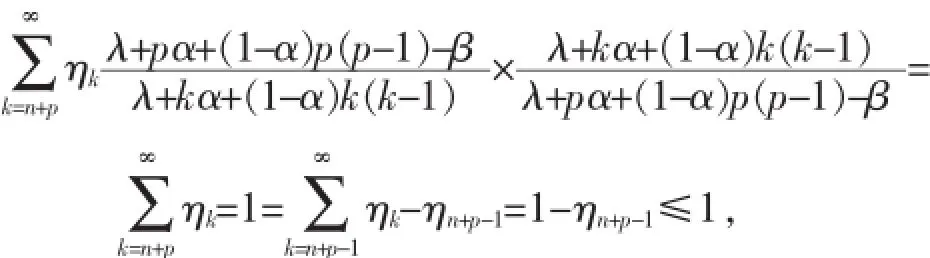
所以：

λ+pα+（1－α）p（p-1）－β．

由此可得f（z）∈Tp（n，λ，α，β）．

通常把定理3和定理5称为函数族Tp（n，λ，α，β）的线性关系.

由定理5，便可得到Tp（n，λ，α，β）的一个重要的性质：

推论4 Tp（n，λ，α，β）的极值点是：其中k=n+p，n+p+1，…

定理6 令f（z）∈Tp（n，λ，α，β），则f（z）将z＜1的圆盘映成一个包含的区域.

证 明：由式（6）右半部分及令r→1时可得到结论，证明略.

下面来证明Tp（n，λ，α，β）的Hadamart乘积性质.

定理7 若f（z），g（z）∈Tp（n，λ，α，β），则f*g∈Tp（n，λ，α，β），

其中γ＝λ+pα+（1－α）p（p-1）－

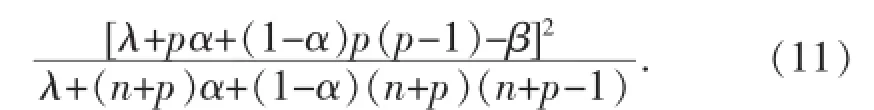
证 明：由式（1）及式（8），可得：

关键要找最大的γ，使得：

要使式（13）成立，假若：

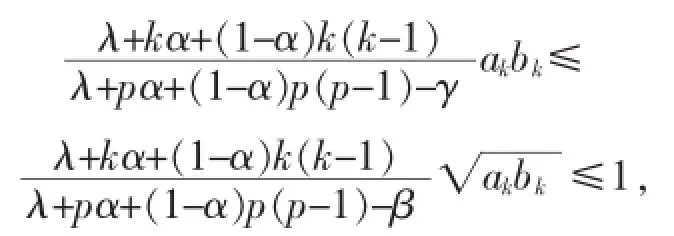
由式（12）可得：

令：

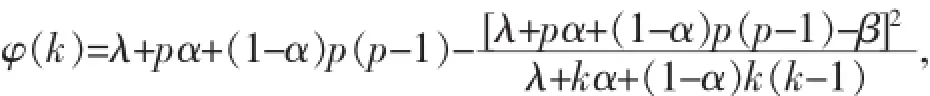
显然，φ（k）是关于k的单调递增函数，所以：

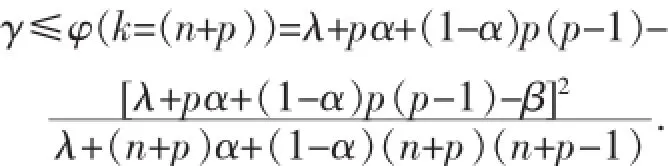
定理得证.

3结论

文中给出p-叶负系数解析函数族Tp（n，λ，α，β）的系数估计、偏差定理、极值点、Hadamart乘积和积分算子等常有的解析性质，内容上覆盖了解析函数类所涉及的常有的解析性质.而所研究的函数族对象的确立不仅兼顾了当前函数类研究的动向，而且保证了与早期同行研究的衔接，不仅对p-叶负系数解析函数的研究有一定的参考价值，而且对p-叶负系数解析函数族的理论体系有了进一步完善.

[1]Owa S,Nunokawa M,Saitoh H,et al.Close-to-convexity, starlikeness and convexity of certain analytic functions[J].Applied Mathematics Letters,2002,15(1):63-69.

[2]Altilntas O,Irmak H,Owa S,et al.Coefficients bounds for some families of starlike and convex functions of complex order[J]. Applied Mathematics Letters,2007,20(12):1218-1222.

[3]Darwish H E.On the coefficients of some subclasses of univalent functions[J].Southeast Asian Bulletin of Mathematics,2001,25(1): 75-86.

[4]Barmish B R,Kang H I.A survey of extreme point results for robustness of control systems[J].Automatica,1993,29(1):13-35.

[5]熊良鹏,刘晓丽.一类固定系数解析函数的极值点与支撑点[J].湖北大学学报,2012,34(2):215-217.

[6]Choi J H,Kim Y C,Owa S.Generalizations of Hadamard products of functions with negative coefficients Math [J].Journal of Mathematical Analysis and Applications,1996,199(2):495-501.

[7]Ruscheweyh St,Sheil-Small T.Hadamard products of Schlicht functions and the Pólya-Schoenberg conjecture[J]．Commentarii Mathematici Helvetici,1973,48(1):119-135.

[8]潘丽丽,刘 佳,熊良鹏．一类P-叶负系数解析函数[J]．湖北大学学报,2011,33(2):240-244．

[9]Orhan H,Kiziltunc H.A generalization on subfamily of p-valent functions with negative coefficient[J].Applied Mathematics and Computation,2004,155(2):521-530.

[10]Khalida I N.Some classes of p-valent functions defined by certain integral operator [J]. Applied Mathematics and Computation,2004,157(3):835-840.

[11]Orhan H.A ne w class of analytic functions with negative coefficients[J].Applied Mathematics and Computation,2003,138 (2／3):531-543.

[12]Orhan H,Kamali M.Fractional calculus and some properties of certain starlike functions with negative coefficients[J].Applied Mathematics and Computation,2003,136(2／3):269-279.

[13]桂贤敏，赖新兴．两类具有负系数的解析函数类的邻域[J]．江西理工大学学报,2009,30(2):35-36．

[14]Kamali M.Neighborhoods of a new class of p-valently starlike functions with negative coefficients[J].Mathematics Inequalities &Applications,2006,9(4):661-670.

[15]Rudin W.Functional analysis[M].Beijing:China Machine Press, 2004.

The properties of a certain analytic functions with negative coefficient

LI Yuan-lina，FEI Huab，HU Lina

(a.Faculty of Science;b.School of Architectural and Surveying&Mapping Engineering, Jiangxi University of Science and Technology,Ganzhou 341000,China)

In this paper,based on the generalizations of analytic functions,let Sp(n)be the class of functions which were univalent and analytic in the open unit diskA new subclass Tp（n，λ，α，β）of Sp(n)is introduced．According to the conclusions obtained by Owa et al.we obtain some properties in Tp（n，λ，α，β）, such as coefficient estimate,growth and distortion theorems,extreme point,Hadamart product,fractional calculus and so on.

negative coefficient;analytic functions;coefficient estimate;growth and distortion theorem

O174.51

A

2095-3041（2014）00-0094-04

10.13265/j.cnki.jxlgdxxb.2014.01.016

2013-06-26

国家自然科学基金资助项目（11326238）；江西省教育厅基金项目(GJJ13369)

李元林（1983- ），女，助教，主要从事复分析等方面的研究，E-mail:liyuanli20090606@163.com.