非马尔科夫环境下依赖于纯度的纠缠制备
2014-01-16李艳玲徐中辉
李艳玲,徐中辉,霍 良
(江西理工大学信息工程学院,江西 赣州341000)
非马尔科夫环境下依赖于纯度的纠缠制备
李艳玲,徐中辉,霍 良
(江西理工大学信息工程学院,江西 赣州341000)
考虑了两个无相互作用的量子比特系统和一个处于零温非马尔科夫库耦合的情况.研究发现,当系统初始处于两体可分离混合态时,非马尔科夫环境可以诱导两量子比特间的纠缠,其值的大小高度依赖于体系所处态的初始纯度.此外,非马尔科夫库诱导的纠缠远大于马尔科夫库诱导的纠缠,并且随着失谐量的增大,诱导纠缠的最大值会大幅度增加.研究表明,在非马尔科夫情况下,可以通过增大系统与非马尔科夫库之间的失谐量制备量子比特间的高度纠缠态,进而完成量子信息处理的任务.
非马尔科夫库;诱导纠缠;纯度
0引言
在量子信息和量子计算理论中,纠缠起着非常重要的作用,是量子信息和量子计算得以实现的基本资源[1].而实际的量子系统不可避免的会与周围环境作用,因此,研究开放系统的动力学是非常有实际意义的[2].一般来讲,与环境的相互作用会导致量子体系的退相干[3]和纠缠死亡[4-5],这对应用量子纠缠实现量子信息处理是极为不利的.然而,事物大凡具有两重性,系统与环境的相互作用会破坏量子体系的纠缠,但是另一方面,环境也为两个没有直接相互作用的体系提供了间接的耦合方式.近来的研究发现,在开放系统中环境不仅可以破坏纠缠也可以诱导纠缠[6-9].这为在开放量子系统中制备纠缠开辟了新的途径.
众所周知,开放系统的动力学关键是依赖于其所耦合系统的类型[10].马尔科夫环境具有的特点是:环境的特征关联时间比系统的短的多,也就是说环境没有记忆.然而,在光子帯隙材料[11]、高Q腔系统[12]、固体系统[13]和自旋浴[14]等许多物理体系中,经常会出现非马尔科夫环境,其具有的特点是:环境的关联函数的时间尺度比系统的消相干时间尺度大几个数量级.以至于非马尔科夫环境具有明显的记忆效应,其典型特点在于其可以反馈部分信息回系统.正是由于这个原因,非马尔科夫纠缠动力学的研究越来越受到大家的重视[15-16].
在文献[6-9]中,作者们考虑了两个无相互作用的量子比特与同一个处于热平衡的马尔科夫库耦合组成的系统,研究发现环境可以诱导纠缠.然而,这样产生的纠缠只能持续很短一段时间,并且产生纠缠的最大值也很小.这就严重影响了其在量子隐形传态[1]、量子密集编码[1]和量子密码术[1]等许多量子信息处理中的应用.幸运的是,非马尔科夫环境的记忆效应提供了一个有效延长纠缠有效时间的可能途径[16-18].因此,研究非马尔科夫环境的记忆效应对诱导纠缠的影响就成了必然.文献[19]中,考虑了两个无相互作用的二能级系统与同一个非马尔科夫库非共振耦合组成的系统,研究发现,对于只含有一个激发子的两体分离态,非马尔科夫库比马尔科夫库诱导的纠缠要高得多.但是,在此系统中两个量子体系都是以纯态作为初始态,而由于量子系统与环境不可避免的相互作用,退相干和耗散都很容易使纯态演化成混合态.因此,考虑初始处于混合态的两体系统,研究非马尔科夫库诱导的纠缠是非常有意义的.
1 物理模型
在此研究无相互作用的两个量子比特系统与同一个处于零温的玻色库耦合的情况,如图1所示.整个系统的哈密顿为(h =1)
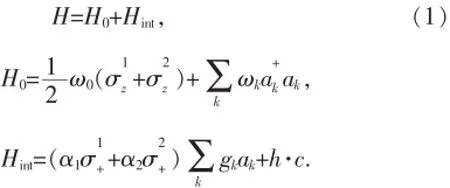
其中,ω0是两能级系统的跃迁频率,和1,2)分别为第j个量子比特的反转、上升和下降算符;和ak分别是环境库第k个模(频率为ωk)的产生和湮灭算符,gk是耦合系数.此外,第j个量子比特与库的耦合强度用无量纲的系数αj表示.
图1 物理模型示意图
如果第一个量子比特处于激发态,第二个量子比特处于基态,环境库处于真空态,即整个系统初始处于:
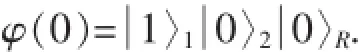
在式(1)所示哈密顿的支配下,则演化为:

文中考虑电磁场在一个中心频率为ω0的不完美光学腔中的情形,其谱密度为洛伦兹分布的形式,即:
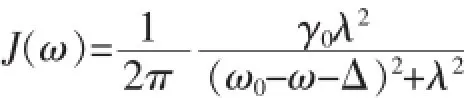
其中,Δ是跃迁频率ω0与腔中心频率之间的失谐. γ0是马尔科夫衰减系数.λ表示耦合的谱宽度,它与库的特征时间相关,即τR=λ-1.一般可以分为弱耦合和强耦合两种机制.弱耦合机制下 (γ0<λ/2),系统表现的是马尔科夫动力学伴随着不可逆的衰减;强耦合机制下(γ0>λ/2),表现的是非马尔科夫动力学伴随着振荡的可逆衰减.在此,重点讨论非马尔科夫情况.通过求解薛定谔方程可以得到:
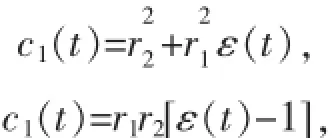

在此,令两量子比特系统初始处于:
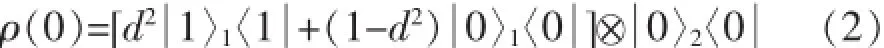
而环境库处于真空态,其中d2描述量子比特1处于激发态的布居.在式(1)所示哈密顿的支配下,系统的态演化为:
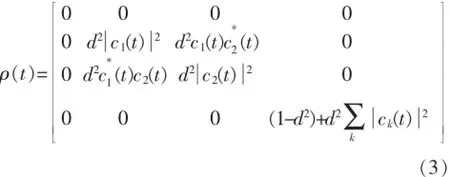
2 非马尔科夫环境诱导纠缠
为了讨论环境诱导的纠缠,在此选择concurrence[20]来量度两比特之间的纠缠.它的定义为:

其中,λi(i=1,2,3,4)是矩阵按降序排列的本征值,σy为泡利自旋矩阵,星号表示复共轭.由此,式(3)所示量子态的concurrence为:
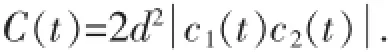
由此可以看出,系统concurrence C(t)与量子比特1处于激发态的布居d2成正比.而对于混合态而言,纯度是一个非常重要的物理参量.对于任意的量子态ρ其定义P(ρ)=tr(ρ2)[21].式(2)所示量子态的纯度为:
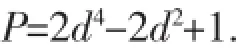
图2给出了两量子比特系统纠缠与纯度之间的关系曲线,其中α1=α2=1;λ=0.1γ0;Δ=10γ0.当d2< 0.5时,纠缠随着纯度P的增大而减小;而当d2>0.5时纠缠会随着纯度P的增大而增大.原因在于当d2<0.5时,导致纯度增大的原因是量子比特1处于基态布居的增大,而当d2>0.5时,导致纯度增大的原因是量子比特1处于激发态布居的增大.
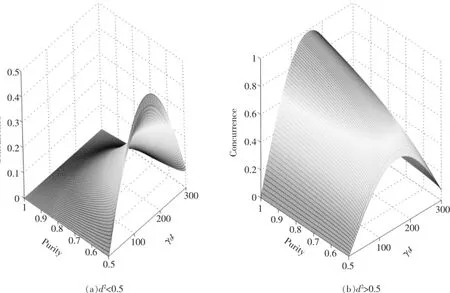
图2 系统concurrence随着初态的纯度和时间变化的曲线
另一个有趣的现象是,当量子比特系统与库非共振耦合时,非马尔科夫环境诱导的纠缠比马尔科夫环境诱导的纠缠大得多.图3给出了对于不同的失谐量,在马尔科夫和非马尔科夫机制下,诱导纠缠随着时间的变化曲线.在马尔科夫机制下,即使考虑失谐效应,环境诱导的纠缠也不足以用来完成一些量子信息处理任务.例如,利用此纠缠态将不能实现量子隐形传态,因为保真度小于2/3.然而,与马尔科夫情况不同,在非马尔科夫机制下,由耗散环境诱导的纠缠经过后趋于一个有限值,原因在于量子比特系统与非马尔科夫库之间信息的来回流动.特别是,当失谐不为零时,诱导纠缠的最大值会随着失谐量的增大而增大.其内在物理机制是非马尔科夫环境的记忆效应和系统与库的失谐抑制了像自发辐射等一些不可逆过程[17,18,22].
3结论

图3 对应于不同的失谐量Δ,环境诱导的纠缠关于无量纲量γ0t的变化曲线图
研究了无相互作用的两个量子比特系统与同一个处于零温的非马尔科夫库耦合所组成系统的纠缠动力学.结果表明,当两比特系统与非马尔科夫库非共振耦合时,可以诱导两比特间的高度纠缠.并且,非马尔科夫环境下的最大值远大于马尔科夫的情况.总之,在非马尔科夫机制下,可以通过适当的增加失谐量以获得比较高的纠缠.文中研究的模型是量子光学中的基本模型,研究结果对在开放环境中制备系统纠缠和实现量子信息处理都有重要参考价值.
[1]Nielsen M A,Chuang I L.Quantum computation and quantum information[M].United Kingdom:Cambridge University Press,2010.
[2]Breuer H P,Petruccione F.The theory of open quantum systems[M]. New York:Oxford University Press,2002.
[3]Zurek W H.Decoherence,einselection,and the quantum origins of the classical[J].Reviews of Modern Physics,2003,75(3):715-775.
[4]Yu T,Eberly J H.Finite-time disentanglement via spontaneous emission[J].Physical Review Letters,2004,93:140404.
[5]Yu T,Eberly J H.Sudden death of entanglement[J].Science,2009, 323(5914):598-601.
[6]Braun D.Creation of entanglement by interaction with a common heat bath[J].Physical Review Letters,2002,89(27):277901.
[7]Kim M S,Lee J,Ahn D,et al.Entanglement induced by a singlemode heat environment[J].Physical Review A,2002,65(4):040101.
[8]BenattiF,FloreaniniR,PianiM.Environmentinduced entanglement in Markovian dissipative dynamics[J].Physical Review Letters,2003,91:070402.
[9]Nicolosi S,Napoli A,Messina A,et al.Dissipation-induced stationaryentanglementin dipole-dipoleinteractingatomic samples[J].Physical Review A,2004,70(2):022511.
[10]Gardiner C W,Zoller P.Quantum Noise[M].Berlin:Springer, 1999.
[11]Piilo J,Maniscalco S,Ha¨rko¨nen K,et al.Non-Markovian quantum jumps[J].Physical Review Letters,2008,100(18):180402.
[12]Dubin F,Rotter D,Mukherjee M,et al.Photon correlation vs interference of single-atom fluorescence in a half-cavity[J]. Physical Review Letters,2007,98:183003.
[13]Lai C W,Maletinsky P,Badolato A,et al.Knight-field-enabled nuclear spin polarization in single quantum dots[J].Physical Review Letters,2006,96(16):167403.
[14]Burkard G.Non-Markovian qubit dynamics in the presence of 1/f noise[J].Physical Review B,2009,79(12):125317.
[15]Bellomo B,Franco R L,Compagno G.Non-Markovian effects on the dynamics of entanglement[J].Physical Review Letters,2007, 99(16):160502.
[16]Bellomo B,Franco R L,Maniscalco S,et al.Entanglement trapping in structured environments[J].Physical Review A,2008, 78(6):060302.
[17]Maniscalco S,Francica F,Zaffino R L,et al.Protecting entanglement via the quantum Zeno effect[J].Physical Review Letters,2007,99:160502.
[18]Xiao X,Fang M F,Li Y L,et al.Robust entanglement preserving by detuning in non-Markovian regime[J].Journal of Physics B: Atomic,Molecular and Optical Physics,2009,42(23):235502.
[19]Li Y L,Fang M F.High entanglement generation and high fidelity quantum state transfer in a non-Markovian environment [J].Chinese Physics B,2011,20(10):100312.
[20]Wootters W K.Entanglement of formation of an arbitrary state of two qubits[J].Physical Review Letters,1998,80(10):2245.
[21]Rossatto D Z,Werlang T,Castelano L K,et al.Purity as a witness for initial system-environment correlations in open-system dynamics[J].Physical Review A,2011,84(4):042113.
[22]Huang L Y,Fang M F.Protecting entanglement by detuning:in Markovian environments vs in non-Markovian environments[J]. Chinese Physics B,2010,19(9):090318.
Purity dependence of entanglement generation in non-Markovian environment
LI Yan-ling,XU Zhong-hui,HUO Liang(Faculty of Information Engineering,Jiangxi University of Science and Technology,Ganzhou 341000,China)
We consider the model of two uncoupled qubits system interacting with a common zero-temperature non-Markovian reservoir.For an initially factorized two-qubit mixed state,the entanglement can be induced by non-Markovian environment.And its value is highly dependent on the initial purity of the system.Moreover, the entanglement induced by non-Markovian reservoir is much larger than that induced by Markovian reservoir.The maximal value of the induced entanglement increases with the increasing of detuning.The study shows that highly entangled states which are essential to implement some quantum information processing,can be induced by increasing the detuning between the system and the non-Markovian reservoir.
non-Markovian environment;induced entanglement;purity
O431.2
A
2095-3041(2014)00-0090-04
10.13265/j.cnki.jxlgdxxb.2014.01.015
2013-07-17
国家自然科学基金理论物理专项(11247207);江西理工大学科研基金项目(jxxj12056)
李艳玲(1981- ),女,博士,讲师,主要从事量子光学和量子信息等方面的研究,E-mail:liyanling0423@gmail.com.
