利用数控机床换向特性分析的摩擦误差补偿方法

牟恩旭，马振群，冯 斌，任建功

（西安交通大学机械工程学院，710049，西安）

摩擦是一种广泛存在于机械动静接触面之间的自然现象［1］。当数控机床运行至换向处时，摩擦力矩方向突变所产生的非线性干扰会使控制系统产生较大的运动误差［2］。为提高数控机床的运动精度，许多学者针对数控机床伺服进给系统摩擦误差补偿开展了研究工作。目前的补偿方法可以分为基于摩擦模型的补偿和基于前馈脉冲的补偿。前者主要对伺服进给系统在运动过程中的摩擦力矩进行建模，并根据摩擦模型在电流环施加补偿力矩实现补偿。在摩擦模型的研究中比较著名的有Stribeck模型、Dahl模型及LuGre模型等［3-4］。上述模型从不同角度对动静接触面之间的摩擦特性进行了描述，但由于影响数控机床伺服进给系统摩擦特性的因素众多，如温度、接触面润滑情况、接触面表面质量等因素的变化均会改变动静接触面间的摩擦特性［5］，仍难以获得准确的摩擦模型。此外，由于大部分摩擦模型表达式复杂以及受到系统开放性的限制，电流环直接补偿的方式在实际数控系统中难以实现，因此在工程应用中多采用基于前馈脉冲的补偿方法。

基于前馈脉冲补偿方法的补偿原理为在伺服进给系统运动至换向位置时，在控制环路中加入补偿脉冲，以抵消摩擦对运动的影响［6］。由于在控制器电流环施加补偿脉冲易对伺服进给系统产生冲击，且受到数控系统开放性限制，因此多将补偿脉冲施加于位置环或速度环。目前，商用数控系统中主要依靠人工经验调整补偿脉冲参数，确定合理的补偿参数较为困难。为实现摩擦误差补偿的自动化与智能化，Tung等提出通过重复控制器获得补偿脉冲参数的方法［7］，但因其需要改变控制器结构，具有在数控系统中可行性不强的缺点；陈光胜等提出了一种双脉冲补偿方法，并给出了补偿脉冲参数计算方法［8］，但其为快速推动工作台运动使用了矩形脉冲，具有易对工作台产生冲击的缺点；冯斌等通过对摩擦补偿参数进行在线学习，获得了摩擦补偿脉冲参数［9］，但由于未能充分利用伺服进给系统换向处特性，存在寻优范围大，学习时间长等不足。

本文对伺服进给系统换向处动态特性进行了分析，并根据补偿脉冲对伺服进给系统运动状态的影响，确定了合理补偿脉冲参数的准则。基于该准则，提出了一种确定三角形摩擦误差补偿脉冲参数的方法，并在自主开发的开放式数控系统平台上进行了摩擦误差补偿实验。实验结果表明，本文方法能够有效地减小伺服进给系统换向处误差，证明了本文方法的有效性及可行性。

1 换向处动态特性分析

为分析伺服进给系统换向处的动态特性，在搭建的开放式数控系统平台上进行了相关实验。该平台由高性能伺服电机、驱动器及开放式数控系统组成，并采用高分辨力光栅尺进行全闭环运动控制，其机械部分为基于立式铣床改造的X-Y精密工作台。该精密工作台作为典型伺服进给系统，其在换向处的摩擦特性主要表现为在工作台运动换向时，摩擦力矩方向发生突变［3］。图1显示了在未补偿条件下，在开放式数控系统平台上运行半径为25mm、进给速度为1m／min的圆轨迹时，工作台X轴位置误差、实际速度及力矩电压指令信号的变化情况。

由图1可知，在到达换向时刻ta前，工作台位置误差、实际速度及力矩电压指令处于正常状态。在ta时刻后，工作台实际速度为0，进入停驻状态。此后，工作台位置误差开始逐渐增加，由于误差的不断累积，力矩电压指令不断增大。当力矩电压指令所产生的力矩大于能使工作台运动的分离力矩Tb时，工作台开始运动，将此时的力矩电压指令值称为分离电压Vb，将该时刻称为分离时刻tb。当工作台开始运动后，由于实际运动速度小于指令速度，位置误差继续增大，力矩电压指令也随之增大，工作台加速运行。当到达tp时刻时，工作台实际速度等于指令速度，此时位置误差达到峰值。之后，伺服控制系统为减小位置误差不断进行调整，造成力矩电压指令及实际速度出现波动，位置误差逐渐减小。在时刻tc时，位置误差值恢复至正常运行范围，伺服控制系统完成对换向处摩擦影响的调整。

2 摩擦误差补偿原理及补偿状态分析

为确定合理补偿脉冲参数，本节将结合运动控制模型，分析补偿脉冲对工作台动态特性造成的影响。

2.1 摩擦误差补偿原理

图2为数控机床控制中常见的控制器结构，其采用三环PID控制方法，位置环为P控制器，速度环为PI控制器。其中位置环比例增益为Kpp，速度环比例增益为Kvp，速度环积分增益为Kvi，系统的电流环由于带宽较高，可等效为比例环节，其比例系数为。考虑到速度环响应速度较位置环高，本文将补偿脉冲施加于速度环处，即图2中A位置。

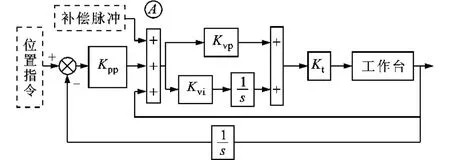
图2 伺服进给系统控制器结构

相比于矩形脉冲，三角形补偿脉冲能够减小对系统的冲击且补偿效果更好，本文采用三角形补偿脉冲对摩擦误差进行补偿。三角形补偿脉冲示意图如图3所示，其中Pmax为脉冲峰值，t1与t2分别为补偿时间参数1与补偿时间参数2，图中的横轴起点为工作台到达换向点时刻。为表述方便，在分析脉冲形态时以该时刻为零时刻点。

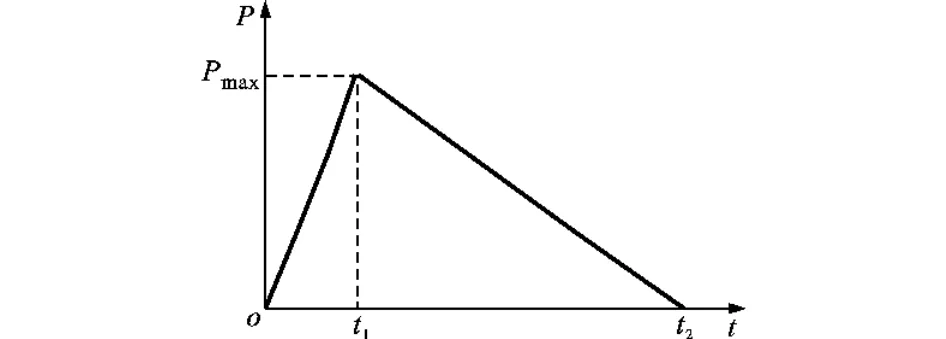
图3 三角形补偿脉冲形态示意图

由图3可知，三角形补偿脉冲的形态函数fvc（t）表达式为

由速度环加入的补偿脉冲，经速度控制器转变为力矩电压指令，其函数表达式为

对式（3）求导，可得

由式（4）可知，对于图3中的三角形脉冲，由于Kvp、Kvi、Pmax、t1各项均为正值，fval（t）在t∈［0，t1）上单调递增。当t∈（t1，t2］时，由于

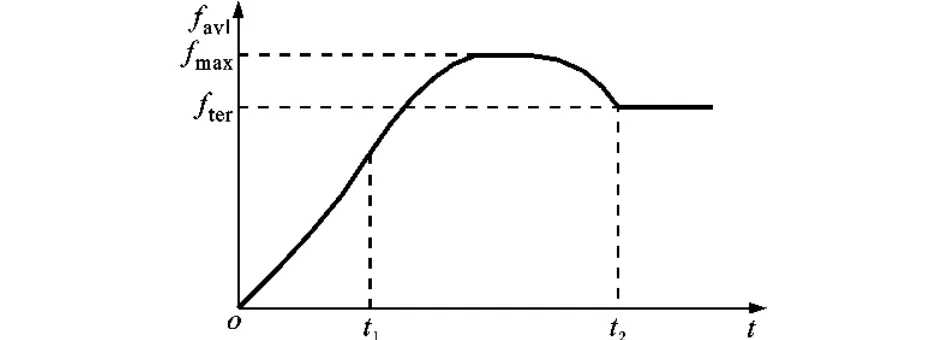
图4 函数fval（t）的示意图

通过以上分析可以发现，无论脉冲参数Pmax、t1和t2如何取值，其所产生的力矩指令电压都会有一个先增后减的变化过程。下文将结合实验说明不同参数下的补偿脉冲对补偿效果产生的影响。

2.2 不同参数补偿脉冲作用下换向处特性分析

为便于分析及叙述，本文依据工作台在换向处位置误差形态，将工作台在不同补偿脉冲作用下的补偿状态分为3类。将补偿后位置误差绝对值在一较小范围内的情况称为理想补偿。若位置误差超出该范围，且其尖峰方向同未补偿时方向相同，则称为欠补偿。在欠补偿状态下，若位置误差出现两个尖峰，本文称其为欠补偿A状态，而对于位置误差只有一个尖峰的情况，则称之为欠补偿B状态，如图5a所示。若位置误差超出该范围，但其尖峰方向与未补偿时相反，则称为过补偿。在过补偿条件下，同样会出现位置误差呈现双尖峰的情况，与欠补偿A状态下不同，此时两个位置误差尖峰的方向相反。本文将过补偿状态下位置误差出现两个尖峰的情况定义为过补偿A状态，而将过补偿状态下位置误差只有一个尖峰的情况定义为过补偿B状态，如图5b所示。

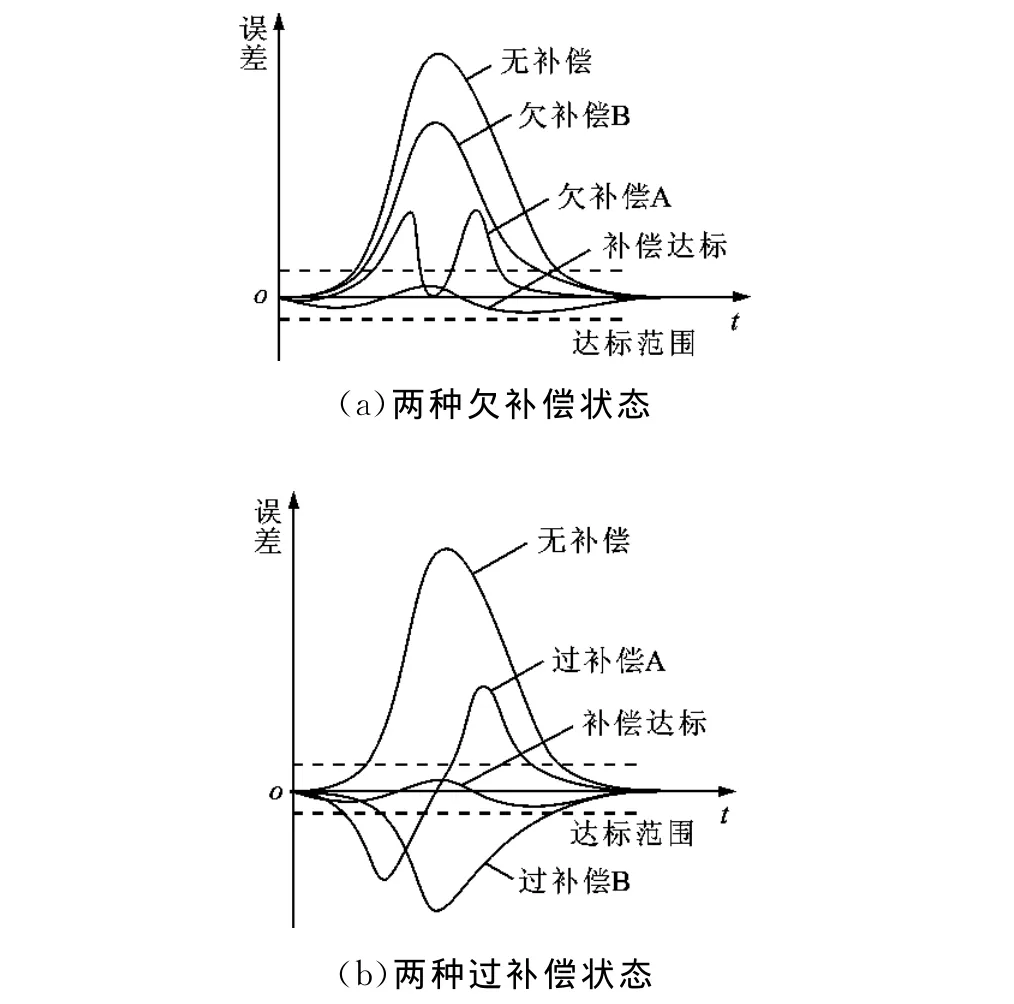
图5 补偿状态示意图

本文采集了工作台X轴在进给速度为1m／min、半径为25mm时，换向处的位置误差、实际速度及力矩电压指令信息。通过对以上信息进行对比，分析了不同参数补偿脉冲作用下工作台在换向处的动态特性。

通过观察图6可知，在理想补偿状态下，工作台位置误差无尖峰存在，力矩电压指令以较快的速度上升，然后趋于平缓，工作台实际速度均匀增加。这说明在补偿脉冲的作用下，工作台处于停驻状态的时间较短，且速度上升平稳。

图6同时显示了工作台的两种欠补偿状态。从图6a可以看出，在欠补偿A状态下，工作台位置误差出现两个尖峰。综合图6b的实际速度信号可以发现，在此状态下，由于补偿脉冲的作用，工作台在到达换向点后很快脱离了停驻状态。当在脱离停驻状态一段时间后，其实际速度再次为0，工作台再次进入停驻状态。通过观察图6c的力矩电压指令信号可以发现，由于补偿脉冲参数设置不合理，补偿脉冲产生的力矩电压指令在上升后，出现了较为明显的下降。当力矩电压指令所产生的力矩小于摩擦力矩时，工作台再次发生停驻。此后，由于误差的累积，力矩电压指令再次增大，工作台在经历了一段时间的停驻后再次开始运动。在此过程中，工作台经历了停驻-运动-停驻-运动的过程，造成了位置误差曲线中的两个误差尖峰。

在欠补偿B状态下，通过观察实际速度曲线可以发现，同无补偿状态一样，工作台经历了停驻-运动的过程。但是，在补偿脉冲作用下，力矩电压指令变化较无补偿状态下快，而较理想补偿状态下慢，因此其对换向误差的补偿作用不及使工作台处于理想补偿状态下的补偿脉冲。相比于欠补偿A状态，力矩电压指令下降不明显，其所产生的力矩能够维持工作台持续运动，未使工作台出现再次进入停驻状态的情况。

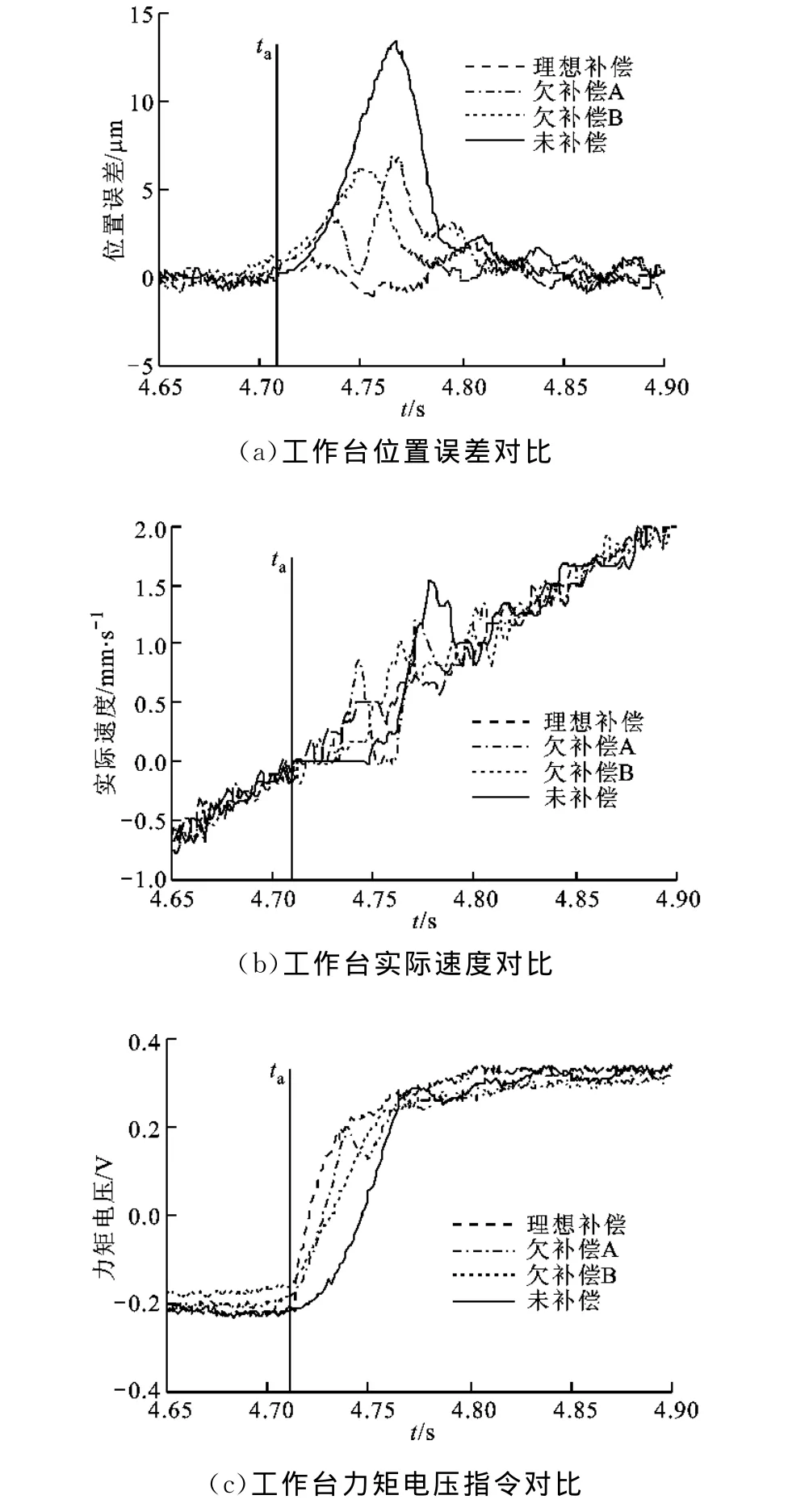
图6 欠补偿状态下工作台运动信息对比

图7 显示了工作台在过补偿A状态下的动态特性。通过观察其实际速度曲线可以发现，工作台如在欠补偿A状态下一样经历了停驻-运动-停驻-运动的过程，其原因与前述相同，这里不再赘述。同样，对于过补偿B状态，工作台如在欠补偿B状态下一样经历了停驻-运动的过程。但是，由于在过补偿状态下，补偿脉冲幅值大且变化快，引起力矩电压指令在开始阶段急剧增大，使实际运动速度大于指令速度，从而形成了与欠补偿情况下方向相反的位置误差，产生了所谓的“过切”现象。过切现象会导致所加工工件产生无法弥补的后果，且会使刀具加速磨损乃至直接损坏［11］，因此在实际补偿中应尽量避免发生过补偿现象。

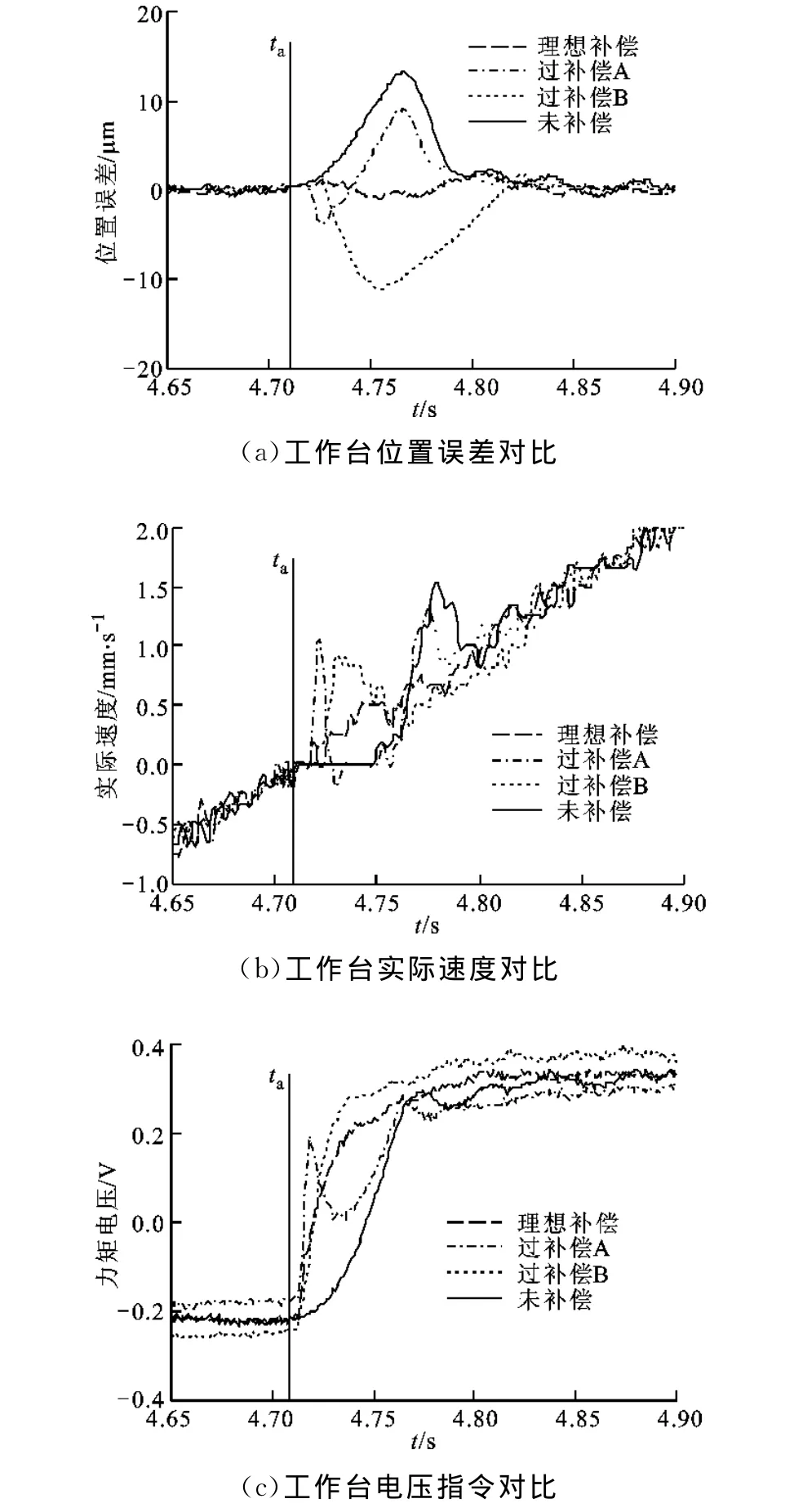
图7 过补偿状态下工作台运动信息对比

3 三角形补偿脉冲参数的确定

3.1 合理补偿脉冲参数

（1）在补偿开始阶段，补偿脉冲应使力矩电压指令以适当的速率上升并达到分离电压Vb，从而使工作台脱离停驻状态，即

式中：Va为换向点处力矩电压指令值；ts为加入补偿脉冲后的分离时刻。

（2）在补偿结束的t2时刻，补偿脉冲所产生力矩电压指令终值fval（t2）应使工作台的驱动力矩至少等于其阻力矩，以保证工作台不会再次进入停驻状态。同时，为了不使t2时刻实际运动速度超过速度指令，令t2时刻工作台力矩电压指令等于无补偿时系统调整结束tc时刻的力矩电压指令Vc，即

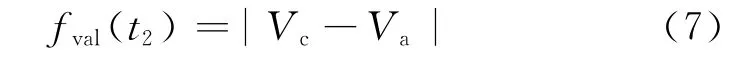
3.2 合理补偿脉冲参数计算方法

在数控系统中，计算合理补偿脉冲参数所需信息，可通过以下方法获取。

（1）在未补偿条件下，使工作台以特定轨迹运行，获得工作台在无补偿条件下换向处的位置反馈曲线、位置误差曲线及力矩电压指令曲线。对位置反馈曲线进行差分及平滑处理，获得实际速度曲线。通过实际速度曲线确定换向时刻ta、未补偿时分离时刻tb，通过位置误差曲线确定调整完成时刻tc。在力矩电压指令曲线上读出ta、tb、tc时刻对应的力矩电压指令Va、Vb、Vc。

（2）为使工作台能较快脱离停驻状态，将ts取值为

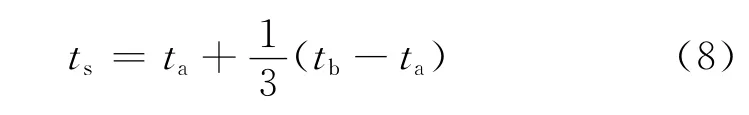
（3）根据上文所总结的合理补偿脉冲参数来确定准则，联立式（3）、式（6）与式（7），可得

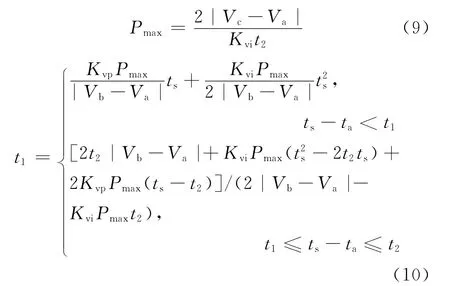
为使补偿脉冲所产生力矩电压指令尽量平缓，避免引起系统振荡，应使t2的取值尽量大，这里根据无补偿情况下的稳定时间确定t2

由于在实际中，工作台在各位置的摩擦特性不尽相同，因此在一处获得的合理补偿脉冲参数未必能适用于全行程。为避免在个别位置出现过补偿现象，实际中应选用的补偿参数可根据补偿效果进行调整，可将实际选用的补偿脉冲峰值定为

式中：δ为调整系数，取值为［0.8，1］。

4 验证实验

为验证本文所提出方法的有效性，在开发的开放式数控系统平台上进行摩擦误差补偿实验。

控制精密工作台X轴先后以进给速度F为1m／min和3m／min、运行幅值为25cm的正弦轨迹，根据上文介绍方法采集所需要的相关参数。在一个运动周期中，工作台经历两个换向点，这里将力矩电压信号由负变为正的方向记为C向，反之记为D向。由于机械结构存在装配水平度差等缺陷，C向与D向的摩擦特性存在较明显的差异。为了方便记述，将ta时刻记为0，各参数实测值如表1所示。

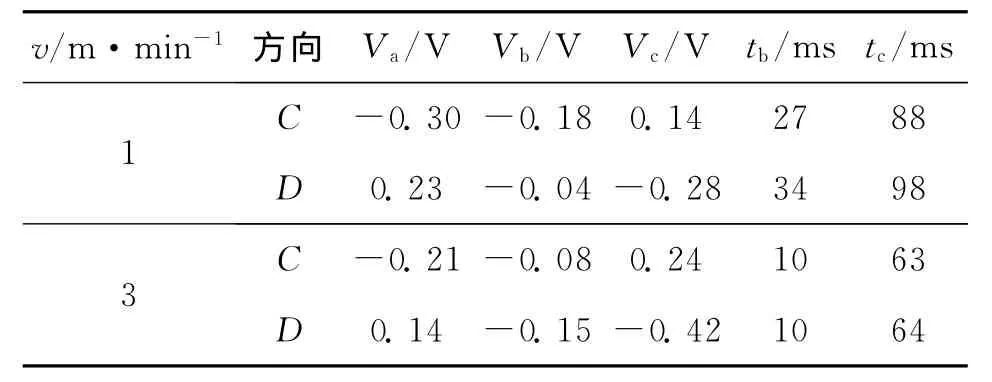
表1 无补偿状态下实测参数值

实际控制器Kvp为0.06，Kvi为5，取δ为1。将表1中的数据代入式（8）～式（12），计算得到在不同速度下补偿脉冲所应选取的参数，见表2。

表2 摩擦误差补偿脉冲参数计算值

将设置好的补偿脉冲施加至图2所示A位置，在1m／min和3m／min进给速度下验证补偿效果，实验结果如图8所示。为了对实验结果进行量化分析，对从换向时刻开始的监测时间tM内的跟随误差进行监测，并采用绝对误差尖峰及绝对误差平均值对补偿效果进行综合评价。tM值根据各工况换向过程所需的时间进行设定，这里tM取为150ms。表3中列出了不同进给速度下补偿前后监测时间tM内绝对误差最大值P及其平均值M 的数值。综合图8及表3可以发现，本文方法在不同工况下均能有效减小工作台换向处误差，获得较理想的补偿效果。

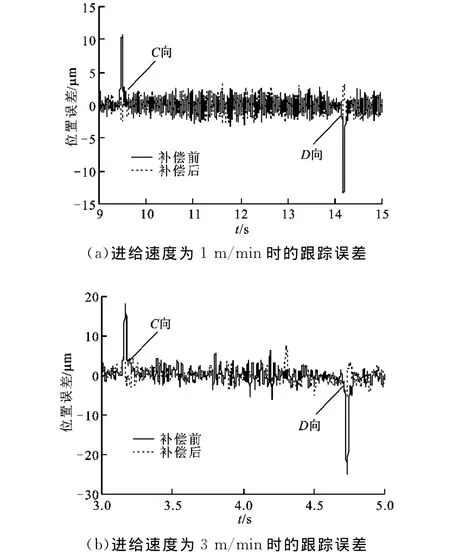
图8 摩擦误差补偿效果对比

表3 摩擦误差补偿效果综合评价表

5 结 论

（1）针对工业实际中难以确定数控机床摩擦误差补偿脉冲参数的问题，本文提出了一种基于数控机床换向特性分析的摩擦误差补偿方法。该方法通过获得工作台在无补偿状态下的相关信息，根据所提出的合理脉冲参数确定准则及计算公式对三角形补偿脉冲的参数进行计算。由于充分利用了伺服进给系统换向处的特性，实现了对补偿脉冲参数的直接计算，大幅提高了调试效率。

（2）分析了伺服进给系统在换向处的动态特性。结合实际补偿实验数据及对补偿脉冲形态的推导，分析了补偿脉冲对工作台换向处动态特性的影响。根据分析结果，总结了合理补偿脉冲参数以确定准则。

（3）在X-Y精密工作台的X轴上以不同进给速度进行了摩擦误差补偿实验。实验结果表明，该方法在不同工况下均能有效减小换向处绝对误差尖峰值及绝对误差均值，其对换向处误差尖峰值的抑制达到70%以上，对换向处误差平均值的抑制达到50%以上，验证了该方法的可行性及有效性。

［1］ OLSSON H，ÅSTRÖM K J，DE WIT C C， et al.Friction models and friction compensation ［J］.European Journal of Control，1998，4（3）：176-195.

［2］ EUN-CHAN P，HYUK L，CHONG-HO C.Position control of X-Y table at velocity reversal using presliding friction characteristics ［J］.IEEE Transactions on Control Systems Technology，2003，11（1）：24-31.

［3］ ARMSTRONG-HÉLOUVRY B， DUPONT P，DE WIT C C.A survey of models，analysis tools and compensation methods for the control of machines with friction［J］.Automatica，1994，30（7）：1083-1138.

［4］ SYH-SHIUH Y，HSIN-CHUN S.Development of friction identification methods for feed drives of CNC machine tools［J］.International Journal of Advanced Manufacturing Technology，2011，52（1／2／3／4）：263-278.

［5］ HSIEH C，PAN Y C.Dynamic behavior and modelling of the pre-sliding static friction［J］.Wear，2000，242（1／2）：1-17.

［6］ MEI X S，TSUTSUMI M，TAO T，et al.Study on the compensation of error by stick-slip for highprecision table ［J］.International Journal of Machine Tools ＆ Manufacture，2004，44（5）：503-510.

［7］ TUNG E D，ANWAR G，TOMIZUKA M.Low-velocity friction compensation and feedforward solution based on repetitive control［J］.ASME Journal of Dynamic Systems Measurement and Control，1993，115（2A）：279-284.

［8］ 陈光胜，梅雪松，陶涛.X-Y工作台摩擦误差补偿方法的研究 ［J］.西安交通大学学报，2011，45（1）：69-73.

CHEN Guangsheng，MEI Xuesong，TAO Tao.Compensation of friction error for X-Ytable［J］.Journal of Xi’an Jiaotong University，2011，45（1）：69-73.

［9］ 冯斌，梅雪松，杨军，等.数控机床摩擦误差自适应补偿方法研究 ［J］.西安交通大学学报，2013，47（11）：65-69.

FENG Bin， MEI Xuesong， YANG Jun，et al.Adaptive compensation of friction error for numerical control machine tool［J］.Journal of Xi’an Jiaotong University，2013，47（11）：65-69.

［10］KIM M S，CHUNG S C.Integrated design methodology of ball-screw driven servomechanisms with discrete controllers：part I modelling and performance analysis［J］.Mechatronics，2006，16（8）：491-502.

［11］ELLIS G.Control system design guide［M］.San Diego，USA：Elsevier Academic Press，2004：51-52.

［本刊相关文献链接］

冯斌，梅雪松，杨军，等.数控机床摩擦误差自适应补偿方法研究.2013，47（11）：65-69.［doi：10.7652／xjtuxb201311012］

李学伟，赵万华，卢秉恒.轨迹误差建模的多轴联动机床轮廓误 差 补 偿 技 术.2012，46（3）：47-52.［doi：10.7652／xjtuxb 201203009］

马晓龙，陈贵灿.固定位宽乘法器的量化误差补偿方法及电路实 现.2011，45（12）：75-81.［doi：10.7652／xjtuxb201112 014］

陈光胜，梅雪松，陶涛.X-Y工作台摩擦误差补偿方法的研究.2011，45（1）：69-73.［doi：10.7652／xjtuxb201101014］

周玉清，陶涛，梅雪松，等.旋转轴与平移轴联动误差的快速测量及溯源.2010，44（5）：80-84.［doi：10.7652／xjtuxb201005 017］

李彪，刘新正，李黎川.具有低通滤波的改进电压型磁链观测器.2009，43（12）：91-95.［doi：10.7652／xjtuxb200912019］

韦进文，郭俊杰.坐标测量机动力学刚度估计与加速度误差补偿.2009，43（1）：47-51.［doi：10.7652／xjtuxb200901011］

丁建军，蒋庄德，李兵，等.线结构光扫描测头误差分析与补偿方法.2008，42（3）：286-290.［doi：10.7652／xjtuxb200803 007］

刘保华，李兵，崔希君，等.一种多线结构光测头的误差补偿方法.2007，41（1）：50-54.［doi：10.7652／xjtuxb200701012］