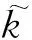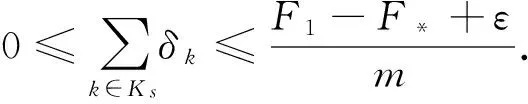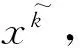一类联合最大特征值函数优化问题
2014-01-15李尚华
王 炜,陈 渺,李尚华
(辽宁师范大学 数学学院,辽宁 大连 116029)
0 引言
1 目标函数的近似
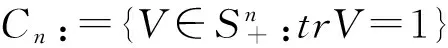
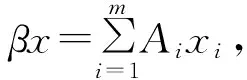
设F(y)=λmax(A(y))+g(y),Y∈Rn,假设
ri(domλmax(A(y)))∩ri(domg(y))≠φ,
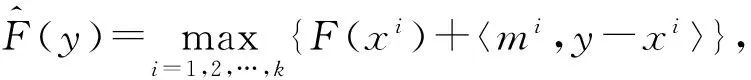
β*Q(A(xi))ZQ(A(xi))T+si∈∂λmax(A(xi))+∂g(xi)=∂[λmaxA(xi)+g(xi)],
于是有
令线性化误差
ei=F(xk)-F(xi)-〈β*Q(A(xi))ZQ(A(xi))T+si,xk-xi〉,
得F(y)的近似的具体形式为

2 带有罚项的束方法算法
求解问题的(P)带有罚项的束方法的算法
Step 0 令ε≥0,m∈(0,1)为给定参数,选定x1,运用黑盒子得到F(x1)和β*Q(A(x1))ZQ(A(x1))T+s1∈∂[λmaxA(x1)+g(x1)],构造模型F1,令k=1,δ1=∞.
Step 1 若δk≤ε,则停止算法.
Step 2 求解
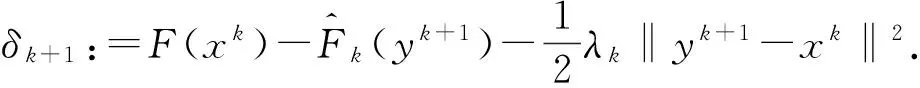
Step 3 将点x=yk+1代入黑盒子中,考察是否有
F(xk)-F(yk+1)≥mδk+1
(2.1)
若(2.1)成立,取xk+1=yk+1,并称为下降步;若(2.1)不成立,取xk+1=xk,并称为零步.
Step 4 添加yk+1至模型中,构造Fk+1,令k=k+1,回Step 1.
在Step 2 中,候选点yk+1可通过求(P1)的对偶问题得到,具体由以下定理所保证.
定理2.1若yk+1为(P1)的唯一解,则
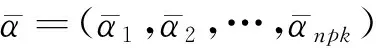
的解,此外,还可以得到以下结论:
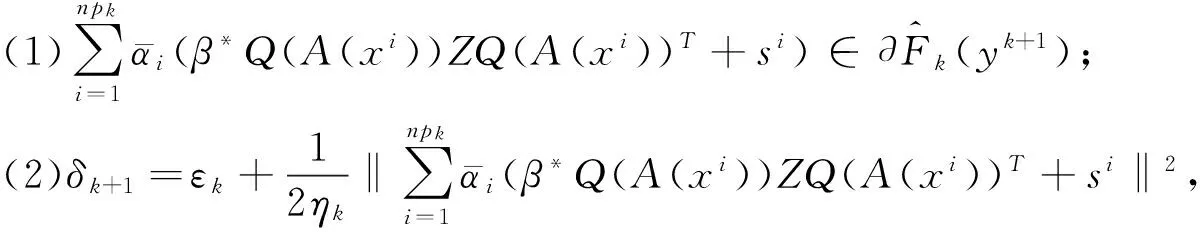
证明引入辅助变量r,(P1)等价于
npk(P2)的Lagrangian为
〈β*Q(A(xi))ZQ(A(xi))T+si,y-xk〉-r),
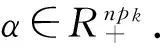
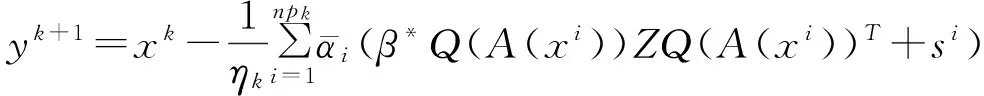
为(P1)的解,所以(1)成立.
通过(P1)与(P1)的对偶问题的最优解均为yk+1,易知(2)成立.

在迭代过程中,束中的元素会不断增加,此时,需要压缩机制来控制束的大小.当束中当前元素量npk超过束中可允许的最大元素量npmax时,Step 4变为如下形式:
若nact≤npmax-1,则删除不积极的指标,nleft=nact,定义npk+1=nleft+1,然后,把(β*Q(A(xnpk+1))ZQ(A(xnpk+1))T+snpk+1,enpk+1)放入束中,其中

若nact>npmax-1,则删除不积极的指标,且去掉两个或多个元素(β*Q(A(xi))ZQ(A(xi))T+si,ei),将去掉的两个或多个元素合成(即合成束,见注1).此时,nleft=npmax-2或nleft 构造Fk+1,令k=k+1,返回Step 1. 注1:当束中当前元素量npk超过束中可允许的最大元素量npmax时,将不积极的元素删除,若余下的元素仍太多,则将必不可少的元素合成.即利用由定理2.1得到的 构造集合线性化函数Fα(y): Fα(y)有如下性质: 注2:当束中元素量超过束中可允许的最大值npmax时,假设决定去掉x1,x2,…,xt,则新的模型为 假设停止准则为δk+1≤ε,我们分ε>0为ε=0和两方面进行分析. 证明由于算法无限循环及ε≥0知δk>0,而k∈Ks,则xk+1=yk+1,则F(xk)-F(xk+1)≥0,令k′为Ks中k的下一个指标k且k′与之间存在零步,则j=2,3,…,k′-k时不用移动稳定中心.即xk+1=xk+j且F(xk+1)-F(Xk′+1)=mδk′+1,则对∀k′∈Ks,∀ε>0,有 当k″→∞时,结论成立. 证毕. 情况1.Ks中有无限元素 以下定理保证了以上两种情况下算法的收敛性(证明过程类似于[4]). 定理3.2假设算法产生无限下降步xk,则下列两种情况必有一种成立. (i)原问题无最优解且{F(xk)}递减趋近于-∞; (ii)原问题有最优解,此时,若k∈Ks,k→-∞,有{δK}→0且{εk}→0,若0<ηk+1<ηk,则{xk}有界且收敛于原问题的最小值点. [1] Christoph Helmberg,Francois Oustry.Bundle methods to minimize the maximum eigenvalue function[J].Handbook of Semidefinite Progamming,2000,27:307~337. [2]Claudia Sagastizabal,Mikhail Solodov.An infeasible bundle method for nonsmooth convex constrained optimization without a penalty function or filter[J].SIAM J.Optimization,2005,16(1):146~169. [3]Oustry F.,Lemarchal C.Nonsmooth algorithms to solve semidefinite programs[J].Society for Industrial and Applied Mathematics Philadelphia,2000,57~77. [4]J.Frederic Bonnans,J.Charles Gilbert,Claude Lemarechal,et al.Sagatizabal.Bundle methods.The quest of descent.Numerical Optimization,2003,117~136. [5]周茂袁,王秀丽,李雪艳.特征函数的一种新解释及其应用[J].吉林师范大学学报(自然科学版),2008,29(2):45~48. [6]初 丽.线性互补问题的序列凸近似方法[J].吉林师范大学学报(自然科学版),2013,34(4):117~120. [7]Claudia Sagastizábal,Mikhail Solodov.An infeasible bundle method for nonsmooth convex constrained optimization without a penalty function or filter[J].SIAM J.Optimization,2005,16(1):146~169. [8]Ladislav Lukgan,Jan Vicek.A bundle-Newton method for nonsmooth unconstrained minimization[J].The Mathematical Programming Society,1998,373~391. [9]Antonio Frangioni.Generalized bundle methods[J].SIAM J.OPTIM,2001,13(1):117~156. [10]L.Lukšan,J.Vicek.Globally Convergent Variable Metric Method for Convex Nonsmooth Unconstrained Minimization.Journal of optimization theory and applications,1999,102(3):593~613. [11]K.Kiwiel.A bundle Bregman proximal method for convex nondifferentiable optimization,Math.Program.,1999,85,241~258.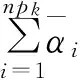
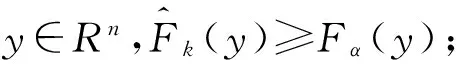

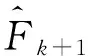
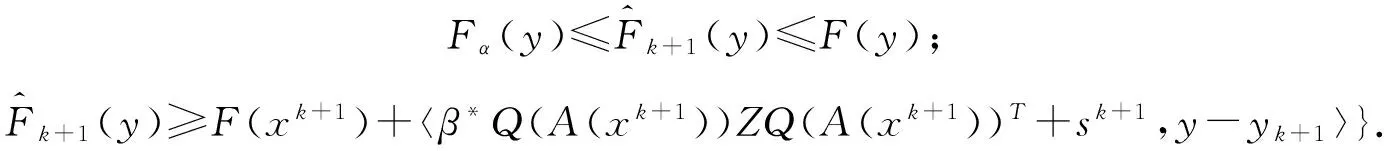
3 收敛分析