页岩储集层微观渗流的微尺度效应
2014-01-15宁正福王波杨峰曾彦陈进娥张廉
宁正福,王波,杨峰,曾彦,陈进娥,张廉
(1. 中国石油大学(北京)石油工程教育部重点实验室;2. 中国石油大学(北京)油气资源与探测国家重点实验室;3. 东方地球物理公司研究院)
0 引言
页岩储集层孔隙结构复杂,非均质性严重,孔隙尺寸多为纳米—微米数量级,并且具有很强的多尺度性[1]。纳米级孔隙多存在于页岩有机质中,因此研究气体在页岩有机质中的流动对探讨页岩气的渗流规律、正确预测页岩气的产能具有重要意义[2-4]。
当气体在有机质中的运动空间减小到一定程度,其流动规律明显不同于在常规尺度空间中的流动,即存在微尺度效应。Roy等[5]根据 Knudsen数(Kn)的取值划分了4个流动区域:①连续介质区,Kn≤0.001,气体服从达西定律,属连续介质流;②滑移区,0.001
作为一种介观数值模拟方法,格子 Boltzmann方法具有简单、并行、高效的特点。为研究页岩有机质中气体的流动机理及影响因素,本文运用格子Boltzmann方法,采用Langmuir边界条件模拟气体在有机质纳米孔道中的流动,分析页岩气流动的微尺度效应及其对渗流的影响。
1 页岩储集层的纳米级孔隙
页岩样品采自四川盆地下寒武统牛蹄塘组。牛蹄塘组页岩属海相沉积环境的黑色炭质泥页岩,有机质丰度高,总有机碳含量为 3.68%~9.15%,平均为6.25%;有机质成熟度为 1.8%~2.7%,已达到高熟或过成熟阶段。观察仪器采用FEI Quanta 200F场发射扫描电子显微镜,该扫描电镜分辨率可达1.2 nm,放大倍数25 000~200 000。为了便于观察,应用氩离子抛光技术对样品进行处理,用高速离子束轰击样品表面,避免了机械抛光对样品表面的破坏,并且真实保留了样品表面的孔隙形态。观察发现页岩样品中存在大量纳米级孔隙。
在页岩样品中取一小块岩石碎块,在碎块中切一薄片,进行扫描电镜实验,然后重构页岩多孔介质模型,进而进行数字化分析;将碎块中其余部分磨成粉末状,进行氮气吸附实验;在样品中相邻位置钻取一圆柱状小岩心,进行高压压汞实验。3种实验方法得到的孔径分布见图1,可见孔隙大小为纳米量级,样品中有机质纳米孔半径多为5~150 nm。
对于宏观流体流动,通常采用经典N-S方程描述,但对于纳米级孔隙,由于孔隙特征长度与流体分子的平均分子自由程相当,所以流体连续性假设不成立,无滑移边界条件的 N-S方程也不成立,需要引入Knudsen数Kn(分子平均自由程与流动通道特征尺寸之比[15])描述微尺度流动。其中,气体分子平均自由程计算公式为:

图1 页岩孔径分布

常温常压下甲烷气体的平均分子自由程为 53.1 nm,假设储集层条件为60~80 ℃、30~60 MPa,则甲烷气体的平均分子自由程为0.9~1.8 nm[16-17]。根据Knudsen数定义[15]可知,有机质中甲烷气体流动的Knudsen数为0.006~0.180,属于滑移区和弱过渡区。
2 页岩储集层微观渗流的格子Boltzmann模拟
2.1 计算模型
本文采用格子 Boltzmann-BGK[15]方程 D2Q9(二维九速)模型,对图 2所示二维纳米孔道中甲烷气体的流动进行数值模拟。
通过BGK近似[18]、时空离散和速度离散,得到完全离散化的格子Boltzmann-BGK方程(LBM)[15,18]:
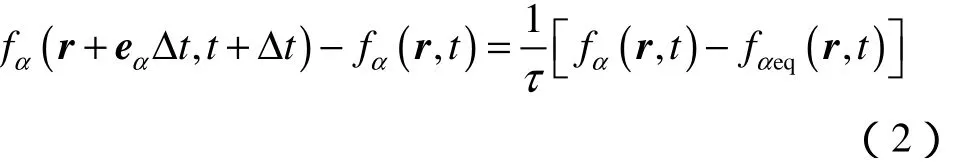
局部平衡态分布函数表示为:


图2 纳米孔道物理模型
模型的速度配置如下:

其中 c x t=Δ Δ
模型的宏观密度、宏观压力和速度定义为:
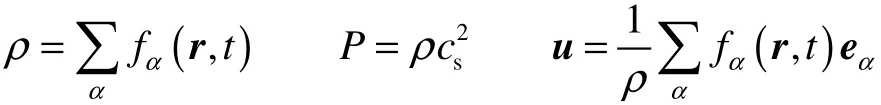
对于微尺度流动,特征参数是 Knudsen数,模型中如何引入 Knudsen数是微尺度流动模拟的关键。基于等温假设,Knudsen数与压力的乘积在沿孔道方向为常数[19-23],即:

本文采用的松弛时间计算公式为:

2.2 边界条件
在格子 Boltzmann模拟中,边界条件起着重要作用。当系统达到稳定之后,流场与初始条件无关,结果主要由边界条件决定。页岩孔隙小、比表面大,气体与有机质孔道表面之间存在吸附解吸行为。Chen等[24]将流体与流体、流体与固体之间的分子作用力引入格子Boltzmann方程,提出了Langmuir边界滑移模型,使得格子 Boltzmann方法可以表征吸附解吸对流动的影响。因此,本文采用此模型进行模拟。此模型基于Langmuir理论,假定气体分子与有机质孔道发生作用时,由于粘合力的影响,首先吸附于孔道壁面之上,一段时间之后从孔道壁面上解吸,吸附与解吸处于动态平衡。壁面处气体速度定义为:

用Fick扩散方程分别求出吸附气和自由气的质量流量为:
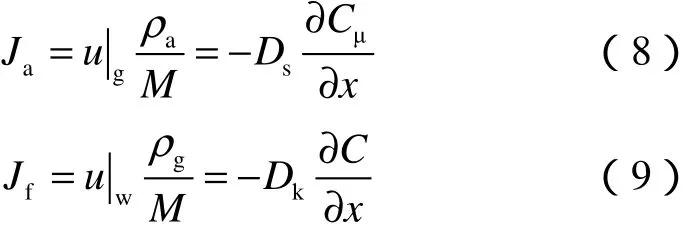
将(8)式、(9)式代入(7)式,求出吸附解吸造成的孔壁速度,即为Langmuir滑移边界条件,表达式为:

为将 Langmuir滑移边界条件应用于格子Boltzmann模拟,需将宏观条件转化为相应的分布函数。定义D2Q9碰撞边界如图2所示,左壁面点O处分布函数f3、f4、f5、f6、f7可通过迁移获得,分布函数f1、f2、f8需要通过 Langmuir滑移模型来确定。依据Chapman-Enskog[15,18]方法,定义壁面处分布函数为:
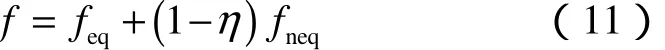
将相应的宏观条件代入,可得O点处的分布函数为[25]:

其中O,B对应图2中的O,B两点。
上下边界采用定压边界,上边界为入口,下边界为出口,孔道中流体在两端压差作用下流动。根据迁移规则,孔道入口段和出口端相应的分布函数如下。
入口端:

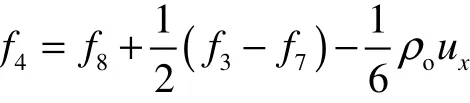
3 模拟结果及讨论
3.1 模型及程序验证
首先与文献的模拟结果进行对比,验证格子Boltzmann方法及程序的正确性。物理模型见图2,基本参数选取如下:x方向网格数Nx=1 100;y方向网格数Ny=11;出口端自由气平均密度为1,本文所有的模型都是建立在等温基础上的。
选取3组模拟参数分别为:出口端Kn数为0.019 4,入口端自由气平均密度为1.4;出口端Kn数为0.194,入口端自由气平均密度为 2;出口端 Kn数为 0.388,入口端自由气平均密度为2。通过格子Boltzmann模拟分别计算出口端速度分布和孔道中心处沿程非线性压力偏差的分布(见图3)。

图3 不同Knudsen数条件下出口端沿程压力非线性分布偏差及出口端速度分布
将计算结果与 MRT-LBE、slip-NS、IP-DSMC和DSMC方法计算结果进行对比。由图3可见,当出口端Kno为0.019 4和0.194时,出口端速度剖面与其他方法计算结果拟合很好(见图 3b、图 3d)。但当出口端Kno为0.388时,笔者的计算结果和其他模型的计算结果均存在偏差(见图3f)。这是因为随着Knudsen数的增大,孔壁附近的 Knudsen层对孔道内的流动逐渐起主导作用。对于孔道中心处压力偏差的分布,笔者计算结果与MRT-LBE方法和slip-NS方法计算结果大致吻合(见图3a、图3c、图3e),但与DSMC和IP-DSMC方法的计算结果差异很大,并且随着 Knudsen数的增大,差异变得越来越大。以上模拟表明:格子Boltzmann方法能较好地模拟出口端流速和沿程压力分布。在滑移区和弱过渡区,LBM模拟结果拟合度很高(见图3a、图3b、图3c、图3d);在高Knudsen数情况下,格子Boltzmann方法需要引进更加复杂的边界处理模型,但在滑移区和弱过渡区,LBM模拟结果有效。气体在页岩有机质孔隙中流动时的Knudsen数为0.006~0.180,属于滑脱流和弱过渡流,因此对于页岩有机质纳米孔道中的气体流动模拟,LBM方法是可行的。
3.2 沿程压力分布
气体在纳米孔道中流动时,存在微尺度效应。同时由于页岩有机质的亲油性,有机质纳米孔表面的气体一直处于吸附、解吸的动态平衡。这些微观渗流因素可能导致页岩有机质纳米孔道中流动与宏观尺度流体流动规律的差异。采用LBM方法模拟气体在有机质纳米孔中的流动行为,并与宏观流体力学的 Poiseuille公式[14]计算结果进行对比。模型计算参数为:孔道长度200;孔道宽度10;出口端压力为1,入口端压力取2,出口端 Knudsen数为 0.1。由图 4可见,传统的Poiseuille流条件下,孔道压力是一条直线,满足线性递减规律。但采用LBM方法模拟得到的页岩纳米孔隙中气体流动压力曲线向上凸出,并且压降主要集中在孔道出口端附近,压力梯度不再是常数,即产生了“压缩效应”[11,26]。压缩效应导致页岩有机质纳米孔中气体流动压力分布复杂,不能再简单地用线性关系表示压力分布,这也说明宏观尺度下的连续介质流体流动规律难以准确描述纳米孔隙中的气体流动行为。

图4 弱过渡流与Poiseuille流压力分布对比
对页岩有机质孔道中压力分布的影响因素进行分析。出口端Kn数为0.08时,不同进出口端压力比条件下沿纳米孔孔道中心处的压力偏差分布见图5。随着压力比的增大,孔道的可压缩性增强,导致压力分布的非线性越来越强。另外,压力分布非线性的最大偏差出现在靠近出口端位置,并且随着压力比的增大向出口端移动。
进出口端压力比为2时,不同Knudsen数条件下孔道中心处沿程压力偏差分布见图 6。随着 Knudsen数增大,气体稀薄效应影响增大,但沿程压力的非线性程度减弱,即气体稀薄效应减弱了压缩效应引起的压力非线性分布。稀薄效应和压缩效应对气体流动起反作用,最终纳米孔道的沿程压力分布由两者综合决定。
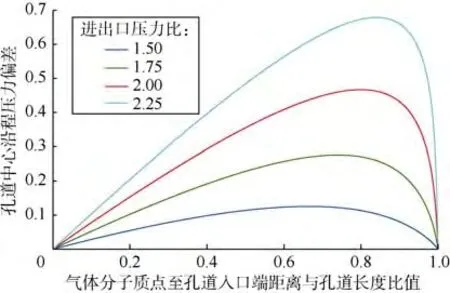
图5 不同进出口压力比条件下沿程孔道中心的压力偏差分布
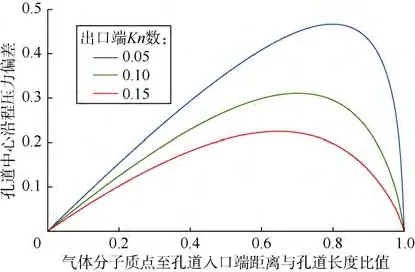
图6 不同Knudsen数条件下孔道中心处压力偏差分布
3.3 边界滑移速度
模型计算格子参数选取如下:孔道长度200;孔道宽度10;出口端压力为1;入口端压力为2;Kno为0.15。图7为LBM方法模拟的气体流动切向和法向速度分布图。由图7a可知,整个流动通道中切向速度剖面与经典流体力学相似,呈现抛物线型。在孔道中心处,沿着孔道长度方向气体流动速度越来越大,并且孔道边界处的切向速度(滑移速度)也越来越大。这是因为,离出口端越近,有机质纳米孔道中压力越低,导致气体密度减小,Knudsen数增大,气体的稀薄效应严重,为了满足质量守恒定律,气体的流动速度必须增大,导致孔道上下壁面发生滑移现象,滑移速度随着孔道压力的减小而增大。

图7 无因次切向、法向速度分布
由经典流体力学理论可知,Poiseuille流在垂直于孔道方向的流动速度为 0[27]。但在纳米孔隙尺度下,垂直于孔道方向的流动速度不仅不为0,而且呈规律变化。图7b表明,纳米孔道中法向速度与常规孔道中法向速度分布差异很大。尽管在上下壁面和孔道中心处,气体的法向速度为 0,但从上壁面或下壁面到孔道中心,垂直于孔道的气体流动速度由 0逐渐增大,并在距离上下壁面1/4处取得极值,然后逐渐减小为0。垂直于孔道的法向速度剖面为中心对称的两个抛物线。沿着孔道方向,随着压力降低,法向速度逐步增大,在出口端达到最大值。法向速度不为 0在一定程度上使得孔道中分子的碰撞更加激励,加剧了分子与分子、分子与壁面的动能交换,促进了气体在页岩有机质孔隙中的流动。
图 8为进出口压力比为 1.5时,出口端 Kn数为0.05、0.10和0.15时的边界滑移速度。由图8可知,Knudsen数对边界滑移速度影响很大,Knudsen数越大,边界滑移速度越大。这是因为,Knudsen数越大,气体稀薄效应越显著,压降梯度越大,在同一位置处的压力越小。压力的减小导致气体分子自由程相应增大。随着分子自由程的增大,分子自由程逐渐逼近甚至超越孔道特征长度,导致气体分子与孔壁碰撞越来越剧烈,在碰撞过程中,壁面处的分子不断地获得动能,所获动能大小随着碰撞程度的增加而增加。因此,Knudsen数的增大导致边界滑移速度增大,滑移现象越来越显著[28]。
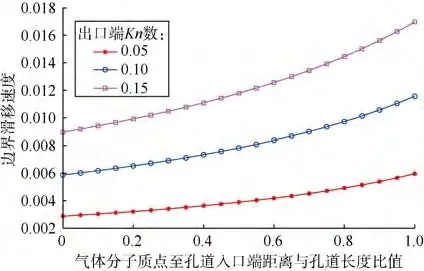
图8 不同Knudsen数下的边界滑移速度
Kno为0.1时,进出口压力比为 1.1、1.2、1.3、1.4、1.5时的边界滑移速度如图9所示。进出口压力比较小时,边界滑移速度较小,此时孔道中压缩效应较弱,压力近似线性分布,所以边界滑移速度也呈线性增加。随着进出口两端压差的增大,惯性作用越来越明显,孔道中气体压缩效应增强。由图 5可知,孔道中压降集中在出口端附近,因此气体速度在出口端附近显著增大,边界滑移速度也显著增大。

图9 不同进出口压力比条件下的边界滑移速度
3.4 质量流量
自由气密度为 1.5、吸附气密度为 1.0、Langmuir压力为1.1时用LBM方法模拟得到的有机质纳米孔中质量流量与孔道两端压差之间的关系如图10所示。在微尺度流动中,质量流量与进出口压力比不再成直线关系,而且滑移速度的出现使质量流量明显增加。由图10可见,当进出口压力比为2.5、Kno=0.01时弱滑移反弹边界的质量流量为2.482,Kno=0.15时反弹边界的质量流量为3.567,随着滑移强度的增大,Kno=0.15时的质量流量是Kno=0.01时质量流量的1.43倍。可见滑移边界是影响质量流量的重要影响因素。这是由于滑脱效应较弱时,气体分子与壁面的动能交换较少,整个流动过程中壁面剪切应力增加较少;随着滑脱效应的增强,切向速度显著增加。

图10 质量流量随两端压差的变化
将反弹边界的模拟结果与考虑吸附解吸的Langmuir边界对比发现,当Knudsen数较小呈弱滑移流时,吸附解吸对质量流量的影响比较小。如Kno=0.01时,Ds/Dk=3.0时的质量流量较Ds/Dk=1.0时的质量流量仅有少量的增加(见图10)。说明当Knudsen数较小时,吸附相的表面迁移对质量流量的影响可以忽略,孔道中气体对流流动占有主导地位。保持孔道两端压差,减小孔径以增大 Knudsen数,结果表明,不论是滑脱效应还是吸附解吸都对质量流量有明显的促进作用。随着吸附解吸效应的增强,质量流量明显增加(见图10)。这是由于,当吸附解吸达到平衡时,固体壁面吸附有一定量的气体分子,吸附分子层具有一定的厚度,导致气体流动特征长度减小,在一定程度上增大了 Knudsen数,增强了流动的稀薄效应,边界滑移速度增大,质量流量随之变大[29-30]。
滑脱效应和吸附解吸效应均对质量流量起重要作用。(7)式中的ug、uw可分别反映滑脱效应和吸附解吸作用对气体流动的影响。定义边界滑移速度与孔道中心气体速度的比值为孔壁无因次速度。由图11可知,当Kno=0.005 6时,壁面速度近似为0,随着吸附解吸强度增大,无因次孔壁速度保持不变,此时吸附解吸作用对气体流动的影响可以忽略不计。当Kno=0.028及Kno=0.056时,随着吸附解吸强度的增大,无因次孔壁速度不断增大,吸附解吸作用对气体流动的促进越来越明显。图11中直线段的斜率和截距分别代表吸附解吸作用和滑脱效应对气体流动的影响。

图11 表面扩散作用对气体流动的影响
4 结论
甲烷气体在页岩有机质纳米孔中流动的 Knudsen数为0.006~0.180,属于滑移区和弱过渡区。采用格子Boltzmann方法可以有效模拟有机质纳米孔道中气体的流动行为。
气体在有机质纳米孔道中流动时存在明显的微尺度效应,在不考虑传热的情况下,主要表现为压缩效应和稀薄效应。压缩效应导致沿纳米孔道的压力呈非线性分布;且孔道两端的压差越大,非线性程度越大。Knudsen数增大,稀薄效应增强,减弱了压缩效应引起的非线性程度。
气体在纳米孔道中流动时边界滑移速度随着两端压差和 Knudsen数的增大而增大,并且在垂直于孔道方向上速度不为零,加剧了孔道中气体分子与边界分子的动能交换,促进了气体在页岩有机质孔隙中的流动。
气体在纳米孔道中的吸附效应和滑移速度对气体的质量流量有重要影响。
符号注释:
Kn——Kundsen数;λ——分子平均自由程,m;kB——格子常数,通常取 1.380 5×10−23J/K;δ——气体分子碰撞直径,m;T——气体的温度,K;p——气体的压力,Pa;fα(r,t)——t时刻 r处速度为 eα的粒子密度分布函数;r——粒子所处的向量空间;t——格子时间;eα——α方向上的粒子速度,无因次;Δt——时间步长,无因次;τ——无因次松弛时间;fαeq(r,t)——α方向对应时刻地点的局部平衡态分布函数;α——离散速度方向,取1~9;ρ,P,u——宏观密度、压力和速度,无因次;ωα——α方向的权系数;cs——格子声速,无因次;Δx——网格步长;po——出口端压力,Pa;Kno——出口端Knudsen数;p(x)——x方向压力,Pa;τ*——修正的无因次松弛时间;υ——格子黏度,无因次;us——壁面处气体速度,m/s;ug——距壁面一个分子自由程处的气体分子速度,m/s;uw——由吸附解吸引起的孔壁速度,m/s;β——壁面吸附分子所占的比例,%;C——自由气浓度,g/m3;Cμ——吸附气浓度,g/m3;Cμs——单分子层最大吸附能力,g/m3;K——平衡分配系数;Ja,Jf——吸附气和自由气的质量流量,g/s;M——气体相对分子质量;x——孔道长度方向;Ds——表面扩散系数;Dk——分子扩散系数;ρa,ρg——吸附气、自由气密度,g/m3;f——任意点的分布函数;feq——平衡态分布函数;fneq——非平衡态分布函数;η——调整系数;ρi,ρo——入口和出口端宏观密度;ux——x方向宏观速度。
[1] 陈新军, 包书景, 侯读杰, 等. 页岩气资源评价方法与关键参数探讨[J]. 石油勘探与开发, 2012, 39(5): 566-571.Chen Xinjun, Bao Shujing, Hou Dujie, et al. Methods and key parameters of shale gas resources evaluation[J]. Petroleum Exploration and Development, 2012, 39(5): 566-571.
[2] 邹才能, 朱如凯, 白斌, 等. 中国油气储层中纳米孔首次发现及其科学价值[J]. 岩石学报, 2011, 27(6): 1857-1864.Zou Caineng, Zhu Rukai, Bai Bin, et al. First discovery of nano-pore throat in oil and gas reservoir in China and its scientific value[J].Acta Petrologica Sinica, 2011, 27(6): 1857-1864.
[3] Sondergeld C H, Ambrose R J, Rai C S, et al. Micro-structural studies of gas shales [R]. SPE 131771, 2010.
[4] 白斌, 朱如凯, 吴松涛, 等. 利用多尺度CT成像表征致密砂岩微观孔喉结构[J]. 石油勘探与开发, 2013, 40(3): 329-333.Bai Bin, Zhu Rukai, Wu Songtao, et al. Multi-scale method of Nano(Micro)-CT study on microscopic pore structure of tight sandstone of Yanchang Formation, Ordos Basin[J]. Petroleum Exploration and Development, 2013, 40(3): 329-333.
[5] Roy S, Raju R, Chuang H F, et al. Modeling gas flow through microchannels and nanopores[J]. Journal of Applied Physics, 2003,93(8): 4870-4879.
[6] Guo Zhaoli, Zhao T S, Shi Yong. Physical symmetry, spatial accuracy,and relaxation time of the lattice Boltzmann equation for microgas flows[J]. Journal of Applied Physics, 2006, 99: 074903-1-074903-8.
[7] Sofonea V, Sekerka R F. Boundary conditions for the upwind finite difference Lattice Boltzmann model: Evidence of slip velocity in micro-channel flow[J]. Journal of Computational Physics, 2005,207(2): 639-629.
[8] Lee T, Lin C L. A characteristic Galerkin method for discrete Boltzmann equation[J]. Journal of Computational Physics, 2001,171(1): 336-356.
[9] Zhang Yonghao, Qin Rongshan, Emerson D R. Lattice Boltzmann simulation of rarefied gas flows in microchannels[J]. Physical Review E, 2005, 71(4): 47702.
[10] Arkilic E B, Schmidt M A, Breuer K S. Gaseous slip flow in long microchannels[J]. Journal of Microelectromechanical System, 1997,6(2): 167-178.
[11] Verhaeghe F, Luo Lishi, Blanpain B. Lattice Boltzmann modeling of microchannel flow in slip flow regime[J]. Journal of Computational Physics, 2009, 228(1): 147-157.
[12] Shan Xiaowen, Yuan Xuefeng, Chen Hudong. Kinetic theory representation of hydrodynamics: A way beyond the Navier-Stokes equation[J]. Journal of Fluid Mechanics, 2006, 550: 413-441.
[13] Bird G A. Monte Carlo simulation of gas flows[J]. Annual Review of Fluid Mechanics, 1978, 10(1): 11-31.
[14] 窦宏恩, 旸杨. 低渗透油藏流体渗流再认识[J]. 石油勘探与开发,2012, 39(5): 633-640.Dou Hongen, Yang Yang. Further understanding on fluid flow through multi-porous media in low permeability reservoirs[J].Petroleum Exploration and Development, 2012, 39(5): 633-640.
[15] Wang F P, Reed R M. Pore networks and fluid flow in gas shales[R].SPE 124253, 2009.
[16] 闫宝珍, 王延斌, 倪小明. 地层条件下基于纳米级孔隙的煤层气扩散特征[J]. 煤炭学报, 2008, 33(6): 658-660.Yan Baozhen, Wang Yanbin, Ni Xiaoming. Coal bed methane diffusion characters based on nano-scaled pores under formation conditions[J]. Journal of China Coal Society, 2008, 33(6): 658-660.
[17] 郭照立, 郑楚光. 格子 Boltzmann方法的原理及应用[M]. 北京:科学出版社, 2009.Guo Zhaoli, Zheng Chuguang. Theory and applications of lattice Boltzmann method[M]. Beijing: Science Press, 2009.
[18] 何雅玲, 王勇, 李庆. 格子 Boltzmann方法的理论及应用[M]. 北京: 科学出版社, 2008.He Yaling, Wang Yong, Li Qing. Lattice Boltzmann method: Theory and applications[M]. Beijing: Science Press, 2008.
[19] Dongari N, Agrawal A, Agrawal A. Analytical solution of gaseous slip flow in long microchannels[J]. International Journal of Heat and Mass Transfer, 2007, 50: 3411-3421.
[20] Lim C Y, Shu C, Niu X D, et al. Application of lattice Boltzmann method to simulate microchannel flows[J]. Physics of Fluids, 2002,14(7): 2299-2308.
[21] Zhang Y H, Qin R S, Sun Y H, et al. Gas flow in micro channels: A lattice Boltzmann method approach[J]. Journal of Statistical Physics,2005, 21(1/2): 257-267.
[22] Tang G H, Tao W Q, He Y L. Lattice Boltzmann method for simulating gas flow in microchannels[J]. International Journal of Modern Physics C, 2004, 15(2): 335-347.
[23] Perumal D A, Krishna V, Sarvesh G, et al. Numerical simulation of Gaseous microflows by lattice Boltzmann method[J]. International Journal of Recent Trends in Engineering, 2009, 1(5): 15-20.
[24] Chen Xinjun, Bao Shujing, Hou Dujie, et al. Methods and key parameters of shale gas resources evaluation[J]. Petroleum Exploration and Development, 2012, 39(5): 566-571.
[25] Fathi E, Akkutlu I Y. Lattice Boltzmann method for simulation of shale gas transport in kerogen [J]. SPEJ, 2013, 18(1): 27-37.
[26] 赵汉中. 微细圆管中气体流动的稀薄效应和可压缩效应[J]. 华中科技大学学报: 自然科学版, 2001, 29(10): 97-98.Zhao Hanzhong. The rarefaction and compressibility effects of the gas flow in circular microtube[J]. Journal of Huazhong University of Science and Technology: Nature Science, 2001, 29(10): 96-98.
[27] 聂德明, 郭晓辉, 林建忠. 微通道中气体流动的格子Boltzmann数值模拟[J]. 计算物理, 2010, 27(3): 390-395.Nie Deming, Guo Xiaohui, Lin Jianzhong. Lattice-Boltzmann method for gas flow in microchannels[J]. Chinese Journal of Computational Physics, 2010, 27(3): 390-395.
[28] 王华龙, 柴振华, 郭照立. 致密多孔介质中气体渗流的格子Boltzmann模拟[J]. 计算物理, 2009, 26(3): 389-395.Wang Hualong, Chai Zhenhua, Guo Zhaoli. Lattice Boltzmann simulation of gas transfusion in compact porous media[J]. Chinese Journal of Computational Physics, 2009, 26(3): 389-395.
[29] 陶然, 权晓波, 徐建中. 微尺度流动研究中的几个问题[J]. 工程热物理学报, 2001, 22(5): 576-577.Tao Ran, Quan Xiaobo, Xu Jianzhong. Several questions in research of micro scale flow[J]. Journal of Engineering Thermophysics, 2001,22(5): 576-577.
[30] 何学秋, 聂百胜. 孔隙气体在煤层中扩散的机理[J]. 中国矿业大学学报, 2001, 30(1): 1-4.He Xueqiu, Nie Baisheng. Diffusion mechanism of porous gases in coal seams[J]. Journal of China University of Mining & Technology,2001, 30(1): 1-4.
