矿井涌水量预测方法及适用性评价

连会青，夏向学，徐 斌，徐 慧,尹尚先

( 1 华北科技学院,北京 东燕郊 101601；2 中国矿业大学(北京), 北京 100083)

0 引言

在煤矿开采过程中，如何准确地预测矿井涌水量，一直是国内外专家都在努力探求的问题。多年来，虽然很多学者从不同角度、利用不同方法做了大量的工作[1]，但到目前为止，涌水量预测数据与井下实测数据存在不同程度的误差，最大可差十几倍，造成矿井涌水量预测误差的原因则很多，概括起来主要有以下三个方面原因：水文地质条件未查清、选用的水文地质参数缺乏代表性、数学模型选择不当[2]。因此，选择恰当的方法预测矿井涌水量是减少误差的重要途径。本文选择新汶矿区为研究对象，对多种矿井涌水量方法的预测结果进行分析，以近10年实测涌水量为对比项，评价了适应该区条件的矿井涌水量预测方法的适用性。

1 矿井涌水量预测方法综述

国内外学者对矿井涌水量的计算预测进行了大量的研究，通过实践总结出了对矿井涌水量预测的各种方法，一类是分布参数法，另一类是集中参数法[3]。其中最典型的有：数值法[4]、解析法[5]、神经网络法[6]、水均衡法[7]和水文地质比拟法[8]。分布参数法用偏微分方程表示，而集中参数法则用常微分方程表示。矿井涌水量预测方法分类见框图1。

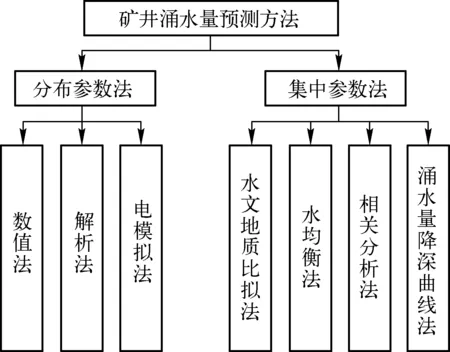
图1 矿井涌水量预测方法分类

1.1 数值法

1.1.1 原理和应用条件

数值法是随着电子计算机的出现而发展起来的一种近似计算方法。从理论上讲它是求解渗流偏微分方程近似解的一种方法，而且该方法在实际应用中可以满足精度要求，解决许多复杂条件下的矿井涌水量问题。数值法对研究区水文地质条件简单、含水层系统简单的情形非常有效。

1.1.2 计算方法

目前常用的地下水资源评价的数值法有：有限单元法和有限差分法两种。

1) 有限单元法：有限元法是把求解的区域划分为有限个不相重叠的单元，在单元上构造出基函数。然后再构造出形状函数，用形状函数作为近似解，最后用伽辽金法或最小势能原理求出结点上的近似值。

2) 有限差分法：有限差分法是把导数近似地用差商来代替，边界条件和初始条件也做类似处理，把定解问题的求解化为一组代数方程组的求解。它的实质就是把描述地下水运动的偏微分方程，近似地用和它对应的差分方程来代替，然后对差分方程来求解。

1.2 解析法

1.2.1 原理和应用条件

解析法是目前矿井涌水量预测中应用最广的一种方法，它适用于任何类型的井巷系统。解析法主要根据解析解的建模要求，运用地下水动力学原理，通过对实际问题的合理概化，构造理想化模式的解析公式，用于矿井涌水量预测。

1.2.2 计算方法

地下水渗流运动的基本定律是达西定律，所有的解析公式都是在此基础上建立或推导出来的。解析法中最常用到的是井流方程，其基本公式分为稳定流公式(裘布依公式)和非稳定流公式(泰斯公式)两大类。

运用解析法时，利用稳定流理论可以解决两方面的问题：在已知开采水平最大水位降深的条件下，预测矿井总涌水量；在给定疏干排水能力的前提下，计算水位降深值。利用非稳定流理论可以解决三方面的问题：已知水位降深和疏干时间，求矿井涌水量；已知水位降深和排水能力，求疏干时间；已知排水能力和疏干时间求水位下降值。

1.3 BT神经网络法

1.3.1 原理和应用条件

人工神经网络(ANN)是应用工程技术、计算机手段模拟生物神经网络的机构和功能的集成，通过大量与自然神经系统细胞相似的人工神经元联结成网络，实现知识并行分布处理的人工智能系统。

1.3.2 计算方法

BP网络结构上分为输入层、隐含层、输出层三层，层与层之间采用全连结方式。输出层可以有多点(神经元)，隐含层可以分为多层。如果隐含层单元数可以自由设计，则用三层S状，可以任意精度逼近任何连续函数。因此通常选用3层网络(隐含层为一层)，既不影响网络的精度，还可以提高网络的速度。

1.4 水均衡法

1.4.1 原理与应用条件

水均衡法是根据水均衡原理，查明矿井开采时水均衡各收入支出部分之间的关系。适用于地下水运动为非渗流型且水均衡条件简单的充水矿床。因此，查明矿区范围内地下水补给、排泄条件，研究矿区在疏干过程中将要产生的变化，合理确定均衡项目和取得各项目数据，方能进行水的均衡计算。

1.4.2 计算方法

它是通过对地下水动态规律的研究，建立矿区在某一期间(均衡期)地下水各收支部分间的变化关系，以建立均衡方程来预测开采地段的涌水量。基本均衡方程为：

Q= (Qc+Qy+Qh+Qyh+Qr)—

(Qc/+Qy/+Qh/+Qzh/+Qr/)—Qch

式中：

Q——开采地段的可能涌水量，m3/d；

Qc，Qc/——地下径流侧向流入量和侧向外泄量，m3/d；

Qy，Qy/ ——越流补给量和越流排泄量，m3/d；

Qh，Qh/——河流补给量和泄往河流的水量，m3/d；

Qyh，Qzh/——大气降水补给量和蒸发消耗量，m3/d；

Qr，Qr/——人工补给量和除本矿井以外的其它人工抽(排)水量，m3/d；

Qch——单位时间内含水层储存量的增长量或消耗量，m3/d。

储存量对承压含水层为弹性量，对潜水含水层为静储量，对于稳定状态，此项为0。

1.5 水文地质比拟法

1.5.1 原理和应用条件

水文地质比拟法以稳定流为基础，利用地质和水文地质条件相似、开采方法基本相同的生产矿井的排水或涌水资料，来预测新建矿井的涌水量。该方法的应用前提是新建矿井与老矿井的条件应基本相似，老矿井要有长期的水量观测资料，以保证涌水量与各影响因素之间的数学表达式的可靠程度，故它只是一种近似的计算方法。

1.5.2 计算方法

水文地质比拟法主要包括富水系数法和单位涌水量法。

1) 富水系数比拟法

就是根据已知矿井富水系数预测邻近的水文地质条件相近、开采方法相同的新矿井矿井涌水量，即：

式中：

Q——新设计矿井涌水量(m3/a)；

Q0——已知老矿井涌水量(m3/a)；

P0——已知老矿井生产能力(t/a)；

P——设计新矿井生产能力(t/a)

2) 单位涌水量比拟法

单位涌水量的物理意义是矿井单位水位降深和单位开采面积的平均实际涌水量。如果矿井涌水量(Q0)随开采面积(A0)和水位降深(s0)而变化，则单位涌水量(q0)为

式中：

q0——生产矿井单位面积上的单位涌水量(m3/h);

Q0——生产矿井总涌水量(m3/d);

F0——生产矿井的巷道采掘面积(m3)

S0——生产矿井的水位降低值(m)；

根据生产矿井单位面积上的单位涌水量，可以计算与其水文地质条件相类似的设计矿井总涌水量：

Qm=q·Fm·Sm

式中：

Fm——设计矿井的设计采掘面积(m2)

Sm——设计矿井的设计年平均水位降低值(m)

2 研究区矿井涌水量预测结果与分析

2.1 研究区概况

研究区以新汶矿区的龙固、济阳和赵官三个井田作为重点研究对象。其中，龙固井田位于山东省菏泽地区巨野县城，区内主采3#煤层，构造程度复杂。济阳煤矿位于黄河北煤田济阳预测区浅部，开采深度：-280m—-750m。赵官煤矿位于德州市齐河县赵官镇，本区的地震烈度为6度，赵官井田可采煤层有4层。

区域内发育主要地层有奥陶系、石炭系、二叠系、侏罗系、白垩系、第三系及第四系地层，其煤系地层分别是石炭系本溪组、太原组和二叠系山西组。矿区内主要含水层有:第四系砂砾岩含水层、第三系砾岩含水层含水层、二叠系山西组砂岩含水层、石炭系太原组石灰岩含水层、石炭系本溪组石灰岩含水层及奥陶系石灰岩含水层。

通过对研究区三个矿井资料的收集及整理，其目的是为了获得水文地质参数，水文地质参数直接影响到预测结果的可信度和准确度。三个矿井资料收集情况如下表1所示。

表1 收集资料情况

2.2 不同方法的矿井涌水量预测分析

在上述资料齐备情况不同的条件下，选择龙固、赵庄、济阳矿，采用数值法、解析法、水文地质比拟法对不同煤层的生产阶段矿井涌水量进行预测，分析各种方法预测结果的误差，以便选择该矿区和类似条件下的矿井涌水量预测最适用方法。

2.2.1 数值法

由于龙固矿井有丰富的资料，及有相对较高的水文地质参数，本次以龙固矿区为例，用数值模拟对矿井涌水量方法进行研究。利用数值模拟求得主要含水层矿井涌水量结果见表2所示。

表2 数值模拟法预测矿井涌水量成果表

有表2可知，数值法的矿井涌水量预测值与实际涌水量相比有一定的变化，但误差较小，说明该模型满足预测精度，可以进行地下水预报。

其中的误差来源有：①计算方法无法完全拟合实际的地下水流运动，这是产生误差的主要原因之一。②水文地质条件认识不足。尽管研究区已经积累了一定的研究成果，但仍缺乏地下水位的长序列观测资料、水文地质参数等资料。

2.2.2 解析法

利用解析法对龙固、赵官、济阳三个矿井进行涌水量预测，其成果见表3。

表3 解析法预测涌水量成果汇总表

由表3可知，涌水量预测值与实际值有一定出入，尤其对于龙固、赵官矿井，解析法预测值误差较大。

其中误差来源：1矿井水文地质条件、边界条件的复杂性以及含水层介质的不均一性都将产生涌水量计算的误差。2选择公式适用范围误差：裘布依方程的适用条件是地下水为稳定流 ,可是解析法计算矿井涌水量时 ,计算水位降深少则数十米 ,大则数百米,井壁水流早已不是缓变流。 3影响半径值的选取误差，矿井影响半径不可能是对称的。

2.2.3 水文地质比拟法

利用水文地质比拟法对赵庄和济阳矿井涌水量预测，其预测成果见表4。

表4 水文地质比拟法预测矿井涌水量成果表

由表4可知，水文地质比拟法预测精度有限，只能用于矿井涌水量的近似计算。比拟条件的确定是预算矿井涌水量的关键。

其中误差来源有：(1)已有矿井涌水量资料与进行预算的勘探区的水文地质条件的差异。(2)确定比拟系数的误差。

3 误差分析和适用性评价

3.1 误差分析

根据矿井涌水量预测的各个环节，将可能引起矿井涌水量预测失真的原因概括为：

1) 对矿床水文地质条件认识不足，矿区水文地质条件未予查清。

2) 水文地质概念模型概化不当。若水文地质参数取值有误或参数分区错误、边界条件概化不当或水流运动形式概化有误都将影响后期计算结果是否准确。

3) 数学模型失真。矿区复杂的水文地质条件和开采系统，通常很难用数学式确切地描述出来，为数学模型建立带来一定困难，稍有不慎就会使数学模型失真。

4) 建井工程及矿区开采过程与地下水数值模拟部分环节有出入。此外，在时间上实际采煤工程是按采区不断采掘的，而在数值模拟处理过程中并未按实际采煤工程分阶段对地下水进行模拟，而是以开采开始时间作为数值模拟起始阶段，整个采煤过程结束点作为模拟末刻，在预测步骤和程序上与实际采煤工程有一定出入。

5) 采煤工艺、建井施工方法及开采速度对涌水量预测的影响。

3.2 矿井涌水量预测方法适用性评价

3.2.1 数值法的适用性评价

优点：①数值法的优点在于它能考虑较多的影响因素，它适应边界条件能力强，善于描述水介质的非均质和各向异性特征，容易处理控制性方程中的源、汇项，圆满的考虑了矿井在大降深疏降过程中所出现的承压转无压的非线性问题；②较好的解决了复杂条件下的各种地下水流状态，且具有较高的精度；③数值法生成的三维地质模型能清楚地反映各个地层的展布信息,任意角度的切面能反映出地层沉积结构信息。

缺点：①建模及运算工作量大、耗时较长，内存和计算量巨大。②需要反复修正涌水量，使各控制点的计算水位下降到设计要求。③对资料的系统性和精确性要求较高。

3.2.2 解析法的适用性评价

优点：①解析法在预测矿井涌水量方面具有简单方便;②适用于任何类型的巷道，以及专门性的疏干排水装置的涌水量计算。

缺点：通过理论分析及实践认为该方法并不适用于大降深不规则矿井的涌水量计算预测。

3.2.3 水文地质比拟法的适用性评价

优点：①水文地质条件比较简单、涌水量不大、水文地质工作程度较低的矿山，或用于同一矿山延深开采或扩大开采时的涌水量预测②在用于已有多年生产历史的矿井时，可根据上一水平的实际排水资料来预测延伸水平的涌水量，或根据生产采区的排水资料预测新扩大采区的涌水量，效果较好。

缺点：①在开采条件下影响矿井充水因素的动态变化没办法考虑周到时，则不能使用该方法进行矿井涌水量预测；②在地质和采矿工程条件不具有相似性的矿井中，则不能使用。

综上所述，解析法运算简便、快速、经济，但由于边界的简化和计算参数的选取影响其预测精度，适用于水文地质条件简单、边界条件简单的矿井涌水量预测；数值法因其计算快适用于解决复杂问题，预测精度高，水文地质比拟法计算方法简单、经济实用，但计算粗糙是一种近似的估计方法，适用于水文地质条件相似的地区且有长期水量观测资料的老矿井；水均衡法计算简单，但均衡要素确定较为困难，适用于求解矿床充水的极限涌水量。

因此，在满足要求和水文地质资料详实的情况下可利用数值法进行涌水量预测。对于研究区资料不够丰富时，可采用数值法进行模拟进行涌水量预测，同时利用解析法进行对比。对于新建的矿井，水文地质参数不足时，可使用水文地质比拟法进行涌水量预测。

4 结论

结合上述原因矿井涌水量预测必须遵循三个基本原则，即：查明条件、选用有代表性的计算参数和选择正确的数学模型。无论用何种方法计算矿井涌水量 一定要进行矿区地下水补给量计算，从水量均衡的角度考虑矿井涌水量计算的合理性。为了顺利取得较好的矿井涌水量计算结果，在勘查设计时，就应该仔细分析矿井水文地质条件，选择合适的矿井涌水量计算预测方法。不同的方法有其特定的使用条件，实际运用中可以采用多个不同的方法。进而通过比较和综合分析，选择确定较为准确的矿井涌水量，这样才能准确且符合实际预测矿井涌水量。建议矿井涌水量计算时，尽量采用数值模拟方法，并辅以其它类比外推方法等。

[1] 杜敏铭,邓英尔,许模. 矿井涌水量预测方法综述[J]. 四川地质学报,2009,29(9701):70-73.

[2] 陈酩知,刘树才,杨国勇. 矿井涌水量预测方法的发展[J]. 工程地球物理学报,2009,(601):68-72.

[3] 宋春辉,杨云龙,郭继锋. 浅析矿井水涌水量预测的几种常见方法[J]. 科技情报开发与经济,2009,19,(22310):177-178.

[4] 马秀媛,李逸凡. 数值方法在矿井涌水量预测中的应用[J]. 山东大学学报(工学版),2011,41，(18905):86-91.

[5] 张帅伟,张清锋,徐志军,张飞. 解析法预测寒武系灰岩含水层涌水量[J]. 科技传播,2012,(6912):157-158.

[6] 吴翠娟. 基于神经网络的矿井涌水量预测研究[J]. 中国煤炭,2009,35，(39910):105-108,113.

[7] 董兴文. 矿井最大涌水量计算和参数确定──试论南方岩溶矿井的水均衡预测方法[J]. 四川地质学报,1995,(01):75-80.

[8] 温文富,曹丽文. 比拟法和解析法在某矿井涌水量预测中的分析比较[J]. 中国煤炭,2011,37(42007):38-40.

[9] 姜素,孙亚军,杨兰,凌成鹏. 基于BP神经网络方法的矿井涌水量预测[J]. 中国煤田地质,2007,(9002):38-40.

[10] 谢道文,施式亮. 基于云理论与加权马尔可夫模型的矿井涌水量预测[J]. 中南大学学报(自然科学版),2012,43(21406):2308-2315.

[11] 骆祖江,杨林,周强. 煤田矿井涌水量预测三维数值模型[J]. 水动力学研究与进展A辑,2010,(2506):737-742.