一种抗扭式模块化联轴器的研究
2014-01-15路伟,毛磊
路 伟,毛 磊
(中船重工第710研究所,湖北 宜昌443003)
联轴器的功能是用于联接两轴或从主动轴向从动轴传递运动的机构。联轴器可起保险作用,防止机构过载损坏设备,或用作自动接通、脱开主从动轴的用途。联轴器的使用已覆盖至各行各业。然而尽管其种类繁多,但在实际应用和选型时还存有诸多不便。因为相同的设备使用条件不同,对器件的性能要求就不同,因而在实际工程上选择联轴器前,通常须经过繁琐的理论计算分析后,才能确定所用联轴器的型号,但从已形成标准系列的联轴器型号来看还是难以满足使用需求的,特别是在新产品开发阶段还应通过试验验证其合理性。为此,作为从事这一行业的工程技术人员就有必要探索、设计制造出一种新型的组合式联轴器,以满足实际工程技术上的需求。
1 设计要求
要求设计出的联轴器工作可靠,在过载情况下能自动断开且不损坏设备,同时具备以下特性:1)结构简单、造价低廉,能承受一定的冲击载荷;2)在装配与工作过程中可补偿两运动轴间的误差。
2 装置组成及功能
一种抗扭式模块化联轴器组装完成后的结构示意见图1,其制造原理是利用金属弹性件自身具有一定的弹性及抗扭转能力来传递能量,因而该联轴器装配于两运动轴或用于主动轴向从动轴传递运动的轴系上时,允许主、从动轴的轴线存有一定的位置偏差,装配要求低,具备活动和弹性联轴器的功能[1];同时采用了承力钢球的连接方式,主轴套与从动轴套之间可相对转动,轴向亦有一定量的变动,且将弹性扭簧包容在轴套内部,起到保护弹性扭簧的作用。
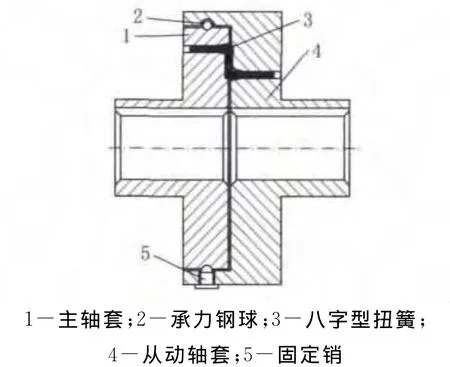
图1 结构组装图

图2 主、从轴套的向视图
3 设计说明
为满足性能要求,在工作过程中确保抗扭联轴器主从动轴正反运转时能均匀受力,且在过载情况下能自动断开而不损坏设备,采用的设计思路是全包容式结构,即将承力构件或易出现断裂的器件安装在封闭的构件内。具体设计方法是:选用高性能弹性金属材料制作承力构件,其结构形式设计成八字型扭簧结构,这样当主动轴由顺时针旋转方向切换至逆时针方向时,起承力作用的八字形扭簧上所承受到的扭力是相同的,仅是受力方向发生变化[2]。需注意的是:如将八字形扭簧设计成一体结构,则图2所示A处所指的孔应设计成腰形孔;如将扭簧设计成单体式,由两件配合组成八字形结构时,图2所示A处所指的孔应设计成两个圆形孔。为提高承力件的使用寿命,预防构件在装配或使用时损伤,在主、从轴套上装配八字形扭簧的端面位置上,分别开有呈八字形的腰形槽,两构件对接后形成的槽深之尺寸不大于扭簧所用钢丝的截面直径,其他尺寸与扭簧相应,结构形式见图1、图2。为降低装配时的工艺要求,将轴套上安装扭簧的孔设计成喇叭口状,且为圆弧过渡。这样设计的目的一是较小承力扭簧在装配过程中不受外界作用力的影响[2];二是减小锐边对扭簧的作用力;三是将承力扭簧安装在主从轴套内,形成全封闭结构,可防止扭簧断裂后飞出伤人。为保证主从轴套间的连接强度及装配时的精度要求,在主轴套与从动轴套相配合的大径外圆上加工有半圆形沟槽,同样在从动轴套相对应的内环上也设有半圆形的沟槽,两轴套对接后形成的环状圆形沟槽尺寸必须与承力钢球的外形尺寸相配,这样既可将主从轴套牢固地连接在一起,又确保了主从轴套间有一定的位置活动量,补偿装配时带来的不大装配误差,同时亦可补偿轴线有一定的偏移量的误差[3]。为便于承力钢球的安装,在从动轴套上的半圆形沟槽正上方开有螺纹通孔,其尺寸略大于承力钢球的直径,这样可将钢球顺利装入由主从轴套形成的环形槽内,然后用固定销封装,以确保工作时承力钢球不会从环形槽内滑出。
由于该弹性联轴器具有上述的结构特点,所以可依据实际使用工况的要求,组合成结构相同而性能指标不同的弹性联轴器,其实施方法是用模块化的设计方法,即选用不同材质的金属制作成不同刚度和强度的八字形弹性扭簧,或选用性能指标相同但配以不同数量扭簧组成不同性能指标的联轴器。为保证装配完成后的联轴器具有在一定范围内的位移活动量,除上述方法外还需说明的一点是将固定销的头部设计成半球头形,其尺寸与承力钢球的直径相同,装配到位后,应与主轴套的半圆形沟槽底部有一定量的间隙,以达到其运动时的灵活性要求[3]。
4 结束语
该抗扭式模块化联轴器具有结构简单、造价低廉,且能承受一定的冲击载荷作用,确保被保护的设备不受损坏,同是还具备以下特点:
1)利用弹性扭簧自身的弹性和恢复力,结合结构上的特点,使其具有一定的浮动性能,在工作过程中可补偿两运动轴不大的装配误差;
2)采用了承力钢球的连接方式,使两轴套之间可相对转动,且在轴向亦有一定量的变动,同时将弹性扭簧包容在轴套内部;
3)选取不同弹性模量的材料,制成外形尺寸相同,刚度不同的扭簧即可组成不同的联轴器,拓宽了该构件的适用范围。
[1] 成大先.机械设计手册(第1卷)[M].第四版.北京:化学工业出版社,2002.
[2] 杨荣柏.机械优化设计[M].北京:机械工业出版,1988.
[3] 贝伊尔R.机构运动学综合[M].陈兆雄译.北京:机械工业出版社出版,1987.
