二维周期阻尼薄板结构的声辐射特性

朱 帅，吴星成，杨 瑶，田 丰

（湖北汽车结构振动与噪声控制工程技术研究中心，湖北 武汉430068）

薄板结构作为工业生产中最常见结构之一，其振动辐射的噪声在环境噪声中占极大的比例。Park J和Mongeau L等人将板的边界支撑等效为弹簧和扭簧的组合来分别表征弹性力和弯矩作用，研究了不同边界条件对板结构声辐射的影响［1］。Liu B L等人对附带加筋板的弯曲航空板结构的传声损失进行了理论和实验研究，发现环向肋板对结构传声损失的影响较小，而轴向肋板对其影响很大［2］。国内学者黎胜等人也对薄板结构声辐射的研究做出了大量的贡献［3－5］。对周期阻尼薄板结构声辐射的研究目前仍相对较少，且大多集中在结构振动带隙方面［6－7］，针对二维乃至多维周期阻尼薄板结构声辐射特性，特别是结构材料对其声辐射特性影响的研究仍然是空白。本文通过改变二维周期阻尼薄板结构的晶格常数和密度，利用有限元和边界元结构的方法研究参数的改变对此类结构声辐射特性的影响，为粘弹性阻尼材料在实际工程结构中的设计和分析提供思路。

1 理论建模

在有限元法中，结构位移响应

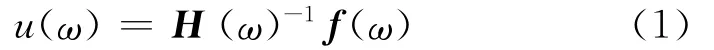
式中：H（ω）＝ （K＋jωC－ω2M），K、C、M 分别为结构的刚度矩阵、阻尼矩阵和质量矩阵；f（ω）为外部激励载荷向量。

在边界元法中，对位移响应求导可得结构速度响应。由于声学响应计算中要求速度响应为法向速度，所以须对每个速度矢量乘以一个指向结构外部的法向矢量n，由此得到结构法向速度响应

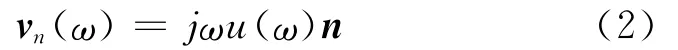
将式（2）带入Neumann边界条件中有

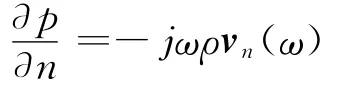
联合Helmholz微分方程及无穷远处的Sommerfeld辐射条件可得Helmboltz积分方程

式中：r为结构表面到声场中任意一点的距离；x、xa分别为声场中和结构上任意一点；G（r）＝为自由空间格林函数，k为波数；O、S、I分别表示结构边界元模型外部、表面及内部。

将边界元模型两侧带入式中，再将两方程相减，求得边界元两侧的单层势：

声压梯度声压差

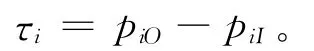
式中，piO与piI分别为边界元模型外侧和内侧声压。

利用有限元离散化的思想，便可得到声场中任意点的声压表达

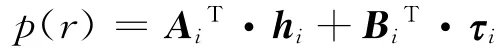
式中Ai、Bi分别为向量系数［8］。

2 仿真模型的建立

仿真整体流程如图1所示。

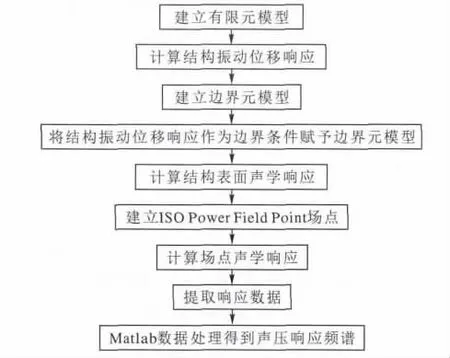
图1 仿真流程图

其中结构有限元模型中薄板选用shell63单元，阻尼选用solid45单元，网格划分满足最小分析波长含6个以上单元的条件，阻尼和薄板结合处用GLUE命令进行粘接并对节点进行压缩处理。另外，薄板采用四点简支，在其一端的中点处施加幅值为5N的点谐激励，分析频率为0～1000Hz。其有限元模型基本结构和材料参数见表1和表2，有限元与边界元模型见图2和图3。

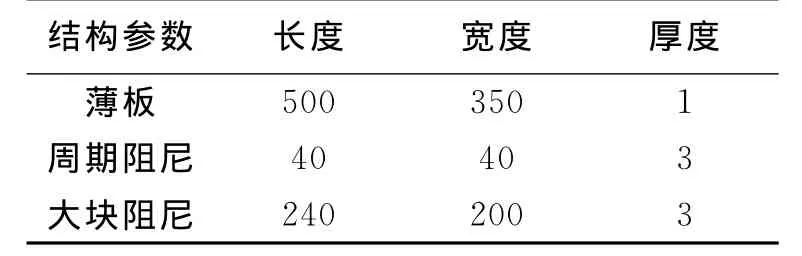
表1 基板及阻尼尺寸 mm

表2 材料基本参数

图2 二维周期阻尼薄板结构有限元模型

图3 二维周期阻尼薄板结构边界元模型

3 数据RMS处理

ISO Power Field Point Mesh场点网格由38个场点构成，场点将结构模型全方位包络，提取38个场点上的声压值并对其进行RMS处理，能较为全面反映结构的声辐射特性。另外对一段频率的声压幅频数据取其均方值，能反映该段频率上结构的声辐射特性。ISO Power Field Point Mesh场点网格见图4。

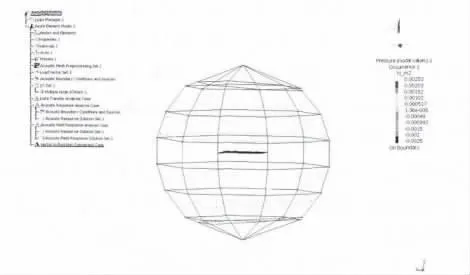
图4 ISO Power Field Point Mesh场点网格

数据RMS处理表达式如下：

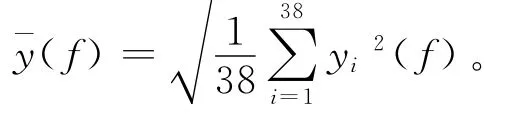
式中：i为场点编号；yi（f）为第i个场点在频率f处的有效声压值；y－（f）为所有场点在频率f处的声压均方值，且

其中，y（f）为声压均方幅频曲线在频率f处的有效声压值，fmin、fmax分别为频率段的起止频率，y－为声压均方幅频曲线在频率段fmin到fmax上的声压均方值。

4 计算结果分析

将二维周期阻尼结构与传统大块阻尼结构和光板进行声学响应对比，在得到二维周期阻尼结构性能优势的基础上对影响此结构声学性能的两个参数（晶格常数和密度）进行单一变量法分析。

4.1 两种阻尼结构与光板声辐射特性对比

大块阻尼结构与二维周期阻尼结构如图5、6所示。

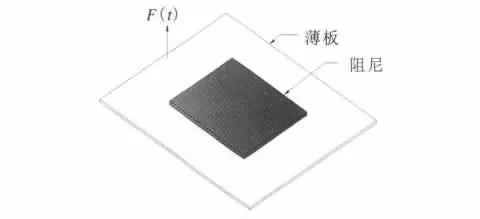
图5 大块阻尼薄板结构示意图

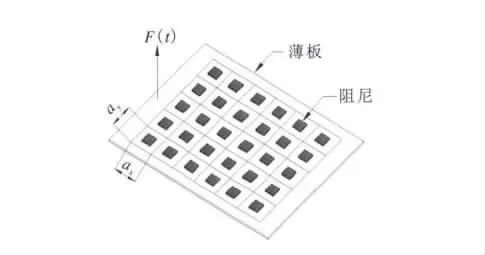
图6 二维周期阻尼薄板结构示意图

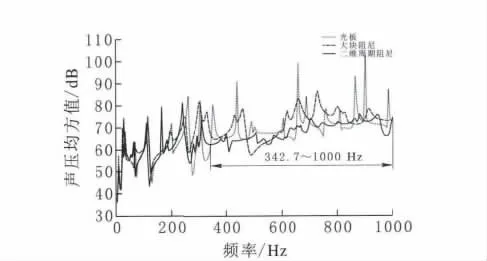
图7 三种结构辐射声压对比曲线

由图7可见，二维周期阻尼薄板结构的声辐射曲线整体峰值较小，在342.7Hz以后明显平缓。对0～1000Hz频段三条声压曲线进行RMS处理，光板、大块阻尼和二维周期阻尼的声压均方值分别为82.20dB、75.99dB和73.10dB，可见二维周期阻尼薄板结构低频段的声辐射特性明显优于传统大块阻尼结构。

4.2 晶格常数对二维周期阻尼结构声辐射特性的影响

二维周期结构其晶格常数有两个方向，设结构长度方向为X方向，宽度方向为Y方向。研究时，取一方向晶格常数保持为均布状态，对另一方向晶格常数进行变量分析，分析结果见图8。如图8所示，在X方向，0～500Hz频段内随着该方向晶格常数的增大，辐射声压逐渐减小，0～1 000Hz频段内也大致如此。在Y方向，0～500Hz频段内随着晶格常数的增大，结构辐射声压减小，而在500～1 000 Hz频段规律仍有待进一步研究分析。但值得注意的是，改变X方向的晶格常数对结构声辐射特性的控制效果更加明显。

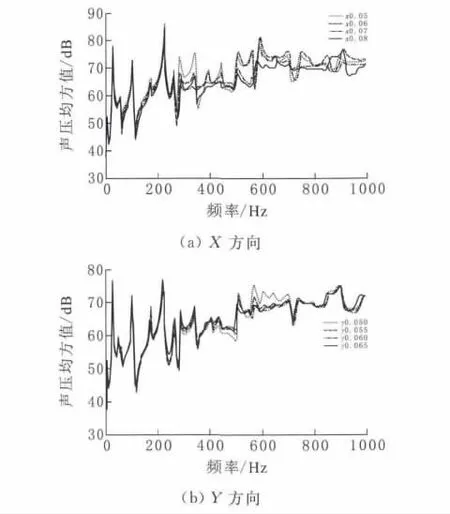
图8 不同晶格常数下辐射声压曲线

分别对各情况下0～500Hz和0～1 000频段辐射声压曲线进行RMS处理，得到结果见表3和表4.

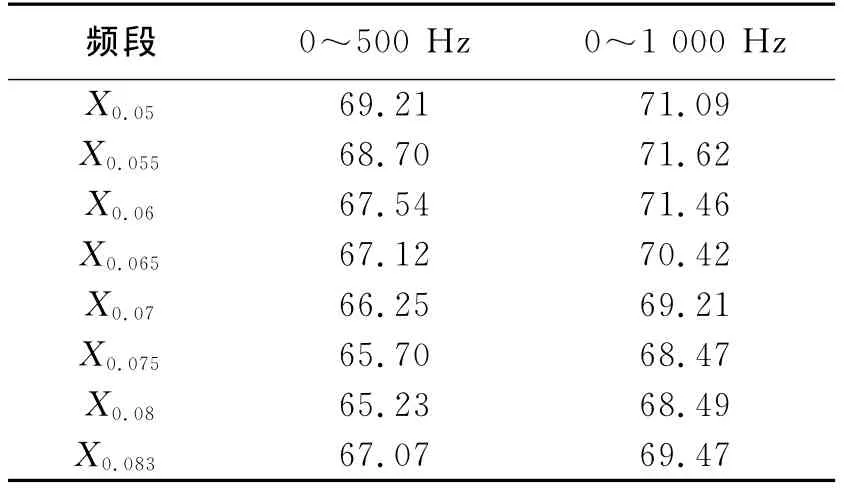
表3 不同X方向晶格常数的辐射声压均方值dB

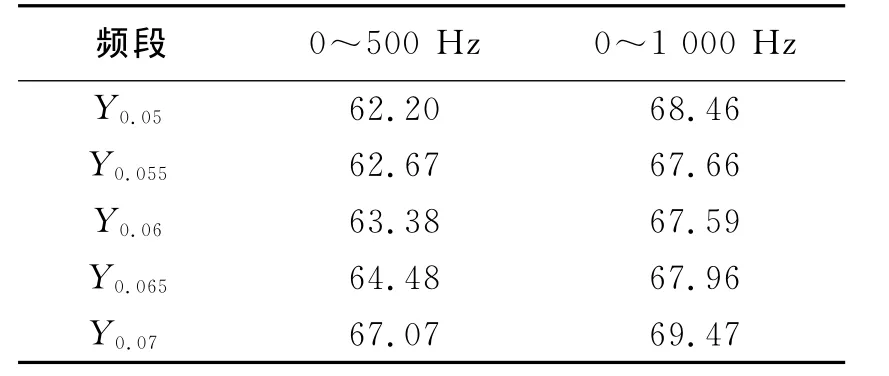
表4 不同Y方向晶格常数的辐射声压均方值dB

由表3、4可知，晶格常数并不是越大结构辐射声压越低。就单一方向而言，在0～500Hz，结构辐射声压在X方向晶格常数为0.08m时达到最低，Y方向晶格为0.05m时最低；0～1 000Hz频段内X方向晶格常数为0.075m时结构辐射声压达到最低，Y方向晶格常数为0.06m时最低。此时若继续增大晶格常数，结构辐射声压反而增大。

考虑实际工况，对X、Y方向不同晶格常数进行组合分析，取效果较好的18组进行对比分析，其结果见表5。

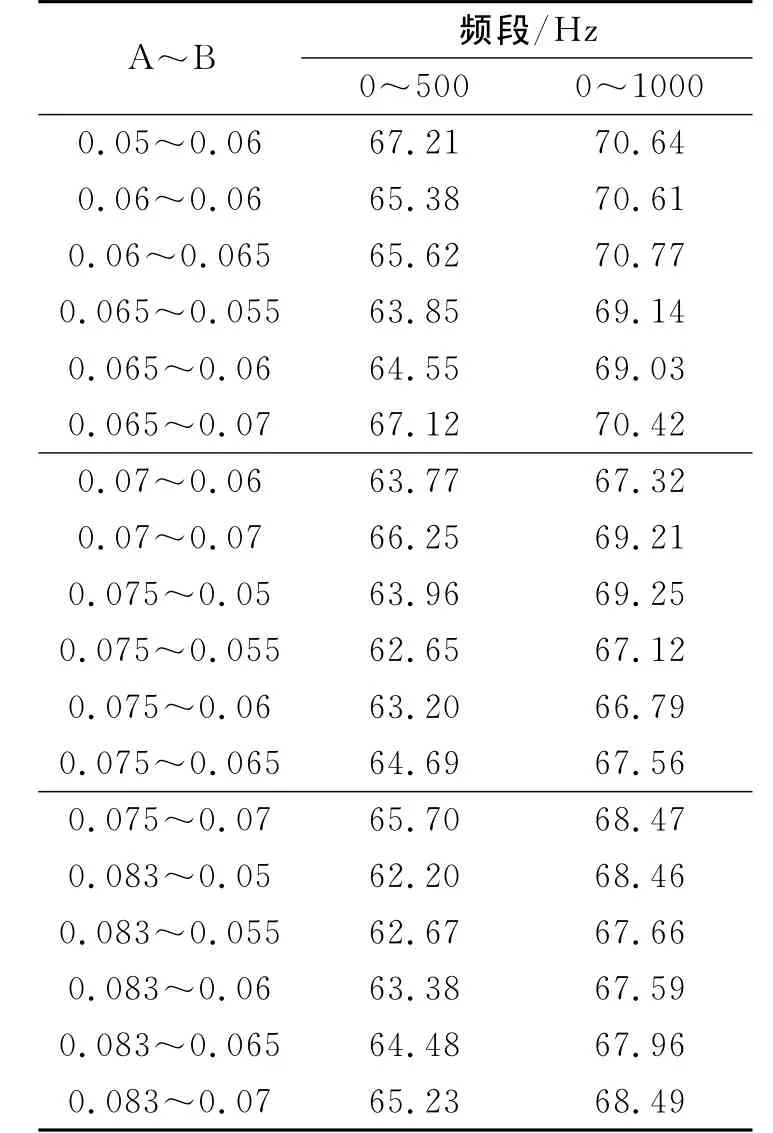
表5 不同晶格常数辐射声压对比 dB

由表5可知，0～500Hz频段内，X、Y 方向晶格常数分别为0.083m与0.05m时结构辐射声压最小，0～1 000Hz频段，X、Y方向晶格常数分别为0.075m与0.06m时结构辐射声压最小。其他频段最优解可采用同样方法求得。

4.3 密度对二维周期阻尼结构声辐射特性的影响

由图9和图10可见，无论是薄板还是阻尼材料，随着密度的增大，场点声压均方值逐渐降低，且峰值向低频方向移动，这主要是由于结构质量矩阵增大的原因，这和结构模态分析得到的模态频率结果相一致，且改变薄板密度的效果更加明显。

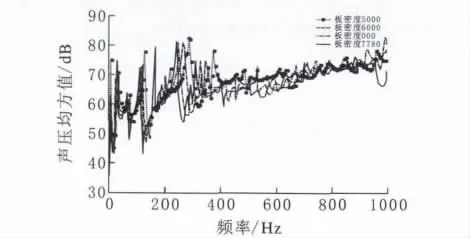
图9 不同薄板密度下辐射声压

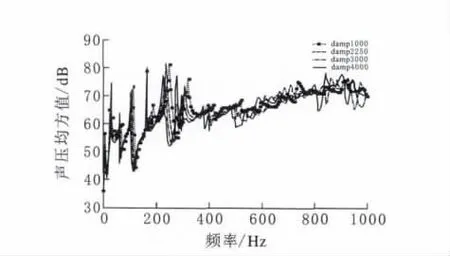
图10 不同阻尼密度下辐射声压曲线

5 结论

1）二维周期阻尼薄板结构低频段的声辐射特性明显优于传统大块阻尼结构；

2）改变该类结构X方向的晶格常数对结构声辐射特性的控制效果相对Y方向晶格常数更加显著，且在0～500Hz，X、Y 方向晶格常数分别为0.083m与0.05m 时最优，0～1 000Hz频段，X、Y方向晶格常数分别为0.075m与0.06m时最优；

3）一定范围内，增大薄板和阻尼密度能降低结构的声辐射，使峰值向低频方向移动，且前者效果更加明显。

［1］ Park J，Mongeau L，Siegmund T.Influence of support properties on the sound radiated from the vibrations of rectangular plates［J］.Journal of sound and vibration，2003，264（04）：775－794.

［2］ Liu B L，Feng L P，Nilsson A.Sound transmission through curved aircraft panels with stringer and ring frame attachments［J］.Journal of sound and vibration，2007，302（4－5）：760－776.

［3］ 黎 胜，赵德友.用耦合有限元／边界元方法研究加筋板的声传输［J］振动工程学报，2001，14（03）：364－367.

［4］ 黎 胜，赵德友.加筋板结构声传输研究［J］.船舶力学，2001，5（04）：61－66.

［5］ 毛崎波，姜 哲.简支矩形板声辐射的有源控制［J］.声学技术，2002，21（03）：118－121.

［6］ 王 刚，温激鸿，韩小云，等.二维声子晶体带隙计算中的时域有限差分法［J］.物理学报，2003，52（08）：1 943－1 947.

［7］ 郁殿龙，刘耀宗，王 刚，等.二维声子晶体薄板振动特性［J］.机械工程学报，2006，42（02）：150－154.

［8］ 李增刚，詹福良.Virtual.lab Acoustics声学仿真计算高级应用实例［M］.北京：国防工业出版社，2010：21－22.