超短波接收机预选滤波器的设计与实现

黎 琴，常雨芳，梅 冬，李 斌，方 勇，唐 静

（1常州国光数据通信有限公司，江苏 常州213000；2湖北工业大学电气与电子工程学院，湖北 武汉430068；3武汉理工大学信息工程学院，湖北 武汉430070）

现代无线通信设备不断增加，信号更加拥挤，电磁环境日益复杂。传统的超短波接收机前端电路已适应不了现代电子干扰、对抗、侦察与反侦察等技术的发展。而扩频通信所具有的强抗噪声、抗干扰、抗衰落、抗多径能力，对接收机前端电路的抗邻道干扰性能及其综合指标提出了更为严格的要求［1－3］。

本文重点讨论位于超短波接收机射频前端输入的选频电路，通过对高选择性能的选频滤波电路的分析，研究低插损、低带内波动、高信号选择及超强抗邻道干扰性能的前端预选滤波器，解决超短波接收机难以克服的邻道超强干扰问题，从而改善接收机的性能［4－5］。

1 超短波抗干扰预选滤波器设计方案与性能分析

1.1 抗干扰数控预选滤波器的设计方案

本文提出的超短波抗干扰数控预选滤波器结构如图1虚框所示。由天线接收并经过前端保护电路的超短波无线电信号输入到分波段数控电调谐滤波器1，进行跟踪选频，并消除邻带干扰和噪声，得到的信号经过增益控制放大器放大，再由数控电调谐滤波器2进一步滤除带外干扰，最后输出给超短波接收机混频器［6］。

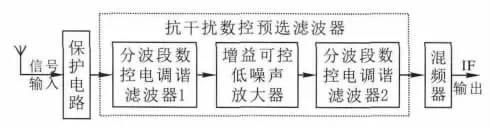
图1 超短波抗干扰数控预选滤波器简化结构图

1.2 抗干扰预选滤波器的特性分析

抗干扰预选滤波器的关键是输入端选频回路的设计与实现，其对系统性能影响最大。本设计采用电感耦合型双调谐回路（图2）。与常用的互感耦合、电容耦合相比，电感耦合减少了回路的相互影响，使调节更加方便［7－8］。

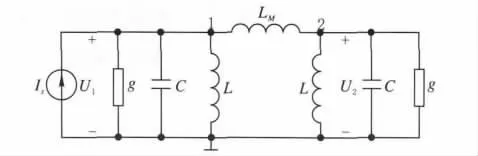
图2 电感耦合双调谐回路

1.2.1 电感耦合双调谐回路特性 图2中若只考虑初级接信号源对选频回路影响，将次级短路，即＝0（图3a），则

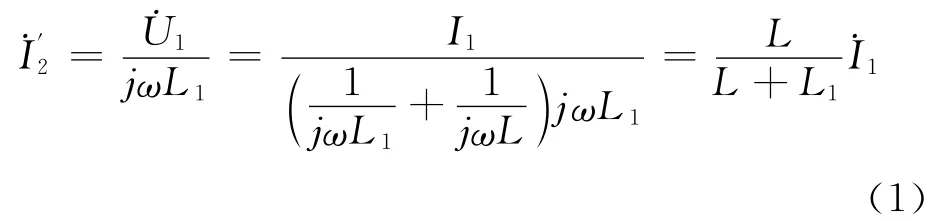
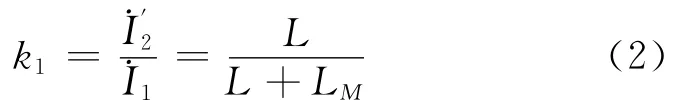
若只考虑回路Π对回路Ι的影响时，如图3b所示，由回路对称性，易得电流与的比值为

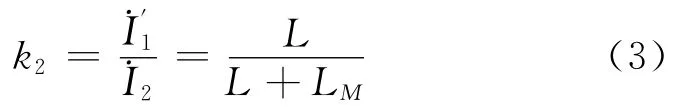
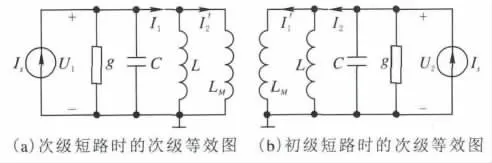
图3 电感耦合双调谐回路的初、次级等效图

故电感耦合双调谐回路的耦合系数

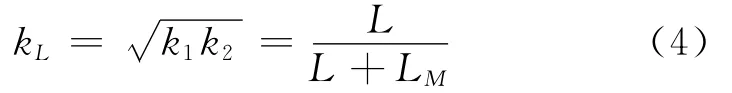
再由回路节点电流法得图2中节点1、2的节点方程如下：

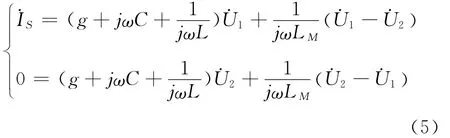
可解得输出电压

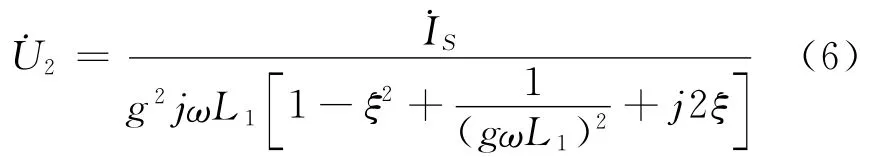
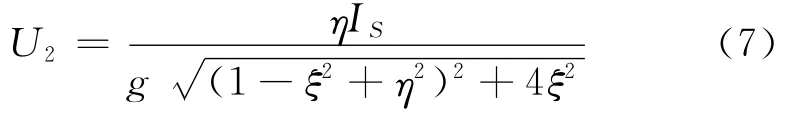
当式（7）中η＝1时，在ξ＝0处，电压U2的极大值为U2max＝Is／2g，与（7）式相比可得谐振曲线的相对抑制比

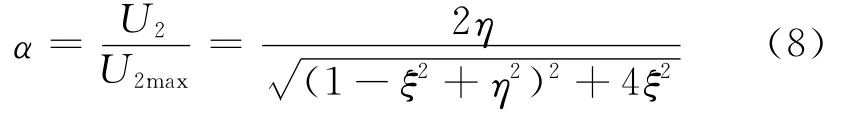
通常称最佳全谐振时初、次级间的耦合为临界耦合，此时初、次级回路满足谐振条件及阻抗匹配条件，当Q1＝Q2＝Q时有临界耦合系数kLc≈1／Q，故高Q电路其临界耦合系数很小。

1.2.2 两级级联双调谐回路特性 由图1可知输入信号经第一级双调谐回路和放大器后，将再通过一级结构相同的双调谐回路进一步选频。由式（8）知一级双谐振回路临界耦合时的谐振曲线为2／，而总谐振曲线应为两级双调谐回路谐振曲线的乘积，即A（ω）／A（ω0）＝4／（4＋ξ4），分别令4／（4＋ξ4）＝1／和4／（4＋ξ4）＝0.1，可得两级双调谐回路级联后的矩形系数

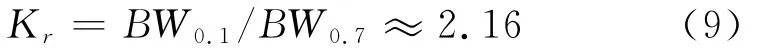
可见，电感耦合双调谐回路通过两级级联后，矩形系数比单级双调谐回路更为理想，大大提高了选频放大器的选择性能。

2 超短波抗干扰预选滤波器的设计

调谐回路的最高谐振频率与最低谐振频率之比称为频率覆盖系数，用Kf表示，即

超短波波段为30～88MHz，综合考虑其应具有高选择性、低带内波动等要求，将其划分为两个波段，可算出Kf≈1.71，降低了频率覆盖系数，容易保证良好的电调谐特性。分段后频率范围分别为30～51MHz和51～88MHz。由此设计的分波段超短波电调谐预选滤波器及其控制电路框图见图4。由反相器与开关 K11、K12、K21、K22控制波段选择；经过低噪声放大器进行增益可控的信号放大；而由电感耦合双调谐回路组成的两级分段电调谐滤波器分别位于放大器电路的输入、输出端，对放大处理前后的信号进行跟踪滤波。

以第二波段51～88MHz为例，对电调谐滤波器进行设计。滤波器电路采用图2所示电感耦合的双调谐回路，在L、C调谐回路中，电容可变化的最大容量与最小容量之比为电容覆盖系数KC，由式（10）及ω2＝1／（LC），则有：

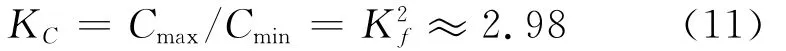
若选取电感L值为330nH，回路的谐振频率分别为该波段频率边界值51MHz和88MHz时，带入f＝1／（2π）可得电容C值分别约为29.5pF和9.9pF，其电调谐性能可由变容二极管来实现。图5为选用的变容二极管BB148的电容值随反向电压变化的特性曲线，当反向电压从－1V～－10 V变化时，电容的变化范围约为40pF～8pF，其电容覆盖系数5＞2.98，满足要求。再综合考虑影响回路Q值的诸因素，取回路最佳全谐振时Q值约为20，将L＝330nH代入可得耦合电感LM＝6.27μH 。

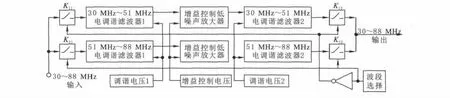
图4 超短波数控抗干扰跟踪预选滤波器组成框图

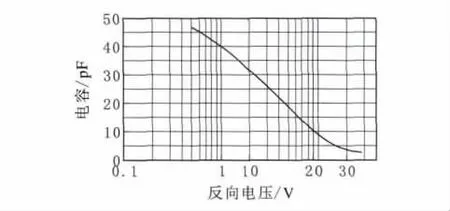
图5 变容二极管BB148的电容值随反向电压变化的特性曲线

图6 为设计的超短波抗干扰预选滤波器第二波段的电原理图。为避免接收信号过强使变容二极管导通对回路影响，将两支变容管同极性背靠背联接再两组并联，如图6中D11～D22，则其总容量仍相当于单管电容值。同时并联2～7pF半可调电容C11～C22方便于微调容值。前、后两级谐振回路的输入、输出均通过抽头耦合，与系统要求的50Ω阻抗良好匹配。

调谐电压一和调谐电压二分别压控两级双调谐回路中的变容二极管的电容值，实现电调谐第二波段51～88MHz频率范围的双调谐回路跟踪选频滤波与干扰抑制，两级间插入增益控制低噪声放大器放大。其中，低噪声放大器选用噪声系数小，其输出1dB压缩点和三阶互调截点高，输入、输出电阻均为50Ω的宽带MMIC放大器芯片，保证放大器的良好线性度。

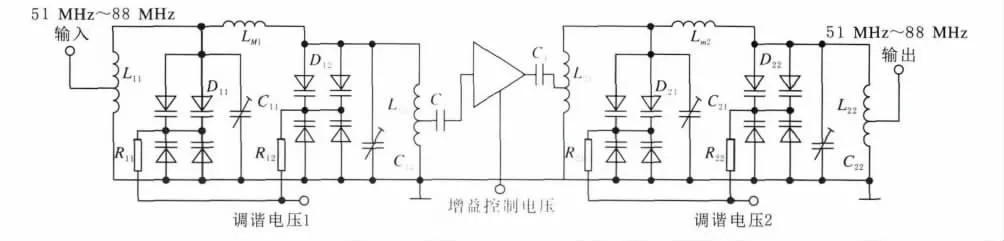
图6 第二波段数控抗干扰预选滤波器电原理图

第一波段（30～51MHz）的设计中电路结构完全相同，电感L值取为820nH，则耦合电感LM为15.58μH，电容值调节范围为34.3～11.9pF。

3 仿真及指标测量

采用Agilent公司的ADS软件分别对所设计的超短波抗干扰预选滤波器的笫一波段和笫二波段进行仿真［9，10］。笫一波段的中心频率为40.4MHz时的仿真结果见图7，可看出，当频率为36.4MHz（低于中心频率约10%）时，衰减约为34.4dB；当频率为44.4MHz（高于中心频率约10%）时，衰减约为35.8dB。笫二波段的中心频率为60.9MHz时的仿真结果见图8，可看出，当频率为54.8MHz（低于中心频率约10%）时，衰减约为35.9dB；当频率为67MHz（高于中心频率约10%）时，衰减约为38.1dB。可见，本文所讨论的电感耦合双谐振滤波器电路具有较高的选择性及抗邻道干扰能力，可以满足超短波数控抗干扰跟踪预选滤波器的指标要求。

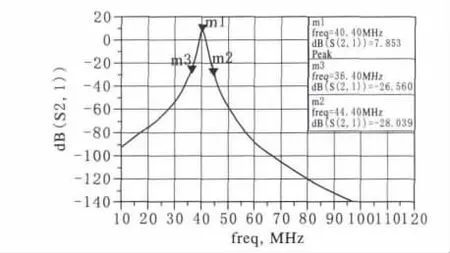
图7 中心频率为40.4MHz时的仿真结果

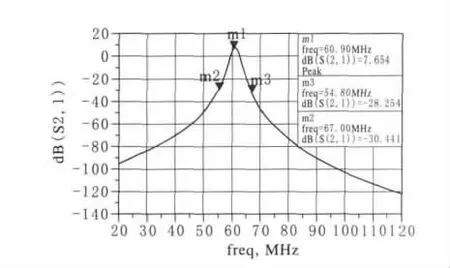
图8 中心频率为60.9MHz时的仿真结果

对实际设计的超短波抗干扰预选滤波器电路的笫一波段和笫二波段分别选三个频率点，采用Agilent公司的S参数网络分析仪，测试在中心频率点的增益值及偏离调谐频率±10%频率处的衰减值如表1所示。

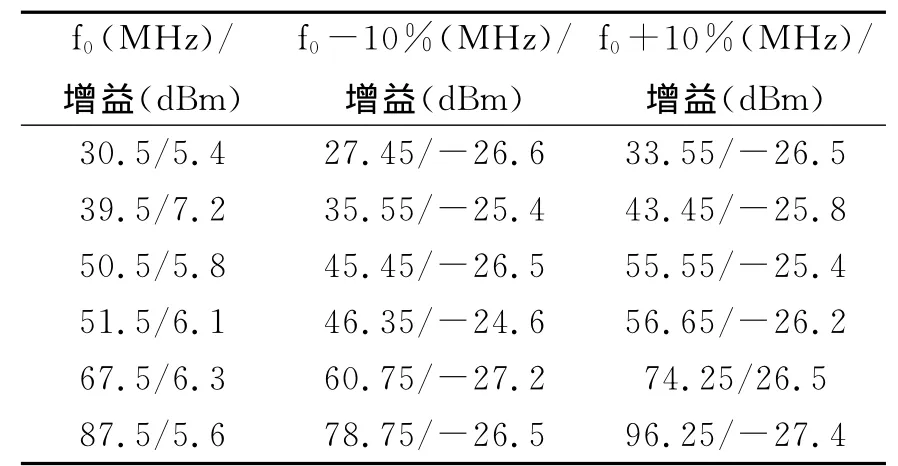
表1 室温条件下频率为f0、f0＋／－10%时的增益值

从表1可以看出，取一波段的中心频率为50.5 MHz时，f0处的增益为5.8dBm，f0＋10%频率为55.55MHz时测得增益为－25.4dBm，衰减值为31.2dBm；而f0－10%时频率为45.45MHz处的增益为－26.5dBm，衰减值为32.3dBm。在二波段中心频率为87.5MHz处的增益为5.6dBm，而f0＋10%频率为96.25MHz时增益为－27.4 dBm，衰减值为33dB；f0－10%频率为78.75 MHz处增益为－26.5dBm，衰减值为32.1dB。可见，实测数据与仿真结果相差不大，验证了所设计的预选滤波器具有较好的抗住了邻道干扰性能。

4 结论

由电感耦合双调谐回路构成的超短波抗干扰预选滤波器，通过改变调谐电压控制变容二极管参数实现预选跟踪滤波，对实际制作滤波器样品的测试数据初步达到了所要求的性能指标，具有工作频率切换速度快、调谐精度高、体积小等特点。目前已经实际应用于实验室超短波接收机射频前端电路中。下一步的优化设计目标是提高其选择性、降低带内插损。

［1］ Joshi H，Sigmarsson H H，Moon S，et al.High－Q fully reconfigurable tunable band－pass filters［J］.IEEE transactions on microwave theory and techniques，2009，57（12）：3 525－3 533.

［2］ 尤志刚.基于变容二极管的跳频滤波器研究与实现［D］.电子科技大学图书馆，2013.

［3］ Metelev S A.Modification of the Watterson model of the ionospheric HF radio communication channel for adaptive spaced reception［J］.Radiophysics and Quantum Electronics，2012：1－12.

［4］ Mirzaei A，Darabi H.A Low－Power Process－Scalable Super－Heterodyne Receiver with Integrated High－Q［J］.Solid－State Circuits，IEEE Journal of，2011，46（12）：2 920－2 932.

［5］ 常铁原，韩 娜，陈文军，等.一种可变耦合数控跳频滤波器电路设计［J］.电测与仪表，2014（02）：72－75.

［6］ Djoumessi E E，Tatu S O，Wu K.Frequency－agile dual－band direct conversion receiver for cognitive radio systems［J］. Microwave Theory and Techniques，IEEE Transactions on，2010，58（01）：87－94.

［7］ 陈永泰，刘 泉.通信电子线路原理与应用［M］.北京：高等教育出版社，2011.

［8］ 尤志刚，林先其，邓立科等.电调谐滤波器的研究与设计［J］.通信技术，2011，44（01）：162－163，167.

［9］ 王燕君.一种基于ADS的电调谐滤波器的新设计［J］.电讯技术，2012，52（03）：367－370.

［10］陈 锟，代 兵，朱正平，等.一种分段无源预选滤波器的设计［J］.中南民族大学学报：自然科学版，2012，31（01）：75－79.