基于遗传算法的入侵检测系统特征选择方法研究

郭 慧，王晓菊，刘明艳，余生晨

(华北科技学院 计算机学院，北京 东燕郊 101601)

0 引言

入侵检测是一种通过收集和分析待检测数据来发现入侵行为的技术。入侵检测系统中，收集到的待检测数据用特征来描述，分类器根据所提取的特征来判断当前行为是否属于入侵行为，而这些特征中却往往包含大量不相关和冗余信息，使用于分类的特征数量过多，增加计算的复杂程度，使分类器的性能变差，系统检测效率下降。因此，如何在保证入侵检测系统具有较高检测率的前提下，通过恰当的方法进行特征选择，去除不相关特征和冗余特征，减少特征数量，选取出最优特征组合，从而提高检测效率，已经成为当前研究的热点问题[1]。很多研究者对此展开了研究，例如，郑洪英等人提出使用粒子群优化算法对特征进行选择[2]；文献[3]采用Relief算法基于统计相关性来选择特征；杜卓明等人使用遗传算法与支持向量机相结合[4]等等。

本文提出一种基于遗传算法的特征选择方法，采用遗传算法搜索特征空间，依据Fisher准则[5]计算特征的适应度函数，根据计算结果对每种特征组合的分类能力进行评价，根据评价结果进行特征的选择、交叉和变异，最终选取出最优特征组合。

1 基于遗传算法的特征选择

特征选择也称特征子集选择，是指从全部特征中选取一个特征子集，使构造出来的模型更好。特征选择能剔除不相关和冗余的特征，选取出最优特征组合，减少特征个数，简化模型，提高系统效率。寻找最优特征组合就是一个搜索整个特征空间的过程，搜索策略包括完全搜索、启发式搜索、随机算法等[6]。

本文采用遗传算法搜索特征空间。遗传算法属于随机算法中的一种，源于达尔文进化论，根据适者生存、优胜劣汰等自然进化规则进行搜索计算和问题求解。基于遗传算法的特征选择是把整个特征空间映射为遗传空间，把每个特征作为一个基因，每一种特征组合称为一个基因链码，即染色体，所有染色体组成群体。根据预定的适应度函数计算群体中每个染色体的适应度，适应度值越高则说明该染色体越优良。根据适应度计算结果以及预先设定的选择算子、交叉算子和变异算子对各染色体进行选择、交叉和变异，得到下一代群体。然后进行反复迭代，直到满足停止条件为止，从而得到最终选取的特征组合。

许多研究者针对基于遗传算法的特征选择方法也进行了深入的研究，如，朱红萍等人通过删除冗余和不相关特征以及偏F检验优化特征子集，再运用遗传算法得到最优特征组合[7]；赵新星等人提出了结合粗糙集与基于聚类的遗传算法的特征选择法来优化入侵检测系统[8]等等。本文将Fisher准则应用于遗传算法中适应度函数的设计，提出了一种快速高效的特征选择方法。

2 特征选择过程

基于遗传算法的特征选择的具体过程包括产生初始群体、计算适应度、选择、交叉、变异、判断终止条件等步骤，通过各步骤的多次反复迭代最终选取出最优的特征组合，如图1所示。

2.1 产生初始群体

在特征选择中，一个特征是否被选中是一个二值问题，因此采用二进制一维编码，数字1表示该特征被选中，数字0表示未被选中。假设特征总数为n，用一个n位的0和1构成的链码表示n维特征空间的一种特征组合，每种特征组合作为一个染色体。随机产生L个特征组合作为初始种群G(t)。

2.2 计算适应度

适应度是用于评价特征组合分类效果的准则，反映了特征组合对分类的贡献[9]。根据适应度函数中是否包含分类器，将其分为过滤器模式和封装器模式[10]。本文研究的是过滤器模式的适应度函数，过滤器通过分析特征组合的内部特点来衡量其好坏，与分类器的选择无关。常用的过滤器模式适应度函数包括相关性度量，距离度量，信息增益，支持向量机，神经网络等[10]。

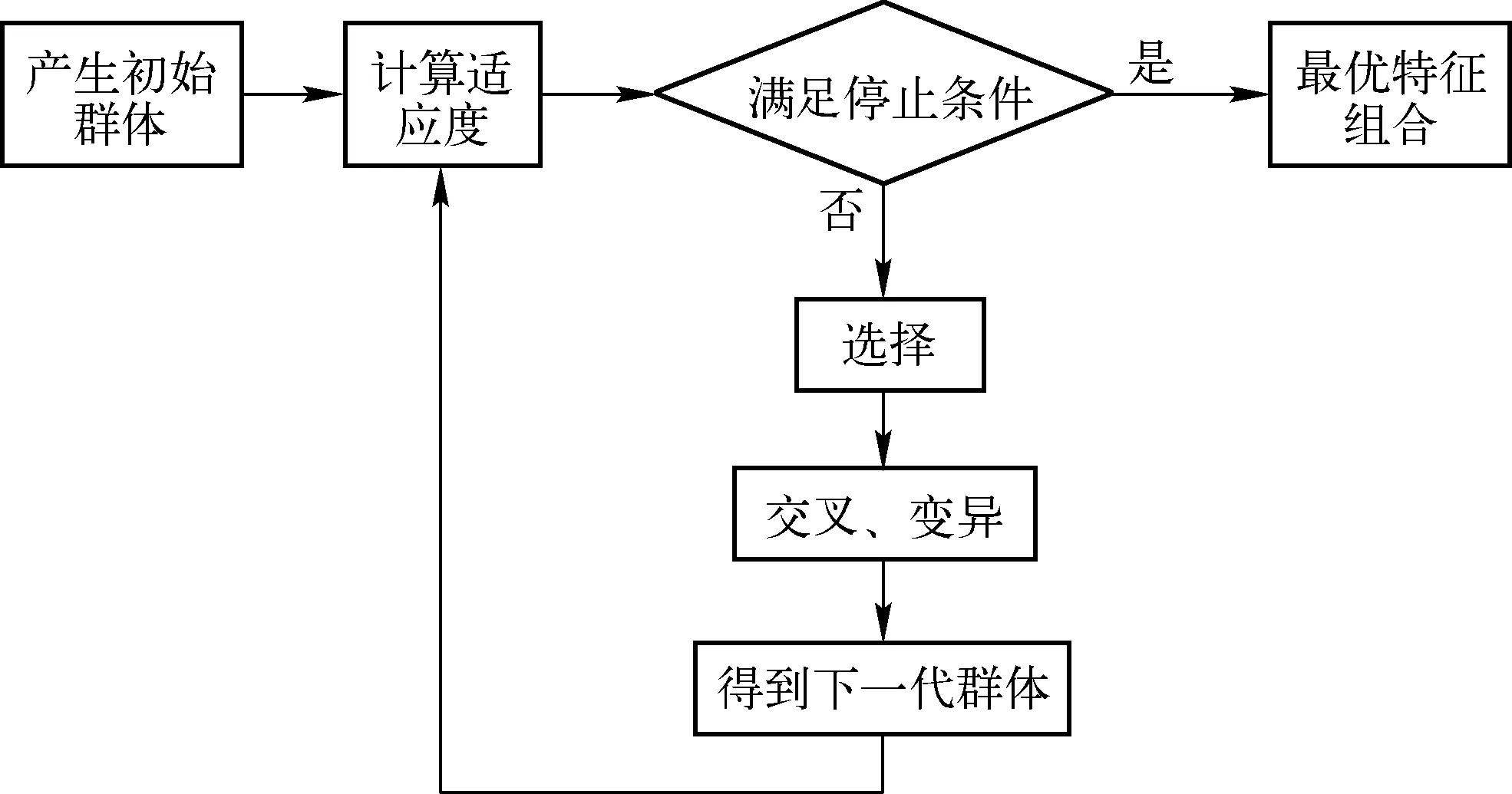
图1 最优特征组合选择过程

在入侵检测系统中，把各种正常的用户行为分为一类，而把各种入侵行为分成另一类。一个好的样本分析的结果是各类类内样本的相似程度越大越好，而各类类间的样本相似程度越小越好。Fisher准则是特征选择的有效方法之一，其主要思想是分类能力强的特征能够使类内样本的差别尽可能小，类间样本的差别尽可能大。本文依据Fisher准则设计特征组合的适应度函数，设Sw表示样本的类内离散度，用于表示同一类中样本的差别，Sb表示样本的类间平均离散度，表示各类之间样本差别的均值，特征组合的Sb值越大Sw值越小则说明该特征组合具有越优越的分类能力。因此，根据Fisher准则，使用Sb与Sw的比值作为特征组合的适应度函数。

假设入侵检测系统共有n个特征x1，x2，x3…xn，m个数据样本y1，y2，y3…ym，样本yi在各特征上的取值组成一个向量yi=(yi1，yi2，yi3…yin)T。有如下定义：

定义1 各类样本的均值向量。设样本共分为c个类别，分别为T1，T2…Tc，Ni是Ti类中的样本数量，mi为Ti类样本的均值向量，则mi的值为Ti类样本的各特征值之和与Ti类中样本数量的比值，即

定义2 所有样本的均值向量。将各类样本的均值向量与先验概率的乘积求和，得到所有样本的均值向量M。Pi是Ti类的先验概率Pi=Ni/m，m为样本总数，Ni为Ti类样本数量，即

定义3 距离平方和。样本yi和yj的距离平方和dij为两个样本各特征值的差的平方和，即

i=1,2…m，j=1,2…m

定义4 样本的类内离散度。把Ti类中各样本与Ti类的均值向量的距离平方和的均值定义为Ti类的类内离散度Swi。即

i=1,2…c，yj∈Ti

定义5 样本的类间平均离散度。把各类别样本的均值向量与所有样本的均值向量的距离平方和的均值作为类间的平均离散度Sb，即

定义6 适应度函数Je定义为：类间的平均离散度与各类类内离散度之和的平均值之比。即

其中，Swi是Ti类的类内离散度，Pi是Ti类的先验概率。

将初始群体中的各特征组合带入上面的公式中，计算出其适应度函数Je的值。Je值越大，说明各类间样本的相似程度低，各类内样本的相似程度高，即类间离散度大，类内离散度小，即说明该特征组合的分类效果越好。

2.3 选择

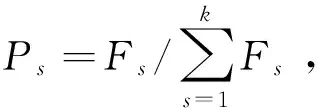
2.4 交叉和变异

将选择算法挑选出的各特征组合对进行交叉。采用单点交叉的方式，对于每对特征组合，随机选取一个基因位，将两个特征组合在此位置上的基因码按照交叉概率Pc(0.5<=Pc<=0.9)进行交叉互换。

将交叉后得到的特征组合进行变异，采用基本位变异算子，随机选择若干个特征组合，在被选中的特征组合中随机选取一个基因位，按照变异概率Pm(0.005<=Pm<=0.01)对该位置的基因码进行取反运算，得到变异结果。

2.5 终止条件

在经过选择，交叉和变异后，得到下一代群体G(t+1)，然后进行反复迭代，直到满足终止条件。通常情况下，当适应度函数达到某个阈值，或达到一定的迭代次数，或所有个体中高位出现一致的比率达到预先设定的阈值，或满足其他停止条件时，停止搜索。设Pt为高位出现一致的个体所占比例的阈值，T为最大遗传代数，当这两者中的其中一个满足时算法终止。选择含1个数最少的特征组合作为最优解，则该特征组合中编码为1的基因位所对应的特征即为被选择的特征。

3 仿真实验

实验数据来源于KDD CUP 99[11]，该数据库与真实环境相似性很大，广泛用于对入侵检测系统日志数据进行分析研究。在实验中，首先使用本文提出的算法在全部41个特征中选取出最优特征组合，然后采用基于反向传播神经元网络作为分类器建立入侵检测系统并对系统的性能进行评价。

3.1 实验数据和设置

本文采用KDD CUP 99中的corrected数据集作为实验数据集，该数据集共有41个分类特征，所有数据被划分为“正常”和“异常”两类。实验首先在corrected数据集中随机抽取50000条数据用于进行特征选择，另外再随机抽取50000条数据用于建立入侵检测系统和进行性能评价。

实验采用的输入参数设置为：初始种群规模为100，交叉概率Pc范围为0.5～0.9，变异概率Pm范围为0.005～0.01，高位出现一致的个体所占比例的阈值Pt为80%，最大遗传代数T为300。

3.2 特征选择结果

采用本文方法进行特征选择，在所有41个特征中选取出了9个，结果如表1所示。

表1 特征选择结果

3.3 入侵检测系统性能评价

实验建立的入侵检测系统为一个三层的反向神经元网络，分别由9个输入层节点，5个隐含层节点和1个输出层节点组成，输出向量值为0代表正常用户，1代表异常用户。将本文算法选取出的9个特征作为神经元网络的输入，在corrected数据集中随机抽取50000条数据，其中50%的数据作为训练集对神经网络进行训练，其余50%作为测试数据。

实验使用了四种特征组合进行训练和测试，分别为原始特征全集、文本算法选取出的特征组合、参考文献[7]和参考文献[8]选取出的特征组合，主要在入侵检测系统的检测时间、检测率和误报率三个方面进行了比较，实验结果如表2所示。

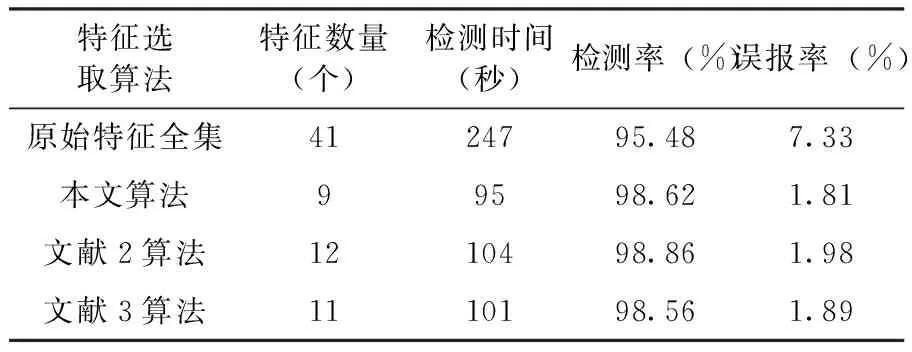
表2 不同特征选择算法比较结果

从实验结果可以看出，使用本文算法选取出的特征组合进行入侵检测与使用特征全集相比，检测时间缩短了一半，同时检测率提高，误报率下降。与文献[7]、[8]相比，采用本文方法选取出的特征数量最少，因此检测时间最短，系统的效率最高，而同时，系统的检测率并没有明显的降低，误报率也没有明显升高。因此，使用本文选取出的最优特征组合对网络行为进行识别，可以在保持较高检测率和较低误报率的同时提高整个系统的检测效率。

4 结束语

本文提出了一种基于遗传算法的入侵检测系统最优特征组合选择方法，使用遗传算法对特征空间进行搜索，依据Fisher准则设计适应度函数，通过计算适应度函数的值来判断每种特征组合的分类能力，然后进行选择、交叉和变异得到下一代特征子集，通过反复迭代得到最优特征组合，去除了不相关特征、冗余特征以及分类能力较低的特征。最后通过实验证明了该方法可以简化入侵检测系统的计算过程，提高系统效率，同时又保证了较高的检测率和较低的误报率。

[1] LEE W K. Feature Selection of Intrusion Data Using a Hybrid Genetic Algorithm Approach[J]. Wireless Networks，2007，13(6)：459-460.

[2] 郑洪英，侯梅菊，王渝.入侵检测中的快速特征选择方法[J].计算机工程，2010，36(6)：262-264.

[3] 蒋玉娇，王晓丹，王文军,等.一种基于PCA和Relief的特征选择方法[J].计算机工程与应用，2010，46(26)：170-172.

[4] 杜卓明，冯静.改进遗传算法和支持向量机的特征选择算法[J].计算机工程与应用，2009，45(29)： 28-31.

[5] 王飒，郑链.基于Fisher准则和特征聚类的特征选择[J].计算机应用，2007，27(11)：2812-2813.

[6] 姚旭，王晓丹，张玉玺,等.特征选择方法综述[J].控制与决策，2012，27(2)：161-165.

[7] 朱红萍，巩青歌，雷战波.基于遗传算法的入侵检测特征选择[J].计算机应用研究，2012，29(4)：1217-1219.

[8] 赵新星，姜青山，陈路莹等.一种面向网络入侵检测的特征选择方法[J].计算机研究与发展，2009(46)：477-482.

[9] 王树，杜启军，余桂贤等.网络入侵检测系统的最优特征选择方法[J].计算机工程，2010，36(15)：140-144.

[10] 陈友，程学旗，李洋,等.基于特征选择的轻量级入侵检测系统[J].软件学报，2007，18(7)：1639-1651.

[11] KDD CUP 1999数据集[DB/MT]. http://kdd.its.uei.edu/databases/kddcup99/task.htm，1999.