基于AR模型参数的导航系统故障检测
2014-01-15丁东方
金 天,丁东方,丛 丽
(北京航空航天大学 电子信息工程学院,北京 100191)
随着导航技术的发展,系统的可靠性成为普遍关注的研究热点,为了保证系统的可靠性,必须对系统进行实时的故障检测和隔离(FDI)。70年代开始,很多学者对FDI进行了研究,其中应用较为广泛的是基于模型的FDI方法[1-4],该方法通过设置一定的观测器来检测系统是否存在故障,比较有代表意义的是3δ检验和残差χ2检验,然而两种算法对一些大的突变故障具有良好的检测效果,但对一些小于10δ的小幅值突变故障检测效果不是太理想[5-6]。为此,鉴于两种检测存在的问题,文中提出了一种利用AR模型参数变化来进行故障诊断的算法,其模型简单,计算量小,工程中也便于实现,同时它不仅对大的突变故障具有良好的检测效果,对一些小于10δ的小幅值突变故障也有较好的检测效果。
1 AR模型参数估计原理
对于时间序列{Xt}t=1,2,…N,AR(n)模型的表达式为
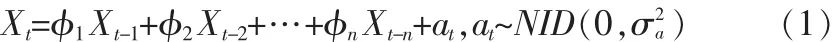
参数估计方法就是按照一定的方法估计出 φ1,φ2,…φn,这n个参数,其中n为AR模型的阶数。at为均值为0,方差为σ2a的白噪声。AR模型参数估计一般采用最小二乘算法进行精估计[7-8]。
由于GPS伪距新息数据是连续的时间序列,可以进行AR建模,当其连续的时间序列中某些数据发生故障时,将改变系统的动态特性从而影响伪距新息序列的特性,使得其不再具有白噪声特性,均值不再为零,另外其方差阵也将偏离滤波理论值,从而导致AR模型参数发生变化,因此可以利用AR模型参数的变化进行这类系统的故障检测,即这类系统的故障检测问题就转化为如何尽可能快地检测AR模型参数的改变。
2 基于AR模型参数变化的导航系统故障检测模型
基于AR模型参数变化的导航系统故障检测模型如图2所示。

图1 仿真系统模型框图Fig.1 The simulation diagram of the system model
其基本思路为:确定AR模型阶数为n,时间序列个数为m,可得到 n个参数分别为 φ1,φ2,…φn,。 利用 N 组 GPS 正常工作时输出的新息序列来训练AR模型,则可得到N组φ1,φ2,…φn。由于N组参数相互独立则可通过求出其标准差δ和μ均值,将其整理成标准正态分布,因此可以用卡方分布检验法来进行故障判别。根据奈曼-皮尔逊准则,由给定的虚警概率 Pf,就可由 χ2分布求出门限值 TD,然后利用公式:λk=φk-μ2,k=1,…,n 是否大于 TD进行判断,当 λ(k)>TD时,系统故障发生,当λ(k)≤TD时,系统工作正常。
3 仿真分析验证
为了验证算法性能,利用软件构建了整个仿真系统,着重比较其在实际应用中的故障检测效果。
3.1 AR模型参数变化
设定AR模型阶数为5,每组时间序列个数为60,选取100组GPS伪距新息时间序列利用MATLAB进行仿真,并分别在每组新息数据最后2个、10个、30个数中加入5δ(δ=6 m,为伪距噪声的标准差)的故障,进行仿真验证,这里我们分别比较5个参数的变化。
仿真结果分别如图2~图6所示。
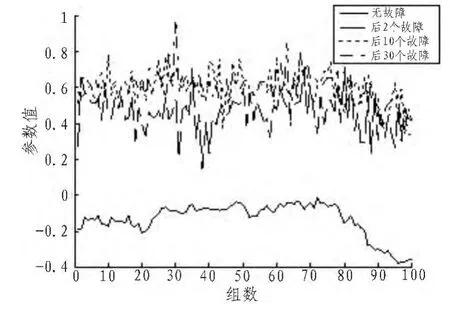
图2 参数1变化Fig.2 Parameter 1 change
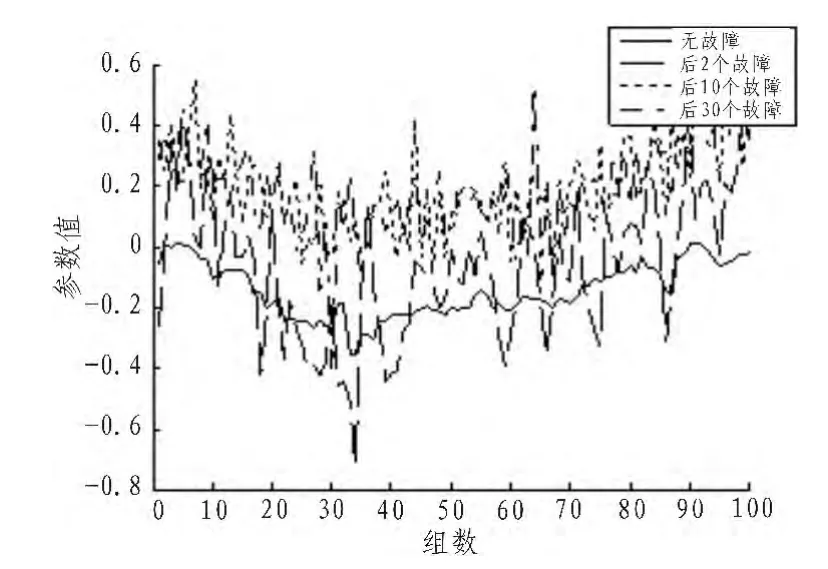
图3 参数2变化Fig.3 Parameter 2 change
从图2中可以看出当每组GPS新息加入故障时,参数1都有明显的突变,而其余参数变化不大,因此可以利用参数1的变化来进行故障检测,而且当每组新息数据只有后2个有故障时,其参数1就会有明显的突变,可以看出其对故障相当敏感。
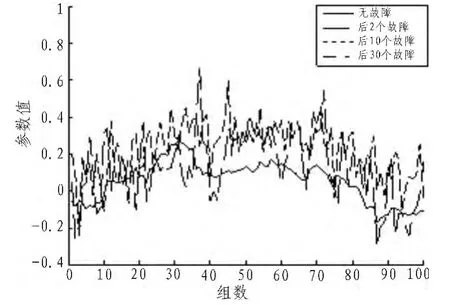
图4 参数3变化Fig.4 Parameter 3 change

图5 参数4变化Fig.5 Parameter 4 change

图6 参数5变化Fig.6 Parameter 5 change
3.2 基于AR模型参数变化的导航系统故障检测模型仿真
首先选取900组GPS正常输出的新息序列 (阶数为5,时间序列个数为60)来训练AR模型,可以获得900个φ值,从而可以得到其均值u为-0.309 4,标准差δ为0.153 6,设其虚警概率为10-4,自由度为1,则可求出其门限T0为15.136 7。
本文构建的仿真系统利用了GPS/INS组合导航系统中一颗卫星输出的1 000 s GPS伪距新息数据进行仿真验证,并从第61 s开始加入不同幅度的故障。其基本思路为:先利用前60 s数据求出参数1,然后剔除第一个新息加入第61 s输出的新息数据计算一个新的参数1,以此类推,可以实时得到参数1,实时得到的参数1都代入公式求出此刻的 λ1。
仿真结果分析:由图7中可以看出当在61秒加故障时,在62秒时已经可以检测出故障,但当故障延续57秒后它的参数会恢复正常,这时已经检测不到故障。为了避免这种情况,我们需要对其进行改进来确保数据的实时检测和持续报警。
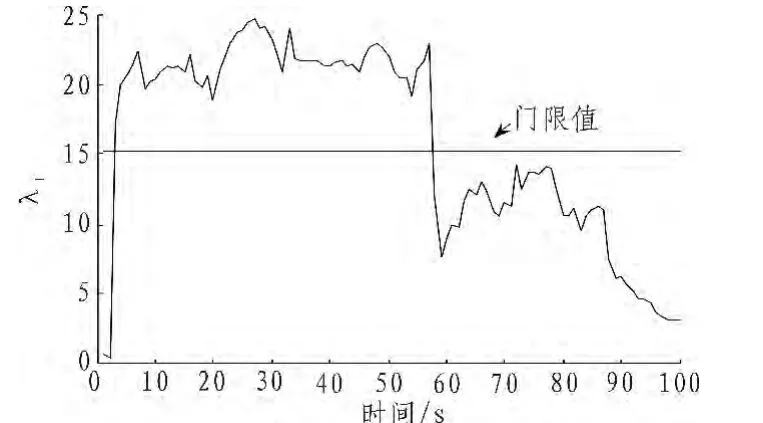
图7 故障检测仿真示意图Fig.7 The fault detection simulation diagram
4 带重置的AR模型参数故障检测算法
新的设计实现原理为首先预存59个新息数据,其中58个为GPS正常工作时的新息数据,第59个数据为故障数据,当GPS传感器开始工作时将其实时新息数据送入AR模型中进行实时计算,此时时间序列个数为60,可以得到其参数,并通过公式进行判断。如果连续出现十次故障,则将其数据剔除,返回并再次启用原来预存的新息数据进行实时计算,这样如果GPS新息出现故障时,它可以实现连续报警,如果GPS新息恢复正常,它可以正常工作。其仿真结果如图8所示。
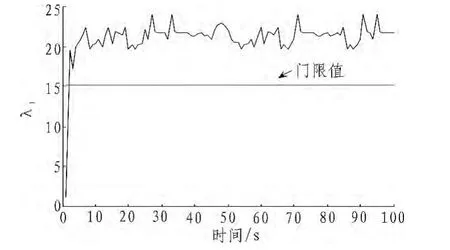
图8 带重置的AR模型参数故障检测仿真示意图Fig.8 With reset AR model parameters of the fault detection simulation diagram
由图4中可以看出带重置的AR模型参数故障检测算法能够在5δ以上检测到故障,且能够实现实时检测和持续报警。
5 结论
本文提出了一种基于AR模型参数的故障检测算法,利用AR模型中参数1的变化来进行导航系统故障检测,并利用实际卫星伪距新息数据进行了验证。验证结果表明其能够快速检测到小幅值突变故障,而这些小幅值突变故障利用传统的残差卡方检测是检测不到的,因此方法在实际应用中具有一定意义。
由于仿真验证是在较理想的条件下实现的,并且对于小于5δ的突变故障其检验效果也不够理想。因此下一步工作要解决如何对小于5δ的故障进行识别和判断。
[1]DEYSTJ J,DECKERTJ C.Maximum Likelihood Failure Detection Techniques Applied to the Shuttle RCSJet[J].Journal of Spacecraft and Rockets,1976,13(2):65-74.
[2]ISERMANN R.Process Fault Detection Based on Modeling and Estimation Methods A Survey[J].Automatica,1984,20(4):387-404.
[3]WILSON E.Experiments in Neural Network Control of a Free-flying Space Robot[D].Stanford:Stanford University,1995.
[4]PATTON R J,FRANK P M,CLARK R N.Issues of Fault Diagnosis for Dynamic System[M].Berlin:Springer Verlag,2000.
[5]DA R,LIN C F.Failure Detection of Dynamical Systems with the State Chi-square Test[J].Journal of Guidance,Control and Dynamics,1994,17(2):271-277.
[6]DA R,LINCF.Sensitivity Analysis Algorithm for the State Chi-squareTest [J]. Journal of Guidance.Control and Dynamics,1996,19(1):219-222.
[7]董言治,刘松涛.基于Matlab的时间序列分析和动态数据建模[J].计算机工程,2003,29(12):170~172 DONG Yan-zhi,LIU Song-tao.Time series analysis and dynamic data modeling based on matlab[J].Computer Engineering,2003,29(12):170-172.
[8]朱增锋,张鹏杰.AR模型的整体最小二乘解算及其应用[J].测绘科学2012,10(2);15-21 ZHU Zeng-feng,ZHANG Peng-jie.AR model of least square solution and its application as a whole[J].Science of Surveying and Mapping,2012,10(2):15-21.
[9]王朋辉,范胜林,刘建业.GPS/SINS超紧组合导航的性能分析[J].导航与控制,2010,9(2):1-6.WANG Peng-hui,FAN Wei-lin,LIUJian-ye.The performance analysis of GPS/SINS super tight combination navigation[J].Navigation and Control,2010,9(2):1-6.
[10]尤敏.导航系统地故障诊断技术研究[D].北京:北京航空航天大学,2002.
[11]李春科.改进的状态χ2故障检验方法及其应用[D].西安:西北工业大学,2008.
