电网电压不平衡时基于二阶广义积分器SOGI的2倍频电网同步锁相方法

闫朝阳，贺红艳，李建霞，苏 明

（燕山大学电力电子节能与传动控制河北省重点实验室，秦皇岛066004）

引言

电网同步锁相及正序分量提取是新能源并网研究中所广泛应用的技术［1］。在实现三相并网逆变器与电网同步时，最主要的方法是使用锁相环（phaselocked loop,PLL）技术［2］。 锁相环能够快速准确地检测出电网电压同步信号，即基波电压的幅值、相位及频率等。但实际情况中，三相电网电压更多是不平衡甚至畸变的，此时锁相环技术应该具备快速准确地提取电网电压正负序分量，满足频率自适应及简便等性能［3-8］。

在三相电网电压平衡时，已广泛应用的基于同步旋转坐标系的PLL（synchronous rotating frame-PLL，SRF-PLL）对电网电压正序分量的检测具有良好的特性［3］。但是在电网电压不平衡时，传统的PLL方法，会使负序分量在dq轴上产生2倍频波动，这将影响电压正序分量幅值的提取和相位角检测的准确性。

为快速准确地提取出电网电压正序分量，研究者提出了多种方法。其基本思想为，首先对不平衡的电网电压进行分离，得到电网电压正序分量，然后将其送入SRF-PLL，从而获得电网电压正序分量的相位信息［7］。文献［4］提出一种解耦双同步旋转坐标系锁相环 （decoupled double synchronous reference frame PLL，DDSRF PLL）方法，将电网电压分解到正、负序两个同步坐标系上，通过解耦网络提取基波正负序分量，由于使用了4个低通滤波器，其系统较为复杂［1］。文献［5］提出一种基于双二阶广义积分器PLL（dual second order generalized integrator PLL，DSOGI-PLL）的锁相方法。该方法利用SOGI正交发生器（SOGI-QSG）获得电网电压在两相静止αβ坐标系下的基波分量及其90°移相信号，再通过瞬时对称分量法分离出基波正负序分量，该方法能够实现频率自适应，但是SOGI-QSG输出信号的正交性对输入的直流偏置电压较敏感。

文献［6］提出一种基于延时信号对消的基波正、负序分量提取方法，利用延时信号抵消电压负序分量造成的2倍频波动，该方法正序使用的为T/4延时PLL，负序使用的为T/3和T/6延时PLL，并在正序参考电流中注入负序电流从而抑制不平衡和畸变的电网影响，但所需的缓存数据较大。文献［7］提出一种基于交叉解耦自适应复数滤波器锁相方法，能够准确估计电压正序分量及其幅值和相位信息，且无需对称分量法和大量旋转坐标变换运算，但交叉网络的存在，使得结构较为复杂。文献［8］利用陷波器（adaptive notch filter,ANF）的2个相互正交的输出量抵消SRF-PLL中由负序分量引起的2倍频波动，以此消除电网电压不对称对同步信号提取的影响；且通过ANF的输出信号可同时提取出负序分量的幅值和相位；该方法也无需对称分量法，结构较为简单，但与SOGI相似，对直流偏置量较为敏感。文献［9］提出的锁相方法是将DDSRF PLL和DSOGI相结合，使用SOGI-QSG代替Clark变换检测电网电压，然后将其送入DDSRF PLL，该方法主要用于检测频率。

本文优化了SOGI-QSG的构成，提出一种基于优化的SOGI-QSG的2倍频电网同步锁相方法，以下简称该方法为2倍频锁相 （double fundamental frequency PLL,DFF-PLL）。与传统基波锁相不同，该方法直接针对不平衡电网产生的正（负）序2倍频交流量进行锁相，然后再对电网电压正（负）序基波分量进行提取。优化的SOGI-QSG可以消除输入电压中直流偏置对SOGI-QSG输出正交信号造成的影响。2倍频锁相包含了常规SOGI的优点，与DSOGI-PLL相比，在电网电压不平衡时，2倍频锁相还能更快速准确地提取电网电压正序分量，提高锁相速度和精度。

1 三相电网电压不平衡条件下SRFPLL性能分析

SRF-PLL通过Park变换，将三相电网电压矢量从三相静止abc坐标系变换到同步旋转dq坐标系，其基本结构如图1所示［3］。通过控制q轴分量为零，使dq坐标系的旋转角度与电网电压矢量的相位角一致，从而达到追踪电网电压相位的目的。稳态时，d轴分量为电网电压相电压幅值，反馈回路输出的相位角即为电网电压的相位角。电网电压平衡时，SRF-PLL能够快速准确地追踪电网电压矢量的幅值、相位和频率；但当电网电压不平衡时，由于负序电压的存在，其检测的准确性将受到很大的影响。

图1 三相SRF-PLL结构框图

电网电压不平衡时，三相电网电压由正序、负序和零序分量构成，在三相三线制系统中电网电压可表示为

式中：V+、V-分别为电网电压基波正、负序分量幅值；ω为电网电压角频率。

经Clark变换，电网电压矢量在αβ坐标系下的表达式为

再经Park变换，电网电压矢量在dq坐标系下表示为

从式（4）可知，电网电压不平衡时，在dq坐标系下，电网电压正序分量变成直流量，而负序分量变成2倍工频交流量。正是由于负序分量引起的2倍频交流量的存在，使得SRF-PLL不能准确地提取电网电压正序分量及锁相。

2 优化的SOGI-QSG

正交信号发生器（QSG）能够从若干输入信号中提取一组所需的正交信号。本文提出的方法建立在SOGI-QSG产生的正交信号基础上，因此先对传统SOGI-QSG进行介绍，其结构框图如图2所示［5］。

图2 传统SOGI-QSG结构框图

SOGI-QSG的传递函数为

式中：v为输入信号；ζ为阻尼比；D（s）为带通滤波器传递函数；Q（s）为低通滤波器传递函数；为滤波器中心角频率。

当输入信号v含有直流分量时，由于Q（s）为低通滤波器，输出信号qv′易受直流量影响，从而影响检测正交信号幅值及电网电压相角的准确性。基于此，本文优化了SOGI的构成，通过增加求差节点，以消除正交信号中的直流分量。优化后的SOGIQSG结构框图如3所示。

图3 优化的SOGI-QSG结构框图

观察图2，可知SOGI-QSG结构中包含一个陷波器的传递函数［1,8］，即

该陷波器的波特图如图4所示。

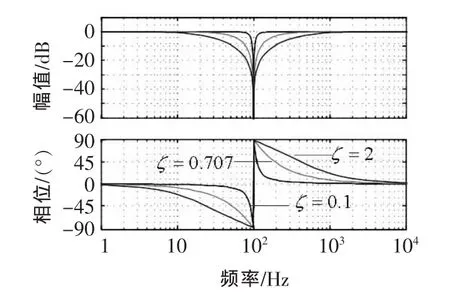
图4 ANF（s）频率响应特性与系统增益ζ的变化关系

3 新型2倍频锁相环工作原理

3.1 不平衡电网电压下正、负序2倍频交流量提取

2倍频锁相方法的提出源于式（4）中负序分量在dq旋转坐标系下产生的2倍频波动。为了提取正序分量产生的正序2倍频波动及负序分量产生的负序2倍频波动，建立了两个新的同步旋转坐标系，即正序旋转坐标系dq′+和负序旋转坐标系dq′-。需要特别注意的是，此处使用旋转坐标系的目的和文献［4］不同：本文直接对2倍频交流量进行锁相，所以需要提取由不平衡电压产生的2倍频交流量；而后者所提取的是电网电压经坐标变换后产生的直流量。因此所提方法中新建的同步旋转坐标系的变换矩阵与文献［4］也不相同。设正序旋转坐标系dq′+以角速度逆时针旋转，相位角为。电网电压经Clark变换后，在dq′+旋转坐标系下表示为

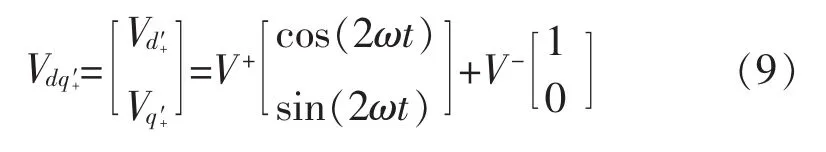
从式（9）可以看出，在dq′+旋转坐标系下，电网电压正序分量变为2倍频交流量，而负序分量变为直流量。提取出该坐标系下q轴值V+sin（2ωt），就得到正序电压2倍频交流量，从而为2倍频锁相及电网电压正序分量提取和相位检测提供条件。

同理，电网电压负序分量提取方法如下。旋转坐标系dq′-以角速度ω顺时针旋转，负序分量相位角-。电压矢量在dq′-旋转坐标系下表示为

从式（11）可知，在dq′-旋转坐标系下，电网电压负序分量变为2倍频交流量，而正序分量变为直流量。 提取出该坐标系下 q轴值-V+sin（2ωt），就得到负序电压2倍频交流量，从而为电网电压负序分量提取和相位检测提供条件。

3.2 2倍频锁相原理及电网电压正序分量的提取

2倍频锁相原理与常规SRF-PLL基本一致，其最大不同是将锁相角变成2ωt，该相角源于式（9）q轴表达式 V+sin（2ωt）中的 2ωt。V+sin（2ωt）即为不平衡电网电压正序分量产生的正序2倍频波动，该值幅值为正序电压幅值，频率为2倍电网电压频率。本文提出的方法不再对基波电压锁相而是对2倍频电压锁相，从而快速获得电网电压正序分量的幅值和相位。新型2倍频锁相方法的控制原理如图5所示。

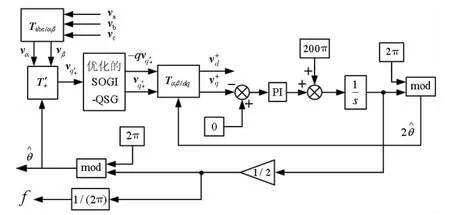
图5 新型2倍频锁相结构原理

2倍频锁相方法及电网电压正序分量的提取过程如下 ：提取dq′+坐标系下q轴 值vq′+=V+sin（2ωt）。利用优化的SOGI-QSG产生正交分量，得到正交信号 V+sin（2ωt）（vq′+）和 V+cos（2ωt）（-q vq′+）。 把这两个交流量按式（2）中 αβ 轴下的正序电压状态进行Park变换，并利用SRF-PLL对2ωt进行锁相，此时Park变换的变换角为2倍频锁相环输出角度2本质上说，对 2倍频电压V+sin（2ωt）的锁相过程，是对单相电压的锁相过程。经Park变换后的输出即为电网电压正序分量的幅值。而电网电压正序分量的相位是通过取SRFPLL输出角频率的1/2所得，即。该相位角还被用于正序2倍频交流量的提取。由2倍频锁相原理可知，在利用SRF-PLL时，锁相角变为电网电压的2倍，即2ωt，故其锁相时间可以变快。至此，正序电压的幅值和相位都已得到。

4 仿真与实验

为验证理论分析的正确性，首先使用Matlab软件进行了仿真研究，包括传统SRF-PLL、DSOGI-PLL和基于优化SOGI的2倍频锁相3种方法，以上3种方法中锁相环的 PI参数均相同：kp=0.714，ki=19.8。

当电网电压不平衡时，SRF-PLL的波形如图6所示，其中，正序分量v+=311∠0°V，负序分量v-=80∠0°V。由于负序分量的存在，使得电网电压在dq旋转坐标系下产生式（4）所述的100 Hz的波动，这使得传统SRF-PLL将不能准确提取出电网电压正序分量的幅值和相位。所以，一般先提取电网电压正序分量，然后再用SRF-PLL提取正序分量的幅值和相位。

图6 电网电压平衡跌落时SRF-PLL仿真结果

图7 为文献［5］中传统SOGI-QSG和本文优化的SOGI-QSG的输出波形仿真验证，其中，输入电压信号 v=100 cos（100 πt）+20 V。 图7（a）为采用传统SOGI-QSG的输出波形，其中qv′是含有直流分量的，其大小为 2ζεv=28.28，即输入信号中的直流量经2ζ放大后的值。图7（b）为优化的SOGI-QSG的输出波形，其中qv′已经不含直流分量。对比分析表明，优化的SOGI-QSG可以有效消除输入信号直流偏置对输出信号正交性的影响。

图8～图10为2倍频锁相与DSOGI-PLL的对比仿真结果，图中括号标2的为新型2倍频锁相值，标S的为DSOGI-PLL值。仿真时，图8与图6中的输入不平衡电压参数相同。由图可见在电网电压对称跌落时，使用2倍频锁相方法可以准确快速的提取正序幅值以及相位，且速度快于DSOGI-PLL，与理论分析相一致。对比图8（c）（d），2倍频锁相可以快速准确地提取正序电压相位角，所以图9和图10中只给出2倍频锁相的相位角。

图7 两种SOGI-QSG输出波形对比

图8 电网电压平衡跌落时仿真波形

图9 电网电压a相跌落为零时仿真波形

图9 为a相跌落为零时的仿真验证。其中a相幅值为零，b、c两相幅值相位保持不变。由图9可知，当单相电网跌落为零时，2倍频锁相环依然可以快速准确地计算出电网电压正序分量的幅值和相位，不仅速度快于DSOGI-PLL，超调量也较小。

图10为三相电网电压不平衡且初相角不为零时的仿真验证。其中，正序分量v+=311∠45°V，负序分量v-=80∠30°V。从图可知，对于初相角非零的不平衡电网电压，2倍频锁相仍可以快速准确地提取其幅值和相位。接下来进一步通过实验验证所提出的2倍频锁相方法和优化的SOGI的性能。实验中，采用DAC7625数模转换芯片输出DSP的内部变量，如三相电压正序分量的幅值、相位以及传统SOGI-QSG和优化的SOGI-QSG的输出等；采用TDS2014数字存储示波器捕获了实验波形。测试结果如图11～图14所示。

图11（a）为传统 SOGI-QSG 输出，可见 qv′是含有直流分量的，图11（b）为优化的SOGI-QSG的输出波形，可见输出的正交信号不再含直流量。

图10 电网电压不平衡且初相角不为零时仿真波形

图11 两种SOGI-QSG输出波形对比

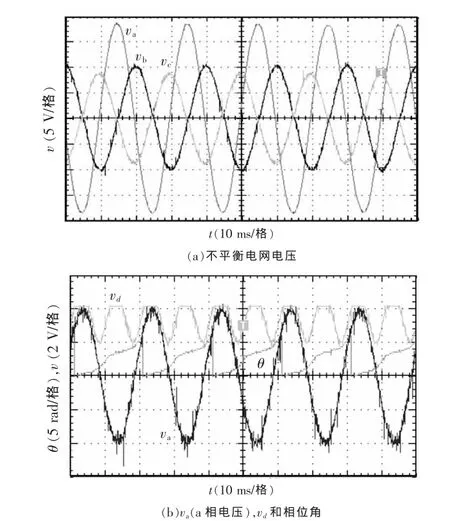
图12 三相不平衡电压时传统SRF-PLL锁相实验

图13 三相不平衡电压时DSOGI-PLL锁相实验

图14 三相不平衡电压时DFF-PLL锁相实验

图12～图14为负载输出三相不平衡电压时的锁相实验结果。图12为三相电压不平衡时，采用传统SRF-PLL锁相方法进行实验的结果。由图可见，由于三相电压负序分量的存在，传统SRF-PLL已经不能准确地提取电网电压正序分量的幅值和相位了。图13为使用DSOGI-PLL进行锁相的实验结果，可知其能够准确地提取电网电压正序分量的幅值和相位。图14为使用DFF-PLL进行锁相的实验结果，图中，-qvq′+为式（9）中 V+sin（2ωt）经优化的SOGI后的输出，即图5 中的-qvq′+。 由此可见，DFFPLL能够准确地提取电网电压正序分量的幅值和相位，且2倍频锁相的锁相频率为三相电压的2倍。至此，仿真和实验结果表明2倍频锁相方法可以快速准确地提取正序分量的幅值和相位。

5 结语

本文对电网电压不平衡情况时dq旋转坐标系下产生2倍频波动的原因进行了理论分析，并在此基础上提出一种基于优化SOGI-QSG的2倍频锁相方法，对该方法进行了理论探讨，并详细介绍了其工作原理。仿真和实验表明，所提锁相方法基于SOGI-QSG，具有SOGI的优点，能够实现频率自适应；与传统工频锁相相比，2倍频锁相法的具有较好的快速性，在一些需要快速提取正、负序分量的场合，具有一定的工程应用价值。同时研究结果表明，针对SOGI-QSG自身具有陷波器的结构特点，通过引入作差节点是能够消除直流量输入对其输出信号正交性造成的影响的。

［1］Shi L,Crow M L.Adaptive quadrant filter based phase locked loop system［C］//North American Power Symposium（NAPS）.Arlington,TX， 2010.

［2］Guo Xiaoqiang,Wu Weiyang,Gu Herong.Phase locked loop and synchronization methods for grid-interfaced converters：a review［C］//Electrical Review，2011.

［3］Chung Se-Kyo.A phase tracking system for three phase utility interface inverters［J］.IEEE Trans on Power Systems，2000，15（3）：431-438.

［4］Rodriguez P,Pou J,Bergas J,et al.Decoupled double synchronous reference frame PLL for power converters control［J］.IEEE Trans on Power Systems，2007，22（2）：584-592.

［5］Rodriguez P,Teodorescu R,Candela I,et al.New positive-sequence voltage detector for grid synchronization of power converters under faulty grid conditions［C］//IEEE Power Electronics Specialists Conference.2006.

［6］Liu Baoqi,Duan Shanxu,Liu Bangyin,et al.Compound synchronous reference frame PLL and unbalance control strategy for power conditioning system in weak grids［C］//IEEE Energy Conversion Congress and Exposition（ECCE）.2012.

［7］王宝诚，伞国成，郭小强，等.分布式发电系统电网同步锁相技术［J］.中国电机工程学报，2013，33（1）：50-55.

［8］杜雄，郭宏达，孙鹏菊，等.基于 ANF-PLL的电网电压基波正负序分离方法 ［J］.中国电机工程学报，2013，33（27）：28-35.

［9］Arezoo N，Azam B，Mohammad M，et al.Improving the decoupled double SRF PLL for grid connected power converters［C］//Power Electronics,Drive Systems and Technologies Conference （PEDSTC）.2014.