基于虚拟阻抗参数优化的并联逆变器控制研究
2014-01-15杨柳,王萍
杨 柳,王 萍
(天津大学电气与自动化工程学院智能电网教育部重点实验室,天津 300072)
引言
并联逆变器的无互联线控制方式可实现单个或少数逆变器并入或退出系统而不影响系统运行,提高了系统的冗余度和灵活性,因此越来越成为专家和学者的研究重点[1]。但是,由于逆变器间没有信息的交流,逆变器本身参数、线路阻抗、参考电压等因素的差异都可能引起逆变器间的环流流动[1]。逆变器间的环流可导致开关管损耗增大,功率器件的老化速度加快,影响系统的稳定性,甚至可能损坏开关管,增加故障率。目前解决环流问题的主要方法是利用电压幅值和频率的下垂特性来均分有功和无功功率,但是该方法忽略了逆变器等效阻抗和线路阻抗中的阻性部分,虽然对环流有一定的抑制效果,但在总体效果上不是很理想。采用诸如功率解耦、改进下垂方程等的改进方法,往往计算繁杂,环流抑制情况受参数影响过大,因此不具有一般性[2]。在逆变器中增加虚拟阻抗,可将逆变器的等效阻抗设计为呈感性或阻性,可以很好地解决上述问题[3-4]。目前虚拟阻抗的常见设计方法为:利用等效阻抗波特图的幅频相频曲线不断调整参数变化,使等效阻抗在一定频率范围内呈感性或阻性[5]。但是这种设计方法存在诸多缺点,例如逆变器本身参数发生变化时需要重新绘制波特图,设计新参数,未考虑逆变器输出电流的畸变率及环流的下降速率等。
本文通过增加虚拟阻抗的方式将逆变器的输出阻抗设计为阻性,通过逆变器等效阻抗的零极点位置变化对系统稳态及暂态性能的影响分析,提出了一种优化虚拟阻抗参数的新方法,通过对仿真结果的分析,所提方法的有效性和准确性得到有效地验证。
1 逆变器模型分析
本文逆变器采用单相全桥拓扑结构,逆变器的输出经过LC滤波之后向负载供电。为使逆变器输出电压迅速高效地跟踪参考电压,本文采用双闭环控制 (电压外环采用PI调节,电流内环采用P调节),控制框图如图1所示。

图1 逆变器的控制框图
图1 中:uref为逆变器的参考电压,kP、kI分别为电压环的比例、积分参数,kC为电流环的比例参数,kPWM为逆变桥等效的比例系数,L、r、C分别为滤波环节的电感、电阻和电容,Uo为逆变器的输出电压,io为逆变器的输出电流。
由上述框图可以得出

其中:

由式(1)可以得出,逆变器的控制与滤波部分可以等效为电压源与阻抗串联的形式,根据戴维南定理,两逆变器并联的等效电路如图2所示。
图2中,E1为逆变器1的输出电压,L1为其等效输出电感,R1为其等效输出电阻,Io1为输出电流。E2为逆变器2的输出电压,L2为其等效输出电感,R2为其等效输出电阻,Io2为输出电流。Z为负载,Uo为负载电压,Iz为负载电流。

图2 并联逆变器的等效模型
逆变器间的环流量是一个人为定义的旨在观察环流大小的量,在实际电路中不能直接测量得到,但是它能够直接反映逆变器的功率均分情况,其定义公式为

由式(4)可以看出,环流的大小与逆变器输出的电压差(幅值、相位)成正比,与其等效输出阻抗成反比。因此,抑制环流的主要措施为:减小逆变器间的电压差,增大等效输出阻抗。
2 逆变器等效阻抗分析
由式(3)可得,逆变器的等效输出阻抗受滤波参数、电压电流环控制参数等多因素影响,这些因素的差异导致了并联逆变器间的参数不一致,从而在并联逆变器间产生了环流。而且等效阻抗往往很小,因此如果不采取必要的控制措施,有可能产生较大的环流,甚至损坏逆变器。与此同时,扰动的突现、负载突变等情况不仅要求并联逆变器能够将环流迅速降低至合理范围,而且要求并联逆变器能够避免动态时刻的环流峰值过大,损坏开关管的情况发生。加入虚拟阻抗可有效地解决上述问题,逆变器控制框图如图3所示。

图3 加入虚拟阻抗的逆变器控制框图
由上述系统框图可得

设计方案为

将式(7)带入式(6)中可得

传统虚拟阻抗的参数Rv和Kv利用波特图的幅频和相频波形选取[5],其选择一般以稳态性能为主,动态性能往往被忽略。图4为利用传统方法选取虚拟阻抗参数的逆变器等效阻抗的阶跃响应,其中 L、r、C 分别取 10 mH、0.2 Ω、4.7 μF,主要控制参数 kP、kI、kC分别取 0.5、1 000、30。
由图4可以看出,传统利用虚拟阻抗进行控制的逆变器等效阻抗的阶跃响应振荡幅度和超调量很大,响应时间长,这使得在扰动突现或负载突变时,瞬时环流峰值过大,环流下降速度过慢等现象可能出现,有可能损坏开关管。选取传统虚拟阻抗参数[6],对应的零极点坐标如图5所示。逆变器等效阻抗的传递函数存在3个极点(一个实数极点,2个共轭极点)、2个零点 (一对共轭零点),3个极点均在虚轴左侧,保证了系统的稳定性,两个共轭极点离虚轴最近,可看做主导极点,共轭主导极点的存在使系统的暂态响应呈振荡性质,另一个实数极点的实部值小于5倍主导极点的实部值,因此影响不能忽略。由于它的存在,系统阻尼增大,使响应速度减慢。但是共轭零点的存在使得超调量增加,零点与虚轴距离越近作用越明显[7]。因此为解决上述问题,等效阻抗的控制措施必不可少。

图4 传统方法的逆变器等效阻抗的阶跃响应
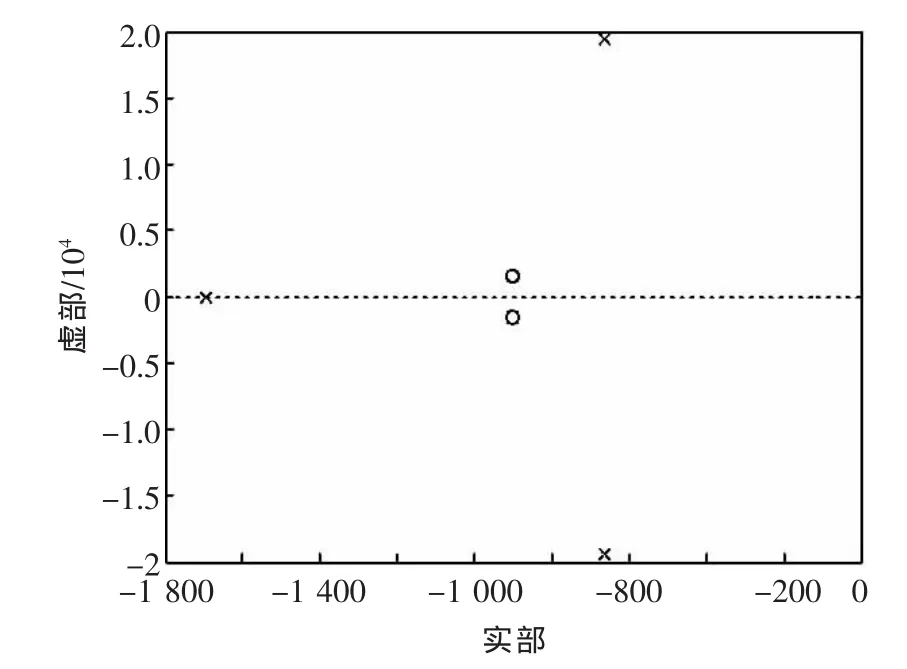
图5 传统方法的逆变器等效阻抗的零极点坐标
本文采用的优化措施为:保留主导极点,利用偶极子降低实数极点的影响。
利用式(9)对等效阻抗的分子降阶,减少一个零点,减小超调量。

假设等效阻抗的实数极点为P0,由式(8)可得

利用式(9)和式(10)确定 Rv和 Kv,其对应的逆变器等效阻抗的零极点坐标如图6所示。

图6 优化方法的逆变器等效阻抗的零极点坐标图
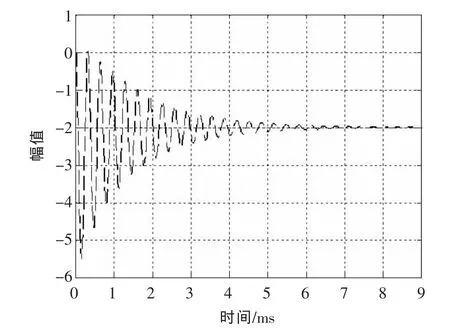
图7 优化方法的逆变器等效阻抗的阶跃响应
由图6可知,3个极点没有变化,Rv和Kv的合理选择使得一个实数零点非常靠近实数极点P0,其相互距离比其本身的模小一个数量级以上,可被视为偶极子。该偶极子的位置远离原点,因此它对系统暂态影响可以忽略,即该零点补偿了实数极点对响应速度的影响,加快了响应速度。另一个零点由于距离虚轴非常远,其影响可以忽略不计。因此,该系统可被等效为二阶系统,暂态响应由主导极点决定。图7为对应的阶跃响应,对比图4和图7可得,本文的优化方法使得振荡明显减弱,调整时间变短,超调量大幅降低,改善了系统的动态性能。

图8 传统方法和优化方法的阶跃响应对比

图9 传统方法和优化方法的的波特图对比
图8 和图9分别为传统方法和优化方法的逆变器等效阻抗的阶跃响应对比和波特图对比图。如图8和图9所示,加入虚拟阻抗后,逆变器的等效阻抗在一定范围保持呈阻性,但是与传统方法相比较,本文所用方法使得闭环频率呈阻性的带宽增大,相应时域响应的调整时间缩短,幅频特性的谐振峰值减小,相应时域响应的最大超调量减小,佐证了本文方法的有效性。
3 仿真结果
本文在Matlab仿真平台上搭建了两台逆变器并联的模型,额定容量为1 kVA,载波频率为20 kHz,通过LC滤波,分别在参考电压不同和逆变器并入退出系统等条件下进行仿真实验,观察使用传统虚拟阻抗方法和本文所用方法下的逆变器输出电流及环流的波形(实线代表逆变器1的输出电流波形,虚线代表逆变器2的输出电流波形,点线代表逆变器间的环流)。
3.1 参考电压不同时输出电流及环流波形
图10、图11分别为参考电压有差异 (Uref1max=311.05 V,Uref2max=311 V)时,传统方法和优化方法在加入虚拟阻抗(t=0.05 s)后的逆变器输出电流及环流波形。

图10 传统方法的逆变器输出电流及环流

图11 优化方法的逆变器输出电流及环流
对比图10和图11可以看出,由于逆变器参考电压的不同,若不加虚拟阻抗控制,逆变器间存在环流,环流不随运行时间减弱,其峰值可达0.34 A左右,在0.05 s加入传统方法设计的虚拟阻抗,环流下降速度非常缓慢,大约经过0.13 s环流才逐渐下降为接近于零值,若长期运行,将加快功率器件的老化速度,增加故障率。对比本文所用的优化方法,在0.05 s加入虚拟阻抗,环流迅速下降为接近于零值,大幅降低了响应时间,验证了上述理论的有效性。
3.2 逆变器并入退出系统时输出电流及环流波形的比较
图12和图13分别为逆变器并入退出系统时,传统方法和本文所用优化方法对逆变器输出电流及环流波形的影响 (t=0.05 s前逆变器1单独带负载运行,t=0.05 s时刻逆变器2并入系统,两逆变器同时带负载运行,t=0.15 s时逆变器1退出系统,由逆变器2单独带负载运行)。

图12 传统方法的逆变器输出电流及环流

图13 优化方法的逆变器输出电流及环流
对比图12和图13可以看出,在逆变器2并入系统后,传统方法对逆变器并入系统的环流抑制情况不理想,环流一直保持在0.6 A左右,没有降低的趋势,长期运行对于开关管损伤很大。而本文所用方法使得环流在很短的时间内降低为接近于零,并入时刻未出现环流尖峰,两逆变器能够共同稳定运行,其动态性能和稳态性能都达到了理想要求,验证了本文方法的有效性。
4 结语
本文通过对逆变器等效阻抗的零极点位置变化对系统稳态及暂态性能的影响分析,给出了一种优化虚拟阻抗参数的新方法。利用Matlab分别在参考电压不同和逆变器并入退出系统等条件下进行仿真实验,对比传统方法和本文所用方法的逆变器输出电流和逆变器间环流的波形,可以得出结论,本文所用方法能够降低瞬时环流峰值,加快环流下降速度,降低输出电流畸变率,有效地改善了逆变器的动态及稳态性能,提高了多逆变器并联运行的稳定性。
[1]王尚.微网中光伏逆变器并联技术研究[D].哈尔滨:哈尔滨工业大学,2013.
[2]阚志忠,张纯江,薛海芬.微网中三相逆变器无互连线并联新型下垂控制策略[J].中国电机工程学报,2011,31(33):68-74.
[3]He Jinwei,Li Yunwei.Analysis,design,and implementation of virtual impedance for power electronics interfaced distributed generation[J].IEEE Transactions on Industry Applications,2011,47(6):2525-2538.
[4]张宇,余蜜.模块化UPS采用虚拟阻抗的瞬时均流控制方法[J].中国电机工程学报,2012,32(21):8-14.
[5]路嘉鑫,张颖超,钱希森,等.逆变器无线并联虚拟阻抗分析[J].电源学报,2014(1):54-60.
[6]陈燕东,罗安,龙际根,等.阻性逆变器并联环流分析及鲁棒下垂多环控制[J].中国电机工程学报,2013,33(18):18-29.
[7]翁贻方.自动控制理论[M].3版.北京:机械工业出版社,2007.
[8]He Jinwei,Li Yunwei.Analysis,investigation and active damping of multiple resonances in a parallel-inverterbased microgrid[J].IEEE Transactions on Power Electronics,2013,28(1):234-246.
[9]吕志鹏,罗安.不同容量微源逆变器并联功率鲁棒控制[J].中国电机工程学报,2012,32(12):42-49.
[10]Yao Wei,Chen Min,Matas J,et al.Design and analysis of the droop control method for parallel inverters considering the impact of the complex impedance on the power sharing[J].IEEE Transactions on Industrial Electronics,2011,58(2):576-587.
[11]Zhang Yu,Yu Mi,et al.Instantaneous current-sharing control strategy for parallel operation of UPS modules usingvirtualimpedance[J].IEEETransactionsonPowerElectronics,2013,28(1):432-440.
[12]Vasquez J C,Guerrero J M,et al.Modeling,analysis,and design of stationary-reference-frame droop-controlled parallel three-phase voltage source inverters[J].IEEE Transactions on Industrial Electronics,2013,60(4):1271-1280.
[13]于玮,徐德鸿.基于虚拟阻抗的不间断电源并联系统均流控制[J].中国电机工程学报,2009,29(24):32-39.
[14]He Jinwei,Li Yunwei,et al.Generalized closed-loop control schemes with embedded virtual impedances for voltage source converters with LC or LCL filters[J].IEEE Transactions on Power Electronics,2012,27 (4):1850-1861.
[15]Guerrero J M,Vasquez J C,Matas J,et al.Hierarchical control of droop-controlled ac and dc microgrids:a general approach toward standardization[J].IEEE Transactions on Industrial Electronics,2011,58(1):158-172.
