直驱风电系统三电平变流器的设计与仿真
2014-01-15杨国良张恩贝方一鸣
杨国良,张恩贝,方一鸣
(燕山大学电力电子节能与传动控制河北省重点实验室,秦皇岛066004)
引言
随着风电机组单机容量的不断增大,风电变流器的电压与电流等级也在不断提高,因此多电平变流器拓扑得到了广泛关注。变流器采用多电平方式后,可以在常规功率器件耐压基础上,实现高电压等级,获得更多级(台阶)的输出电压,使波形更接近正弦,谐波含量少,电压变化率小,并获得更大的输出容量。因此直驱风电型多电平变流器是现在将来风电发展的主流趋势。
基于电压型三电平逆变电路的多电平逆变电路,特别是三电平逆变电路已进入实用化阶段,对其进行研究和分析很有实际意义。一般认为多电平逆变器是建立在三电平逆变器的基础上,按照类似的拓扑结构拓展而成的。电平数越多,所得到的阶梯波电平台阶越多,从而越接近正弦波,谐波成分越少。但这种理论上可达到任意N电平的多电平逆变器,在实际应用中由于受到硬件条件和控制复杂性的制约,通常在追求性能指标的前提下,并不追求过高的电平数,而以三电平最为实际。国外也有对七电平及更高电平的研究,但都还不成熟,特别受硬件条件和控制性能的限制,还处于理论研究阶段。目前三电平逆变器的主要控制方法有消谐波PWM法,开关频率最优PWM法和空间矢量PWM法等。控制方法的研究是三电平逆变器研究的一个热点问题。
1 二极管钳位式三电平逆变器拓扑结构分析
三电平逆变器的各种拓扑结构都有一些共同优点,如适合大容量、高电压变频场合,由于开关器件在较低的工作频率下可以获得较好的波形,因此开关损耗低,效率高,电路的电磁干扰(EMI)问题大大减轻等。
图1给出了一种三电平逆变电路,为中点钳位型(neutral point clamped)逆变电路,开关器件选用IGBT,电路的每相桥臂有4个开关元件、4个续流二极管和两个钳位二极管。两个串联器件的中点通过钳位二极管和直流侧电容的中点相连接。钳位二极管在开关管导通时提供电流通道防止电容短路。

图1 二极管钳位式三电平逆变器主电路
(1)开关管S1和S2同时导通时,S3和S4同时关断,若电流从逆变电路流向负载,即从p点经由S1和S2到达输出端a,忽略开关器件的正向导通压降,输出端a的电位等同于p的电位,即Vdc/2;若电流从负载流向逆变电路,这时电流从a分别经过D12、D11流进p点,这时输出端a的电位仍等同于p 的电位,如图2(a)所示。
(2)开关管 S2和 S3同时导通时,S1和 S4同时关断,若电流从逆变电路流向负载,即从中性点o点经由D1和开S2到达输出端a,输出端a的电位等同于o点的电位,即0电位;若电流从负载流向逆变电路,这时电流从a分别经过S3和D2流进o点,这时输出端a的电位仍等同于o点的电位,如图2(b)所示。
(3)管S3和S4同时导通时,S1和S2同时关断,若电流从逆变电路流向负载,即从负电位n点分别经过D21、D22到达输出端a,输出端a的电位等同于n的电位,即-Vdc/2;若电流从负载流向逆变电路,电流从输出端a分别经过S3和S4流进n点,忽略开关器件的正向导通压降,这时输出端a的电位仍等同于 n 的电位,即-Vdc/2,如图2(c)所示[3]。


图2 三电平逆变器相电压3种输出电平
需要注意的是,S1和S4不能同时导通,S1和S3、S2和S4工作在互补状态,平均每个主开关管所承受的正向阻断电压为Vdc/2,这也是三电平逆变器的基本控制规律之一[4]。
三电平逆变器的驱动控制基本原则如下:对应于a(b,c)相的3种状态,为了保证每次输出状态变化过程中动作的开关器件最少,该相电位不能在Vdc/2和-Vdc/2之间直接变化,表1给出了a相电位发生变化时,功率开关器件的工作状态。在设计时,其硬件及软件设计应遵循表1规律(“-”表示关断,“+”表示导通)。
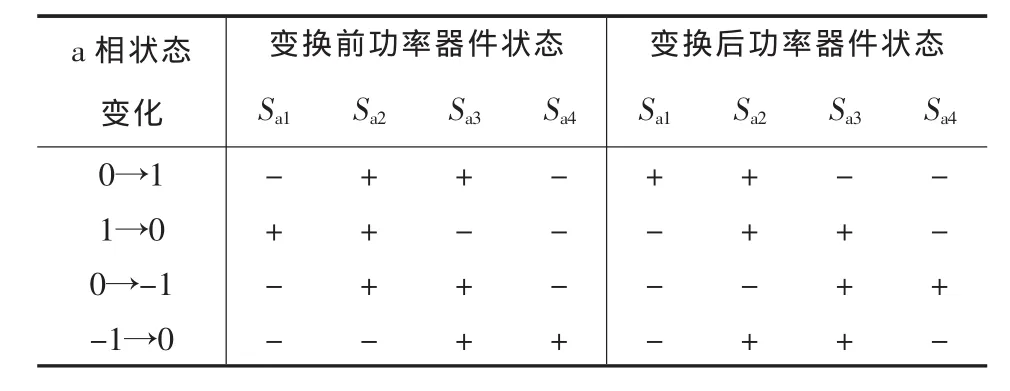
表1 a相开关工作状态
2 三电平逆变器SVPWM算法
2.1 区域判断
区域判断的目的主要是找出合成参考电压矢量的3个基本矢量。传统算法根据三电平基本空间矢量图将整个矢量空间先分成6个大扇区,每个扇区在空间占60°。再将每个大区域分成4个小区域。
由于基本空间矢量中的短矢量在每个采样周期中出现的次数多,为了算法及仿真的准确性,故将每个大区域细分成6个小区域。按照这样的划分方法,三电平SVPWM算法的扇区划分和小区域划分分别如图3和图4所示。Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ表示各个大扇区用 1、2、3、4、5、6 表示小区域。

图3 三电平SVPWM算法的扇区划分
因为大区域按照矢量角度每60°为一区划分,因此可以按照参考电压矢量的角度判断其所在的大区域。根据小区域的区域分布情况和几何关系可以按照以下方法判断参考电压矢量所在的小区域[9]。
以第Ⅰ大区为例,如图4所示,参考电压矢量Vref在α轴和β轴上的投影分别为Vα和Vβ,幅角为θ,则有
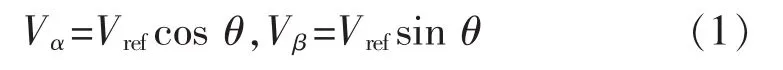
(1)当θ≤30°时,Vref在小区域1或3或5内。 若则Vref在小区域1内;若则Vref在小区域 5内;否则,Vref在小区域3内。
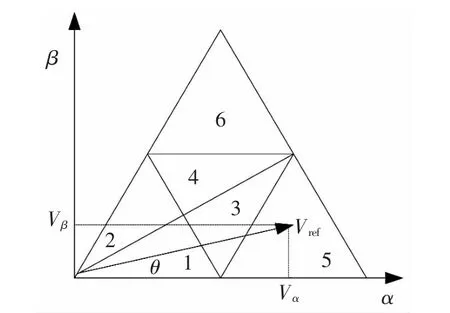
图4 小区域判断
(2)当θ≥30°时,Vref在小区域2或4或6内。若则Vref在小区域2内;若,则 Vref在小区域 6 内;否则,Vref在小区域4内。
2.2 时间计算
判断出参考电压矢量所在的区域,根据NTV(nearest triangle vector)法则,也就找到了合成参考电压矢量的3个基本矢量V1、V2、V3,连同参考电压矢量Vref一起,代入伏秒平衡方程组得

解出 T1、T2、T3即完成了三电平 SVPWM 算法对基本空间矢量作用时间的计算。如以Ⅰ大区4小区为例,则有
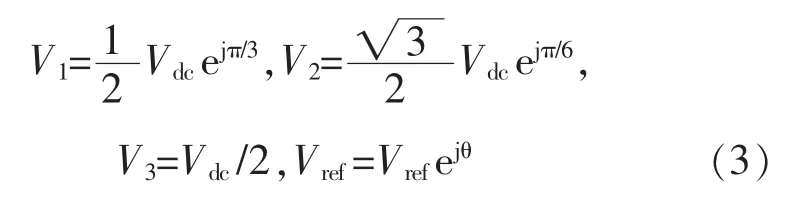
将其代入伏秒平衡方程组得

此方程按实部,虚部分开后得

解得 T1、T2、T3分别为
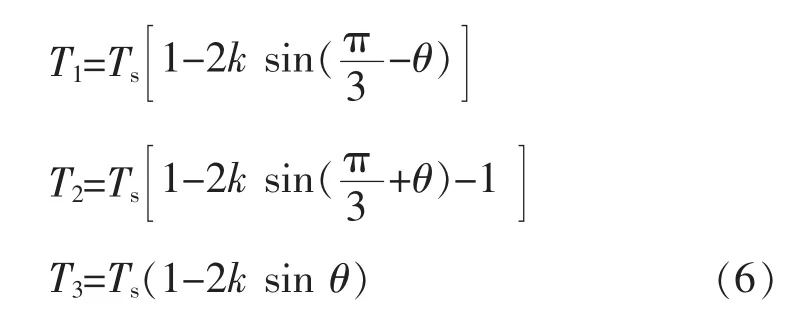
3 三电平逆变器中点电压波动定性分析
由图5所示,电容C1、C2为直流分压电容。由于电容电压没有被恒流源所固定,因此中点电位是波动的,且其值的改变正比于中点电流。若不考虑负载,各开关状态与中点电流的情况密切相关,并且可以描述为以下4种情况:
零矢量状态(如 000,111,-1-1-1)时,由于没有电流流过中点,所以不会引起中点电位的波动。
大矢量状态(如 11-1,-1-11,等)时,由于每相的终端直接连在直流侧的正端或负端,因此中点电位不会受影响,如图5(a)和(b)所示。
中矢量状态(如10-1)时,由于有一相的终端直接连在中点,所以会引起中点电位平衡的改变。如图5(c)所示。
小矢量状态(如110)时,至少有一相连在中点,因此也会影响中点电位的平衡。由于小矢量的存在都是以成对方式出现的,比如110和00-1,它们的输出电压相同但是对中点电位的影响相反。如图5(d)~(g)所示。


图5 中小矢量与中点电位的关系
图5 为各矢量开关状态的等效电路,其中M代表负载。由图5可以看出中小矢量时均有电流从负载流入两电容之间或从两电容流向负载。电流的流入与流出必将引起两个电容冲放电。当电流流入中点时,中点电位将升高;当电流流出中点时,中点电位将降低[17]。
4 仿真验证
完整的仿真模型如图6所示。
三电平SVPWM逆变器模块主要有电压3/2变换模块、扇区判断与角度计算模块、区域判断与调制比模块、作用时间判断模块、时间分配模块和SVPWM输出模块组成。
三相电压首先在Subsystem4中经过3/2变换到两相静止坐标系,再在Subsystem5中进行大扇区判断并计算出角度,在Subsystem中判断电压矢量所在的小区域,随后在Subsystem3内计算出作用时间,在Subsystem1中对时间进行分配,在Subsystem2中产生触发脉冲,根据Vector Status和Switch Status中的开关表对主电路开关管进行触发。
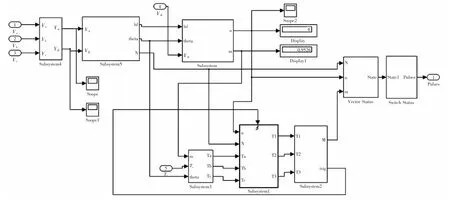
图6 三电平逆变器SVPWM仿真模型
4.1 大扇区判断
该模块主要包含两个功能:通过参考矢量的角度判断其所在的大扇区N;将参考矢量的角度转换为第一扇区中对应的角度,仿真模型如图7所示。
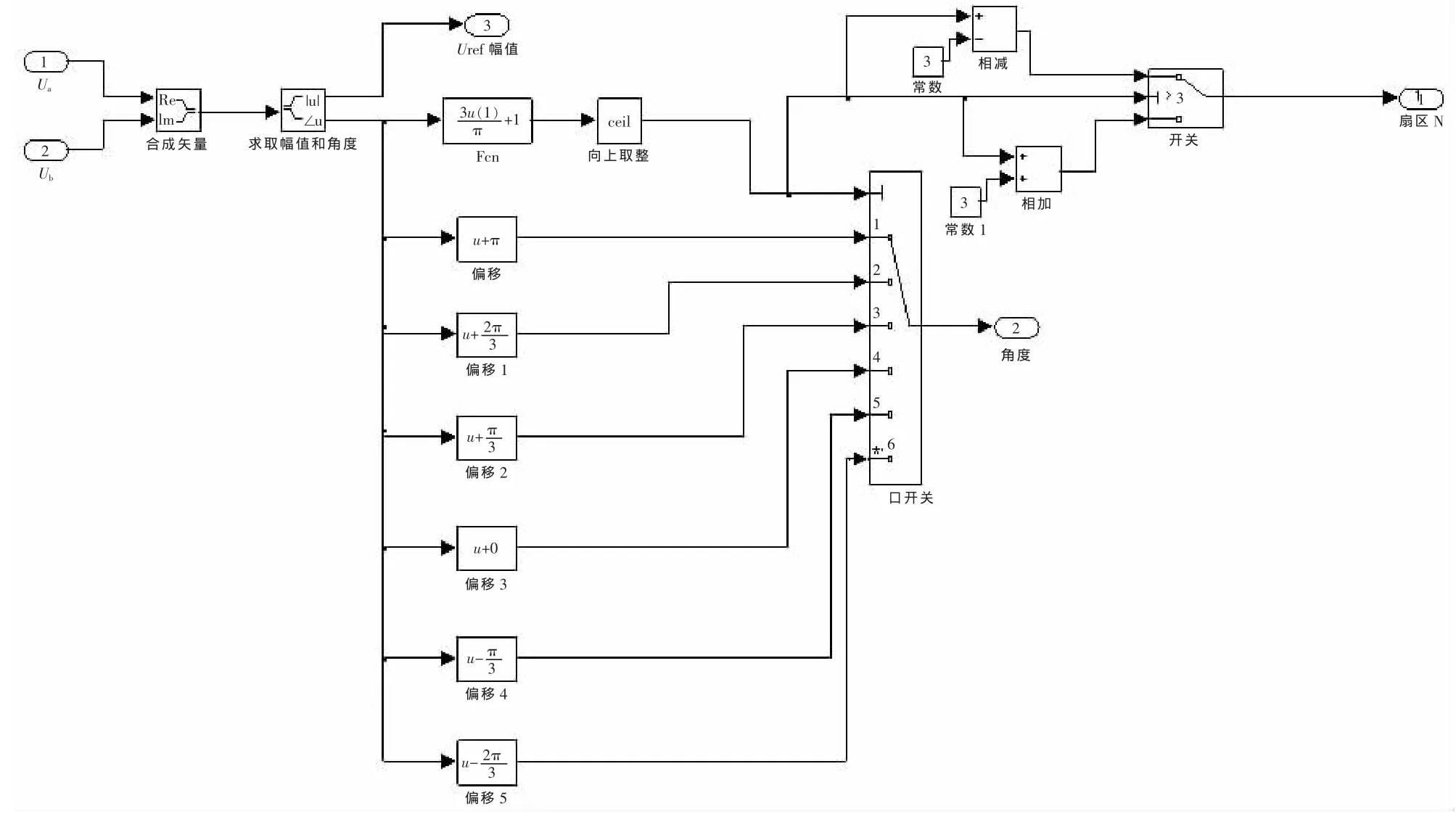
图7 大扇区判断模型
4.2 小区域判断
小区域判断模型如图8所示,按照上文区域判断部分中所述传统三电平SVPWM算法判断小区域时的逻辑关系直接搭建仿真模型。判断时按照假设条件逐层递进,直到判断出参考矢量仿真结果。
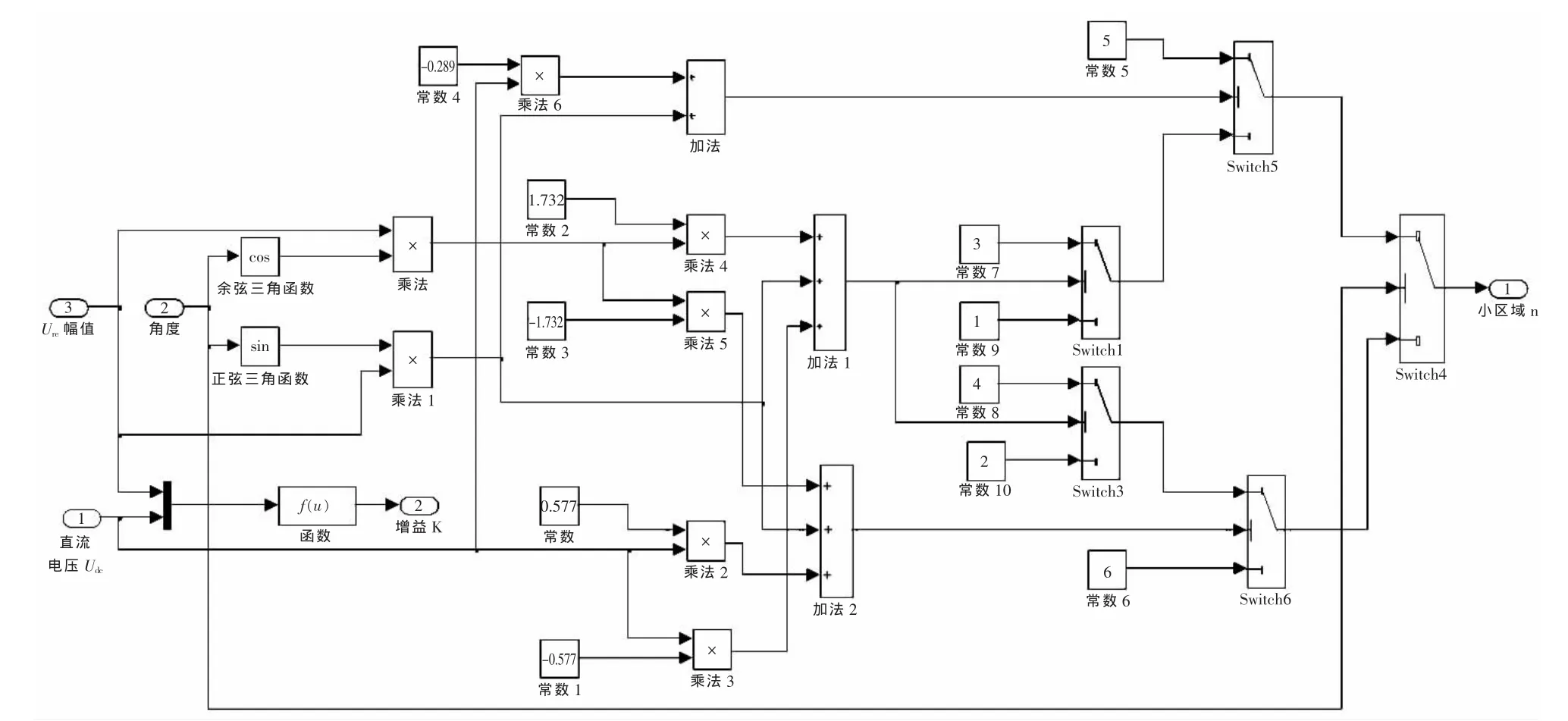
图8 小区域判断模型
4.3 仿真结果
仿真参数设置如下:直流母线电压为600 V,载波频率为50 Hz,开关频率为1 000 Hz。负载部分采用三相对称负载代替电机,电阻R=4 Ω,电感L=20 mH。仿真结果如图9~图12所示。

图9 a相电流仿真结果

图10 小区域仿真结果

图11 a相电压仿真结果

图12 ab两相线电压仿真结果
5 结语
对三电平逆变器的SVPWM的常规算法进行了详细的分析和推导,随后对该方法进行了改进,设计了易于实时实现的SVPWM算法。仿真结果表明,该算法能输出期望的三电平线电压波形,所采用的中点电位控制方法能在很大程度上减小中点电压的波动,而且实现起来也非常容易。
[1]李东林,陈陈.风论发电机组动态模型研究[J].中国电机工程学报,2005, 25(3):115-119.
[2]李建林,朱颖,胡书举,等 .风力发电系统大功率变流器的应用[J].高电压技术,2009, 35(1):169-175.
[3]李永东,肖曦,高跃.大容量多电平变换器[M].北京:科学出版社,2005.
[4]刘毅,谭国俊,李渊.基于双三电平变流器永磁直驱风电系统[J].电机与控制应用,2011, 38(4):37-41.
[5]廖鄂,周国荣.变频恒速风力发电系统三电平SVPWM逆变控制[J].机械工程及其自动化,2012,160(4):128-130.
[6]尹明,李庚银,张建成,等.直驱式永磁同步风力发电机组建模及其控制策[J].电网技术,2007,31(15):61-65.
[7]王斌,王峰,刘毅,等.双三电平永磁直驱风力发电系统控制策略研究[J].电力电子技术,2011,45(8):70-72.
[8]Raza K S M,Goto H,Guo Hai-Jiao.A novel algorithm for fast and efficient maximum power point tracking of wind energy conversion systems[C]//Proceedings of the 2008 International Conference on Electrical Machines.2008:1-6.
[9]Sahin A D.Progress and recent trends in wind energy[J].Progress in Energy and Combustion Science,2004,30(5):501-543.
