多修路，就能解决交通拥堵问题吗？

曹志刚

现在堵车简直成了所有城市共同面临的问题，大城市的拥堵自不必说，连三线城市都开始堵车了。当我们被堵在路上的时候总会想：要是多修几条路的话，就不会这么堵了吧？事实真的如此吗？

看似最快捷的路线

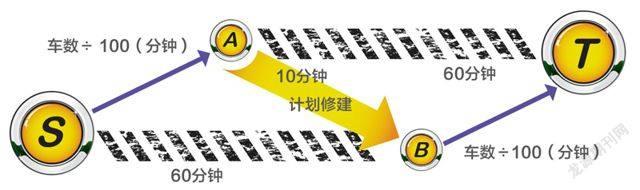
为了研究这个问题，我们设计了一个简化的交通模型。假设每天有4000人开车从S地到T地去上班。目前有两条线路供选择：S—A—T和S—B—T。公路S—B和A—T都比较宽阔，固定耗时60分钟；公路S—A和B—T则比较窄，耗时由行车数目决定，为车数除以100（分钟）。

如果是随机选择路线的话，时间长了就会摸索出规律，最终的结果是走S—A—T和S—B—T两条路线的人均为2000人，每个人花费的总时间也都是80分钟。用学术术语来说，这就是唯一的一个均衡结果。我们用博弈论来预测一定是这个样子。

如果有一天，政府计划在A与B之间修建一条快车道。真的很快，只需要10分钟！这会带来什么变化？交通拥挤是不是会缓解了呢？

以前走S—A—T路线的人会很高兴：因为原来从A到T需要60分钟，现在先走A—B快车道，再从B到T，最多是10分钟+4000/100分钟=50分钟，至少节约10分钟！所以这些人都会改走S—A—B—T路线。

以前走S—B—T路线的人也会很高兴：因为原来从S到B需要60分钟，现在先从S到A，再走A—B快车道，最多是4000/100分钟+10分钟=50分钟，至少节约10分钟！所以这拨人也会改走S—A—B—T路线。

好啦，我们已经分析出来大家都会走S—A—B—T路线。用学术术语来说，这是一个新的均衡。而且皆大欢喜，似乎大家在新均衡下都比旧均衡下少用了10分钟。且慢，真的是这样吗？让我们再来算一下。如果4000个人都走S—A—B—T路线，那么每个人的总时间应该是4000/100分钟+10分钟+4000/100分钟=90分钟，这比原来还慢了10分钟呀！

布雷斯悖论来解释

究竟是哪种计算正确呢？究竟是变快了还是变慢了？仔细想想就会发现其实是第二种。因为在第一种分析里，原来选择S—A—T路线的人计算自己节约时间的时候没有预料到其实另外的人有可能会从S—B转到S—A，而原来选择S—B—T路线的人也没有考虑到有人会从A—T转到B—T。但是所有人都选择S—A—B—T的确是唯一的新均衡！在这个状态下，没有人愿意改变路线。所以不算不知道，一算吓一跳。恰恰因为多修了一条路，每个人都要为此而多花费10分钟！

上述现象是由德国数学家布雷斯（Braess）于1968年首次发现的，我们现在称之为“布雷斯悖论”。现在有一项相关的科学研究叫“自私路由问题”，是算法博弈论领域的一个前沿研究方向，在交通和互联网路由方面都有重要应用。

聪明的读者可能会问，如果真是这样子的话，那么大家都约定不去走A—B这条近路，而按照原本选择的路线继续行进不就没有问题了吗？这样尽管多修了一条路没有改善交通，但也不至于让交通变得更糟糕呀！这就涉及到博弈论中的一个经典话题，“囚徒困境”和“集体行动的逻辑”。在某些情况下，合作是件非常困难的事情。说起来容易做起来难呀，即便是有一个好办法能让大家都变好，也可能很难实施。每个人都为一己之私着想，每个人做出了一个看起来都聪明无比的决策，却不去想这样做会损害别人，最终大家相互损害，达到一个谁都不愿意看到的悲催局面。

生活中的案例

你会不会认为前面举的例子只是一个数学游戏，仅仅存在于数学家的想象中，现实中绝不可能发生呢？那么亲爱的读者，你又错了！这样的例子还真有。在德国的斯图加特，人们为了改善交通新修了道路，结果却造成了更加严重的堵车，最后不得不废弃了这条新修建的公路。在 1990 年的世界地球日，纽约市决定关闭第 42 号大街。对堵车泛滥成灾的纽约市来说，这个消息简直是晴天霹雳。就在大家都期待着发生超级大堵车的时候，交通状况反而难以置信地比平时有所好转！同样的事情在韩国首尔的清溪川改造工程中也曾经发生过。

当然，现实的城市交通状况极为复杂，会受到很多因素的综合影响，并不是简单的多一条路少一条路的问题。布雷斯悖论所描述的，也只是一个极端情况。科学家们后来还发现，即便出现了布雷斯悖论，在车流量继续增加的情况下，交通状况也会有所恢复，布雷斯悖论将被打破。也就是说，布雷斯悖论只有当车流量在一个固定范围内时才有可能出现。所以大家请不要太担心，数学家发现的布雷斯悖论这个“魔鬼”只会在很少的情况下才会困扰我们。

（责任编辑/冷林蔚 刘阳）