地学G4I 系统集成数据质量评价关键技术研究

魏红雨，路来君，郝 满，郝琳琳

(1.吉林大学a.地球科学学院，长春130061;b.计算机科学与技术学院，长春130012;2.黄河水利职业技术学院水资源工程系，河南开封475003)

0 引言

4G地学空间数据是指地质学(Geology)、地理学(Geography)、地球化学(Geochemistry)、地球物理学(Geophysics)数据。地学G4I(Geology Geography Geochemistry Geophysics Information)系统是由吉林大学开发的具有自主知识产权的，以4G数据库互操作为基础，以地学数据集成、矿产资源评价为主要内容，服务矿产资源精确预测的专用GIS(Geology Information System)系统［1］。随着地学G4I系统研究应用的不断深入，4G地学空间集成数据在表达空间数据的位置特征、时间特征和属性特征时，能实现的完整性、准确性、一致性和统一性等指标程度，即数据质量问题，越来越引起广泛关注。利用数据质量评价技术，对4G地学空间集成数据质量进行定性和定量分析，是实现数据质量控制的基本前提。传统层次分析法(AHP:Analytic Hierarchy Process)［2］在进行数据质量评价过程中，由于各层次指标采用人工比较赋值的方法，主观性较强，对结果影响较大;如何改进AHP赋值方法，提高评价结果的客观性是当前研究数据质量控制的关键技术之一。

1 层次分析法

层次分析法是一种定性和定量分析相结合的系统化、层次化的决策分析方法［3，4］。其核心内容是:合理分层，优先权重，构建递阶层次关系。应用层次分析法进行决策判断的基本思路是:将定性的分析过程层次化、数量化，并用数学方法为分析、决策、控制提供定量依据。其基本原理是:通过分析问题的性质和解决问题要达到的目标，将问题划分成各种因素，按照支配关系，形成递阶的层次结构;通过比较的方式确定各因素间的相对权重;通过逐层计算的方式得到综合计算值，进而得到总目标的计算值。应用层次分析法分析解决问题的基本步骤为:建立层次结构模型，将有关因素按照不同属性自上而下分解为若干层次，自上而下分别为目标层、准则(指标层)和方案层，各层对上对下都有相应的支配隶属关系(见图1);构造成对比较矩阵，自层次结构模型的第2层开始，将从属于同一上层因素的同层诸因素进行两两对比，比较二者相对上层因素的权重(设指标i与j是隶属于同一上层指标的同层指标，将i与j相对于同一上层指标的重要程度进行比较)，并用1～9比较尺度标记(见表1)，构造比较矩阵，直至最下层;计算权重并做一致性检验，计算每个对比矩阵的最大特征值及特征向量，检验一致性，判别特征向量是否为合适的权重向量;计算组合权向量并做组合一致性检验，计算最下层因素对目标层的组合权向量，根据公式做组合一致性检验，判定构造的对比矩阵权重的合理性。

图1 层次分析法模型Fig.1 Analytic hierarchy process model

表1 指标比较权重1～9标度表Tab.1 1～9 Scaling of the index comparative weight

层次分析法是对决策者的经验判断进行量化的一种分析决策方法，适合在目标结构复杂且缺乏必要数据的情况下使用。当问题的分析过程涉及大量相互关联、相互制约的复杂因素以及各因素对问题的重要性不同时，可用层次分析法分析解决。所以，层次分析法是典型的多指标综合评价方法。

层次分析法能利用较少的定性信息使决策过程数学化，较方便地实现定性到定量的转换，能为多准则、无结构特性的复杂决策问题提供决策方法，适合于对决策结果难以直接准确计算的系统评估，具有简单明了的优点。但层次分析法也存在明显的缺陷。层次分析法的作用是确定指标对目标的权重或进行优劣排序，是一个选优过程，其缺陷主要表现在:1)因为层次分析法本身是基于主观评价的，所以在应用层次分析法时很容易因为主观因素改变评价结果;2)指标数多少的确定会对评价结果产生重大的影响;3)指标的权重确定也是一个不断调整的过程，需要经过反复的运算和改进过程才能不断趋于完善，且最终的结果只要求在可接受范围内，不一定是最佳值。

2 改进的层次分析法

典型的层次分析法在确定指标层指标和方案层指标时，默认下层因素对上层聚合时采用加权求和的方法［5，6］。加权求和的方法能表现出属于同一上层指标的同层指标对上层的影响程度，即权重大的指标对上层的影响大，权重小的影响小。但加权求和法不能反映同层指标对同一上层指标存在的必要程度，即指标的存在对上层具有的绝对意义。即应用典型的层次分析法只体现了下层指标存在的充分性而没有体现存在的必要性。为描述下层指标对同一上层指标的绝对影响，体现指标存在的必要性，引入对层次分析法的改进办法，采用加权求积的方法，反映下层对上层的绝对影响。该方法假设下层指标与同一上层指标之间的关系为“与”关系，下层指标聚合到上层时采用加权求积的办法。改进的层次分析法的层次分析模型如图2所示。

分析量化及指标赋值的步骤与典型的层次分析法相同，但加权求值时采用相与的方法。典型层次分析法经过改进能更合理地反映下层因素对总目标的影响。改进的层次分析法具有层次分析法的特点，是一种更适合系统分析的定性评价与定量评价相结合的方法。改进的层次分析法在实施过程中可选定对结果有效的多个指标综合分析，采用模糊数据中的隶属度理论实现定性评价与定量评价之间的转化，具有模糊综合评价法和多指标综合评价法的优点。改进的层次分析法采用下层指标对上层指标的加权求积的方式，跟缺陷扣分法的思路相同。因此，改进的层次分析法更适合4G地学空间集成数据质量控制研究。

图2 改进的层次分析法模型Fig.2 Improved analytic hierarchy process model

3 基于改进的层次分析法的4G地学空间集成数据质量控制

4G地学空间数据由于其具有多源性、多维性、多属性、异构性以及分布性等特点，其数据集成后的质量问题十分重要，利用改进的层次分析法进行集成数据质量评价，对数据集成具有重要实用价值［7，8］。实施过程中，针对4G地学现象或过程确定指标因素，根据各指标的隶属关系划分若干层次，根据改进的层次分析法的步骤进行计算，利用专家打分的方法，对各层次各要素的相对重要性给出定量指标，然后综合不同专家的意见计算不同层次不同要素的重要性权值，进行综合性评价得出评价结果。

3.1 建立评价指标体系

对4G地学空间集成数据实施质量控制首先要对集成数据进行质量评价。对4G地学空间集成数据质量评价时，要考虑影响数据质量的多种因素。评价数据质量的指标通常包括数学精度、图形数据缺陷、数据属性和数据合法性等。对4G地学空间集成数据进行质量评价时，根据数据特点选用影响数据质量的数学精度、数据属性和数据合法性等几种主要指标构造层次分析模型［9］。

依据层次分析法的原则，4G地学空间集成数据质量评价的指标体系分为目标层、指标层和方案层。目标层是4G地学空间集成数据质量评价，指标层包括数学精度、数据属性和数据合法性等指标，方案层包含不同的决策方案。构建的指标体系如图3所示。

其中数学精度指标的方案层因素包括粗差检测和图形数据缺陷检测两个指标因素;数据属性指标的方案层因素包括一致性检测、重复性检测和关联性检测3个指标因素;数据合法性指标的方案层因素包括与数据标准是否一致检测、数据空间逻辑性检测、高程的合法性检测。拓扑的合法性检测4个指标因素。评价体系建立后，质量控制问题就变为是否把有质量问题的数据放进数据仓库中。

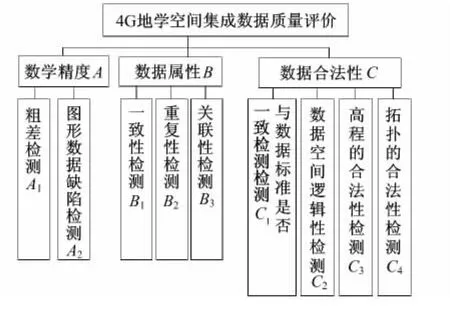
图3 4G地学空间集成数据质量控制指标体系图Fig.3 The control quality indexes system of 4G geological spatial integrated data

3.2 构造判决矩阵并进行一致性判决

将每层中的隶属于同一上层指标的所有要素两两比较，按照表1中的“1～9”的标度对各指标进行主观评定，得到一致性判决矩阵A'=(aij)n×n。

对数据质量控制的各指标标度进行对比评价得到一致性判决矩阵

经计算可得各矩阵的最大特征值

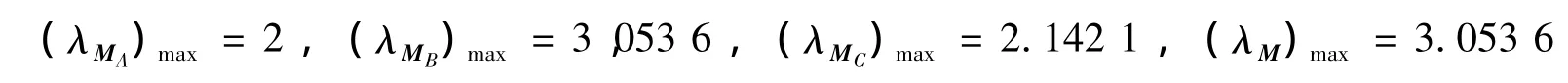
之后进行一致性检验，主要检验一致性矩阵的一致性程度。定义为一致性指标，C越I小，则表示比较所得指标赋值与真实值间一致性程度越高。矩阵的一致性与矩阵阶数有关。定义平均随机一致性指标一致性检验指标当C＜0.1时，认为判决矩阵可以接受，即通过R比较所得赋值是可接受的;否则，应对赋值做相应修正。

分别对4个判决矩阵MA，MB，MC，M进行100次模拟，根据定义的公式进行计算，可得

对于矩阵MA，CI=0.154 7，CI=1.552 1，CR=0.099 7＜0.1，可接受;

对于矩阵MB，CI=0.149 7，RI=1.567 2，CR=0.095 52＜0.1，可接受;

对于矩阵MC，CI=0.154 7，RI=1.552 1，CR=0.099 7＜0.1，可接受;

对于矩阵M，CI=0.149 8，RI=1.567 2，CR=0.095 58＜0.1，可接受。

4个矩阵都满足一致性检验条件，判决矩阵可接受，即赋值结果满足要求［10，11］。

因为层次分析法在构造判决矩阵时采用人工比较赋值的方法，属于定性分析，主观性较强。为了减小主观因素对结果的影响，对应用“1～9”的标度对各指标进行主观评定的方法加以改进，在主观赋值的基础上，引入客观赋值法。客观赋值法是一种加权平均法，操作步骤为设有n个专家为指标权重赋值，m个指标的主观赋值权重为xij，则将同一上层指标对应的两因素间的相关系数定义为［12］

相关权重为

第l个指标的权重为

利用式(1)～式(3)对指标矩阵进行处理，并进行一致性检验，得到改进的赋值法所得的指标矩阵满足一致性要求。

3.3 综合权重计算及一致性检验

综合权重是隶属于同一指标的因素权重相与得到的结果。设k-1准则层权重向量，其中wk-li为k-1准则层指标i在准则层中所占的相对权重。又设第k个准则层指标的各个指标权重

则在准则i下指标j的综合权重

由计算可得指标层各指标综合权重矩阵

3.4 综合评价

假设有m位专家为n个指标打分。设定每个指标可赋值范围为［0，10］，可得主观的量化打分矩阵［12］

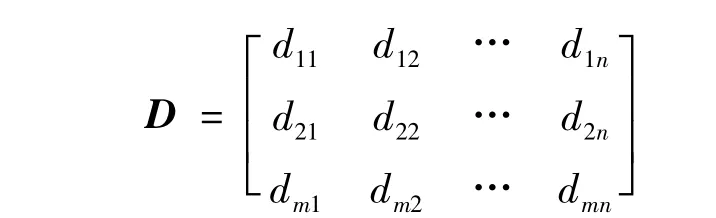
利用求和平均进一步量化得评价数分向量［12］

应用灰度理论得出综合得分值与数据质量的关系如表2所示。

选定3名专家根据检测结果给指标层3个指标评分，得到评分矩阵经平均求和量化后得评分向量

表2 综合得分值与数据质量对应关系表Tab.2 Corresponding score and data quality

对照得分与质量关系表可以看出，4G地学空间集成数据综合质量为好。

分别用典型应用层次法和改进的层次分析法对数据质量进行10次综合评价。应用典型层次分析法对数据质量评价得出的结果矩阵为［6.1，7.3，8.6，9.2，9.6，5.5，3.1，7.4，8.1，8.5］，均方根误差为1.91。应用改进的层次分析法对数据质量评价得出的结果矩阵为［8.2，8.4，8.3，8.5，8.0，7.9，8.3，8.3，8.2，8.1］，均方根误差为0.79，分析误差降低约59%。对比可得，采用改进的层次分析法可有效降低主观因素的影响，提高数据质量评价的客观性。

4 结 语

计算得出的结论符合实际规律。数学精度对数据质量影响最大，粗差检测和图形数据缺陷检测这些数据质量问题来自于数据源，数据源误差是数据质量问题的主要来源。应用改进的层次分析法能对数据质量作出合理的定量评价，能更加真实客观地反映集成数据的质量状况，为提高数据质量、加强数据质量控制提供数学定量参考。

［1］路来君，韩冰.地学G4I系统中数据集成技术研究［D］.长春:吉林大学地球科学学院，2011:137-145.LU Laijun，HAN Bing.Research on the Data Integration of G4I System［D］.Changchun:College of Earth Sciences，Jilin University，2011:137-145.

［2］SAATY T L.Decision-Making with the AHP:Why is the Principal Eigenvector Necessary［J］.European Journal of Operational Research，2003，145(21):85-91.

［3］ZHANG Jie，TANG Hong，SU Kai.Research on Methods of Effectiveness Evaluation［M］.Beijing:Defense Industry Press，2009.

［4］杨澎，初禹，杨湘奎，等.层次分析法(AHP)在三江平原地质环境质量评价中的应用［J］.地质通报，2005，24(5):485-490.YANG Peng，CHU Yu，YANG Xiangkui，et al.Application of the Analytic Hierarchy Process(AHP)in the Sanjiang Plain Geological Environment Quality Evaluation ［J］.Geological Bulletin of China，2005，24(5):485-490.

［5］韩超，泮晓华，李国梁，等.基于GIS多源信息集成的含水层富水性模糊层次分析法［J］.水文地质工程地质，2012，39(4):19-25.HAN Chao，PAN Xiaohua，LI Guoliang，et al.The Fuzzy AHP on Watery of Multi-Source Information Integration Aquifer Based on GIS System［J］.Hydrogeology＆ Engineering Geology，2012，39(4):19-25.

［6］邓吉秋，鲍光淑，刘斌.基于GIS的层次分析法的应用［J］.中南工业大学学报，2002，34(2):1-4.DENG Jiqiu，BAO Guangshu，LIU Bin.Application of the Analytic Hierarchy Process(AHP)Based on GIS［J］.Journal of Central South University，2002，34(2):1-4.

［7］韩李涛，赵军.空间数据质量相关问题探讨［J］.东北测绘，2003，26(1):11-14.HAN Litao，ZHAO Jun.Research on Related Technologies of Space Data Quality ［J］.Northeast Surveying and Mapping，2003，26(1):11-14.

［8］杨秀梅.地质空间数据质量问题探讨［J］.地矿测绘，2010，26(2):33-37.YANG Xiumei.Study on the Geological Spatial Data Quality ［J］.Surveying and Mapping for Geologic Research and Rain-Real Prospecting，2010，26(2):33-37.

［9］陈为公，陈为标，蔡洪春.基于MAPGIS的地学空间数据库中数据质量的研究［J］.地质与资源，2002，11(4):233-235.CHEN Weigong，CHEN Weibiao，CAI Hongchun.Research on Data Quality of Geological Spatial Database Based on MapGIS［J］.Geology and Resources，2002，11(4):233-235.

［10］刘威，路来君，王洪肖，等.基于G4ICSS系统的数据挖掘并行算法［J］.吉林大学学报:信息科学版，2013，31(3):324-327.LIU Wei，LU Laijun，WANG Hongxiao，et al.Parallel Algorithm of Data Mining Based on G4ICSS System ［J］.Journal of Jilin University:Information Science Edition，2013，31(3):324-327.

［11］曾衍伟，龚健雅.空间数据质量控制与评价方法及实现技术［J］.武汉大学学报，2004，29(8):686-690.ZENG Yanwei，GONG Jianya.Spatial Data Quality Control and Evaluation Method and Realization Technology［J］.Journal of Wuhan University，2004，29(8):686-690.

［12］HE Bin，ZHAO Hongzhou，YU Saifa.Research on Evaluation Electromagnetic Environment Effects of Tactical Communications Training Based on AHP［C］∥Proceedings of the Third Electromagnetic Environment Effects and Protection Technology Symposium.［S.l.］:Scientific Research Publishing，2012:245-246.