瞬态曲线分段线性化方法研究及其程序实现

施 杨 祖洪彪

（上海核工程研究设计院 上海 200233）

瞬态曲线分段线性化方法研究及其程序实现

施 杨 祖洪彪

（上海核工程研究设计院 上海 200233）

核电厂的瞬态数据是相关设备应力分析和评定的必要输入。然而，电厂实际运行记录数据或设计瞬态计算数据通常由时间间隔很短的大量数据点构成，直接作为应力分析的输入将会导致大量不必要的计算。为了简化分析，一般需要将瞬态数据曲线进行分段线性化处理。本文基于最小二乘法，开发了一种瞬态曲线分段线性化的方法，并且通过编写PLTC (Piecewise Linearization for Transient Curves)程序予以实现。分别采用标准正弦函数曲线和核电厂典型瞬态曲线对本文的方法进行了验证，结果表明，本文的方法和程序能够很好地实现瞬态曲线的分段线性化。本文的研究有助于提高核电厂瞬态曲线分段线性化的效率和精度。

瞬态，分段线性化，最小二乘法，程序

根据ASME锅炉及压力容器规范第III卷的相关要求，核电厂反应堆冷却剂系统的核安全一级设备需进行疲劳分析。瞬态曲线（温度、压力等物理量随时间的变化曲线）是疲劳分析所必需的输入数据。然而，每一条瞬态曲线往往都包含成千上万个数据点。为了简化计算，一般需要对瞬态曲线作分段线性化处理，即用分段直线代替原始的由成千上万个数据点组成的曲线。在此之前，这部分工作主要通过人工手动完成，耗费了大量的人力。

最小二乘法拟合是一种应用非常广泛的数据分析方法，其基本思想是：按照残差平方和最小的原则，寻找数据的拟合函数关系式。最小二乘法拟合的绝大部分应用都是针对所有需要分析的数据，计算得到与之符合较好的统一的函数关系式。实测数据或曲线的拟合结果往往是高次多项式，高次项将带来复杂的计算，不便于应用。分段拟合可以有效降低拟合函数的阶次。然而，采用最小二乘法将数据或曲线分段拟合的研究工作相对较少。赵明富等[1]将热电势-温度关系曲线分段拟合为二次函数。韩庆瑶等[2]将空间离散点进行了分段直线拟合。谢友宝[3]对曲线进行了分段直线拟合，通过直线倾斜角的变化确定分段点。这种分段方法的缺陷是：在拟合过程中不能很好地控制残差，需要增加外部循环来得到满足精度要求的分段拟合直线。

本文基于最小二乘法，开发一种瞬态曲线分段线性化的方法，通过计算机编程予以实现。本文的研究将使核电厂瞬态数据曲线分段线性化的工作从人工完成转变为程序实现，从而节省人力成本，同时可避免人工操作引入的误差。

1 最小二乘法分段线性化

1.1 基本思想

本文对瞬态曲线进行分段线性化处理的基本思想是：从瞬态曲线的第一个数据点出发，作经过该点的直线。直线斜率不同，所有被拟合点与直线之间误差的平方和也不同，因此可以采用最小二乘法来确定拟合直线的斜率。另外，被拟合的数据点越多，误差也就越大。从两个数据点的拟合（即连线）开始，逐渐增加点数，直到误差超过限值，即完成当前曲线段的线性拟合。之后，从前一曲线段的最后一个数据点出发，开始下一段曲线的线性化处理。

具体步骤如下：

(1) 对于需要处理的n个数据点(t1, f1)、(t2, f2)、……、(tn, fn)，首先给定一个误差限值ε。

（2） 取起始2个点(t1, f1)和(t2, f2)，采用最小二乘法计算经过点(t1, f1)的拟合直线(初始时即两点连线)。加入第3个点(t3, f3)，采用最小二乘法重新计算经过点(t1, f1)的拟合直线。若这三个点与直线对应纵坐标的最大误差emax≤ε，则将(t3, f3)包含在拟合直线中。继续加入第3、第4……第p个点，直到加入第p+1个点时对应的emax>ε，第一条拟合直线L1得以确定（即为前p个点的拟合直线）。

(3) 以点(tp, fp)为起始点，重复第(2)步的过程，计算经过点(tp, fp)的第二条拟合直线。

(4) 重复上述过程，直到处理完所有n个数据点，得到全部拟合直线L1、L2、……、Lm。

(5) 对相邻两条直线的过渡时刻进行处理。例如，直线L1、L2的过渡时刻为tp，这一时刻对应的物理量f存在两个值1Lf和2Lf。

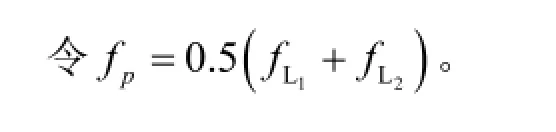
1.2 计算方法

本文采用最小二乘法，确定经过某一固定点的拟合直线的斜率。本节以经过点(t1, f1)的直线L1的斜率的确定过程为例，对具体计算方法进行介绍。

经过点(t1, f1)的直线方程为：

点(ti, fi)对应的残差平方为：

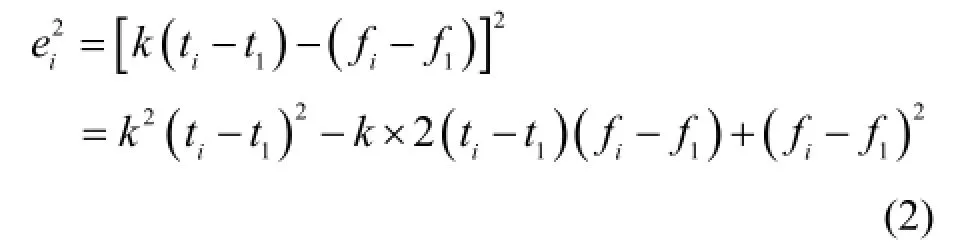
于是，所有p个点的残差平方和为斜率k的函数：

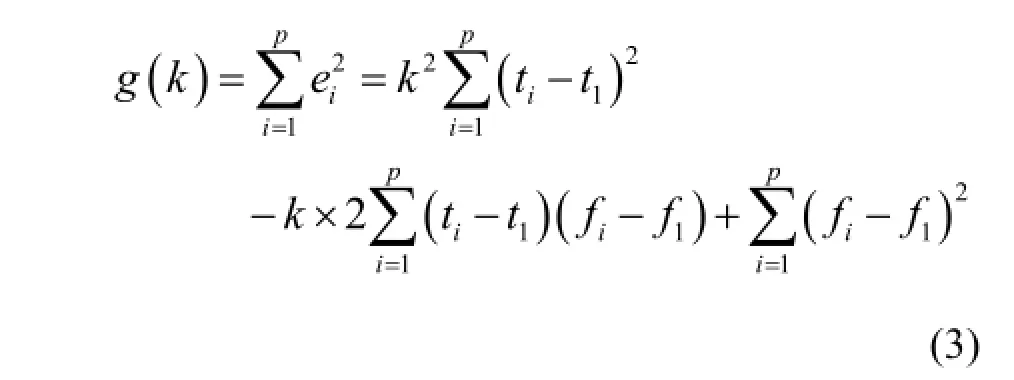
令

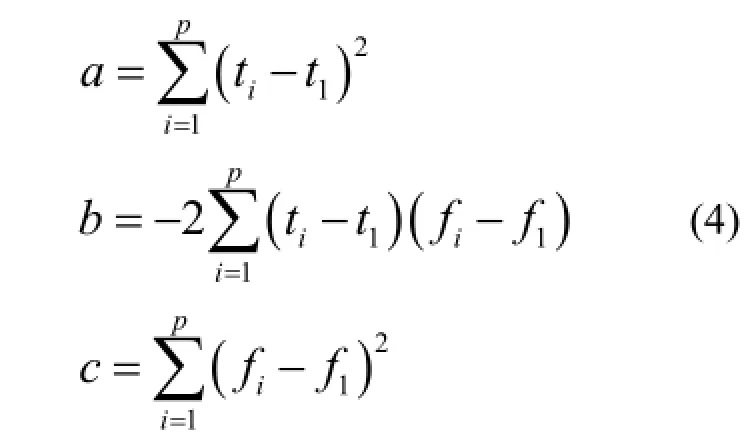
则

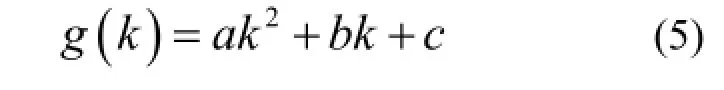
于是

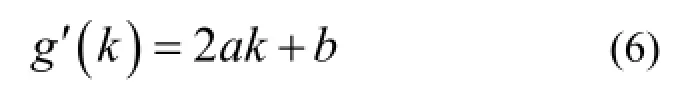
当g(k)取得最小值时，必定有g'(k)=0，解得

可见，对于点(t1, f1)-(tp, fp)，只需要通过式(4)计算a和b的值，并代入式(7)计算拟合直线的斜率k。最后通过式(1)即可得到拟合直线的表达式。

1.3 程序实现

本文根据上述方法和步骤编写了PLTC程序，程序流程如图1所示。

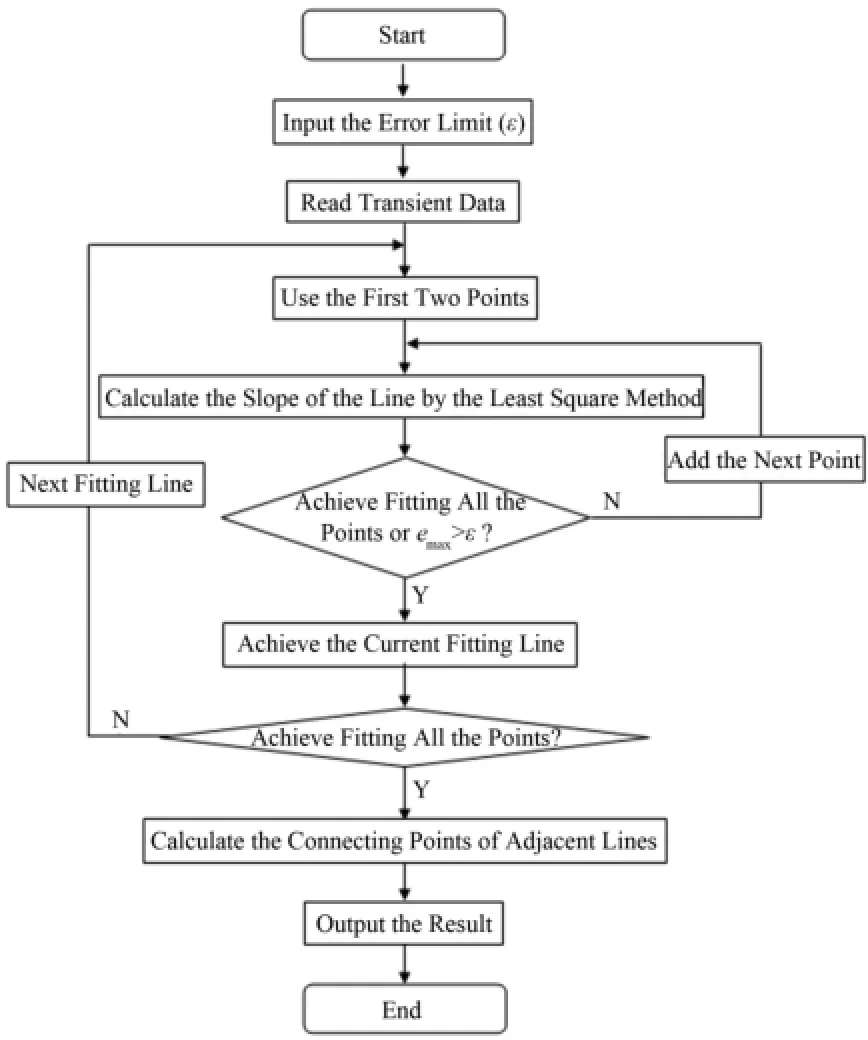
图1 PLTC程序流程图Fig.1 Flow chart of the PLTC program.

1.4 误差分析

本文在对瞬态曲线进行分段线性化处理的过程中引入了一些误差，主要包括：采用最小二乘法进行分段线性拟合的误差；将分段直线进行连接所引入的误差。

第一部分误差在计算中进行了严格控制

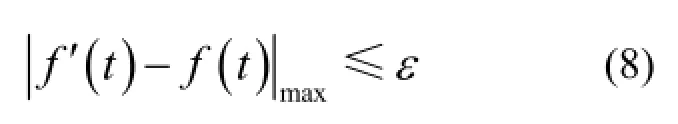
式中，f(t)为原始瞬态曲线；f '(t)为进行连接处理前的分段线性化结果；ε为人为设定的误差限值。

第二部分误差如图2所示。图中实线为进行连接处理前的分段拟合直线，虚线为做了连接处理后的最终分段线性化结果。点A-D表示瞬态曲线上的原始数据点，点B'和C'为拟合直线段的末尾端点，B"和C"为连接点，且有

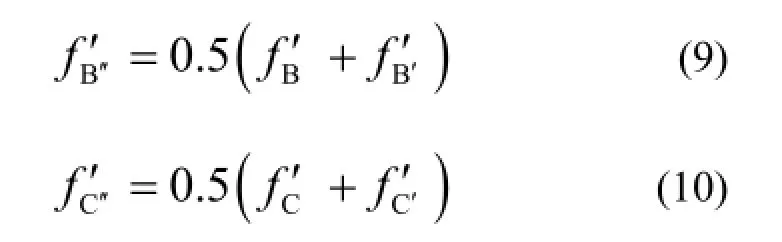
由式(8)可知：

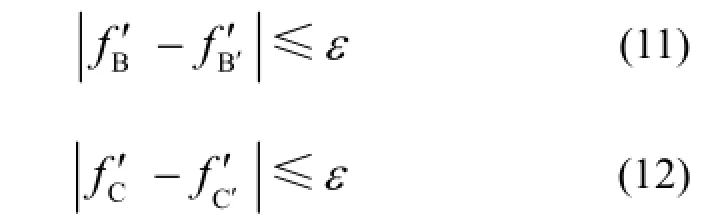
于是有

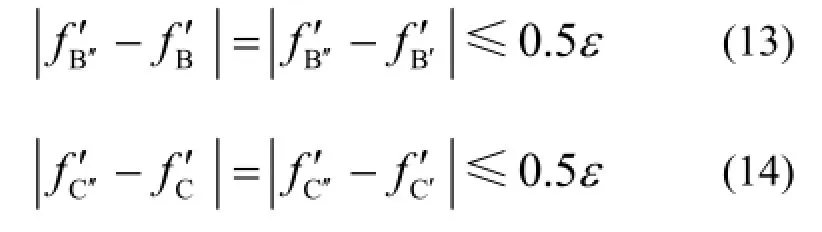
不失一般性，对拟合直线BC'变换为B"C"的过程进行分析。主要存在两种情况：如图2(a)所示，BC'与B"C"不相交，则连接处理的误差范围为如图2(b)所示，BC'和 B"C"相交，在这种情况下，连接处理的误差范围为由式(13)和(14)可知，无论上述哪种情况，这部分误差均不超过0.5ε。

整体误差不超过上述两部分误差之和，即1.5ε。可见，只要给定ε值，整体误差就是可控的，因此不需要增加外部循环来控制整体误差。

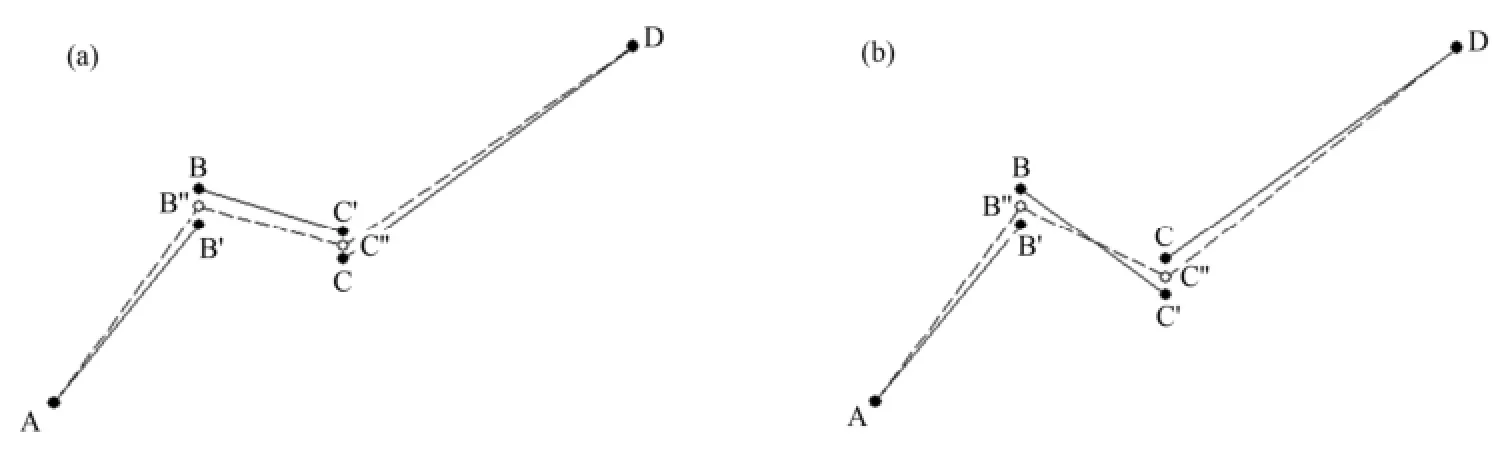
图2 分段直线连接处理示意图Fig.2 Structure of piecewise lines.

2 应用实例

本节采用PLTC程序分别对标准正弦函数曲线和核电厂典型瞬态曲线进行分段线性化处理，将处理后的曲线与原始曲线进行比较，验证PLTC程序的正确性。

给定误差限值ε=2(fmax-fmin)/300，即程序整体计算最大误差不超过(fmax-fmin)/100(即1.5ε)。计算结果如图3-5所示，分段线性化结果与原始曲线基本重合。可见，通过PLTC程序可以得到满足计算精度要求的分段线性化的瞬态曲线。在实际应用中，可以根据需要适当降低精度要求，以减少拟合点数。

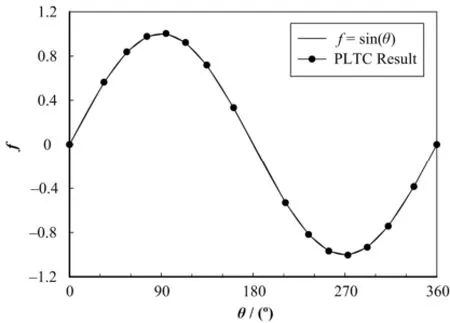
图3 标准正弦函数曲线Fig.3 Standard sine curve.

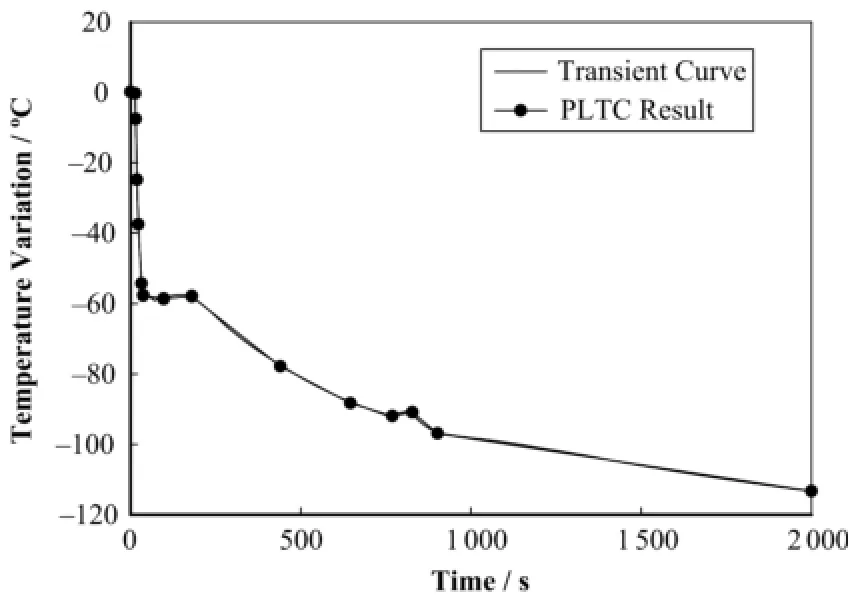
图4 某设计瞬态下温度变化量的时程曲线Fig.4 Time history curve of temperature variation under some design transient.

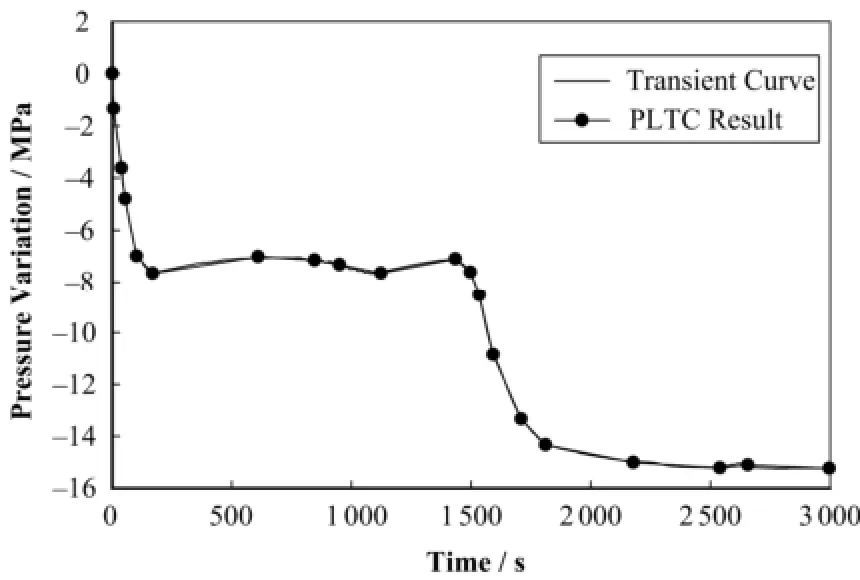
图5 某设计瞬态下压力变化量的时程曲线Fig.5 Time history curve of pressure variation under some design transient.

在以往的核电厂一回路主设备应力分析过程中，瞬态数据曲线分段线性化工作主要通过人工手动完成。首先将核电厂实际记录数据或设计瞬态计算数据画成曲线，之后通过人工取点的方式得到分段线性化结果。人工取点过程有较大的主观性，无法保证精度，而且效率很低，完成一个设备应力分析和评定所需的瞬态数据分段线性化处理耗时3-4个月。采用本文的PLTC程序，则可快速完成瞬态数据曲线的分段线性化工作，可节约70%的时间成本，同时精度也可以得到保证。

3 结语

本文基于最小二乘法，开发了一种计算简单，易于编程实现的瞬态曲线分段线性化方法。基于该方法编写了PLTC程序，并通过标准正弦函数曲线和核电厂典型瞬态曲线对本文的方法进行了验证。结果表明，本文的方法和程序能够很好地实现瞬态曲线的分段线性化。本文的研究将大大节省核电厂瞬态曲线分段线性化工作的人力成本，同时避免人工操作带来的误差。

1 赵明富, 廖强, 钟连超, 等. 热电偶最优化分段最小二乘拟合线性化处理方法[J]. 计量技术, 2004, 1: 18-20

ZHAO Mingfu, LIAO Qiang, ZHONG Lianchao, et al. Thermocouple optimization piecewise least square linearization method[J]. Measurement Technique, 2004, 1: 18-20

2 韩庆瑶, 肖强, 乐英. 空间离散点最小二乘法分段直线拟合的研究[J]. 工业仪表与自动化装置, 2012, 4: 107-109

HAN Qingyao, XIAO Qiang, YUE Ying. Study of space discrete point’s piecewise linear fitting on least square method[J]. Industrial Instrumentation & Automation, 2012, 4: 107-109

3 谢友宝. 最小二乘法分段直线拟合[J]. 南昌航空工业学院学报, 1992, 1: 19-25

XIE Youbao. Sectional line fitting by means of least square method[J]. Journal of Nanchang Institute of Aeronautical Technology, 1992, 1: 19-25

CLCTL364+.2

Study and program implementation of transient curves’ piecewise linearization

SHI Yang ZU Hongbiao
(Shanghai Nuclear Engineering Research & Design Institute, Shanghai 200233, China)

Background: Transient curves are essential for the stress analysis of related equipments in nuclear power plant (NPP). The actually operating data or the design transient data of a NPP usually consist of a large number of data points with very short time intervals. To simplify the analysis, transient curves are generally piecewise linearized in advance. Up to now, the piecewise linearization of transient curves is accomplished manually. Purpose: The aim is to develop a method for the piecewise linearization of transient curves, and to implement it by programming. Methods: First of all, the fitting line of a number of data points was obtained by the least square method. The segment of the fitting line is set while the accumulation error of linearization exceeds the preset limit with the increasing number of points. Then, the linearization of subsequent data points was begun from the last point of the preceding curve segment to get the next segment in the same way, and continue until the final data point involved. Finally, averageing of junction points is taken for the segment connection. Results: A computer program named PLTC (Piecewise Linearization for Transient Curves) was implemented and verified by the linearization of the standard sine curve and typical transient curves of a NPP. Conclusion: The method and the PLTC program can be well used to the piecewise linearization of transient curves, with improving efficiency and precision.

Transient curves, Piecewise linearization, Least square method, Program

TL364+.2

10.11889/j.0253-3219.2014.hjs.37.010604

施杨，男，1984年出生，2012年于浙江大学获博士学位，现从事的专业为反应堆结构力学

2013-11-13，

2013-12-10