渐消记忆自适应滤波在传递对准中的应用

屈新芬，李世玲，曾 超，肖龙远

（中国工程物理研究院电子工程研究所，四川 绵阳621900）

0 引言

传递对准是子捷联惯导系统在舰载、机载、车载武器等动基座下启动正常工作的关键环节，其对准精度直接关系到子惯导系统的导航精度。在传递对准中，最常采用的方法是经典卡尔曼滤波算法，而经典卡尔曼滤波算法对系统模型准确度依赖高，对噪声统计特性已知程度要求高；而实际应用中，系统噪声统计特性经常发生变化，滤波状态方程建模与实际模型往往存在一定差异，状态量可能存在突变等，都将导致卡尔曼滤波器性能下降，甚至发散［1］。

为解决这一问题，出现了许多种自适应卡尔曼滤波和鲁棒滤波在传递对准中应用的研究，主要包括Sage-Huge自适应滤波算法，模糊自适应卡尔曼滤波算法，神经网络自适应卡尔曼滤波算法，衰减记忆卡尔曼滤波算法和H∞滤波算法等。Sage-Husa自适应滤波［2］是次优无偏极大后验估计，噪声统计特性由滤波时在线估计；该方法需要保证量测噪声协方差阵的正定性和系统噪声协方差阵的半正定性，否则容易产生滤波发散，且计算量较大。模糊自适应卡尔曼滤波［3］将模糊逻辑方法与卡尔曼滤波相结合，由设计的模糊推理系统在线实时调整系统和量测噪声方差，防止滤波器发散；然而该方法需要对机动环境进行一定的事先了解，需要根据机动环境的噪声特性对隶属度函数做适当的调整。神经网络自适应卡尔曼滤波算法［4］利用神经网络在线对测量噪声进行估计和自适应调节，提高了对失准角估计的精度，然而神经网络使用前需要进行大量的训练，工作量较大。文献［5-6］提出了衰减记忆滤波算法，利用衰减因子限制卡尔曼滤波器的记忆长度，增加了当前量测信息的利用权重，降低了对验前信息的依赖性；该方法中给定的单纯衰减因子常数不能准确地调整所有的状态。文献［7-11］中提出的衰减因子自适应估计的计算量较大。H∞滤波算法［12］中Riccati方程的计算量大且复杂，影响了传递对准的快速性。

针对此，本文将渐消记忆自适应滤波算法用于传递对准中，根据实时计算的新息计算渐消因子，并将计算的渐消因子加入滤波中，构成次优滤波以抑制系统滤波的发散，从而保证捷联惯性子系统动基座传递对准的精度。

1 渐消记忆自适应滤波

设系统的状态方程和量测方程分别为：

其中，Xk为k时刻的n维状态矢量，Zk为k时刻的m维观测矢量，Fk／k-1为k-1到k时刻的一步转移矩阵，wk-1为k-1时刻的系统噪声，Gk-1为系统噪声矩阵，Hk为k时刻的观测矩阵，vk为k时刻的m 维观测噪声，系统噪声和观测噪声的方差阵分别为Qk和Rk，初始状态的统计特性为E［X0］=mX0，Var［X0］=P0，X0、wk-1和vk三者互不相关。

该系统对应的渐消记忆自适应滤波公式表达式如下［13-15］：

基本卡尔曼滤波的最优增益阵Kk只按噪声的验前信息计算，如果验前信息不准确则可能引起滤波发散。采用渐消记忆因子自适应滤波算法，除了验前信息以外，还通过渐消因子sk，利用量测数据，在每次计算中，保证对Kk进行必要的修正。当估计误差不断增大时，新息rk／k-1增大，导致rk／k-1rTk／k-1增大，使sk增大，从而使Pk／k-1增大，Kk的范数也增大。由此测量值就具有较大的加权系数。

2 速度加积分角速度匹配的滤波器模型

2.1 系统方程的建立

“速度+积分角速度”匹配的传递对准误差模型主要由捷联惯导系统的速度误差方程、姿态误差方程、惯性器件误差方程以及积分角速度误差方程组成［1］。

其中，速度误差方程为：

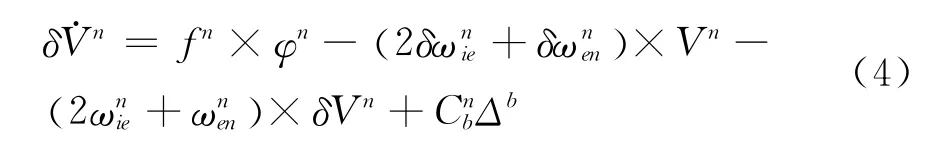
姿态误差方程为：

惯性器件误差方程取为：

积分角速度误差方程取为：

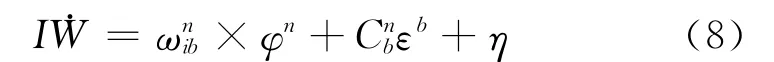
式（4）—式（8）中：φn为计算的子惯导平台失准角；ωnin是由子惯导计算得到的导航系相对惯性系的角速度在导航系中的投影；ωnib为子惯导检测的运载体旋转角速度在导航坐标系的投影。δωnin是ωnin的误差；δVn是子惯导测量的速度误差；fn是子惯导的比力在导航系上的投影；Cnb是子惯导载体系相对导航系的姿态矩阵；ωnie是子惯导测得的地球自转角速率在导航系上的投影；ωnen是子惯导导航系相对地球坐标系的角速率在导航系中的投影；δωnie是ωnie的误差；δωnen是ωnen的误差；εb和Δb分别为子惯导在载体坐标系下的陀螺常值漂移和加表常值偏置；IW 为积分角速度误差向量；η为白噪声。

根据式（4）-（8）可建立滤波器状态方程为：

其中，取：

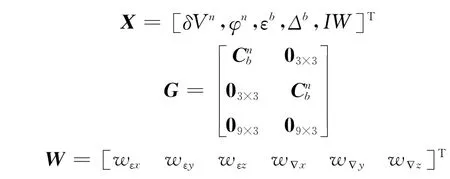
X 为状态变量，F 为状态转移矩阵；G 为系统噪声转移矩阵，W 为系统噪声矢量，并假设其为零均值高斯白噪声。

2.2量测方程的建立

本系统采用“速度+积分角速度”匹配方式进行动基座传递对准。积分角速度匹配方法不仅继承了角速度匹配对运载体角运动敏感的特点，而且通过积分处理可以有效地衰减角速度中的高频噪声。因此“速度+积分角速度”匹配方式具有减小运载体振动和挠曲变形对系统精度的不利影响，提高对准精度的优点。

下面给出详细的推导，来说明速度和积分角速度传递对准的原理。

定义积分角速度的表达式为：

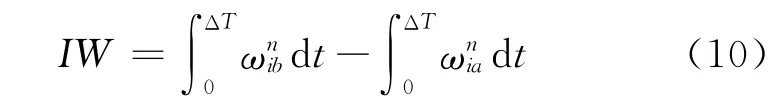
其中ΔT 为积分周期，ωnib为子惯导检测的运载体旋转角速度在导航坐标系的投影，ωnia为主惯导检测的运载体旋转角速度在导航坐标系的投影。对式（10）求导可得：

增加状态变量IW，则积分角速度匹配观测方程为：

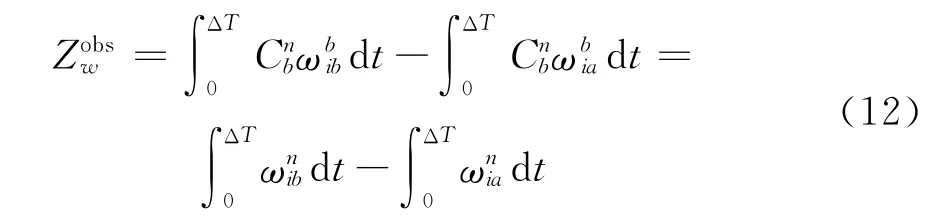
而积分角速度匹配量测方程为：

速度匹配的观测方程：

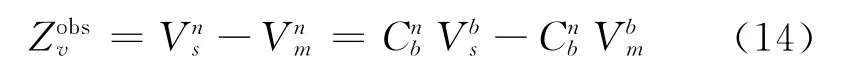
而速度匹配量测方程为：

取主子惯导的速度差和积分角速度差作为量测变量，完整的量测方程为：

其中：

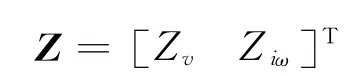
3 仿真结果

3.1 仿真条件

为了验证主子惯导空中传递对准系统性能，设计了一组飞行轨迹。设飞机的初始位置为：北纬32.05°，东经118.766 7°，高度0m；飞机的初始速度为0m／s，航向135°，姿态角为0°。采用的子惯导陀螺全温范围的常值漂移为10（°）／h，加速度计零偏为5mg。飞行任务有上升、加速、下降、左拐、右拐、平飞等，飞行时间为150s。

在噪声不确切的情况下，程序中的X0、P0、Q0、R0仿真初始条件给定如下：

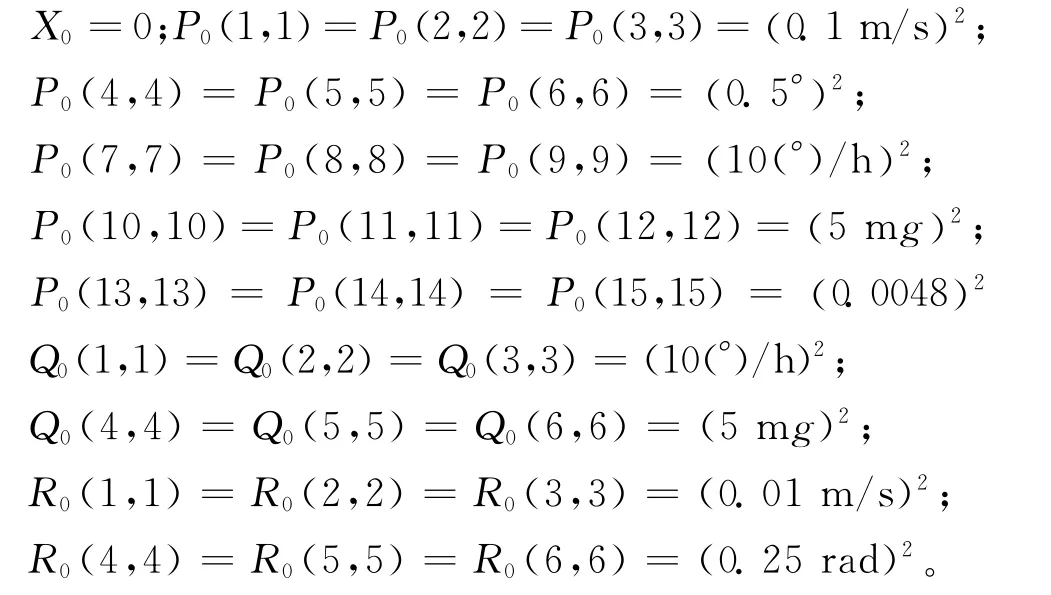
3.2 仿真结果

实际滤波中取R=8R0（模拟噪声统计不准确的情况），分别采用常规卡尔曼滤波和渐消记忆自适应滤波对子捷联惯导系统误差进行估计，结果如图1、图2和图3所示。

图1、图2和图3中实线表示采用常规卡尔曼滤波算法计算得到的X 轴、Y 轴和Z 轴的失准角估计误差曲线，虚线表示采用渐消记忆自适应滤波算法计算得到的失准角估计误差曲线。由此可见，渐消记忆自适应滤波计算得到的X 轴、Y 轴和Z 轴的失准角估计误差在10s时都收敛到10′以内，最终分别收敛到3′、0.5′和0.6′以内；而采用常规卡尔曼滤波计算得到的X 轴、Y 轴和Z 轴失准角估计误差分别在38s、35s和40s时才能收敛到10′以内，最终分别收敛到4′、0.6′和2′以内。

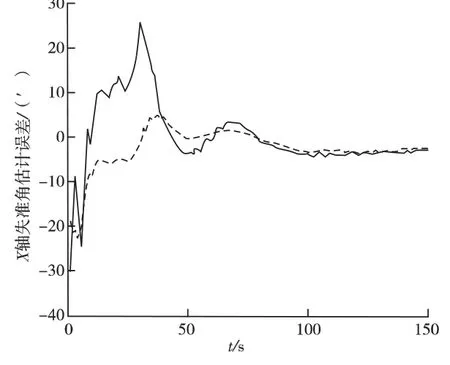
图1 X 轴失准角估计误差曲线Fig.1 X-axis misalign angle estimation error curve

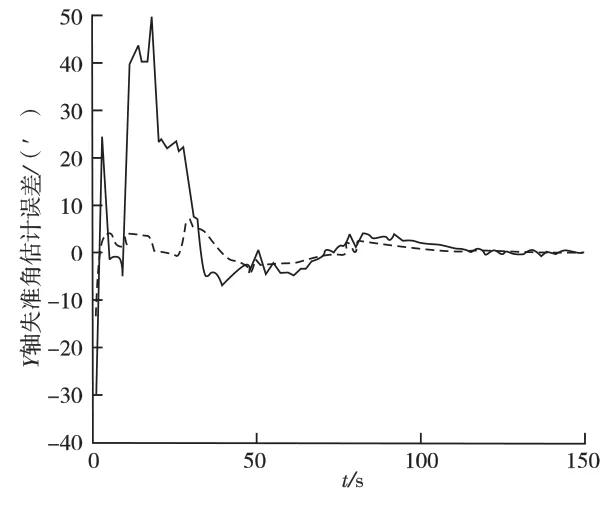
图2 Y 轴失准角估计误差曲线Fig.2 Y-axis misalign angle estimation error curve

图3 Z 轴失准角估计误差曲线Fig.3 Z-axis misalign angle estimation error curve

通过对上述失准角估计误差曲线的比较，可以看出在噪声统计不准确的情况下，渐消记忆自适应滤波算法收敛速度较经典卡尔曼滤波更快，精度更高，同时系统的健壮性与稳定性也得到了提高。

4 结论

本文将渐消记忆自适应滤波算法用于传递对准中，该方法引入新息计算渐消因子，并将该渐消因子加入滤波中，调节了滤波的性能，抑制了系统模型存在误差和量测信息突变下滤波的发散性。利用设计的对挠曲效应有抑制作用的“速度+积分角速度”匹配模式进行仿真，仿真结果表明，在噪声不确定的情况下，渐消记忆自适应滤波算法能有效地提高对准精度和缩短对准时间。

［1］付梦印，邓志红，张继伟.Kalman滤波理论及其在导航系统中的应用［M］.北京：科学出版社，2003：4-6.

［2］刘广军，郭晶.次优Sage滤波器的改进措施［J］.火力与指挥控制，2003，28（1）：78-81.

［3］徐田来，游文虎，崔平远.基于模糊自适应滤波的INS／GPS组合导航系统算法研究［J］.宇航学报，2005，26（5）：571-575.

［4］赵剡，王纪南，解春明.基于联邦网络的传递对准滤波补偿 算 法［J］.北 京 理 工 大 学 学 报，2012，32（10）：1077-1081.

［5］Fagin S L.Recursive linear regression theory，optimal filter the-ory and error analysis of optimal systems［J］.IEEE Convention Record，1964，12：216-240.

［6］Sorenson H W，Sacks J E.Recursive fading memory fil-tering［J］.InformationSciences，1971，3（2）：101-11

［7］徐景硕，秦永元，彭蓉.自适应卡尔曼滤波器渐消因子选取方法研究［J］.系统工程与电子技术，2004，26（11）：1552-1554.

［8］Xia Q J，Rao M，Ying Y Q，et al.Adaptive fading Kalman filter with an application［J］.Automatica，1994，30（12）：1333-1338.

［9］Levent O，Aliev F.A comment on adaptive fading Kalman filter with an application［J］.Automatica，1998，34（12）：1663-1664.

［10］耿建睿，崔中兴，张洪钺，等.衰减因子自适应滤波及在组合导航中的应用［J］.北京航空航天大学学报，2004，30（5）：434-437.

［11］高青伟，赵国荣，吴芳，等.衰减记忆自适应滤波在惯导系统传递对准中的应用［J］.系统工程与电子技术，2010，32（12）：2648-2651.

［12］宋丽君，秦永元，严恭敏.H∞次优滤波在速度姿态匹配传递对准中的应用［J］.传感技术学报，2012，25（1）：49-52.

［13］Gao Fuquan，Ding Chuanhong，Liu Jianfeng.Initial alignment of strapdown inertial navigation system using Kalman filter［C］／／International Conference on Computer Application and System Modeling.Taiyuan，China，2010：629-633.

［14］Ma Yunfeng.Application of fault tolerant and federated strong tracking Kalman algorithm in integrated navigation system［C］／／IEEE Conference on Consumer Electronics，Communications and Networks.XianNing，China，2011：3946-3949

［15］Gao Weixi，Miao Lingjuan，Ni Maolin.Multiple fading factors kalman filter for SINS static alignment application［J］.Chinese Journal of Aeronautics，2011，24：476-483.