基于相位估计与补偿的时域同步平均方法

陈韶华，邓秀华，张 恒

（中船重工集团公司第七一〇研究所，湖北 宜昌443003）

0 引言

时域平均使信号同相位平均，而噪声相位是随机的，因而能增强噪声中的周期信号，在微弱信号检测、振动测试与故障诊断等领域有广泛应用［1-5］。时域同步平均要求分段数据长度等于信号周期的整数倍，这在信号频率未知时难以做到。即使频率已知，由于数字信号处理中离散采样的原因，各段信号之间也可能存在相位差，不能完全同步。为解决分段数据相位不同步的问题，一般采用在频率轴上搜索的方法。文献［4］针对信号频率范围已知的情况，在该范围内进行搜索来寻求最佳分段长度及最大增益。文献［5］在分段长度一定的情况下，在频率轴上搜索以进行相位补偿。这些方法的缺点是需要在频率轴上进行庞大的搜索，处理效率比较低。本文针对此问题提出了基于相位估计与补偿的时域平均方法。

1 时域平均的理论分析

为了便于理论分析，采用复正弦信号形式，数字信号表示为：

其中，ω0=2πf0／fs是归一化角频率，f0与fs分别是信号频率与采样频率，φ是在［0，2π）上均匀分布的随机相位。

在分段平均的情况下，每段数据可定义为：

各段数据之间可部分重叠或不重叠。R ＜N 时部分重叠，R=N 时不重叠。如部分重叠应保证偏移长度R大于噪声的相关半径。这样，对高斯分布噪声，各段之间仍可视为相互独立。

时域平均表示为：

当ω0R为2π的整数倍时，sl（n），l=0，…，L-1各段数据对于信号而言是同步平均的。

考虑到ω0R=2πRf0／fs=2πRTs／T0（其中Ts、T0分别为采样间隔与信号周期），可以看出，只有当平移的样本长度等于信号周期的整数倍时，信号同步平均。

当Rf0／fs不是整数时，分段数据不能够同相位平均。把Rf0／fs表示为一个整数k与一个小数Δ之和。

则式（3）表示为：

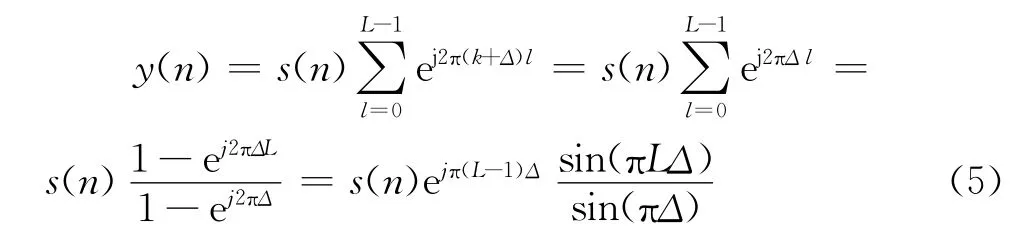
可见，当Δ不为0时，引起时域平均增益的损失。归一化增益表示为：

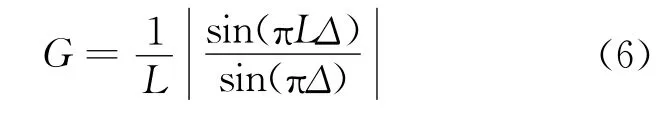
根据式（6）可以画出归一化增益与相位差、平均次数的关系，如图1所示。可见，相位差越大，平均次数越多，增益损失越大。如果能把相位差与平均次数控制在一定范围之内，可以得到较大的处理增益。但是在频率未知的条件下，这很难做到。

2 基于相位补偿的时域平均原理

把式（4）代入式（2），得到

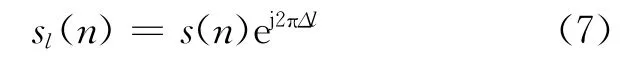
可以看出，在某一个时间序号n上，sl（n），l=0，…，L-1序列是未知量Δ的复正弦函数。对sl（n），l=0，…，L-1做FFT，得到

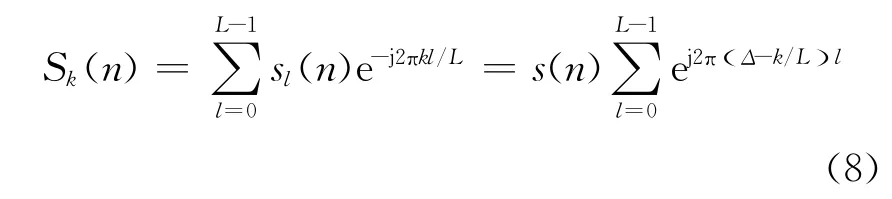
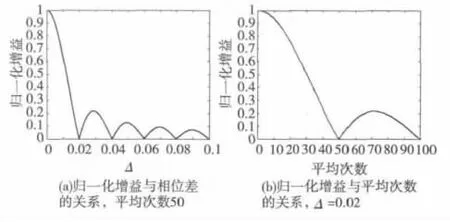
图1 归一化增益与相位差、平均次数的关系Fig.1 Normalized processing gain versus phase difference and averaging times

为了充分利用数据序列的能量，提高低信噪比下相位差估计能力，应该对分段数据矩阵

的每列分别做FFT，幅度平均，再求峰值对应的kmax。为了提高Δ的估计精度，可采用对sl（n）补零以后做FFT的方法［6］，或者对Sk（n）插值。

对式（7）两端乘以e-j2πΔ^l以消除分段信号之间的相位差，得

再进行时域平均，

就实现了对未知频率周期信号分段相位不同步的相位差补偿，达到了同相平均的目的。相位补偿后时域同步平均达到了最大处理增益10lgL。

3 多频率成分的情况

在周期信号中存在多个频率成分时，由于分段引起不同频率在各段之间的相位差一般是不同的，通过第2节方法只能估计较强信号的相位差Δ，相位补偿后时域平均也只能加强该信号。为了解决多个频率成分的问题，我们采用自适应notch滤波器法［7］，进行循环处理。对于每次经过相位补偿和时域平均处理增强后的频率成分，采用自适应notch滤波技术从混合信号中消除该信号，然后重复第2节的处理，直到所有频率成分都增强并提取出来。自适应notch滤波器通过权值的自适应调整，产生一个与频率已知但相位和幅度未知的频率分量完全相同的信号，从而把它消除掉，常用于自适应干扰抵消中。多频率分量周期信号的时域同步平均示意图如图2所示。

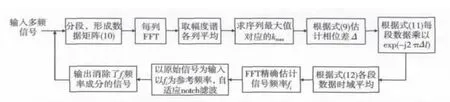
图2 多频率分量周期信号的时域同步平均示意图Fig.2 Sketch map of time averaging with multi-frequency components periodical signal

4 计算机仿真验证

通过计算机仿真验证了没有噪声和低信噪比情况下新方法的性能。

图3 是没有加噪声情况下时域平均处理的结果。信号数字频率0.065，信号长度4 096点，每段长度64点，重叠50%，共分127段。图3（a）是第1段信号，可见信号长度不是其周期的整数倍，直接时域平均仅使幅度增大到原来的2倍，如图3（b）所示，基本上没有起到增强信号的效果。采用本文方法估计相位差并补偿后的时域同步平均结果如图3（c）所示，可见使信号增大了127倍，增益与分段长度一致，达到了最大增益。

图3 单频率周期信号的时域平均处理结果，无噪声Fig.3 Time averaging result of single frequency periodical signal，without additive noise

图4是低信噪比情况下时域同步平均增强微弱周期信号的结果，以2个频率分量为例分析了新方法对多频率分量周期信号的增强和检测效果，信噪比-25dB。信号数字频率分别为0.013和0.026，信号长度15 000点，每段长度256点，重叠50%，共分116段。在-25dB的低信噪比下，从时域波形已完全看不到信号，因此从频域上来观察。图4（a）第1段信号的频谱，由于信号太弱观测不到信号。图4（b）是采用新方法估计并补偿相位差后时域同步平均增强的第1个频率分量的频谱，信号得到增强后有足够的信噪比来估计频率，为0.013。采用自适应notch滤波器消除频率为0.013的频率分量后，对剩余信号继续估计并补偿相位差后同步平均，得到第2个频率分量，如图4（c）所示。图4（d）给出了根据第一次时域同步平均后获得频率分量设计的自适应notch滤波器，滤波器传递函数在信号频率上有一个很深的凹口，原始输入信号通过自适应notch滤波后，消除了第1个频率分量信号，只剩第2个频率分量信号。图4（e）是分段后未补偿相位直接时域平均后信号的频谱，看不到信号。仿真结果表明新方法处理多频率分量周期信号也是有效的。

图4 多频率周期信号的时域平均处理结果，-25dBFig.4 Time averaging result of multi-frequency periodical signal，-25dB

5 结论

本文提出了一种基于分段数据相位差的估计与补偿的时域同步平均方法。该方法采用FFT 估计分段信号相邻段之间的相位差并补偿，使分段信号同步平均以提高信噪比。理论分析和计算机仿真表明，该方法能克服分段长度不等于信号周期整数倍引起的平均效果急剧下降的问题，可以取得最大平均增益，且计算效率远远高于基于频率搜索的传统方法。但该方法在处理多频率分量周期信号时比较复杂，拟进一步改进。

［1］相敬林，王海燕.微弱信号检测技术与近感系统［M］.西安：西北工业大学出版社，1993.

［2］Mcfadden P D.Application of synchronous averaging to vibration monitoring of rolling element bearings［J］.Mechanical Systems and Signal Processing，2000（6）：891-906.

［3］余红英，闫宏伟，潘宏侠.齿轮振动信号分解及其在故障诊断中的应用［J］.振动，测试与诊断，2005，25（2）：109-113.

［4］陈韶华，相敬林.一种改进的时域平均法检测微弱信号研究［J］.探测与控制学报，2003，25（4）：56-59.

［5］陈新华，孙长瑜，鲍习中.基于相位补偿的时域平均方法［J］.应用声学，2011，30（4）：268-274.

［6］胡广书.数字信号处理［M］.北京：清华大学出版社，1997.

［7］惠俊英，蔡平，马晓民.自适应陷波器应用研究［J］.声学学报，1991，16（1）：19-24.