基于模糊层次分析法的滑坡处治方案优化
2014-01-12吴顺川林东华
朱 欣,吴顺川,林东华,肖 术
(1.北京科技大学土木与环境工程学院,北京 100083;2.中色卢安夏铜业有限公司,赞比亚 卢安夏 90456)
0 引言
滑坡处治方案的确定需要考虑多方面因素。施工可操作性、方案的技术可行性、经济因素和安全可靠性等都是需要在滑坡处治方案确定中考虑的因素。这些因素中,一个因素往往是由其他因素所决定的,并且一部分因素只能定性描述,而不能定量描述。因此,滑坡处治方案的选择是定量因素与定性因素相互影响、共同作用下的多目标多层次决策过程。
目前,国内外关于滑坡处治方案的研究较多,但是关于方案优选方面的研究较少。在处治方案优选方面,主要优化方法有层次分析法、模糊熵权法、并行神经网络法、灰色系统法、模糊综合评判法、遗传算法等。但是上述方法应用在方案优选时,大多数方案优选按照决策者的主观倾向和对工程现状的理解能力来确定,这样将使决策结果和实际情况产生较大偏差。因此,在他们的基础上提出了模糊层次分析法,任红岗[1]将此方法运用在分段空场嗣后充填法的采场结构参数优化;李俊芳[2]运用模糊层次分析法对城市轨道交通线网规划方案进行综合评价;何志虎[3]运用模糊层次分析法对泥石流评价方法进行评判;王新民[4]用模糊层次分析法对采矿方法进行选择;张世雄[5]在某工程的爆破方案的选择中也采用了层次分析法;杨晶海[6]运用模糊层次分析法对深基坑工程支护方案进行设计和优选。上述研究主要关注点放在单个方案的优化设计上,综合比较不同方案优劣的方法研究较少,尤其在滑坡处治方案领域应用的可行性还有待研究。
本文以平朔东露天矿东北帮滑坡处治方案优选为工程背景,考虑技术指标、安全稳定指标和经济指标,采用模糊层次分析法构建东露天矿的滑坡处治方案评判体系,再对各种方案指标进行定性和定量评价,并最终给出东露天矿东北帮滑坡灾害处治的最优方案。研究结果对类似的滑坡综合处治方案优选研究具有较大的借鉴意义。
1 模糊层次分析法评价模型
1.1 方案综合评价指标体系构建
方案评价是一个多因素共同作用的过程,只有构建一个科学的、全面的和合理的评价指标体系,评价结果的准确性才有保证。在评价指标体系中,既可能存在定量化指标,又可能存在定性化指标,且这些指标相互影响和制约。以最少的指标,反映最客观的信息是评价指标选取的准绳[2]。利用层次分析法基本原理,可建立方案综合评价(A)指标体系:首先是安全因素(B1),可从处治后的稳定性(X1)等分析;其次是经济指标(B2),可从工程总成本(X2)等分析;最后是技术指标(B3),可从压煤量(X3)、耐久性(X4)、施工工期(X5)、施工难易程度(X6)、方案灵活适应性(X7)、降水 /爆破震动对工程进展的影响(X8)等分析。须指出的一点是,在实际工程的综合评价分析过程中,所使用的指标是有所不同的,应根据具体的工程项目的特点进行选择。
1.2 层次分析法确定权重向量
层次综合评价指标体系结构确定后,各指标在整个体系中的所占比重成为接下来要处理的问题。这里采用层次分析法来解决体系中各因素的权重分配问题。
1.2.1 构造比较标度
将不同方面的因素综合在一个系统中,需要使用相同的评判标准,这样才能体现数据的客观准确性。根据模糊数学的相关理论和优化理论应用的实际经验,选出如下比较标准[7](见表1)作为比较标度。

表1 比较标准意义
1.2.2 构造比较判断矩阵并判断矩阵的一致性检验
在综合评价指标体系的层次结构模型基础上,按照上述的比较标度把每一级指标都与相邻上一级各指标相比较,构造出判断矩阵D,按定义有:

式中:n为相互比较因素的标号。
判断矩阵是由经验决定的,一般受主观因素影响很大。为防止判断矩阵与实际情况存在偏差,进而影响最终结果的准确性,这里要对判断矩阵的特征值λmax进行一致性检验。
对于给定的判断矩阵D=(Xij)nn是否满足一致性要求的过程中,先求出判断矩阵的最大特征值,根据公式(2)、(3)可求得:




根据判断矩阵的阶数,通过查平均随机一致性指标取值表(见表2),可以得到相对应的一致性指标值RI,进而利用一致性检验公式(5)求得CR值。当CR<0.1的时候,认为判断矩阵满足一致性要求,否则,重新调整判断矩阵,直至判断矩阵的一致性可以接受为止。
然后,按式(4)求得一致性检验指标CI:

表2 平均随机一致性指标取值
1.2.3 计算权重向量

1.3 模糊综合评判
1.3.1 隶属矩阵确定
评价系统中常常出现非定量指标和定量指标并存的情况。运用相对二元比较法可以确定非定量指标,而定量指标可以由隶属函数法确定[8]。
a)非定量指标的隶属度通过二元对比的定性排列求得。二元比较矩阵E中的各因子是将目标Xk与Xl作二元对比,若 Xk与 Xl同样重要,则令 ekl=0.5,elk=0.5;若 Xk比 Xl重要,则令 ekl=0,elk=1(k,l=1,2,…,m)。

将相对二元矩阵按行排序,根据排序查语气算子与定量标度表[9](见表3),可得到非定量指标的隶属度。

表3 语气算子与定量标度相对隶属度关系表
b)针对定量指标的隶属函数法是表示对n个方案的m个指标组成的目标特征值矩阵Y按照相应的原则进行规格化,得到定量指标的相对隶属度矩阵R。

式中:i=1,2,…,m;j=1,2,…,n。
定量指标按其性质可以分为盈利性指标与损耗性指标两类。对于盈利性指标,指标越小越差;对于损耗性指标,指标越大越不利[10]。因此规格化原则为:盈利性指标公式rij=yij/maxyij;损耗性指标公式为:rij=minyij/yij。

式中:i=1,2,…,m;j=1,2,…,n。
1.3.2 综合评判
各方案的优劣次序是根据权重向量和隶属度矩阵的积确定。

2 工程实例应用
山西平朔东露天矿首采区先后发生多次塌方(滑坡)事故,严重影响了东露天矿的安全生产。根据东露天矿滑坡的特点、地勘调查结果以及专家和管理者的建议,提出了3种可行的治理方案:清塌缓坡+预留宽平台(简称方案P1)、清塌缓坡+反压坡脚(简称方案P2)、清塌缓坡+注浆、锚索加固(简称方案 P3)。
2.1 构建层次结构模型
本次滑坡处治方案的参数层次结构模型包括目标层(A)、准则层(B)、指标层(C)。具体的目标影响因素的选取是根据东露天矿滑坡的实际勘探结果、分析情况和各方案的特点得出的。结构参数层次模型包括目标层:最优结构参数(A);准则层:经济指标(B1),安全因素(B2),技术指标(B3);指标层:工程总成本(C1),处治后稳定性(C2),压煤量(C3),耐久性(C4),施工工期(C5),施工难易程度(C6),方案灵活适应性(C7),降水/爆破震动对工程进展的影响(C8)(如图1所示)。

图1 平朔东露天矿滑坡处治方案的层次结构模型
根据方案的具体处治流程得出各方案的综合评价指标体系,见表4。

表4 各方案的综合评价指标体系
2.2 指标权重确定
根据表1可得,目标层对应于准则层的A-B因素判断矩阵(如表5所示)。

表5 A-B判断矩阵
A-B:λmax=3.054,CI=0.027,RI=0.52,CR=0.057<0.1,满足一致性检验要求,权重矩阵A=[0.19,0.33,0.48]可以接受。
同理,
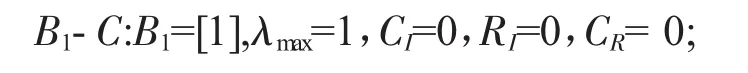

则可得层次总排序见表6。

表6 层次总排序表
层次总排序一致性检验为:CI=0.009,RI=0.605,CR=0.015<0.1,故层次总排序的判断矩阵满足一致性检验要求。因此,影响滑坡处治方案选择的归一化权重向量为 W=(0.190,0.330,0.050,0.116,0.050,0.082,0.028,0.154)。
2.3 隶属矩阵确定
a)指标体系中的定量指标处治后的稳定性、回收压煤量和施工工期所构成的特征向量矩阵为:

对特征向量矩阵进行规格化得:

b)指标体系中5个定性指标的隶属度矩阵
(a)根据各方案总造价成本的特点,得特征向量矩阵:

则隶属度矩阵为R1=[1,0.667,0.333].
(b)根据各方案耐久性的特点,得特征向量矩阵:

则隶属度矩阵为R4=[1,0.818,0.176].
(c)根据各方案施工难易程度的特点,得特征向量矩阵:

则隶属度矩阵为R6=[1,1,0.538].
(d)根据各方案灵活适用性的特点,得特征向量矩阵:

则隶属度矩阵为R7=[1,1,0.538].
(e)根据各方案的降水或爆破震动对工程进展的影响的特点,得特征向量矩阵:

则隶属度矩阵为R8=[1,0.333,0.429],综合隶属度矩阵为:

2.4 最优方案确定
所以,方案集的综合评判向量为:

因此,各方案的综合优越度为:方案一为95.0%;方案二为71.0%;方案三为51.6%,则方案的优劣次序依次为:方案一,方案二,方案三。故选方案一。
东露天矿滑坡处治的实践表明,采用的方案一能有效降低成本,施工安全,各项技术指标符合标准,且处治后的边坡稳定,取得了良好的效果。
3 结论
本文以平朔东露天矿东北帮滑坡处治方案优选为工程背景,分析研究了滑坡处治方案在多目标作用下的优选。最后,通过对综合评判向量的分析,得出了方案一是最优处治方案。主要研究结论如下:
a)运用模糊层次分析法对滑坡处治方案进行评价时,最关键的一步是建立合理的层次结构模型。构造成对比较矩阵是整个工作的数据基础。评价因子的权重由成对比较矩阵的权向量表示,能够较客观地反应评价因子的权重,得出的结果最大程度地反映了评价指标的真实性。
b)用模糊层次分析法对东露天矿滑坡处治方案进行分析,得出方案集的综合评判向量,从而选出方案一,在实际应用中也取得了良好的效果,能够做出更为科学、准确、有理论依据的判断,这种方法在滑坡处治领域的应用具有可行性。
c)采用此种方法进行滑坡处治方案优化研究有着广阔的前景,对其他类似的综合评价工作也有一定的借鉴意义。对于结构更为复杂、目标和影响因素更为细化的参数优选问题,权重向量和隶属度矩阵计算量将大大增加,可以将AHP-Fuzzy法和其他软件结合起来,广泛应用于多目标的决策分析中。
d)需要特别指出的是,对于定性指标,需要总结现场经验给出权重,因此要对现场特别熟悉且掌握丰富的理论知识。另外,在后续工作中应进一步建立起滑坡处治工程方案与工程可靠度计算的分析模型、施工组织设计等相关指标评价体系的关系,从而真正实现多目标优化设计,以完全消除人的主观影响。
