大地测量与地球物理中病态性问题的正则化迭代解法

顾勇为，归庆明，张 璇，魏 萌

1.信息工程大学 理学院，河南 郑州450001；2.中船重工集团 第七一三研究所，河南 郑州450015

1 引 言

求解大规模超定线性方程组是控制网平差、GPS导航定位、重力场向下延拓等大地测量与地球物理应用中频繁出现的问题，共轭梯度法（conjugate gradient method，CG）是目前求解此类方程组的有效方法之一，该方法在保证计算精度的前提下可显著提高运算速度，且只需要几百MB的内存空间，因此，应用十分广泛［1－5］。然而，以上应用领域呈现的问题又往往具有病态性，在相应的线性方程组中则呈现出系数矩阵具有严重的复共线性特征，此时单纯用CG方法解算将严重失真［1－2］。正则化方法是适合于消除或减弱复共线性危害的解算病态问题的一种主要方法，长期以来受到国内外学者的广泛关注，其研究成果不断涌现［4－12］。正则化理论的基本思想是将病态问题加上先验条件，以恢复问题的稳定性。通过正则化方法，可以将病态问题转化为病态性相对较轻的问题或良性问题［4－5］。由于实际工作的巨大需求，正则化方法的理论与应用研究在测量界发展迅猛［10－18］。文献［6］对测量领域中的不适定问题提出了正则化解的统一表达式。文献［7］在GPS快速定位等实际工作中充分考虑参数的物理信息和先验信息，并将其成功应用于正则化矩阵的构造和正则化参数的选取中。文献［8］在航空重力测量数据向下延拓中比较了多种延拓方法，最后发现正则化方法效果较佳，并提出了以均方误差极小值为目标确定正则化参数的方法。文献［9］在GPS中长基线实时系统误差估计中采用正则化方法，其模型中既有DD码观测又有载波相位（差）观测，待求参数为位置坐标和对流延迟，正则化矩阵设计思想是仅对相对准确的位置参数实施控制，体现了对先验信息已知的参数进行约束的选权拟合法思想。文献［10—11］挖掘利用复共线性的关键信息构造正则化矩阵，提出了基于复共线性诊断的正则化方法。文献［12］提出将广义岭估计用于求解航空重力向下延拓病态问题，通过确定多个正则化参数获得更小的均方误差。文献［13］利用广义正则化方法降低病态性对总体最小二乘求解的影响，以提高解算结果的稳定性。文献［14］利用GRACE数据解算重力场问题时采用了正则化方法，在构造正则化矩阵时利用了CSRRL04GRACE解误差的信息，在选取正则化参数时采用了L曲线投影变量法，极大地减少了计算量。文献［15］给出了4类可用于重力场解算的正则化矩阵（零次、一次、二次和Kaula），以及用于确定正则化参数的L曲线法和GCV方法的数学模型。文献［16］为避免正则化参数对航空重力向下延拓过程中可靠成分的修正影响，提出Tikhonov双参数正则化法。文献［17］提出了基于均方误差意义下的正则化参数的选取方法，具有较深入的理论意义。文献［18］利用TSVD正则化方法有效地解决了水坝监测模型中的复共线性问题。文献［19］提出了修正偏差的正则化方法，并分析了其优于普通正则化解的条件。

为了克服病态性对共轭梯度法的危害影响，文献［5］根据正则化思想，针对法矩阵的最小特征值改进算法，使解的精度获得提高。然而，实际工程技术中法矩阵往往具有多个小特征值对模型求解构成危害，仅考虑克服最小特征值对解算结果的影响是不够的。因此本文在该方法的基础上深入研究，从理论上提出了克服多个小特征值的解法，使解算方程的病态性降低到适当的水平，给出了具体的实施方法及步骤，最后通过算例验证了新解法的有效性。

2 数学模型及共轭梯度法解法

大地测量与地球物理中大量的问题可归结为对如下观测方程的求解［1］

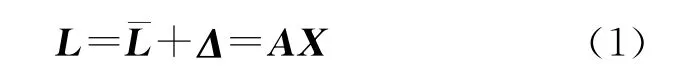
式中，L为n×1观测向量为n×1观测真值向量；Δ为n×1观测误差向量；A为n×t系数阵；rank（A）＝t，X＝［X1X2…Xt］T为t×1未知参数向量。式（1）具有如下统计特征

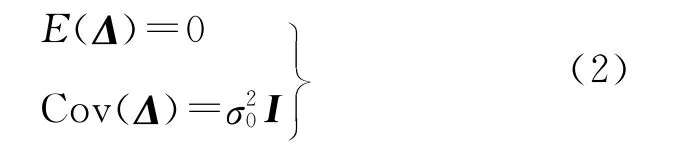
式中，σ20为未知单位权方差；单位阵I为观测权阵（观测权阵若不是单位阵，可将其单位化［7］）。由于式（1）为超定方程组，因此没有常规解，只有最小二乘（least square，LS）解。在式（1）的两边同乘以AT，得到法方程

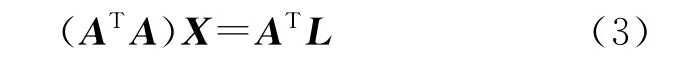
式（3）可简化为

式中，N＝ATA；Y＝ATL。解之得未知参数X的LS估计

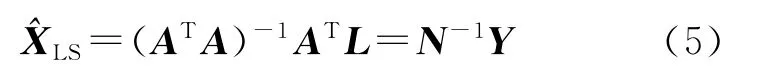
当线性方程组为大规模超定方程组时，共轭梯度法是一种常用的有效解法［1－3］。其步骤简述如下。

步骤1：选取初值X0。

步骤2：计算残差r0＝Y－NX0，令p0＝r0，α0＝，得到首次迭代结果X1＝X0＋α0p0。计算r1＝Y－NX1以备用。

步骤3：对于k＝1，2，…，n，重复以下迭代过程：计算pk＝rk＋βk－1pk－1，其中算得迭代结果Xk＋1＝Xk＋αkpk，计算rk＋1＝Y－NXk＋1。若rk＋12＜ε（式中，·2表示欧氏二范数，以下相同），停止迭代，转入步骤4；否则继续迭代。

步骤4：将最后的Xk＋1作为近似解，＝Xk＋1。

共轭梯度法在求解大规模超定的线性方程组时效果显著，但是当线性方程组具有病态性时则出现失效、收敛速度太慢等问题。目前解算病态问题应用较广的方法是Tikhonov正则化方法，它是针对不适定问题提出来的，对于线性模型式（1），其估计准则为

使Φ达到最小的参数X即为所要求的解。式（6）的第一项为残差平方和，第二项Ω（X）称为稳定泛函，通常取Ω（X）＝X2H＝XTHX，式中，H为正则化矩阵。由此得到正则化解

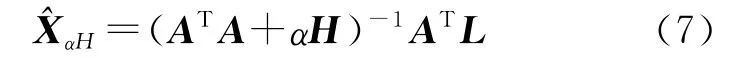
正则化思想的核心是通过修正法矩阵，使解算方程的条件数大大降低，病态性大大减弱，因而其普适性强、应用广泛。如果将正则化思想与共轭梯度法相结合，则改善的共轭梯度法就能够用以求解病态性问题，下面将对此展开研究。

3 基于条件数控制的正则化迭代解法

3.1 干扰源向量与修正法矩阵

设法矩阵ATA的特征值为0＜λ1＜λ2＜…＜λt，相应的单位正交化特征向量为t×1向量e1、e2、…、et。法矩阵的病态性不仅表现在其最小特征值λ1相对于最大特征值λt很小，而且在多数情况下，法矩阵具有s个相对于最大特征值λt很小的特征值，即λ1＜λ2＜…＜λs＜＜λt。本文利用正则化思想修正或改造这些小特征值，获得可以替换ATA的修正法矩阵，进而对法方程作改进，使修正法方程与原法方程相比，病态性减弱到便于稳定解算的程度。为了对ATA的病态性进行干扰，构造以下n×1向量

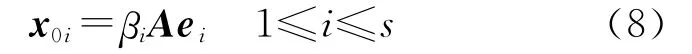
式中，βi＞0，称x0i为干扰源向量。利用干扰源向量x0i，设t×1向量

设

由e1，e2，…，et的正则性可得

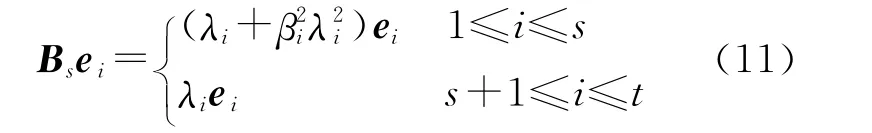
式中，Bs是通过对法矩阵ATA改造获得的，称其为修正法矩阵。由式（11）可知，修正法矩阵Bs的t个特征值为λi＋βi2λi2（1≤i≤s）和λi（s＋1≤i≤t），特征向量仍为e1、e2、…、et。

由此可见，与ATA相比，Bs的条件数减少，由式（8）、式（9）可知，干扰源向量x0i的构造，或参数βi的选取是决定Bs的病态性的关键所在。干扰源向量的个数s的确定是另一个关键所在。

3.2 参数s及β1、β2、…、βs 的选取

干扰源向量的个数s以及β1、β2、…、βs的取法关系到法矩阵病态性被修正的程度，若s过小则修正不足，s过大则可能由于计算过程复杂引入过大的误差，损害新旧方程的同解特性（下文详述）。β1、β2、…、βs的选取则要考虑新方程的条件数被切实降低。为此对参数选取的总体策略是在满足病态性降低到一定水平的条件下，干扰源向量的个数s尽量少。s以及β1、β2、…、βs的具体取法考虑如下。

（1）求出ATA的特征值为0＜λ1＜λ2＜…＜λt，计算cond（ATA），为修正法矩阵条件数的确定提供参考。

（2）确定修正法矩阵条件数K。根据实际问题，将法矩阵的条件数降低几个数量级，即可达到明显的效果，如本文针对航空测量数据向下延拓问题，选500较合适。

（3）计算条件指标［20］按其是否大于K分为两类：第一类的条件指标过大，相应的特征值λ1、λ2、…、λs过小，应作修改，由此确定s。

（4）对于过小的特征值λ1、λ2、…、λs，利用其对应的特征向量按照式（8）构造相应的干扰源向量，其中参数β1、β2、…、βs的取法为

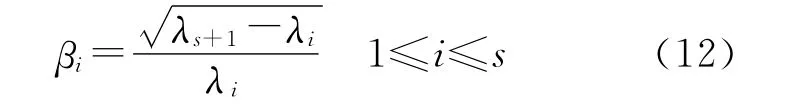
由式（12）可知λi＋βi2λi2＝λs＋1（1≤i≤s），又因修正法矩阵Bs的t个特征值为λi＋βi2λi2（1≤i≤s）和λi（s＋1≤i≤t），可知

3.3 修正法方程与基于条件数控制的正则化迭代解法

由式（8）、式（9）及式（1）可知

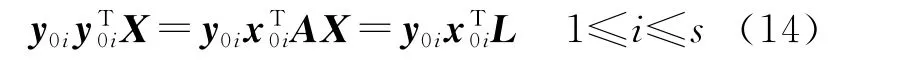
将式（3）与式（14）（1≤i≤s，共s个）相加，得到与式（3）同解的方程

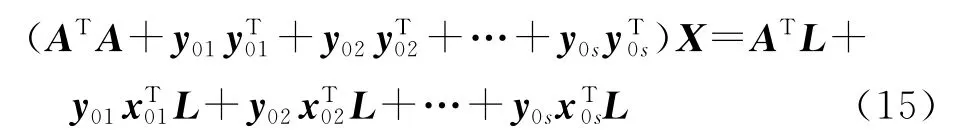
简记为

式中，Bs＝ATA＋y01yT01＋y02yT02＋…＋y0syT0s；Ls＝ATL＋y01xT01L＋y02xT02L＋…＋y0sxT0sL。式（16）是为改善法方程式（3）的病态性而对其进行的一种修正，称其为修正法方程。至此，病态方程式（3）转化为相对良态的方程式（16），用共轭梯度法求解即可生效。特别值得注意的是，式（3）和式（16）理论上是同解的，这是一般的正则化方法所不具有的良好性质。该结论是本文将文献［5］的结论推演后得到的结论，文献［5］给出了本算法当s取1时的一个特例，对本算法的形成提供了启发。

在进行装配过程中的信息追溯时，基于所建立的航空发动机装配过程中的两层数据世系，给出如下时间区间队列和数据快照的定义

综上所述，本文提出的算法主要分为3步：

步骤1：利用对法矩阵谱分解获得的特征值与特征向量确定干扰源向量的个数、构造干扰源向量，进而构造修正法矩阵。

步骤2：利用干扰源向量及其特性，将法方程改造为修正法方程。

步骤3：用共轭梯度法解算修正法方程。称该方法为基于条件数控制的正则化迭代解法（regularization based on controlling condition number，RBC）。

4 算例及分析

算例1：线性方程组L＝ˉL＋Δ＝AX，式中

未知参数的真值为X＝ ［1 1 1 1 1 1 1 1 1 1 ］T。为了比较几种算法的解算效果，本文分别用LS估计、CG估计、Tikhonov估计和RBC估计对该问题进行解算，并计算其均方差作为精度，得到的结果见表1。

表1 4种算法的解算结果及精度Tab.1 The results and accuracies for the four solutions

从解算结果可以看出，LS估计严重失真，CG方法和两种正则化方法均有效改善了LS估计求解的质量，而按新提出的RBC估计解算则达到了较高质量。

改正一个和多个特征值对估计结果的影响相差较大。从一个到多个一开始逐渐变好，但改正的个数达到一定程度后，继续修改则效果不明显（或效果开始变差）。通过试验，按本文的修改方法效果较好，该问题将另文作进一步深入研究。

算例2：航空重力测量数据向下延拓模拟试验。在2°×2°的某丘陵区域由EGM2008模型生成576个网格点的重力异常数据，将其作为真值，如图1所示。将地面数据向上延拓至空中3400m［11］比地面区域稍大的区域内，并作正态随机扰动，形成空中重力测量数据的模拟观测值。本文按4种方式进行延拓解算：LS、CG、Tikhonov、RBC，并求出各种解值的均方差，作为精度指标考察求解质量［11］。解算结果见图1—图5及表2。

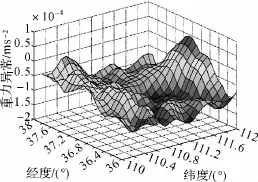
图1 重力异常真值Fig.1 True value of gravity anomaly

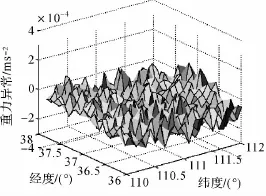
图2 重力异常的LS解Fig.2 LS solution of gravity anomaly

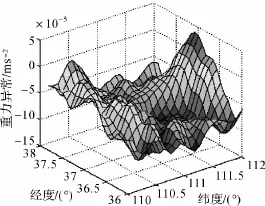
图3 重力异常的CG解Fig.3 CG solution of gravity anomaly

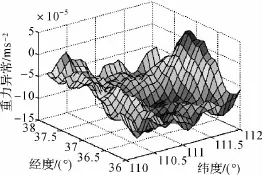
图4 重力异常Tikhonov正则化解Fig.4 Tikhonov solution of gravity anomaly

图5 重力异常的RBC正则化解Fig.5 RBC solution of gravity anomaly

表2 4种解的统计分析Tab.2 Statistical analysis of the four solutions ms－2

可以看出，LS估计解算效果严重失真，CG、Tikhonov和RBC均可改善求解质量，而RBC改善求解质量效果最佳。

5 结 论

共轭梯度法是解算大型线性方程组的常用方法，具有解算精度高、数据存储方便等优点，但是大地测量与地球物理应用中经常出现的问题具有强病态性，甚至是超强病态性，使得共轭梯度法在这种情形下失效。本文对此进行了深入的研究，提出了基于条件数控制的正则化迭代解法。通过对法矩阵作谱分析，构造干扰源向量，改造病态的法方程为修正法方程，使解算方程的病态性减弱到适当的水平，在此基础上用共轭梯度法解算，得到了良好的效果。新算法较好地将正则化思想结合到共轭梯度法之中，在理论上具有一定的价值。通过算例表明了该算法的有效性及与相关算法比较的优越性，特别在航空重力向下延拓的解算试验中获得成功，对于大地测量病态性问题的求解具有一定的应用价值。

［1］ ZHENG Wei，XU Houze，ZHONG Min，et al.Accurate and Rapid Determination of the GRACE Earth’s Gravitational Field Using the Improved Pre－conditioned Conjugate－gradient Approach and Three－dimensional Interpolation Method［J］.Progress in Geophysics，2011，26（3）：805－812.（郑伟，许厚泽，钟敏，等.基于改进的预处理共轭梯度法和三维插值法精确和快速解算GRACE地球重力场［J］.地球物理学进展，2011，26（3）：805－812.）

［2］ LIU C S，ATLURI S N.An Iterative Method Using an Optimal Descent Vector for Solving an Ill－conditioned System Bx＝b Better and Faster than the Conjugate Gradient Method［J］.Computer Modeling in Engineering and Sciences，2011，80（3）：275－298.

［3］ XU Shufang，GAO Li，ZHANG Pingwen.Numerical Linear Algebra［M］.Beijing：Beijing University Press，2000：139－160.（徐树方，高立，张平文.数值线性代数［M］.北京：北京大学出版社，2000：139－160.）

［4］ XU Peiliang，YOICHI F，LIU Yumei.Multiple Parameter Regularization：Numerical Solutions and Applications to the Determination of Geopotential from Precise Satellite Orbits［J］.Journal of Geodesy，2006，80（1）：17－27.

［5］ LIU C S，HONG H K，ATLURI S N.Novel Algorithms Based on the Conjugate Gradient Method for Inverting Illconditioned Matrices，and a New Regularization Method to Solve Ill－posed Linear Systems［J］.Computer Modeling in Engineering and Sciences，2010，60（3）：279－308.

［6］ OU Jikun.Uniform Expression of Solutions of Ill－posed Problems in Surveying Adjustment and the Fitting Method by Selection of the Parameter Weights［J］.Acta Geodaetica et Cartographica Sinica，2004，33（4）：283－288.（欧吉坤.测量平差中不适定问题解的统一表达与选权拟合法［J］.测绘学报，2004，33（4）：283－288.）

［7］ WANG Zhenjie.Regularization of Ill－posed Problems in Surveying［M］.Beijing：Science Press，2006：66－85.（王振杰.测量中不适定问题的正则化解法［M］.北京：科学出版社，2006：66－85.）

［8］ WANG Xingtao，XIA Zheren，SHI Pan，et al.A Comparison of Different Downward Continuation Methods for Airborne Gravity Data［J］.Chinese Journal of Geophysics，2004，47（6）：1017－1022.（王兴涛，夏哲仁，石磐，等.航空重力数据向下延拓方法比较［J］，地球物理学报，2004，47（6）：1017－1022.）

［9］ LUO Xiaowen，OU Jikun，YUAN Yunbin.An Improved Regularization Method for Estimating Near Real－time Systematic Errors Suitable for Medium－long GPS Baseline Solution［J］.Earth Planets Space，2008，60：793－800.

［10］ GU Yongwei，GUI Qingming，BIAN Shaofeng，et al.Comparison between Tikhonov Regularization and Truncated SVD in Geophysics［J］.Geomatics and Information Science of Wuhan University，2005，30（3）：238－241.（顾勇为，归庆明，边少锋，等.地球物理反问题中两种正则化方法的比较［J］.武汉大学学报：信息科学版，2005，30（3）：238－241.）

［11］ GU Yongwei，GUI Qingming.Study of Regularization Based on Signal－to－Noise Index in Airborne Gravity Downward to the Earth Surface［J］.Acta Geodaetica et Cartographica Sinica，2010，39（5）：458－464.（顾勇为，归庆明.航空重力测量数据向下延拓基于信噪比的正则化方法的研究［J］.测绘学报，2010，39（5）：458－464.）

［12］ JIANG Tao，LI Jianchen，WANG Zhengtao，et al.Solution of Ill－posed Problem in Downward Continuation of Airborne Gravity［J］.Acta Geodaetica et Cartographica Sinica，2011，40（6）：684－689.（蒋涛，李建成，王正涛，等.航空重力向下延拓病态问题求解［J］.测绘学报，2011，40（6）：684－689.）

［13］ GE Xuming，WU Jicang.Generalized Regularization to Ill－posed Total Least Squares Problem ［J］.Acta Geodaetica et Cartographica Sinica，2012，41（3）：372－377.（葛旭明，伍吉仓.病态总体最小二乘问题的广义正则化［J］.测绘学报，2012，41（3）：372－377.）

［14］ SAVE H，BETTADPUR S，TAPLY B.Reducing Errors in the GRACE Gravity Solutions Using Regularization［J］.Journal of Geodesy，2012，86（4）：695－711.

［15］ XU Xinyu，LI Jiancheng，WANG Zhengtao，et al.The Simulation Research on the Tikhonov Regularization Applied in Gravity Field Determination of GOCE Satellite Mission［J］.Acta Geodaetica et Cartographica Sinica，2010，39（5）：465－470.（徐新禹，李建成，王正涛，等.Tikhonov正则化方法在GOCE重力场求解中的模拟研究［J］.测绘学报，2010，39（5）：465－470.）

［16］ DENG Kailiang，HUANG Motao，BAO Jingyang，et al.Tikhonov Two－parameter Regulation Algorithm in Downward Continuation of Airborne Gravity Data［J］.Acta Geodaetica et Cartographica Sinica，2011，40（6）：690－696.（邓凯亮，黄谟涛，暴景阳，等.向下延拓航空重力数据的Tikhonov双参数正则化方法［J］.测绘学报，2011，40（6）：690－696.）

［17］ SCHAFFRIN B.Minimum Mean Squared Error Adjustment and the Optimal Tykhonov－Phillips Regularization Parameter via Reproducing Best Invariant Quadratic Uniformly Unbiased Estimates［J］.Journal of Geodesy，2008，82（2）：113－121.

［18］ XU Chang，DENG Chengfa.Solving Multicollinearity in Dam Regression Model Using TSVD ［J］.Geo－spatisl Information Science，2012，14（3）：230－234.

［19］ SHEN Yunzhong，XU Peiliang，LI Bofeng.Bias－corrected Regularized Solution to Inverse Ill－posed Models［J］.Journal of Geodesy，2012，86（8）：567－608.

［20］ GUI Qingming，YAO Shaowen，GU Yongwei，et al.A New Method to Diagnose Multicollinearity Based on Condition Index and Variance Decomposition Proportion［J］.Acta Geodaetica et Cartographica Sinica，2006，35（3）：210－214.（归庆明，姚绍文，顾勇为，等.诊断复共线性的条件指标—方差分解比法［J］.测绘学报，2006，35（3）：210－214.）