月面巡视探测器远距离单摄站定位及精度分析

徐辛超，徐爱功，刘少创，马友青，魏士俨

（1.辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000；2.中国科学院 遥感应用研究所，北京 100101）

1 引言

探月工程作为国家重大科技专项，是我国在发展人造卫星和载人航天之后，空间科学和技术发展的第三个里程碑。我国的探月工程分为 “绕、落、回”三期［1］。目前探月一期已经取得了圆满成功并获取了大量珍贵的科研数据。我国科学家在广泛论证调研的基础上，提出了探月二期工程实施 “着陆器软着陆以及月球车巡视勘察”的总体科学目标［2］。准确可靠的定位技术是巡视探测器导航和路径规划及实现科学探测目标的重要保障。

巡视探测器会安装惯性导航系统和里程计，通过这两者进行相对定位具有可靠的短期精度、绝对的实时性和完全的自主性，但由于存在误差积累，其测量精度会随时间而降低，不能够完全适合于月面巡视探测器的长时间、长距离导航定位。针对巡视探测器在远距离状态下的高精度定位需求［3－4］，本文提出了采用基于全景影像的交会定位方法。该方法的定位精度不受行走距离的影响，不存在累积误差，并且可以通过对目标的多余观测进行平差处理，提高定位结果的精度和可靠性。本项目的研究成果可以服务于即将发射的“嫦娥三号”任务。

2 远距离单摄站定位算法关键技术

在巡视探测器移动过程中拍摄的影像内控制点的数量不足4个的情况下，可以将获取的全景序列影像进行匹配和拼接，然后采用远距离单摄站定位技术对其进行定位。远距离单摄站定位方法的关键技术主要包括：全景影像拼接技术和远距离单摄站定位技术。

2.1 全景影像拼接技术

由于巡视探测器上搭载了两台全景相机和两台导航相机，旋转拍摄时，两对相机固定在桅杆的两端且主光轴平行。桅杆围绕着其中心转轴进行旋转，每次旋转θ角就进行一次拍摄，对获取的影像进行拼接，就可以制作360°柱状全景影像。生成全景影像包括三大过程：影像预处理、特征点匹配和匹配约束。

月面影像中，由于组成月壤的成分反差较小，采用普通的滤波进行影像预处理不能达到预期要求，因此，本文采用Wallis滤波对影像进行预处理［5］，可以大幅度增强影像中不同尺度的影像纹理模式，将影像中反差小的区域的反差增强，即使得影像中灰度的微小变化信息得到增强，在提取影像中的点特征时可提高点特征的数量和精度，而在影像匹配中则可以提高匹配结果的可靠性和精度。此外，在计算影像的局部灰度方差和均值时使用了平滑算子，在增强影像有用信息的同时抑制了噪声，提高了影像的信噪比。

由于全景相机获取的月面影像中，纹理信息较为匮乏，且靠近和远离巡视探测器的位置尺度变化较大，因此，本文采用尺度不变特征变换（scale－invariant feature transform，SIFT）算法进行匹配［6］。SIFT特征描述了具有抗旋转和一定程度的抗尺度变化的特性，在纹理信息较为缺乏的情况下也能够得到较多的SIFT特征向量，能够较好的满足匹配的要求［7］。

由于在从三维空间向二维影像投影的过程中丧失了大量的信息，要实现从二维影像重建三维环境，就必须充分利用所要解决的问题中包含的约束条件以限制其解空间的大小，即匹配的搜索范围［8－9］。完成了匹配计算之后，可能存在错误的对应关系，所以也要利用约束条件剔除误匹配点对。本文采用了唯一性约束、核线几何约束和仿射变换约束对匹配结果进行约束［10］。

2.2 远距离单摄站定位

根据影像序列可以制作全景影像，并可以通过在影像中选取3个控制点求解巡视探测器的位置坐标。方法的原理为：A、B、C为已知控制点，P点为摄站点，观测P点至A、B、C各方向的夹角［11］，根据控制点坐标以及其在全景影像中对应的像素坐标，即可推算P点的坐标。图1为摄站位置与控制点位置在三种不同情况下的分布示意图。

图1 摄站点与控制点分布情况示意图

首先，求取摄站P点到A、B、C各方向的夹角。A、B、C点位于全景影像上，参照着陆器下降影像或嫦娥二号卫星影像中控制点的位置，在全景影像中选取相应的像点，并量取其在影像中的像素坐标。然后，根据三个点在全景影像中的位置以及相机的旋转角度可以推算在摄站P至A、B、C各方向的水平夹角（α，β，λ），如图2所示。由于算法中生成的全景影像为360°柱面全景影像，三个对应角满足以下关系

图2 水平角示意图

令三角形ABC面积为SABC；BPC面积为SA、APC面积为SB、APB面积为SC，可得

整理得

改写为坐标计算公式

同理得

做三角形ABC的外接圆，延长BP与圆交于E；延长AP与圆交于F；延长CP与圆交于G。可得

由于EPPB＝FPPA＝GPPC令：PA＝1／（cotA－cotα），PB＝ 1／（cotB－cotβ）、PC＝1／（cotC－cotγ），推导出巡视探测器位置坐标计算公式

根据式（6）即可得到巡视探测器的平面位置坐标。

在实际计算过程中，可以采用多次观测进行平差，即当控制点的数量多于3个时，可以进行平差解算，得到最优解。

2.3 全景影像拼接实验

远距离单摄站定位方法流程如图3所示。

图3 远距离单摄站定位流程

1）根据 “嫦娥二号”探月卫星和着陆器下降过程中获取的着陆区高分辨率遥感影像提取得到着陆区附近范围内的特征点，即控制点坐标，得到控制点库。

2）利用当前摄站导航相机和全景相机的相机参数、拍摄全景影像时桅杆的旋转角度参数等完成影像匹配、全景影像拼接；

3）在全景影像中提取特征点并记录其像素坐标，并与步骤1）中得到的控制点库中的点进行对比，寻找与之相对应的控制点，并判断控制点数量是否满足要求，只有控制点数量大于3个时才可完成定位过程；

4）根据步骤3）中控制点的像素坐标求解摄站到各个控制点方向的夹角；

5）根据控制点坐标和其对应的像素坐标进行摄站坐标求解，如有多余观测，则进行相应的平差，以提高最终定位精度。

3 实验分析

本文设计了两组不同的实验，其中全景影像拼接实验用于验证影像拼接效果，远距离定位实验用于测试本文所提出算法的定位精度及影响因素。

3.1 全景影像拼接实验

本文的实验数据在格尔木市以南的空旷戈壁滩进行采集，以求模拟巡视探测器在单摄站获取的影像最大程度的与月表真实情况接近。全景影像生成过程中首先需要对相邻两幅影像进行匹配和拼接。图4为采用本文特征提取方法得到的相邻影像匹配点提取结果。

图4 相邻影像匹配结果

由图4可以得到：在图中相邻影像的重叠区域，本文特征提取方法能够得到101个匹配点，且仅存在2个误匹配点，完全能够达到本文定位算法的需求。

图5为模拟巡视探测器行进路线上6号摄站完成的全景影像，标记部分为所提取的与控制点库中相对应的全景影像中的控制点。

图5 摄站6的全景影像

由上述全景影像拼接结果表明：本文采用的影像的柱面投影算法有效的消除了图像之间可能存在的重复景物信息，在实验场地光照强烈的情况下，仍能够保持较小的拼接痕迹，相邻影像间可以较为平滑的过渡。此外，360°柱面全景影像拼接又提供了一种更加真实、连续的实景展示方式，为提高控制点提取精度提供了基础。同时，本文算法在全景影像拼接过程中尽可能的保持其最原始的状态，相邻影像在拼接时仅有非常小的变形，有效的提高了控制点像素坐标的提取精度。

3.2 远距离定位实验

为了验证提出的远距离单摄站定位方法的定位精度及影响因素，本文在地表与月表较为接近的戈壁滩设计了以下实验，第一组实验为模拟巡视探测器行进路线上每隔一定距离完成一个摄站的全景影像拍摄，并根据拼接完成的影像进行定位；第二组实验为在同一摄站全景影像条件下，采用不同的控制点进行定位。图6为购买的实验区部分快鸟影像（用于模拟嫦娥二号获取的着陆区高分辨率影像），标出部分S编号的点为实验过程中的摄站，其余点为部分提取的控制点，即地面上有明显特征的点，而在采用真实月面影像进行定位时，可以采用全景影像中的月面撞击坑特征点作为为控制点进行定位。控制点在独立坐标系下的坐标如表1所示。

图6 实验区部分快鸟高分辨率影像

表1 控制点坐标数据

实验中的摄站坐标采用全站仪实测数据作为真值，不同定位算法的定位结果与之进行比较，以分析算法定位精度。摄站坐标采用全站仪反射片观测获取，X、Y坐标通过将反射片置于过相机摄影中心的铅垂线上观测得到。

事先进行相机标定，获取的一系列参数如表2所示。

实验模拟巡视探测器由距着陆器100m的距离开始，每隔一定距离进行全景影像拍摄。各个摄站拍摄的影像中，距离相机较近的部分分辨率较高，而远离相机的分辨率较低。利用本文远距离单摄站方法进行定位，得到模拟路线上的定位结果与全站仪实测数据偏差如图7所示。

表2 相机参数表

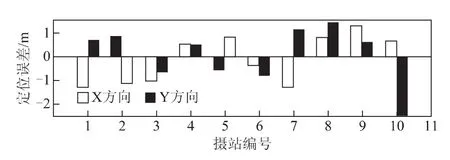
图7 各摄站定位误差

由上述定位结果可得：

（1）各个摄站中最小定位误差为0.746m，最大定位误差为2.571m，平均定位误差1.414m。本文提出的远距离单摄站定位方法是可行并且较为稳定的。实验中的11个摄站中有10个摄站都能较好的完成定位，并且定位误差满足巡视探测器远距离定位精度要求。

（2）本文提出的远距离定位方法最终定位结果的精度不受巡视探测器驶离着陆器的距离影响，各个摄站的定位误差小于3m。观测条件较好的4号和6号摄站，可用于定位的控制点较多且观测环境较好，定位精度可优于1m；10号摄站只有3个控制点可供应用，其中1个控制点观测环境较差，导致定位精度降低。

为了验证控制点数量与定位精度的关系，本文对观测条件好的6号摄站进行了进一步实验。图8为分别选择不同数量的控制点进行定位后的定位误差。图9为在10个控制点中，任意选择不同的3个控制点进行组合，并完成定位的误差，横轴代表不同的控制点组合。

图8 6号摄站摄站不同数量控制点下的定位误差

由上述定位结果可得：

（1）在全景影像中只要可以找到与控制点库中相对应的至少3个控制点即可完成定位。一般情况下，当控制点数量增加到4至5个时，定位精度会有较大程度的提高；当控制点数量进一步增加时，定位精度不会显著提高。

图9 6号摄站摄站不同控制点组合（任意3个控制点组合）下的定位误差

（2）控制点精度会影响定位精度，剔除该点后精度会提高。如图8中当7个控制点参与定位时，多余控制点使得定位精度反而有所降低，原因是多余的控制点位于相邻影像的拼接缝处，控制点像素坐标精度相对较低，当剔除该控制点后，定位精度会有一定程度的提高。当只有3个控制点可供定位时，定位结果的精度取决于控制点的观测质量，控制点观测条件较好，则提取精度较高，最终的定位结果也较好。

（3）当控制点在立体全景影像中的位置距离摄站较近时，最终定位结果精度较高，而控制点距离摄站位置较远时，定位结果的精度会降低。原因是距离摄站较近的影像分辨率较高，其对应的像素坐标提取精度较高，远离摄站的控制点分辨率较低，其对应的像素坐标提取精度较低，从而造成对定位结果的影响。

（4）不同控制点与摄站间的夹角对定位结果有一定影响，不同控制点与摄站间的夹角差异较小时定位误差较小，如图9中的8、9定位过程；而夹角差异较大时，定位误差会增大，如图9中的2、6、10定位过程。

综合分析上述实验可得：控制点的测量精度取决于嫦娥二号着陆区影像的分辨率，对最终定位结果有较大影响；控制点对应像素坐标的提取精度取决于全景影像的拼接缝的处理、影像的变形等；控制点的分布由巡视探测器所处的位置决定，当分布较为均匀时定位效果最好；要完成定位则影像中可用控制点数量必须大于3个，当控制点数量小于3个时，无法完成定位。

4 结束语

本文针对探月工程中巡视探测器在远离着陆器后的高精度定位需求，提出了基于全景影像的远距离单摄站定位方法，并对定位方法的可行性和精度进行了分析。通过对实验结果分析可得到以下几点结论：

（1）通过巡视探测器在单摄站获取的全景影像进行定位是可行的，在实验中的11个摄站，仅仅有1站由于控制点数量不足无法完成定位。

（2）影响本文方法定位精度的因素包括：控制点数量、控制点提取精度、全景影像中控制点的分布情况、全景影像的拼接质量等因素。

（3）当单摄站的全景影像中可用控制点数量小于3个或者需要确定巡视探测器的三维坐标时，需要研究其它定位方法来完成定位。

本文的研究成果可服务于即将发射的 “嫦娥三号”所携带的月面巡视探测器的远距离定位、导航服务。

［1］ 叶培建，张熇，饶炜.积极应对深空探测的技术挑战［J］.航天器工程，2006，15（3）：1－7.

［2］ 欧阳自远，李春来，邹永廖，等.我国月球探测一期工程的科学目标［J］.航天器工程，2005，14（1）：1－5.

［3］ 贾阳，陈建新，张熇.月面巡视探测器关键技术分析［J］.航天器工程，2006，15（3）：54－58.

［4］ 石德乐，叶培建，贾阳.对我国月面巡视探测器定位方法的一些思考［J］.航天器工程，2006，15（4）：14－20.

［5］ 张力，张祖勋，张剑清.Wallis滤波在影像匹配中的应用［J］.武汉测绘科技大学学报，1999，24（1）：24－28.

［6］ LOWE D G.Distinctive Image Features from Scale－invariant Keypoints［EB／OL］.（2004－01－05）［2013－07－18］.http：／／www.cs.ubc.ca／～lowe／papers／ijcv04.pdf.

［7］ 李芳芳，贾永红，肖本林，等.利用线特征和SIFT点特征进行多源遥感影像配准［J］.武汉大学学报：信息科学版，2010，35（2）：233－236.

［8］ 张登荣，俞乐，蔡志刚.点特征和小波金字塔技术的遥感图像快速匹配技术［J］.浙江大学学报：理学版，2007，34（4）：465－468.

［9］ 张继贤，李国胜，曾钰.多源遥感影像高精度自动配准的方法研究［J］.遥感学报，2005，9（1）：73－77.

［10］ MIKOLAJCZYK K，SCHMID C.An Affine Invariant Interest Point Detector［EB／OL］.（2010－12－21）［2013－07－18］.http：／／hal.inria.fr／docs／00／54／82／52／PDF／mikolajc＿ECCV2002.pdf.

［11］ 王之卓.摄影测量原理［M］.武汉：武汉大学出版社，2007.