中间法三角高程法应用于深基坑立柱隆沉监测

姚海敏

（上海中测行工程检测有限公司，上海市 200438）

1 概述

基坑施工的安全一直是保证工程建设安全的重中之重，越来越深越发受到人们的关注。基坑监测的作用是发现基坑在施工过程中的变形，是信息化施工的有效手段，而因土体卸载导致的立柱隆起，直接影响到整个支护体系的稳定性，是基坑监测规范中规定的重要监测项目。常规的立柱隆沉监测一般采用水准测量的方法，但是在实际工作中，深基坑深度都在5 m以上，一旦基坑开挖到一定深度，立柱监测点的监测就变得十分困难和危险，特别是钢支撑，必须采取保护措施。当支撑采用钢支撑，特别是单根钢支撑时，因支撑悬空难以行走而无法利用常规水准测量手段对立柱的隆沉进行监测。在这种情况下，常用于高程测量的三角高程法能否直接用于立柱隆沉监测呢？本文介绍的中间法三角高程的测量方法可以通过利用监测工作的特点，不量取仪器高和棱镜高，避免或削弱各误差源影响。用此方法测得的结果精度有较高保证，可代替等级水准测量。

2 三角高程测量原理及误差传播

全站仪三角高程测量是全站仪除水准测量外常用的高程测量方法，这种测量方法的优点是测量速度快，距离远，测量高差大，在跨河及山区低精度要求的高程测量中经常得到应用。它的测量原理如图1所示，在A点架设仪器，在B点安置棱镜，设仪器高为i，棱镜高为v，此时可测得全站仪中心至棱镜中心的距离为S和全站仪视线与水平面的夹角α。根据大气折光原理和地球曲率的概念，可计算得到A、B两点间高差为：

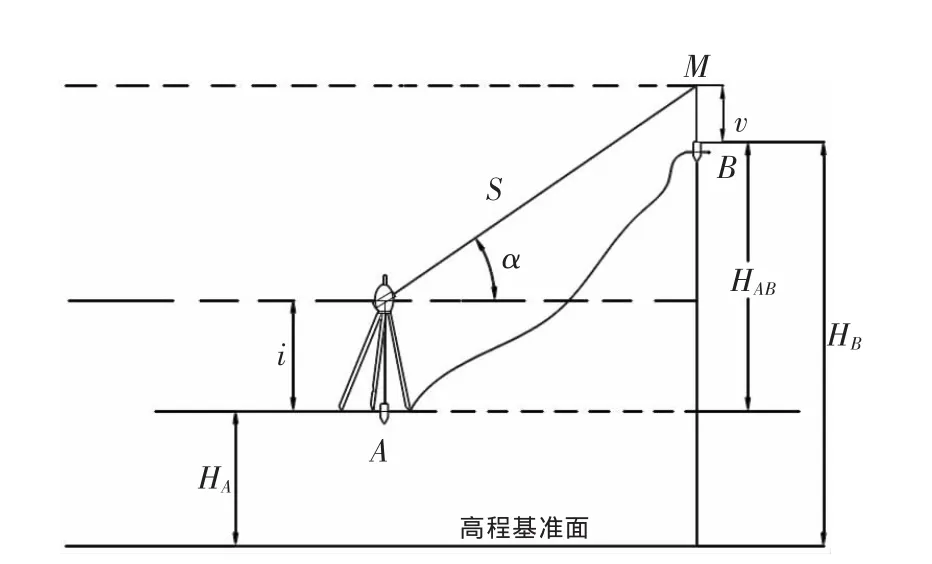
图1 三角高程测量原理图

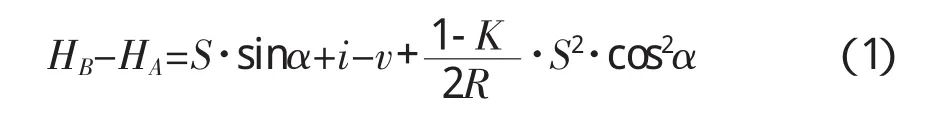
式中：i——仪器高；

v——为棱镜高；

R——为地球半径；

K——为大气折射系数。

式（1）即为三角高程测量高差的计算公式，公式中的每个因子包含误差，导致其组成的函数也受误差的影响，这就是误差传播。误差传播定律包括线性函数的误差传播定律、非线性函数的误差传播定律。非线性函数计算误差时要对公式两边取全微分[1]。

根据误差传播定律，式（1）两边取全微分，得：

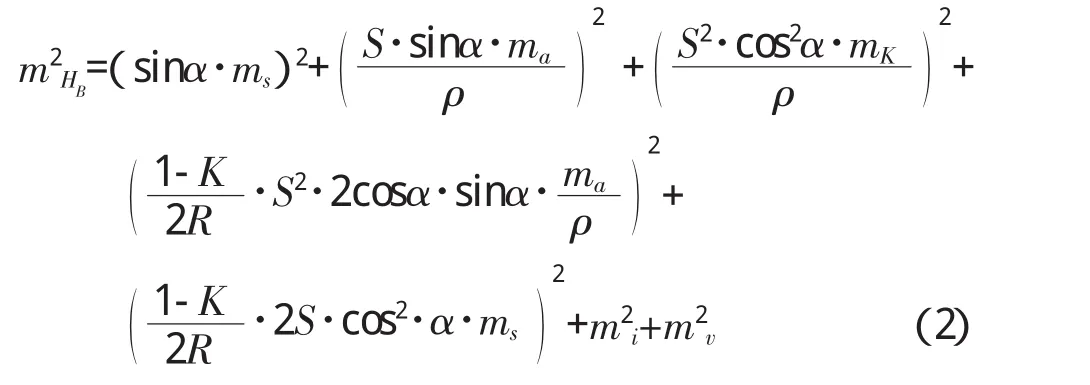
式中：mh——A、B两点间的高差中误差；

ms——全站仪所测斜距S的中误差；

mα——全站仪所测竖直角的中误差；

mK——大气折光系数的中误差；

mi——仪器高量取中误差；

mv——棱镜高量取中误差。

K值取通用的0.14[2]，S<100 m范围内，经计算的计算结果均小于0.01 mm，故此两项可忽略不计，所以式（2）左右各取平方根得：

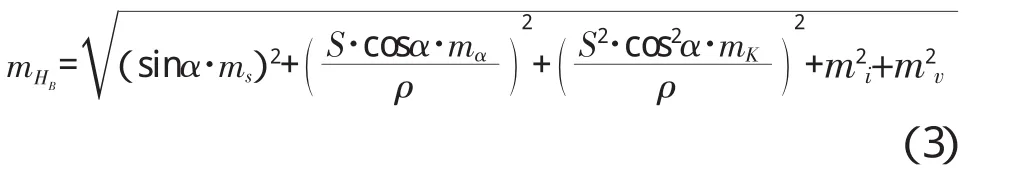
可见，传统的三角高程测量方法中，测量结果的精度的主要影响因素包括全站仪测距和测角精度、仪器高和棱镜高量取的误差、地球曲率、大气折光。可见，常规的三角高程测量误差源较多，精度难以控制。

监测工作的目的是获得监测对象的变化量，而无需知道监测对象的绝对量。常规的几何水准测量可以利用这一特点，如果能将全站仪象水准仪一样任意置点,而不是将它置在已知高程点，同时又在不量取仪器高和棱镜高的情况下，利用三角高程测量原理测出待测点的高程,那么测量精度将得到一定的保证。

3 应用及误差分析

3.1 中间法三角高程的特点

中间法三角高程测量法与水准测量的原理类似，区别在于视线不一定是水平视线。这种方法常在测量跨度较大或高程测量精度要求不高的情况下代替水准测量。如图2所示，利用将全站仪架设在已知点和未知点中间，利用仪器测得的角度和距离推算已知点和未知点之间的高差，从而计算得到未知点的高程，这一方法的特点决定了它相对于一般三角高程测量方法具有如下优势：

首先，它避免了量取仪器高这一环节，消除了高度量取所带来的误差，这一点至关重要，因为仪器高的量取一般通过钢尺量取，精度只能达到毫米级，极大地影响了测量精度。

其次，把仪器架设在已知和未知点中间，前视和后视距离基本相等，可抵消地球曲率的影响，同时，消弱大气折光和仪器照准误差的影响。

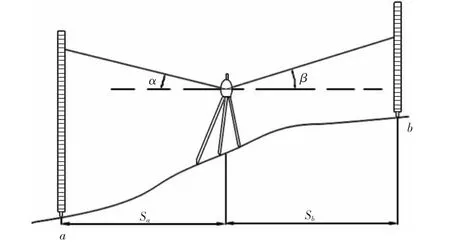
图2 中间法三角高程测量示意图

3.2 应用背景

“徐汇区156号地块项目”位于上海市徐汇区番禺路以东、虹桥路以南、徐虹北路以西、南丹路以北，该工程建成后是集办公、商业及居住为一体的商办、商住建筑群，基坑开挖深度9.60 m～11.00 m，项目周边环境复杂，有较为密集的市政管线和高层建筑，基坑开挖顺序为顺作法结合逆作法施工，为尽早形成支撑体系，以减少基坑开挖初期的变形，基坑围护形式为钻孔灌注桩+三轴搅拌桩+两道钢支撑。顺作部分主要有8#房基坑、6#房基坑、3#、5#房基坑、1#、2#房基坑，均为两道钢支撑，基坑安全等级一级，根据该基坑安全等级、环境等级及地基复杂程度，该工程监测等级为一级[3]。

项目首先组织开挖8#房基坑，在施工过程中，钢支撑受压严重，导致其连接螺栓蹦落，引起项目各参与方的广泛重视。经分析，主要原因为施工未按照施工组织设计分层开挖，同时要求监测单位加强钢支撑轴力的同时，对立柱隆沉进行监测，以掌握其隆沉变形对支撑稳定产生的影响。但是，因该项目采取的钢支撑未采取防护措施，测量人员无法从钢支撑走到立柱部位进行水准测量。对此，项目业主方要求施工单位在今后的施工中必须设置防护措施。在1#、2#房土方开挖时，因种种原因施工单位又未设置防护措施。在此情况下，监测人员采用了“中间法三角高程”的方法对立柱隆沉进行监测。

3.3 方法及误差分析

中间法三角高程测量主要方式方法如图3所示。

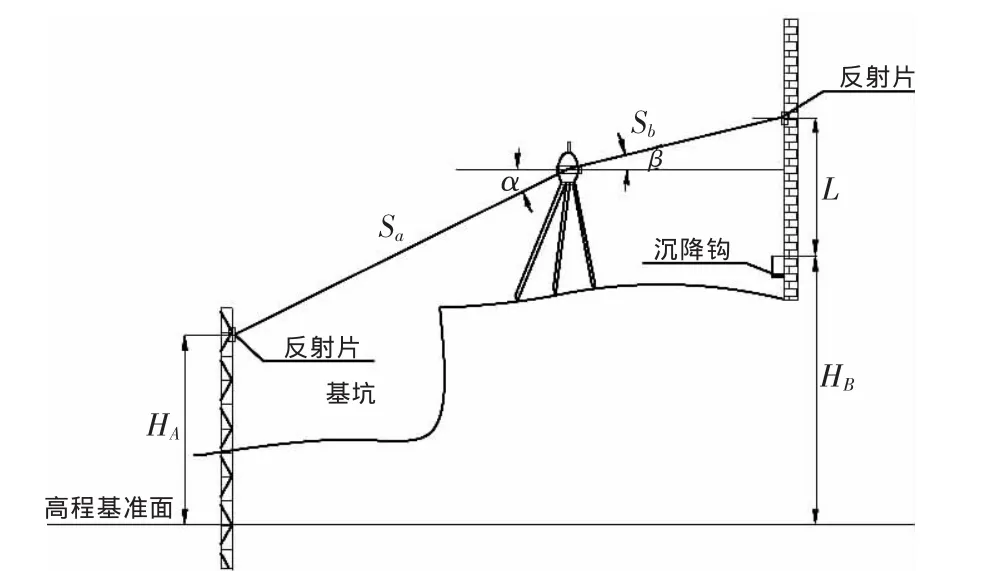
图3 中间法三角高程测量原理图

在基坑周边的建（构）筑物上布设沉降钩，纳入沉降监测网，按照一等水准执行。在沉降钩对应的适当高度，布设反射片作为三角高程测量的后视点，该反光贴和沉降钩的高差为固定值（L）。在需要的监测的立柱上选择合适位置，也布设反射片作为三角高程测量的前视。仪器架设在立柱和建（构）筑物中间的基坑边，用以测量两者之间的高差来推算立柱的隆沉。

从图3可知：

不考虑地球曲率和大气折射的影响，监测点A的高程计算见公式（4）：

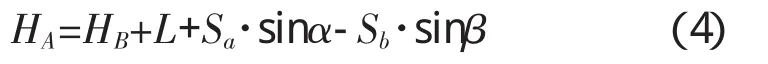
考虑地球曲率和大气折射的影响，监测点A的高程计算公式见公式（5）：

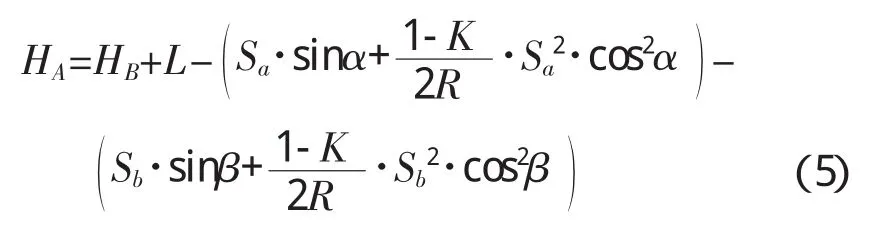
从公式（4）、（5）可见，此方法避免了通过钢尺量取仪器及棱镜高，消除了这部分误差源，A点高程测量精度只受后视点B高程测量精度、仪器测量精度、大气折光和地球曲率、照准误差的影响。

同时，通过选择合适的站点，来控制前后视距差，可以抵消一部分地球曲率的影响，所以，两侧的视距越接近，测量效果越好。

测出的结果从理论上分析比传统的三角高程测量精度更高，它减少了误差来源，整个过程不必量取仪器高和棱镜高，减少了误差源。从基坑监测的特点来看，因基坑面积一般在一定范围内，全站仪测量距离也就局限在一定长度。同时，在立柱顶布设监测点使得仪器中心点与监测点的高差较小，这方面的特点在三角高程中可以减小大气折光和地球曲率的影响。

参照公式（3）可知监测点A的高程测量误差为：

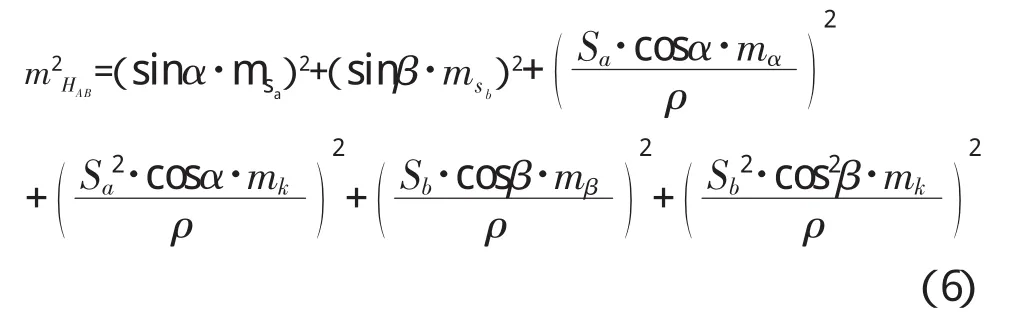
已知 mα=mβ，再假设 Sa=Sb、α=β，式（6）可写成：

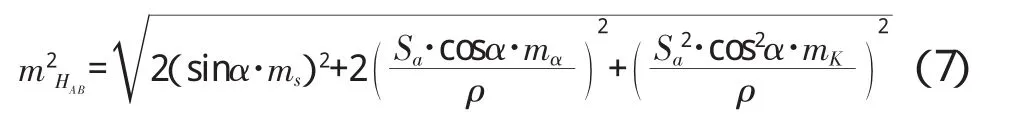
在实际观测中，人们采用的仪器是徕卡TCA2003，测距精度1 mm+1 ppm，测角中误差0.5”，mK取土 0 ．04 mm[4]，代入式（7）计算高程中误差，计算结果如表1所列。

可见，在1 000 m距离范围内，竖直角不超过20°的情况下，高差中误差测量的精度一般在0.5 mm以内，可以达到二等水准的精度要求。

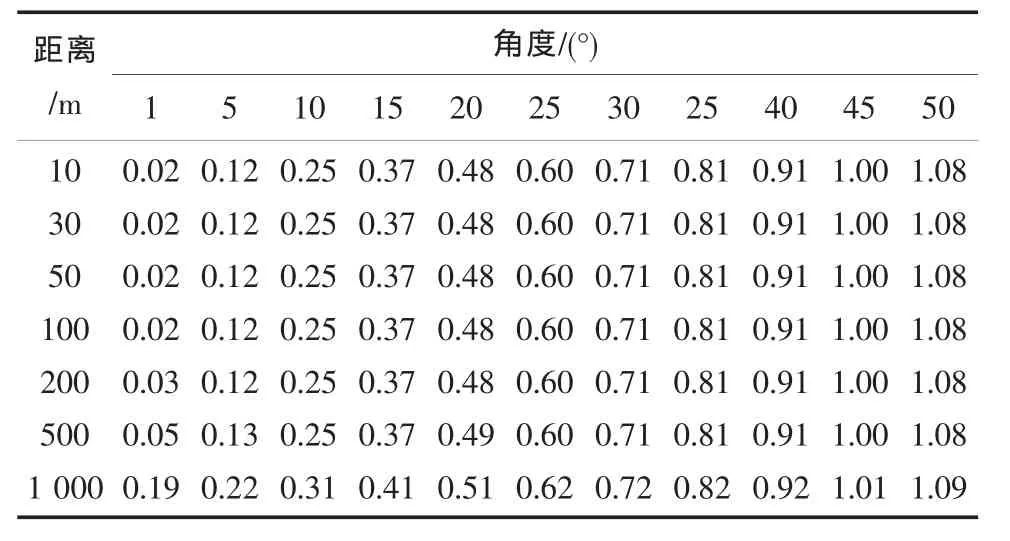
表1 不同角度和距离的误差分析一览表

且在测量过程中可自动计算悬高，即S·asinα和S·bsinβ，使得测量工作更加直观便捷。在项目实施过程中，以1#、2#房基坑的立柱监测为例，见图4所示。

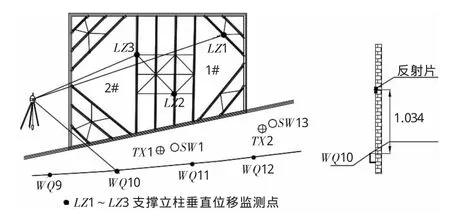
图4 布点图

在监测过程中，因受通视条件影响，单站只监测了LZ1、LZ3两点的监测数据，因围墙沉降监测点WQ10紧邻基坑，且纳入了一等水准网，在基坑开挖期间每天监测一次。其他基础施工期间3d监测一次，所以，即便它受施工影响较大，基坑开挖后势必有较大沉降，但是因监测频率较高，成果更新速度较快，可以选择它作为后视去监测立柱隆沉。在WQ10监测点的上方布设反光贴，利用钢尺量得高差为1.034 m。在基坑开挖前，在立柱上通视较好的部位布设反光贴作为监测点，后续监测过程中无须再靠近立柱。站点选择要尽量保证前后视距相等，且要保证照准目标时，竖直角不超过20°。按式（4）计算可知在基坑从土方开挖至地下结构施工至±0期间L1、LZ3的累计垂直位移变形量如表2所列。

根据表2绘制变形曲线，见图5所示，由图5可见，立柱上抬明显，而且位于基坑中心部位的LZ3明显比LZ2上抬量大，与基坑坑底变形的特点相符。

在土方开挖初期，立柱隆起速率较快，平均达到3mm/d。对此，作为监测单位及时将此情况反馈给项目各参与方，总包单位安排专业支护分包单位加强支撑连接情况的检查，并要求挖土单位降低挖土速度，逐层开挖，随着基坑底板浇筑完毕，立柱隆起的变形速率逐步减小，最终保证了整个基坑工程顺利施工至±0。

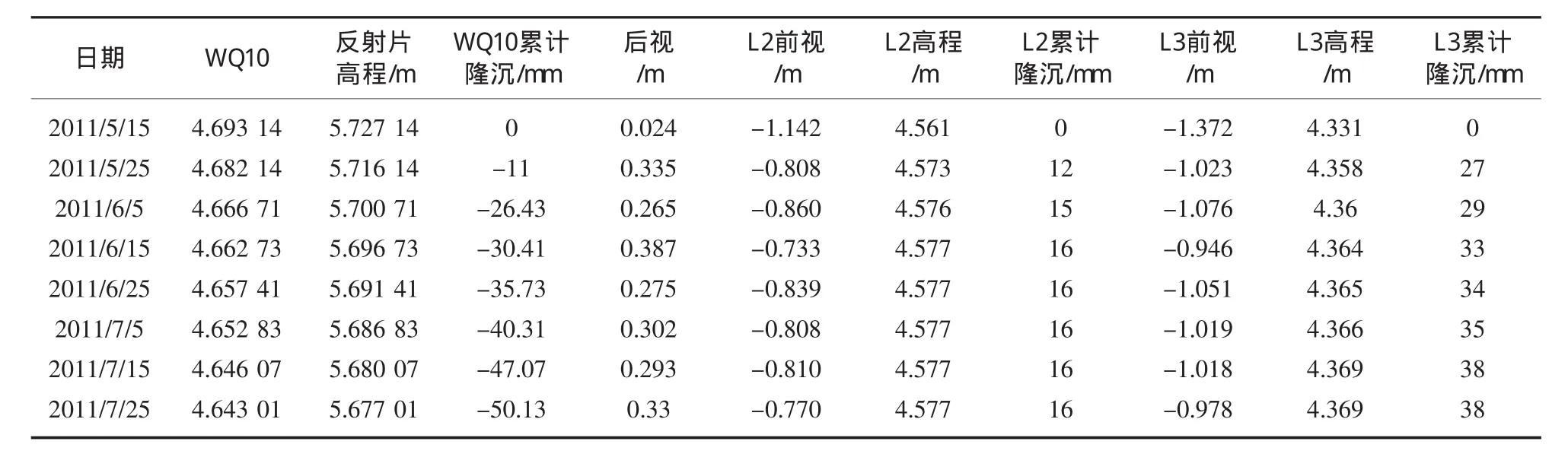
表2 计算结果一览表

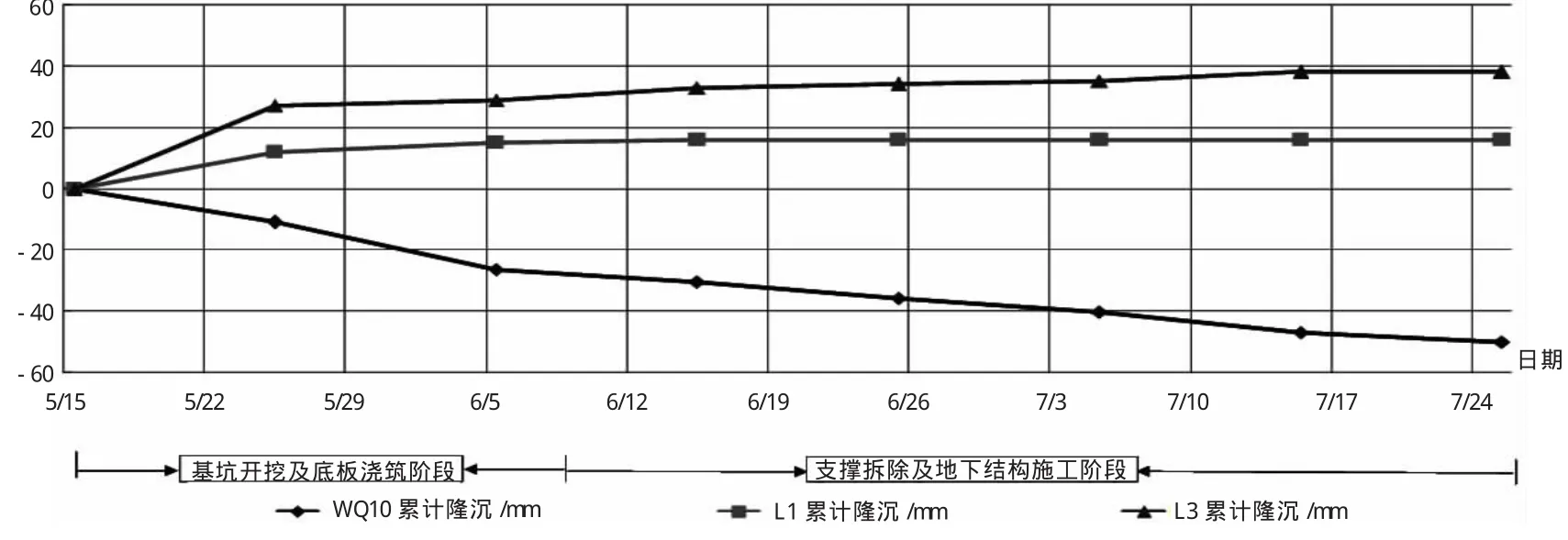
图5 LZ1、LZ3立柱隆沉曲线图

4 结语

通过理论计算和工程实例可见，通过中间法三角高程测量，不用量取仪器高及棱镜高的方法，减少了测量过程中的误差源，在竖直角小于20°，同时，利用基坑变形监测的特点，将其他误差影响因素控制在一定范围内，可以有效地、较精确地获取立柱在竖直方向的变形量，可以达到二等水准的精度要求，解决了实际工作中无法靠近立柱点进行常规水准测量的难题。

[1] 武汉大学测绘学院测量平差学科组． 误差理论与测量平差基础（第2版）[M]．武汉：武汉大学出版社，2009.

[2] 武汉测绘科技大学《测量学》编写组．测量学（第3版）[M]．北京：测绘出版社，1991.

[3] DG/TJ 08-2001-2006，基坑工程施工监测规程[S]．

[4] 刘丽霞，乔万亮，佟艳丽．利用全站仪进行三角高程测量的中误差计算[D]．黑龙江水专学报，2005：59-60．