单排管温度场经典公式的修正研究

施振东

（中铁十六局集团有限公司北京轨道交通工程建设有限公司，北京市 101100)

0 引言

在城市地铁规划设计中，上下行隧道之间通常设置联络通道。联络通道施工时，不仅需要考虑自身结构的稳定和地面建构筑物的安全，而且要确保主隧道的稳定，联络通道的安全防护系数远远不如主隧道完备。因此，联络通道施工时通常要对施工区域土体进行加固处理，以保证施工的安全及减小对周围环境的影响。冻结法是在地层中按预定间隔埋设冻结管，通过其中的冷却液循环，使管周围地层中的孔隙水以管为中心生成年轮形柱状图。近年来，随着城市地下轨道交通的迅猛发展，冻结法工艺已被广泛应用于上海、北京、深圳、杭州等城市地铁工程施工中。

单排管冻结是目前应用较多且理论研究比较成熟的方法，美国学者Sanger&Sayles基于经验给出了单排管冻土帷幕温度场的简化计算方法，并在实际工程中得到一定的应用。但该经典公式没有考虑温度沿轴面上的变化，使其计算结果与实际工程存在较大误差。

采用ANSYS软件分析了单排管温度场的分布规律，分析了Sanger&Sayles经典公式的主要缺陷并进行了修正，使其能考虑温度沿轴面上的变化。

1 Sanger&Sayles经典公式简介

Sanger&Sayles经典公式将单排管温度场的发展分为两个阶段（见图1）：第一阶段是冻土柱围绕单独的冻结管发展；第二阶段是冻土柱交圈并随时间冻土墙不断发展变厚。同时，假定第一阶段温度在冻结区和未冻区上成对数曲线发展；第二阶段温度在冻结区成直线分布，在未冻结区呈对数曲线分布（见图2），并且给出了各个阶段温度场表达式。

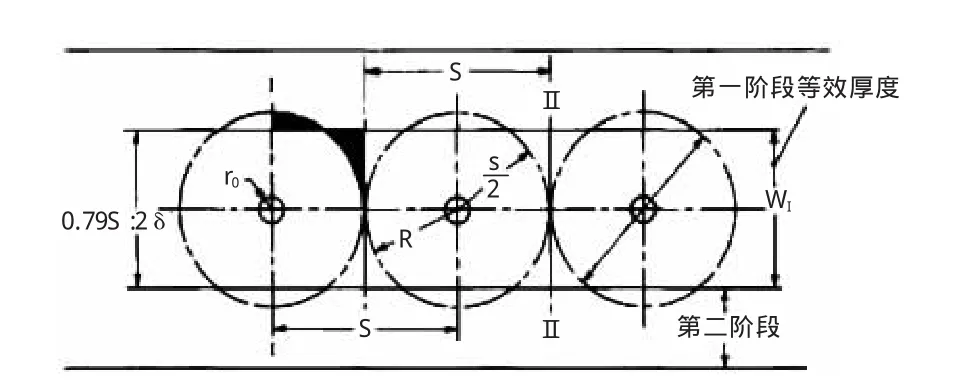
图1 Sanger&Sayles单排管模型温度场计算简化图

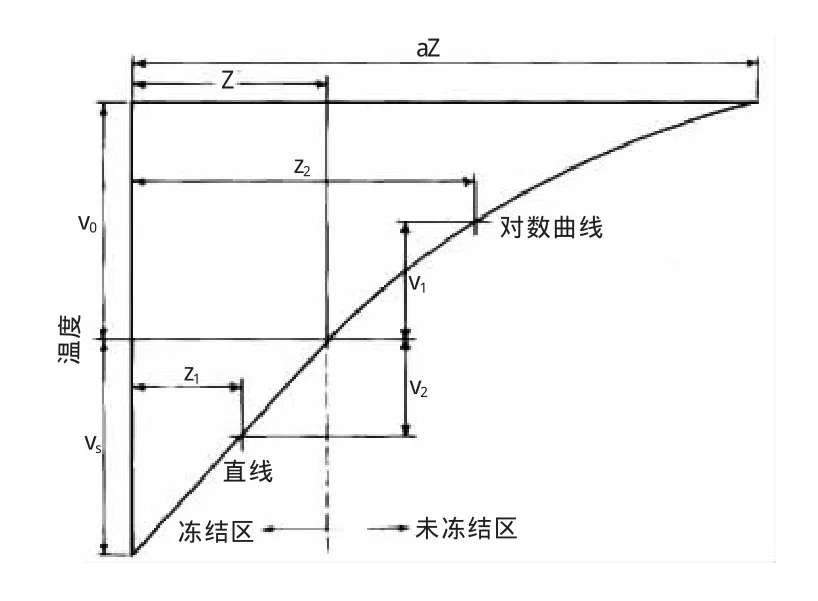
图2 Sanger&Sayles单排管模型温度分布曲线图

在图2中，vs是冻结管温度与水的冰点温度之差，计算中取绝对值；v0是土体初始温度与水的冰点温度之差，计算中取绝对值；Z是冻土与未冻土的分界线与冻结管轴线之间的距离，即单侧冻土厚度；v1是距离冻结管中心距离为z1处的土体温度；v2是距离冻结管中心距离为z2处的土体温度；a（ar）是冻结影响范围系数，一般取4.5到5，建议取5，对数曲线的表达式如式（1）所列：

Sanger&Sayles公式认为冻土几何交圈时，冻土柱体单侧冻土厚度为：δ=0.79S/2（S为冻结管间距），如图2所示；在几何交圈以后采用式（1）和图2来计算单排冻结管温度场分布。

2 单排管冻土温度场数值模拟

大型通用有限元软件ANSYS在热力学计算方面可以清晰、直观地反映冻结壁温度场情况，与工程监测结果比较符合，所以本文采用ANSYS软件作为数值分析工具。

温度场分布是随时间变化的，且冻土帷幕的厚度也是随时间逐渐发展的。为全面了解温度场的时空规律，采用瞬态导热模型分析单排管的二维温度场。模型及参数的选取如下：

（1）单元采用2维4节点热实体单元plane55。

（2）土体的材料如表1所列。

表1 土体计算参数表

（3）土体初始温度为18℃，冻结管表面施加随时间变化的荷载（10 d降到-26℃；15 d降到-30℃）。

（4）为了充分考虑冻结法的温度影响空间，设定模型大小为：在沿冻结管布置方向上为[（n-1）×l+10]m，在垂直方向为10 m，冻结管管径为0.108 m。其中，n为冻结管个数，l为冻结管轴心间距。

冻结管间距为1.0m时的有限元模型的网格划分及最后时间步的温度场分布如图3、图4所示。

图3 有限元计算网格示意图

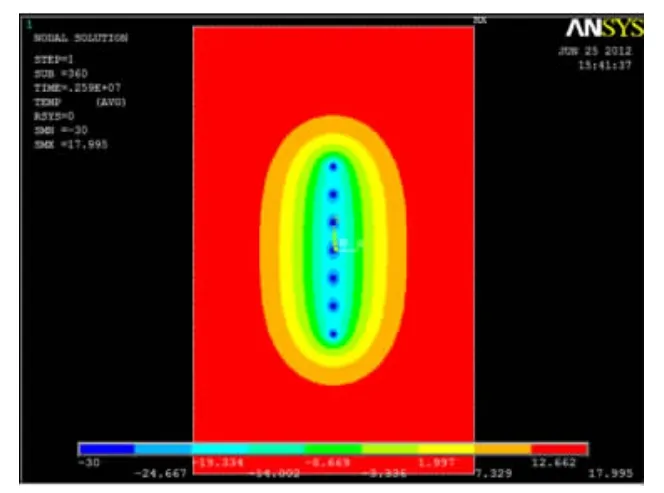
图4 冻结30 d时温度场分布示意图

3 Sanger&Sayles经典公式的缺陷

在实际工程中，冻结管的间距一般在0.5 m～1.5 m；冻土帷幕相对厚度采用表示（ξ为主面单侧的最大冻土厚度；l为冻结管间距），其值一般控制在0.5～1.5。为了较好地验证Sanger&Sayles公式，分别设置冻结管间距为0.5 m，1.0 m，1.5 m，分别考察其在不同冻结厚度时的温度分布，并与Sanger&Sayles公式计算结果对比分析，整理成如图5所示。

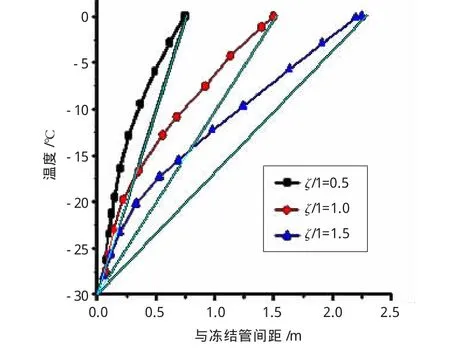
图5 l=1.5时主面温度数值计算结果与公式对比曲线图

从l=1.5时数值计算的结果可知，单排管冻土温度场在主面上的温度分布曲线不同，与实际不符。对比数值计算结果和公式结果可知，随着冻结厚度的增大，冻结区的温度差别逐渐减少；在主面上公式的误差小于界面误差。因此，垂直于轴面方向的温度场可以近似采用线性拟合，其误差在工程允许范围内。

4 Sanger&Sayles经典公式的修正

基于上述对比分析结果，对Sanger&Sayles公式冻结区域部分进行修正，对t0、l0的函数形式推导如下。

（1）t0的形式假定如式（2）所列：

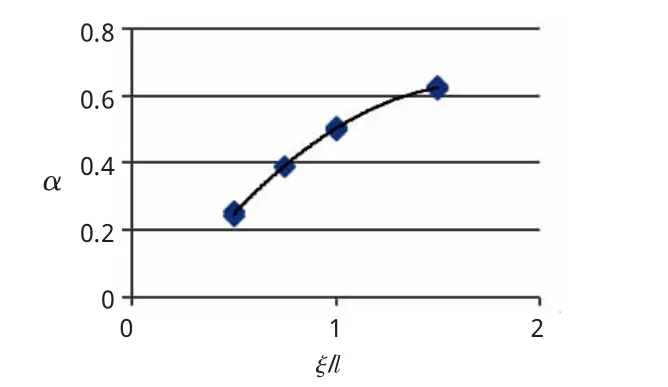
图6 α与ξ/l近似关系曲线图（l=1.5 m）

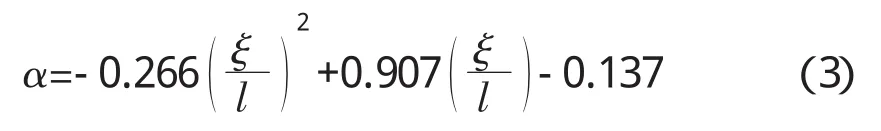
假定 β 与l近似成线性，以1.5 m的冻结管间距为基准，拟合线性关系如式（4）所列：

（2）l0的形式假定如式（5）所列：

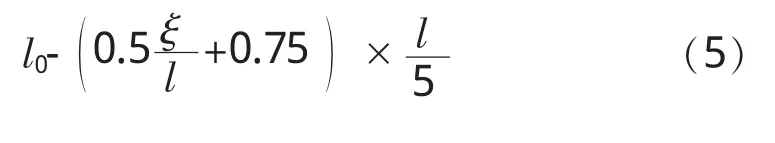
5 Sanger&Sayles修正公式的验证

表2 不同工况计算结果表

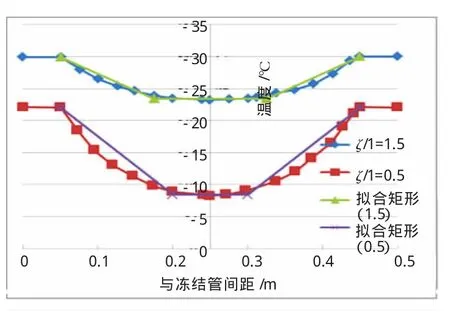
图7 温度沿轴面变化曲线图（l=0.5 m）

由此可见，修正的Sanger&Sayles公式能够较好地反映温度沿轴面方向的变化，克服了原有公式假定温度沿轴面不变的缺陷。这种修正能够更真实地反映实际的温度场，并且形式简单，方便计算整个冻结场的平均温度。

6 Sanger&Sayles修正公式的平均温度计算方法

修正的Sanger&Sayles公式假定温度场沿轴面方向呈现梯形分布，而在垂直于轴线方向冻结区域内呈现直线分布，因此当采用修正的Sanger&Sayles公式计算人工冻土温度场是不涉及积分，只涉及简单的运算，方法简单方便。

人工冻结场的平均温度的简化公式为：

表3 平均温度计算结果汇总表

7 结论

本文分析了Sanger&Sayles经典公式的不足和缺陷，然后对其进行修正。总结如下:Sanger&Sayles经典公式假定温度沿轴面方向为定值，是产生Sanger&Sayles公式计算结果存在较大的误差的主要原因。修正的Sanger&Sayles公式假定在冻结区区域，沿轴面方向上为梯形分布，垂直于轴面方向上为直线分布。修正的Sanger&Sayles公式能够较好地反映实际的冻结温度分布。

[1] 陈文豹,汤志斌.潘集矿区冻结壁平均温度及冻结孔布置圈径的探讨[J]．煤炭学报，1982，(1)：46-52．

[2] Sanger F J,Sayles F.H.Thermal and rheological computations forartificially frozen ground construction[J].Engineering Geology,1979,13(1-4):311-337.

[3] 刘瑞锋,胡向东,皮爱如.人工二次冻融土热力学参数试验[J].煤炭学报,2008,33(5):518-521.

[4] 杨波,丁文其,胡向东,等.单排管冻土帷幕平均温度控制参数敏感性分析[J].地下空间与工程学报,2012.