古塔观测数据的计算和变形分析

付小娟 吴洪坤

(1.广州民航职业技术学院 人文社科学院，广东 510403;2.广州民航职业技术学院 飞机维修工程学院，广东 510403)

1 引言

某古塔已经有上千年历史，是我国重点保护文物。但由于古塔长时间承受自重、气温、风力等各种作用，偶然还要受地震、飓风的影响，古塔会产生各种变形，诸如倾斜、弯曲、扭曲等。为保护古塔，文物部门适时对古塔进行观测，每次都得到一组数据，以制定必要的保护措施。现根据2013 年全国大学生数学建模竞赛C 题附录1 的数据，提出确定古塔各层中心位置的通用方法，并列表给出各次测量的古塔各层中心坐标。分析该塔倾斜、弯曲、扭曲等变形情况。

2 建立模型

2.1 问题分析

古塔在倾斜、弯曲、扭曲等变形中，每一层的层面结构、塔心坐标等都发生了变化，为方便起见，首先只计算各次测量的第一层塔心，把每次测量得到的第一层的测试点作为研究对象，并且按照题目给出的顺序编号为1，2，3.....8 号点，为了解八个点的相对位置，利用matlab 画出四次测试第一层八个点的空间图形，如图1 所示，发现测试点不在一个水平面上，组成一个类似于八边形的结构，经计算八条连线的长度如表1 所示，每条连线是不等长的，所以测试点并不是均匀取定的，但是前两次测试的数据比较接近，各条连线对应几乎相等，后两次测试的数据也比较接近，各条连线也对应几乎相等，由此推断，前两次测试点是一一对应的，而后两次测试点也是一一对应的。

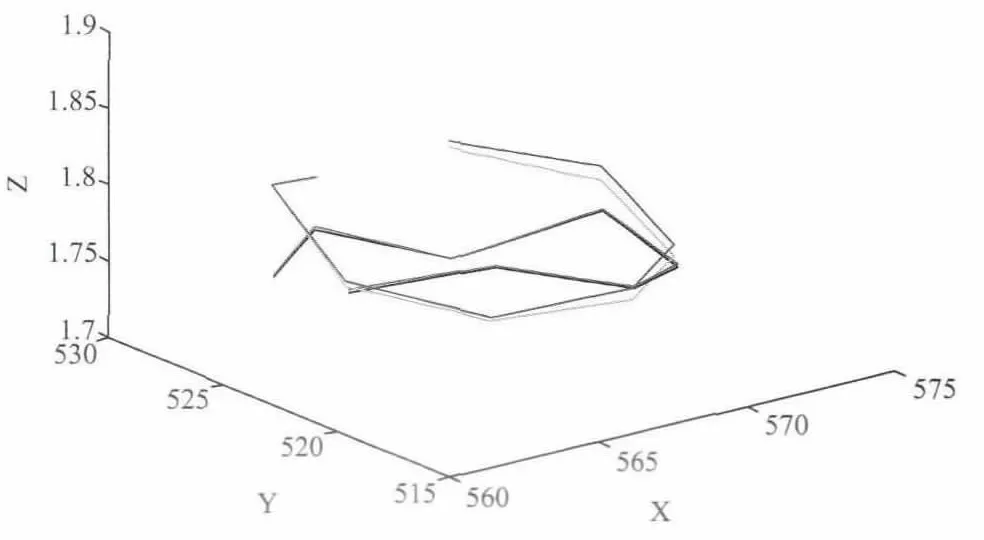
图1 第一层坐标图.蓝:1986，绿:1996，红:2009，黑:2011

为了组成一个平面多边形，设想把测试点投影到某个平面上，用投影八边形的重心坐标表示塔心坐标，由于各次测试点并不在一个水平面上，所以采用空间倾斜平面作为投影面，首先利用各层八个测试点拟合一个空间平面，如图2 表示1986 年测试第一层八个测试点拟合的空间平面，然后把测试点投影到这个空间平面上，这样就可以得到一个空间平面上的八边形［1］，利用matlab 求得八边形的重心，就得到了各层的塔心坐标。

根据问题一求出的四组塔心的坐标，算出顶层与底层的倾斜位移，进而求出倾斜量。再用各次测量每一层的塔心坐标拟合出四条空间曲线，用曲线的曲率表示塔的弯曲情况。塔的扭曲度可以利用同一个测试点相对于塔心发生的扭转来描述。通过前面变形数据的分析，可以得到塔在以后的变形趋势。根据塔的变形趋势，我们提出了几点建议。

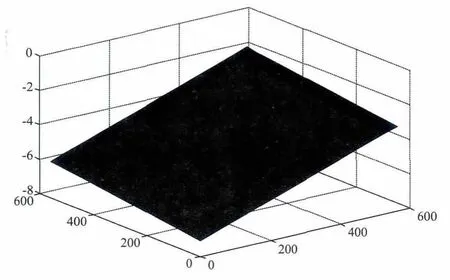
图2 1986 年测试第一层坐标点拟合的空间平面图

2.2 模型建立

2.2.1 塔心坐标模型的建立与求解

图1 所示第一层的八个测试点不在一个水平面上，把1986 年测得的原始数据绘成图3，发现形如塔状，其他各层测试点也不在一个水平面上;所以采用先根据测试点拟合一个空间平面Π，Π 的方程常用公式(1)表示，当有n 个测试点时，要拟合这个平面，可以表示成矩阵［2］方程(2)的形式，利用matlab［3］求解出各层测试点拟合的平面方程，把每次测的各测试点投影到这个拟合平面上，设空间中任意一个点是B1(x1，y1，z1)，其在平面Π 上的投影点设为B2(x2，y2，z2)，则投影方程如公式(3)所示，算出k 值，带入(3)式得到各个测试点的投影点坐标，连成投影八边形，求其重心坐标。

多边形的重心计算［4］，设有图4 所示的n 边形A1A2…Ai…An，各顶点坐标分别是Ai(xi，yi，zi)(i=1，2...n)，连接AnA2，AnA3，…AnAi，…，AnAn-2，得到n-2 个三角形，设各个三角形的重心坐标分别是Gi()(i=1，2...n -2)，其中每个坐标的计算如公式(4)所示。

设第i 个三角形的面积是σi，先利用两点之间距离公式，求出第i 个三角形的三边长ai，bi，ci，再套入公式(5)求出σi。设多边形的重心坐标为O ()，计算公式如公式(6)所示。

表1 四次测试第一层八个测试点之间的距离

由公式(1)到(6)，利用matlab 算出第一、七、十三和塔尖的塔心坐标，如表2 所示。

图3 1986 年测试各层测试点空间图

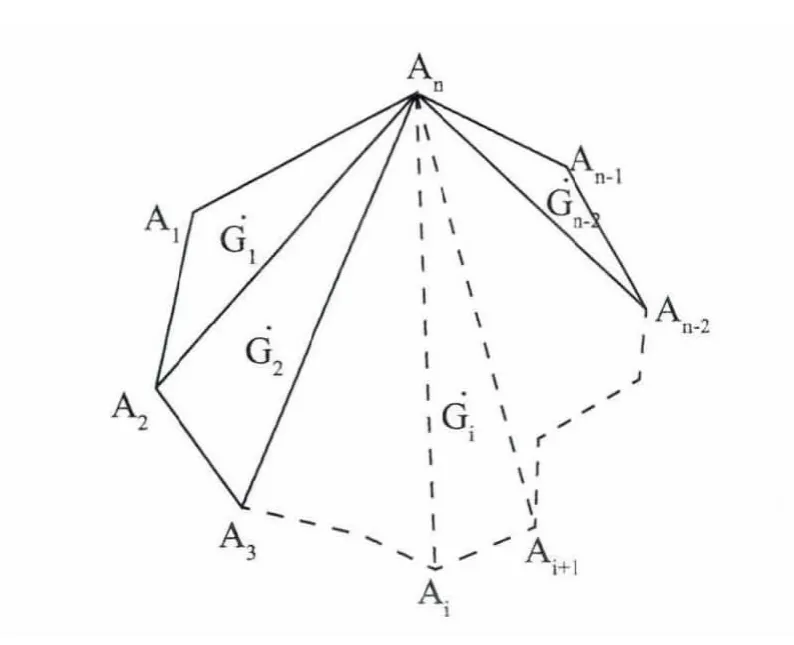
图4 平面多边形重心坐标的计算

表2 中数据与测试的原始数据比较吻合，非常接近各层测试值，1986 年和1996 年的测试数据及计算数据都更接近，说明前两次的测试点是一一对应的，而且这10 年间，古塔变形情况比较小，维护较好;而2009 年和2011 年的数据更加接近，这说明后两次的测试点也是一一对应的，说明这期间的维护比较频繁，古塔变形较小;但是从1996 年到2009 年这15 年间，发现古塔的变形比较大，同一层的塔心横坐标x 的变化范围是(0 -0.4961)m，纵坐标y 的变化范围是(0 -0.6551)m，竖坐标的变化范围是(0 -0.0146)m。同一层塔心的横坐标值越来越大，说明古塔的倾斜朝着x 轴的正方向;纵坐标的变化规律比较复杂，这和古塔的扭曲变形严密相关;同一层塔心的竖坐标z 的值随着时间的推移变得越来越小，这表明了古塔的实际弯曲变形。

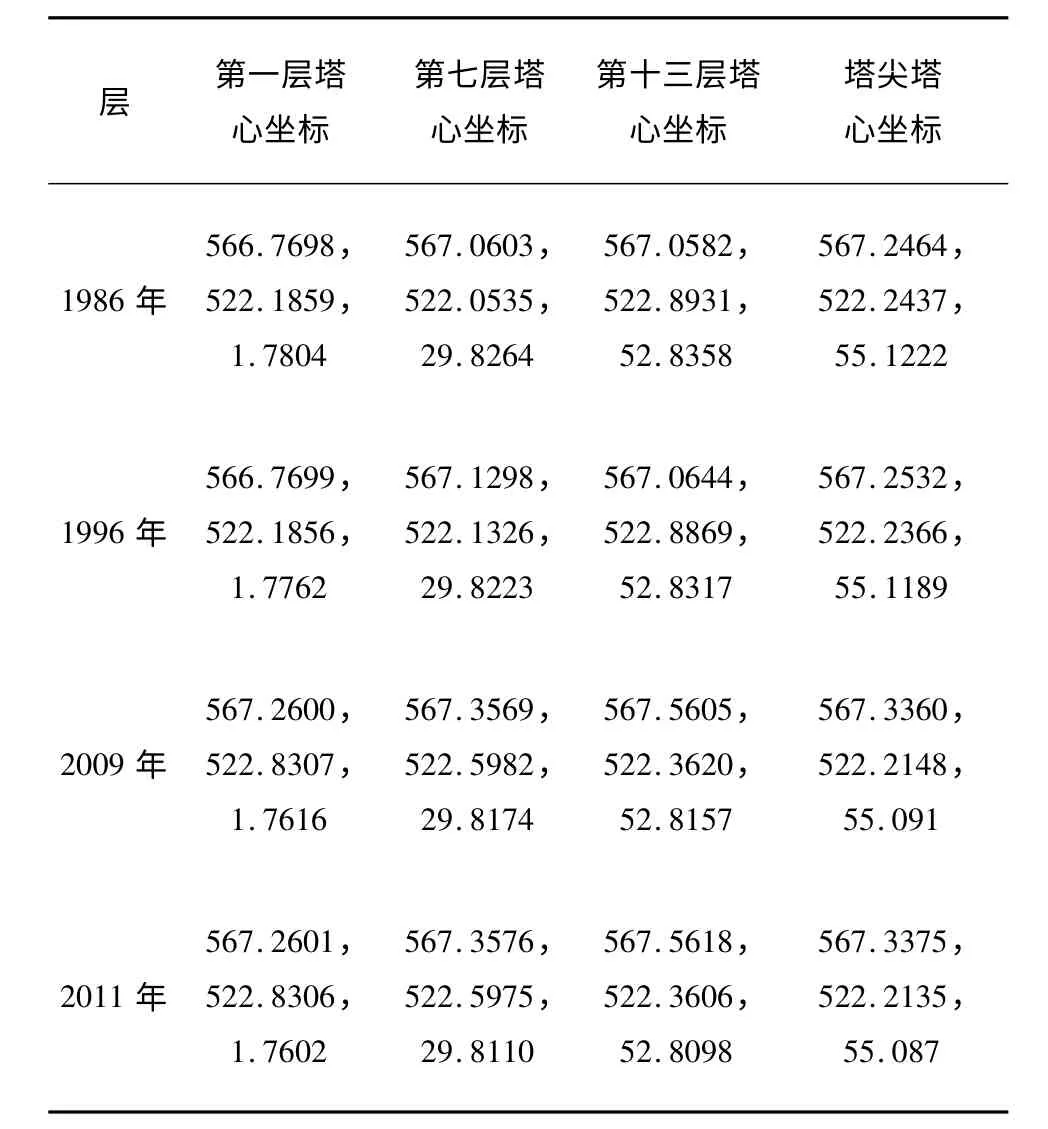
表2 四次测试各层的塔心坐标

2.2.2 塔的倾斜度模型

塔的倾斜是由于基础立柱顶面高低不平而引起塔中心偏离铅垂线位置的现象，采用顶层塔心相对于底层塔心的水平位移变化来刻画古塔的倾斜［2］［5］。设古塔第一层的塔心坐标为(x1，y1，z1)，顶层的塔心坐标为 (x14，y14，z14)，塔底到塔顶塔心的高度为H，则倾斜位移δ 如公式(7)所示，倾斜度β 如公式(8)。计算结果如表3所示。

该古塔的倾斜度随着时间的推移越来越大，查询数据资料可得当倾斜度小于0.004 是正常允许的，但是表四中数据都大于0.004，所以该古塔需要尽快进行修缮，在倾斜方向加固立柱。

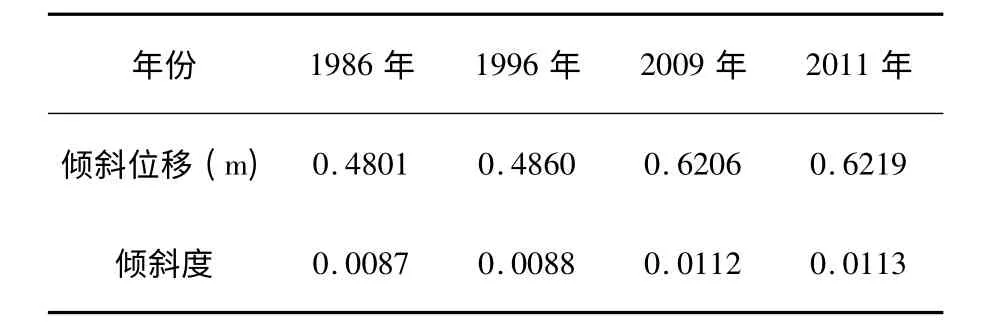
表3 国外主流BIM 服务器对比

2.2.3 塔的弯曲度模型

把同一年的13 个塔心坐标拟合出一条空间曲线，共可以拟合出四条曲线如图5 所示。塔的弯曲度可以利用各层塔心坐标连线的曲率来刻画，因此，先把各层塔心坐标分别投影到XOZ 面(图6)和YOZ 面上(图7)，利用投影点拟合成一个圆(9)，因为有多个塔心，所以把圆方程写成矩阵方程(10)

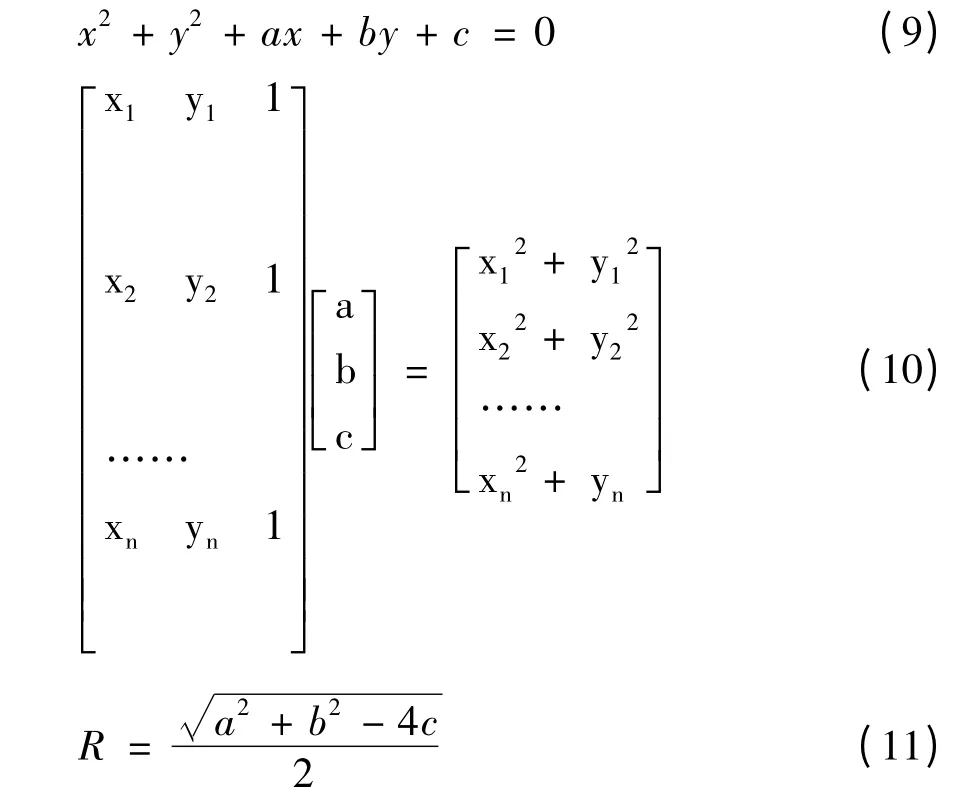
利用matlab 计算出a，b，c，由此找到半径R如公式(11)，曲率ρ=1/R。由此可以计算出曲线在X=0 和Y=0 两个投影面上的综合曲率(如表4)。发现1986 年和1996 年弯曲度基本相同，2009 年和2011 年也相同，塔朝着x 轴正方向的的弯曲度从1996 年到2011 年有很大递减，而朝着y 轴负方向的弯曲度却有所递增，说明在这期间对塔的弯曲变形采取了一定保护措施，使之逐渐回归直立的状态。

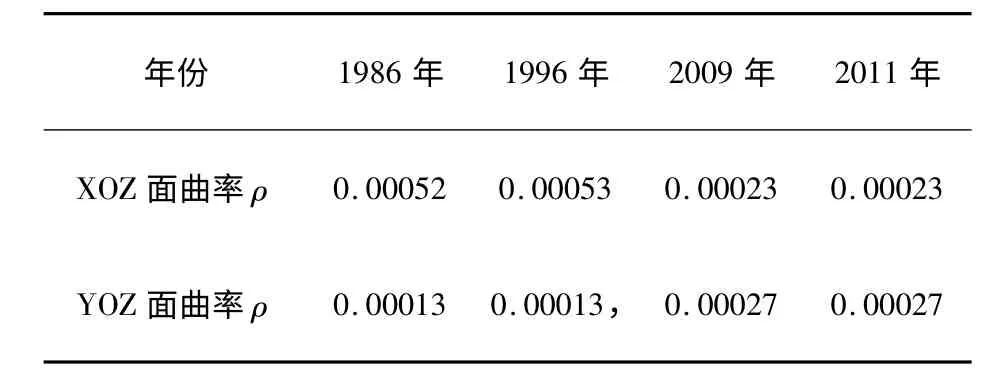
表4 古塔弯曲的曲率年份

2.2.4 塔的扭曲度

平面的扭曲变形定义为“所考虑平面的两个对边旋转角度之差随其距离的变化率”来描述【6】。采用同一个测试点与塔心连线发生的扭转角度来计算塔的扭曲度，根据前边证明1986年和1996 年的测试点是一一对应的，设1986年第一层塔心坐标为O，第i 次测量第一层的第j 个测试点为Aij，连接，求出两条线之间的夹角，然后求另外七对测试点与O 点连线的夹角，……，，算出八个夹角的平均值，表示古塔第一层从1986 年到1996 年所发生的扭曲度，同理可求其他扭曲度，篇幅所限，本文不做计算。

图5 各层塔心拟合空间曲线

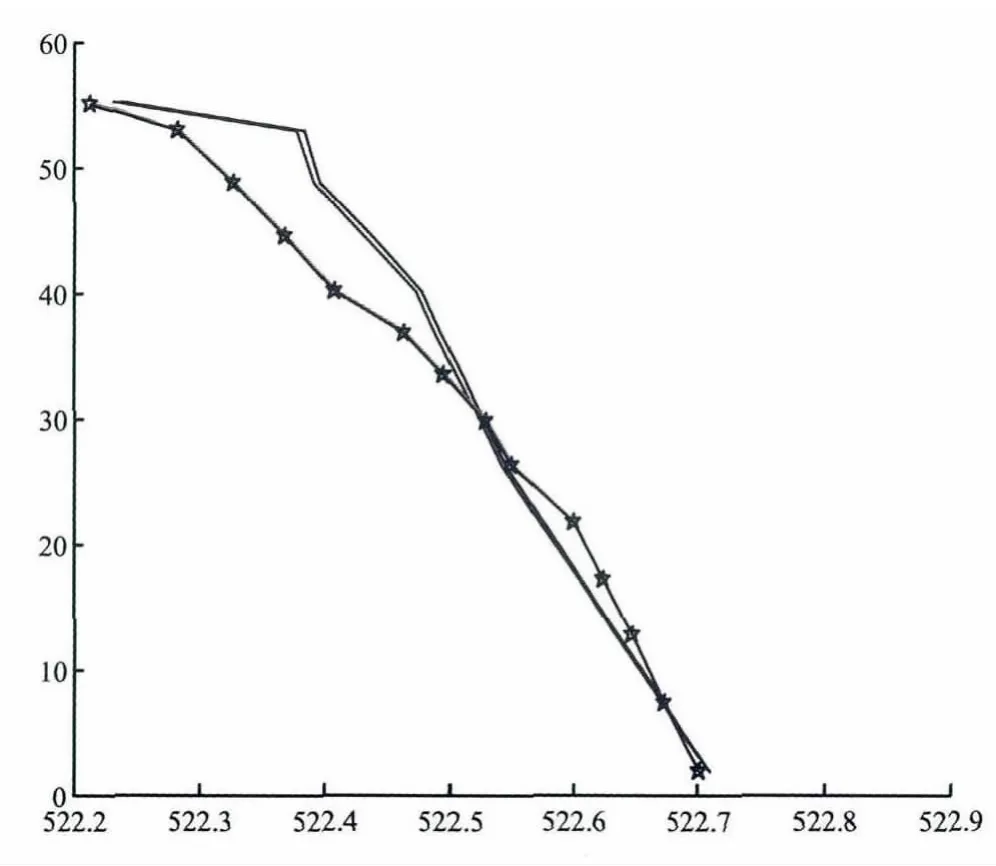
图6 塔心在XOZ 面投影曲线图

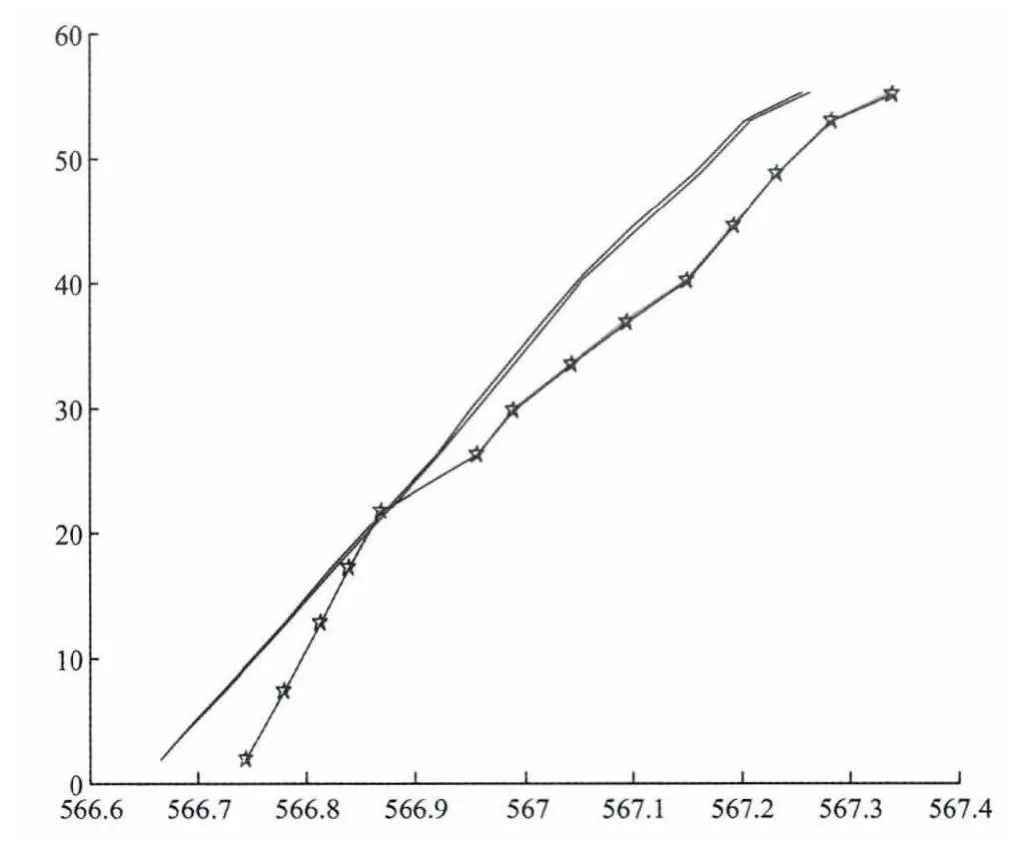
图7 塔心在YOZ 面投影曲线

3 结论

该古塔的倾斜变形比较严重，而且逐年增长，建议今后加强倾斜检测与防护;弯曲变形比较小，说明在弯曲防护方面做得比较好。古塔监测内容的实施以及频率按各塔的健康程度和委托方的要求而定，监测周期根据现场实际情况可适当调整，建议今后每隔3 -4 年进行一次古塔平面和高程的监测，如发现周边建筑或者地铁等施工，地质状况发生剧烈变化，可进行加密测量，以便监测出古塔随时间的变化产生变形量，从而保证对古塔的安全维护提供最新最可靠的数据和更好地进行古塔保护。

［1］黄强.古塔变形监测的探讨［J］.测绘与空间地理信息，2013，36(6):217 -220.

［2］胡志晓.古塔倾斜观测和数据分析［J］.江苏建筑，2011(6):34-36.

［3］周博，谢东来等.MATLAB 科学计算［M］.北京，机械工业出版社.

［4］郭幼操.从四边形重心到多边形的重心［J］.浙仁农村技术师专学报，1996(1-2):30-33.

［5］余周佑.安庆振风塔倾斜测量与数据分析［J］.施工技术研究与应用，2003(5):34.

［6］韩煊，Jamie R Standing，李宁.地铁施工引起的建筑物扭曲变形分析［J］.土木工程学报，2010，43(1):82-88.