基于Excel的间接平差坐标转换与实现

刘洪晓 张国君

（招金矿业股份有限公司河东金矿，山东 招远265402）

0 引入

在利用手工数字化仪采集GIS数据中，往往由于数字化仪坐标系与地面坐标系不一致及图纸变形而产生系统误差，为了消除此误差，通常是根据已知地面坐标的控制点和格网点采用平面相似变换法进行处理。在本文中，笔者基于Excel实现了坐标转换的过程。

1 原理

为进行平面坐标转换，需要有一定数量的公共控制点，这些公共点应具有两个坐标系中的双重坐标。

已知新旧坐标系的坐标变换方程为：

式中m为尺度比因子，α为旋转因子。

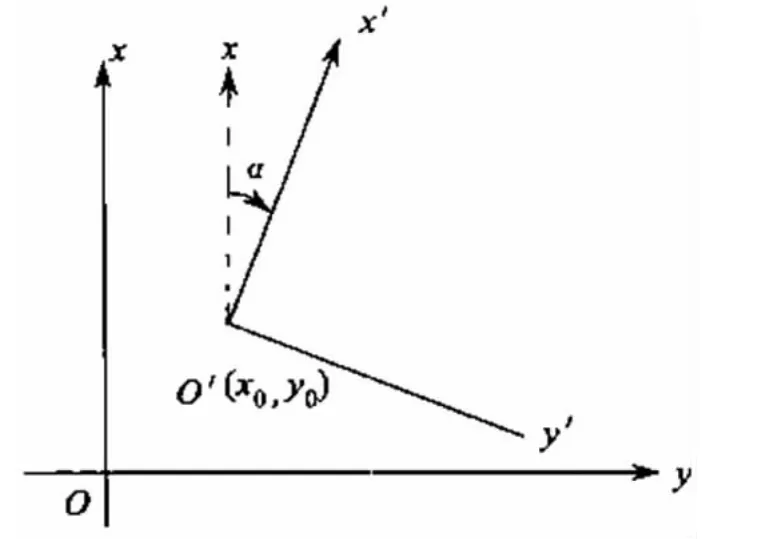
图1 坐标转换示意图

如图 1 所示，令 a=x0，b=y0，c＝mcosα，d＝msinα，则（1）式可写成：

式中a、b、c、d为所求的未知量，即平差参数。

设两坐标系中有 n 个公共点（xi,yi）和（xi′,yi′），i＝1,2,…,n，令新坐标系的坐标为观测值，旧坐标系中坐标设为无误差，当n＞3时，则可列出误差方程为：

2 基于Excel的过程实现

2.1 已知坐标数据

如图2所示，在Excel中输入已知点号为1、2、…、7的点在新、旧坐标系中的数据：

图2 输入已知数据

2.2 列立误差方程

依据式（3），取n＝7，则如图3所示，误差方程式如下

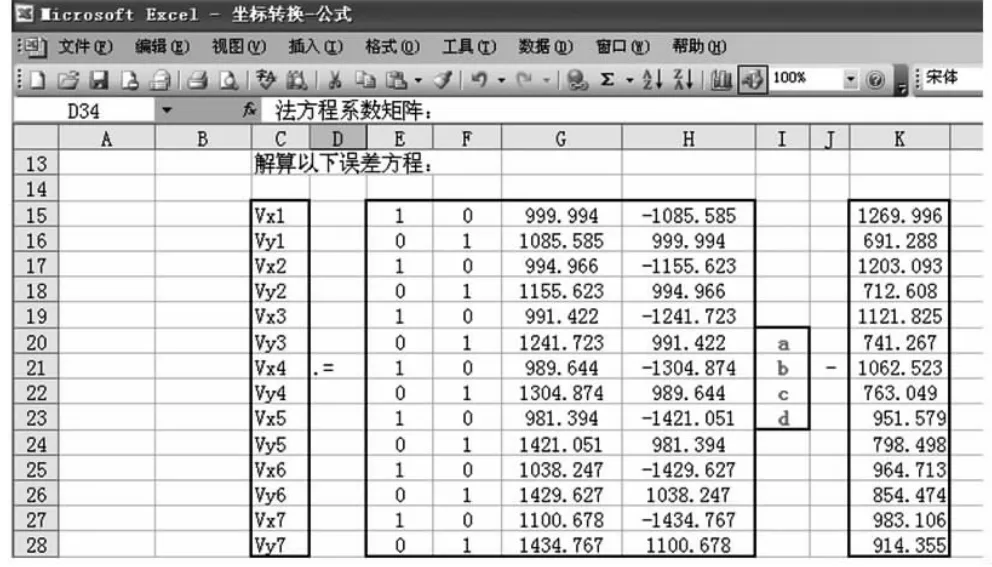
图3 列立误差方程

2.3 解算误差方程

如图4所示，误差方程的解算如下：

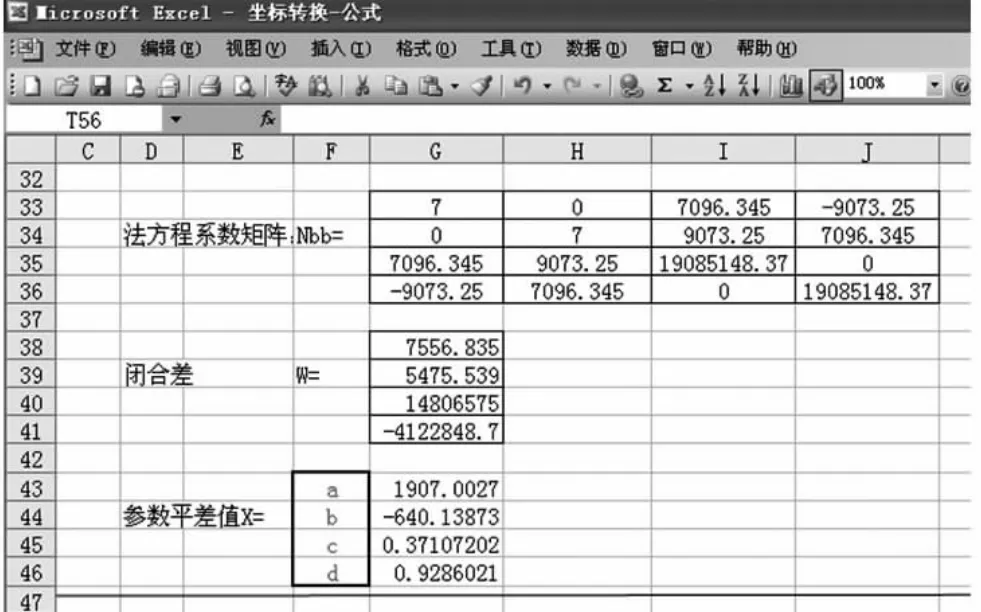
图4 误差方程解算

于是可得平差参数 a＝1907.0027，b＝-640.13873，c＝0.37107202，d＝0.9286021。

2.4 坐标的转换

为了验证所计算的平差参数，如图5所示，将点号为1、2、…、7的点坐标代入，并同时计算了点号为8、9、10的点坐标：

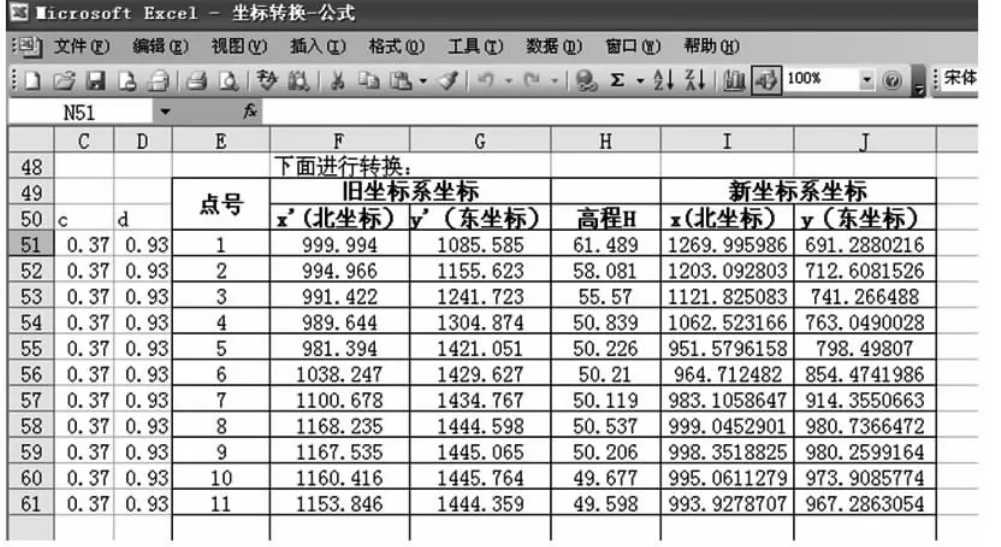
图5 坐标转换

通过进行坐标转换，参照图2与图5的坐标数据，可以比较点号为1、2、…、7的点在转换前后是一样的（忽略小数位的取舍影响）。依此，可以进一步对其他的点进行相应的转换。

3 结论

利用Excel，依据间接平差原理，本文很好地实现了坐标的转换。但在使用时需注意以下几点：

（1）需要注意公共点的个数n必须大于3，理论上越大越好；

（2）由于小数位的取舍影响，使得参与计算的已知点在转换前后的坐标略有微小差异；

（3）本文重复利用了Excel的函数功能，在进行运算时要明白各种函数的意思。

［1］武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].武汉大学出版社,2003.

［2］王永,等.利用Excel绘制误差椭圆的方法[J].矿山测量,2008,12.

［3］泥立丽,等.基于Excel的绘制误差曲线的方法[J].矿山测量,2010,6.

［4］王永,等.基于分形的线要素综合数据处理方法[J].矿山测量,2009,10.