改进的PID神经网络在黑液液位控制中的应用

邓 肖 刘宗玲 杨 朝 胡慕伊

(南京林业大学江苏省制浆造纸科学与技术重点实验室，江苏南京，210037)

在碱回收蒸发工段，系统蒸发罐内黑液液位的变化会导致罐内压力的变化，使蒸发器内受热不均匀，黑液黏度变大，造成蒸发板结垢，黑液得不到充分的蒸发热，蒸发失效。因此，对碱回收蒸发工段控制来说，各效蒸发器、闪蒸罐、黑液槽及自蒸发器液位的精确控制至关重要。在碱回收控制系统中黑液液位受蒸汽温度、压力及自身不断变化(能量传递给液体或从液体吸收能量)特性等因素的影响，具有非线性、大时滞及时变性等特点，难以用完整的数学解析式来描述液位变化的真实情况。因此，要使黑液液位控制取得最佳响应，依靠一般PID控制算法进行控制效果不理想［1］。

PID神经网络(PIDNN)是一种将常规PID控制技术和神经网络融为一体的新型神经网络，PIDNN既具常规PID控制器结构简单的优点，又具有神经网络自学习、自适应之能力，能够在很大程度上克服一般神经网络收敛速度慢、容易陷入局部最小值的问题。通过在Matlab环境中进行仿真实验，结果表明，PIDNN具有一定的自适应性和鲁棒性，与常规PID算法和基于BP神经网络算法相比，根据仿真结果可以推论，PIDNN算法可较好地实现对黑液液位的有效控制。

1 PIDNN控制理论

基于PIDNN的单变量控制［2］系统结构如图1所示。PIDNN作为控制器，其输入值是被控量设定值和被控量实际值，网络的输出作为控制量送入被控对象输入端。

1.1 前向算法

PIDNN的输入层有2个神经元，可分别输入系统的给定值r和测量值y。

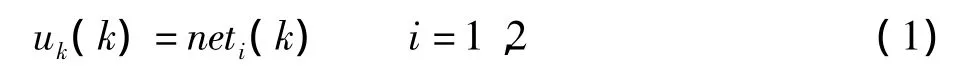
输入层神经元的输入为:输入层神经元的输出与输入相等。

隐含层是神经网络中最重要的层次，PIDNN的隐含层有3个神经元，分别为比例元、积分元和微分元，神经元各自的输入均为:

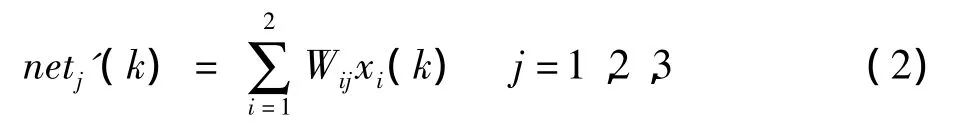
式中，Wij为输入层至隐含层的连接权重值。

比例元的状态为:u1'(k)=net1'(k)

积分元的状态为:u2'(k)=u2'(k-1)+net2'(k)

微分元的状态为:u3'(k)=net3'(k)-net3'(k-1)

隐含层各神经元的输出为:

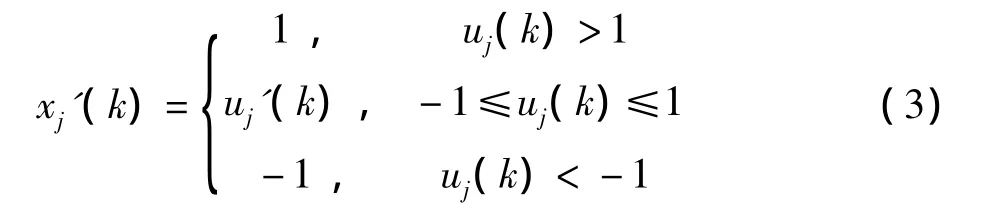
PIDNN的输出层结构简单，只包含1个神经元，完成网络的总和输出功能为:

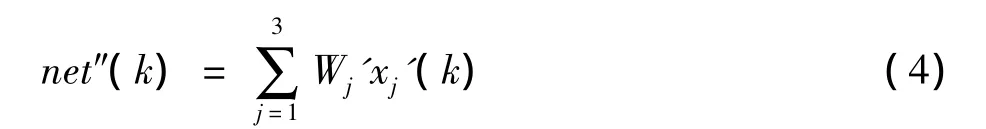
式中，xj'(k)为隐含层各神经元输出值;Wj'为隐含层至输出层的连接权重值。

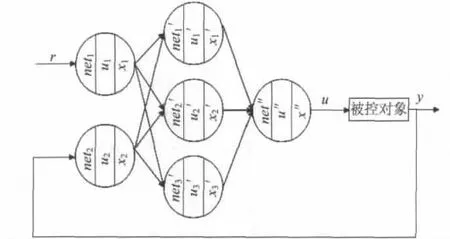
图1 PIDNN单变量控制系统结构图

输出层神经元的状态为:

输出层神经元的输出函数与网络中其他神经元的输出函数相同，输出为:

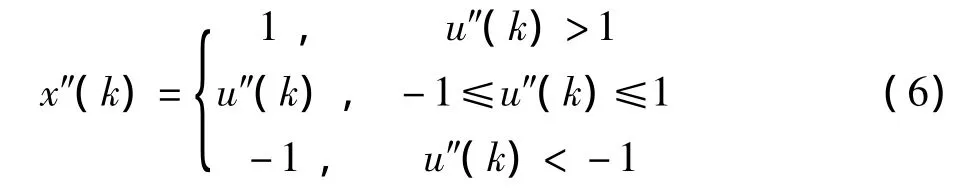
而PIDNN的输出u(k)等于输出层神经元的输出，即:

1.2 反传算法

通过误差反传算法［3］完成网络权重值的修改、学习和记忆的功能。PIDNN训练和学习的目的是使被控变量设定值和被控变量实际值的偏差最小。即整个网络以偏差最小为训练学习的准则和目标。

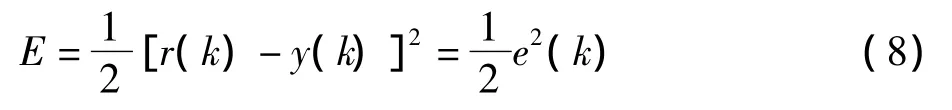
当网络学习k步后，隐含层至输出层的权重迭代公式为:

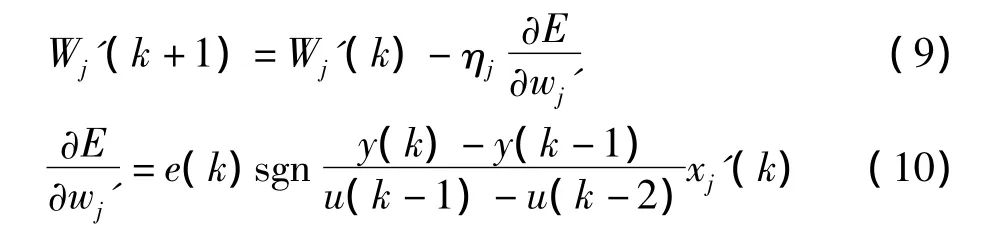
式中，ηj为学习步长。

当网络学习k步后，输入层至隐含层的权值迭代公式为:

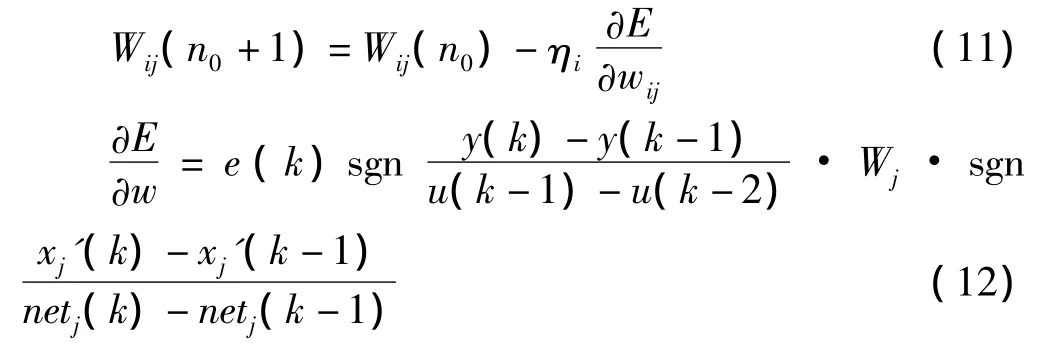
式中，ηi为学习步长。

2 连接权重初值的选取

神经网络连接权重初值决定了网络的起始点和收敛的初始方向，恰当的权重初值可使网络的学习和收敛速度加快，且能避免陷入局部最小值。常规神经网络连接权重初值的选取一般取随机数，但会存在以下问题。

(1)权重初值取随机数，网络学习的起始点和收敛的初始方向都是随机的，需要经过反复训练和学习，收敛速度慢。此外，对于采用反传算法的神经网络，随机的初始权值容易使收敛陷入局部最小值。

(2)神经网络作为控制系统中的控制器，若网络初始权值取随机数，很难保证系统初始的稳定性，无应用价值。

PIDNN是内嵌PID控制规律的神经网络，其权重初值的选取有独特的原则，可以参照PID控制器的特点确定［4］。

2.1 输入层至隐含层的初始权值

根据PID控制算法的特点，为了实现(r，y)→e的映射，选取输入层至隐含层的连接权重初值为:

W1j=1，W2j=-1

2.2 隐含层至输出层的初始权值

选取PIDNN隐含层至输出层的初始权值，使PIDNN的初始输出等价于PID控制器的输出。故隐含层至输出层的初始权值选取为:

W1'=kP，W2'=kI，W3'=kD

按照以上规则选取初始权值时，经PIDNN前向计算得:

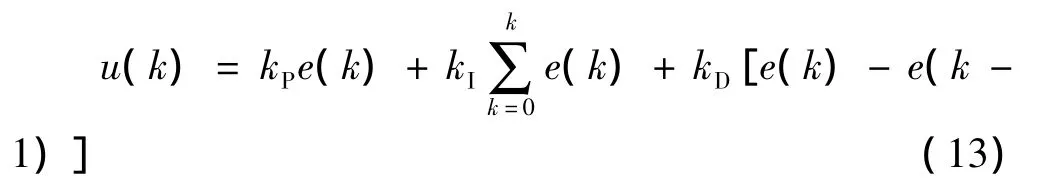
由公式(13)可知，PIDNN选取合适的权重初值时可以与PID控制器等价。因此，可利用PID经验值确定PIDNN的初始权值，使系统初始稳定，不陷入局部极小值。在此基础上，通过在线学习和训练，调整网络连接权重值，从而使PIDNN具备较好的控制效果。

对于没有PID控制规律先验知识的系统，一般选取随机数为连接权初始值，这样网络学习的起始点和收敛起始方向是随机的，若要使收敛方向归于正确，必然需要经过长期反复训练激励和学习。因此，对于无PID先验知识的系统初始值必须加以改进。

3 控制系统的改进

PIDNN具有PID控制和神经网络的双重优点。为完善PIDNN控制系统的性能，扩大其使用范围，可做如下改进［3］。

3.1 改进输出部分的函数

将PIDNN的输出值限制在［-1，1］内，可以加快数据处理速度，使收敛加快。PIDNN输出部分函数一般采用比例阀值函数，使神经网络的输出x″(k)被阀值函数限幅在［-1，1］。若PIDNN输出层的输出连续出现x″=1(或 x″=-1)，则被控对象的输入值u(k)=u(k-1)为1或-1，则sgn(u(k)-u(k-1))=0，从而使得反传算法中的 Wj'(k)≈Wj'(k)，Wij(k)=Wij(k-1)，由此造成网络收敛速度缓慢，甚至可能陷入局部极小值。

改进的方法是用正切函数tanh替换比例阀值函数，双曲线函数tanh(x)是逐渐逼近1和-1的，在一个大的范围内尽可能地使反传算式中的sgn(u(k)-u(k-1))≠0，从而避免神经网络过早陷入局部极小值。

3.2 附加动量项法

由于PIDNN与BP都是以梯度下降为调整权值依据，因此，用于BP的增加动量项也应该可以适用于PIDNN。附加动量项后，网络在修正权值时不仅考虑误差在梯度上的作用，而且考虑误差曲面上变化的趋势。动量项的本质就是每个加权调节量上加一项正比于前次加权变化量的值［5］。其形式为:

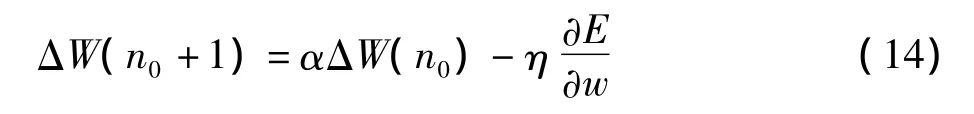
式中，α为动量系数，一般取小于0.9的小数。引入动量项后，促使权值的调节向着误差曲面底部的平均方向变化。当权值进入误差曲面底部的平坦区时，避免出现ΔW=0，从而使网络不陷入局部极小值。

4 仿真结果及分析

为了验证PIDNN控制的优越性，本研究通过对黑液液位控制系统的常规PID算法、基于BP神经网络算法和PIDNN算法的仿真，进行了黑液液位控制效果的比较。在进行仿真的过程中，黑液液位变化过程的数学模型可以近似等效为一阶惯性环节加纯滞后，经过相关推导得到黑液液位传递函数［6］为:

本文中进行的系统仿真设计均在Matlab环境下进行。

(1)在常规 PID 算法中，kp=3.05，ki=2.3，kd=1.01。

(2)在基于BP神经网络算法中，神经网络的结构选择4-5-3，学习步长选择η=0.2。

输入层至隐含层初始权重值选取为:

隐含层至输出层初始权重值选取为:

(3)PIDNN控制系统流程

第一步，将被控对象的传递函数转化为差分方程形式，Matlab控制系统工具箱中提供了c2d()函数［6］，将连续系统变为采样系统。

式中，T为采样时间，取T=1 s;method为采样方法，选取zoh零阶保持器。

第二步，初始化设置，PIDNN的输入层至隐含层的权系数、隐含层至输出层的权系数以及学习步长等参数。其中:

输入层至隐含层初始权值:Wij=rand(3，2)/4;

隐含层至输出层初始权值:Wj'=rand(1，3)/4;

网络的学习步长:η=0.2。

第三步，令k=k+1，k≤200(采样步数)。

第四步，根据给定的输入信号，进行前向算法，计算出控制器的输出u(k)。

第五步，进行反传算法，调整PIDNN的各项参数。

第六步，判断k值，如果k≤200，返回第四步。否则，执行下一步。

第七步，画图。

在Matlab中编程实现PIDNN算法，下面给出算法的部分核心代码:

%前向算法

ui(1，k)=ri(k);%输入层计算

ui(2，k)=Y(k);

for i=1:2

xi(i，k)=ui(i，k);

end

for j=1:3;%隐含层计算

uj(j，k)=0;

for

i=1:2;

uj(j，k)=uj(j，k)+xi(i，k)*wij(i，j，n);

end

end

…………

%反传算法

disp(［‘反传算法开始:迭代次数:’，num2str(n)，‘/’，num2str(MaxNum)］);

if Je(n)＜miniE%如果目标函数值小于预定值，停止

disp(‘反传算法break结束’);

break;

end

if n==1‖(n＞1＆(Je(n)＜=Je(n-1)))%如果本次目标函数小于或等于上次目标值，权值改变为新值

disp(‘权值改变为新值’);

……

用上述3种控制方法，在Matlab中进行仿真，给定值取为单位阶跃函数，该函数下控制系统性能指标见表1;黑液控制系统的曲线如图2所示。

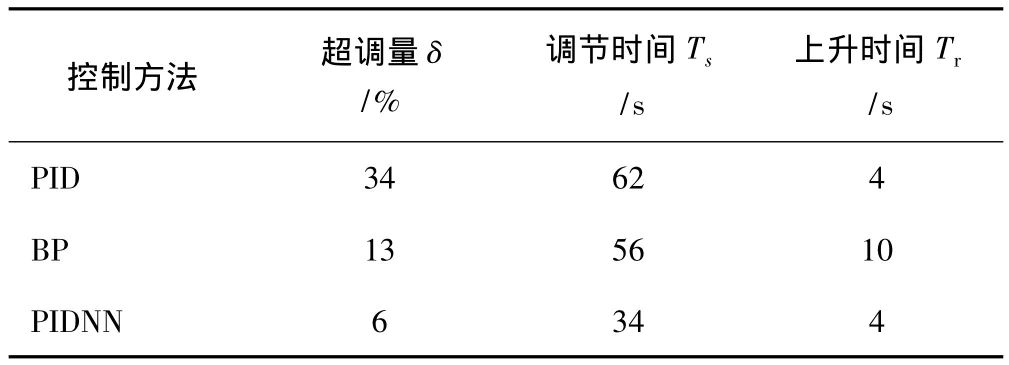
表1 阶跃输入下的控制系统性能指标

由图2和表1可知，与常规 PID算法相比，PIDNN算法系统调节时间减少了28 s，超调量减少(82.4%)更加明显，控制性能的提升十分明显;PIDNN算法与BP神经网络算法相比，调节时间减少了22 s，超调量减少53.8%，性能的优越性比较明显，PIDNN的上升时间也较短，说明PIDNN的响应速度较快，而且PIDNN算法的权重初值相较于BP神经网络算法的权重初值的选取更加简单。

为了进一步验证PIDNN算法的效果，用PIDNN进行时变单变量非线性系统的控制，选取时变单变量系统对象模型为:

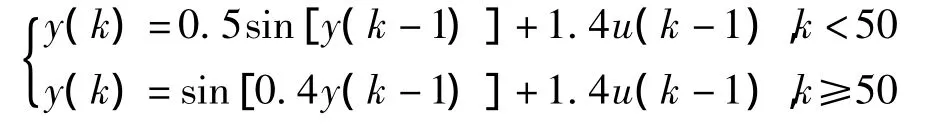
控制系统的输入:r(k)=1(k)，控制器输出计算与权系数调整算法，与上述相同。仿真结果如图3～图6所示。

由图3～图6可知，对象特性发生变化时，由于PID神经网络控制器权系数不断调整，使控制量u(k)变化，当系统的输出经过一段时间调整，仍能跟踪输入。

综上，PIDNN算法有自学习及自适应能力，在不知道对象参数的情况下通过自学习和参数调整，最后成功解决了复杂对象的控制。系统在保证很短输出上升时间的同时，只出现很小的超调量，无静差，有较好的稳定性。

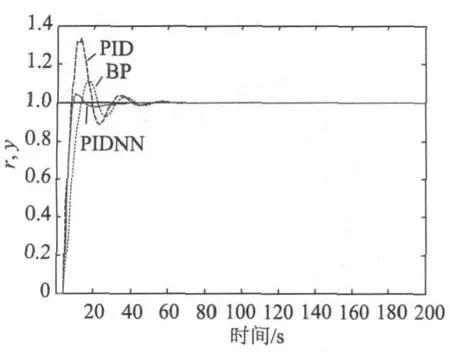
图2 黑液液位阶跃响应曲线

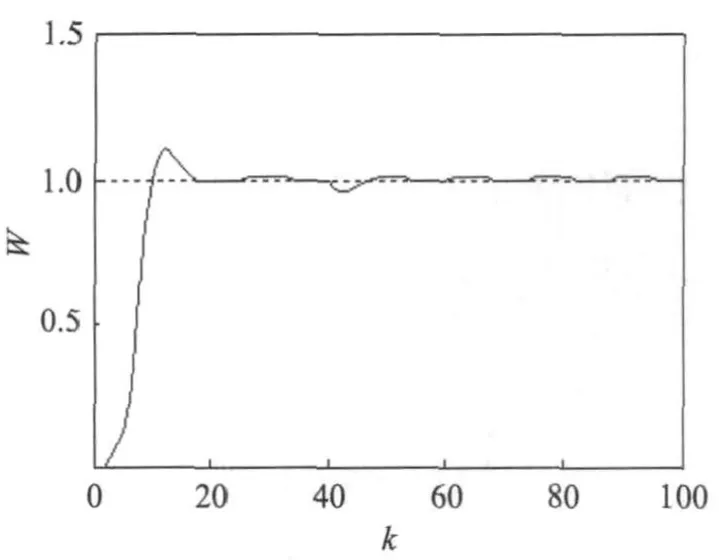
图3 阶跃响应曲线

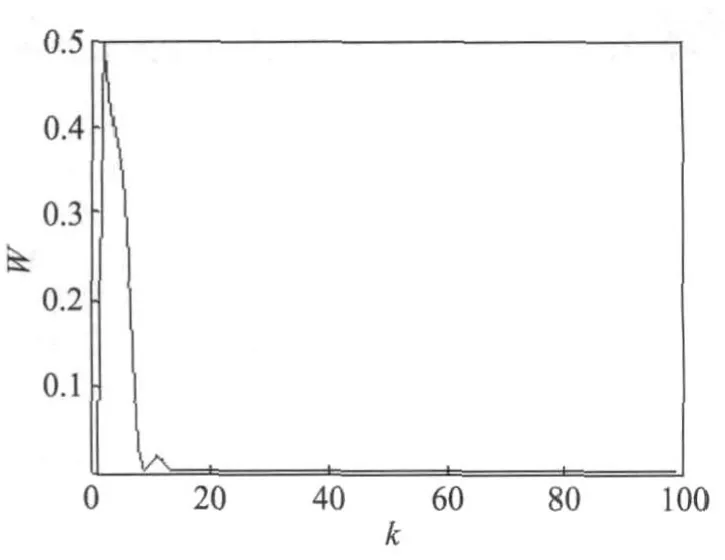
图4 目标函数E的曲线

5 实验

由于MCGS工控机组态软件系统本身的限制，复杂的控制算法由其内置的实时数据库和脚本语言难以实现，故PID神经网络(PIDNN)控制算法采用开发第三方功能构件的方法，使用VB语言编写算法处理程序，生成包含MCGS工控机接口的ActiveDLL策略模块(PIDNN策略模块)，供 MCGS进行策略调用［8］。其实质就是将MCGS的实时数据库作为一个可调用的对象封装起来，VB程序通过MCGS提供的调用接口和操作实时数据库的函数、方法，从实时数据库取得测控数据，运用VB强大的运算能力进行数据分析和算法运算，得到控制量再写回到实时数据库交由MCGS使用。本实验MCGS工控机实际数据库对应于液位控制的实时数据，网络经过在线训练、调整权值，最后对液位实施控制。

用改进的PID神经网络控制系统对黑液液位进行控制时，系统运行效果如图7所示。图7可知，该控制系统控制效果较好。

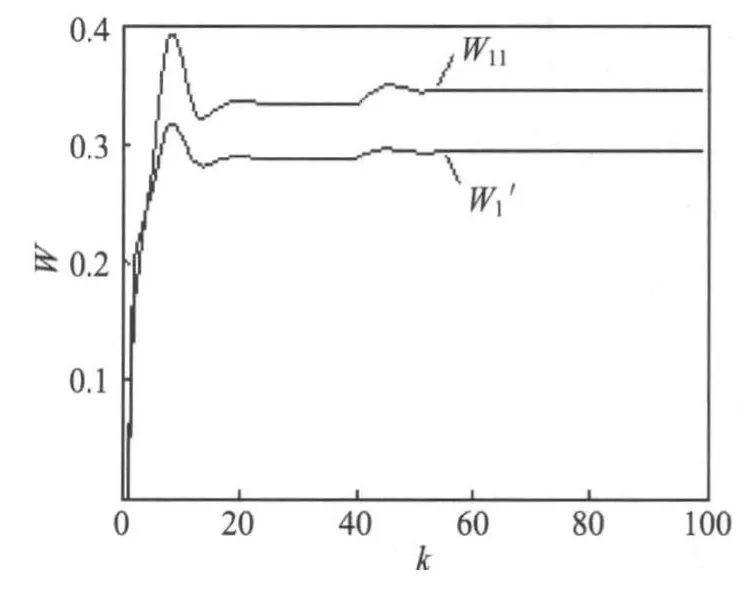
图5 部分权值调整过程曲线

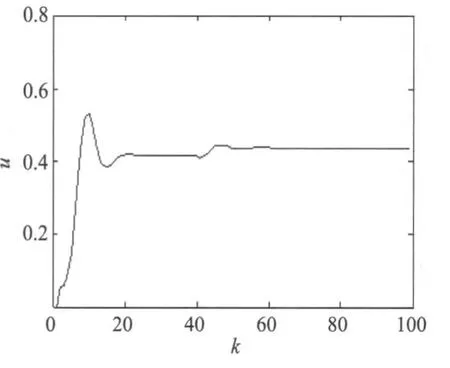
图6 控制量u的曲线

图7 PIDNN在MCGS工控机中对黑液液位的控制曲线

6 结论

对碱回收蒸发工段的黑液液位进行了仿真控制，给出了用BP神经网络和常规PID相结合的PIDNN神经网络控制器，解决了PID对非线性时变系统难以精确控制的问题，避免了BP神经网络权重值难以确定以及可能陷入局部极小值的缺点。根据仿真结果可以推论，PIDNN控制算法可较好地实现黑液液位的有效控制，PIDNN表现出了良好的自适应性和鲁棒性。

［1］曹 露，胡慕伊.神经网路在碱回收蒸发工段中的应用研究［D］.南京:南京林业大学，2012.

［2］舒怀林.PID神经网路及其控制系统［M］.北京:国防工业出版社，2006.

［3］徐丽娜.神经网络控制(［M］.2版.北京:电子工业出版社，2009.

［4］李文峰，刘军营，盛 蕾.PID神经网络控制系统的稳定性分析与改进［J］.山东理工大学学报:自然科学版，2008，22(2):57.

［5］吕 俊，张兴华.几种快速BP算法的比较研究［J］.现代电子技术，2003，167(24):96.

［6］高进更.模糊控制在造纸碱回收系统中的应用研究［D］.兰州:兰州理工大学，2009.

［7］蔡启仲.控制系统计算机辅助设计［M］.北京:科学出版社，2000.

［8］祝佳宁.计算机控制实验装置及PID神经网络控制系统研究［D］.广州:广州大学，2009.