非能动余热排出系统模化及验证分析

武玉增 李常伟

（中国船舶及海洋工程设计研究院 上海 200011）

引 言

反应堆事故停堆后，堆芯剩余功率十分可观。核动力装置一般采用能动和非能动余热排出系统带走这部分热量，一旦发生失电事故（包括正常电源和可靠电源全部丧失），能动余热排出系统失去动力源而失效，而非能动余热排出系统能够不依靠外界动力源导出反应堆堆芯中的衰变热，保障反应堆的安全。不过，非能动余热排出系统在实际工程中设备巨大、价值不菲，故难以进行1∶1的工程实验。本文拟通过模化理论对其换热特性等方面进行分析，验证运用模化理论分析非能动余热排出系统的正确性。

［1］，事故后非能动余热排出系统主要以单相和两相自然循环流动形式带走堆芯余热。对于单相流动情况，模化理论最早由Heisler和 Singer［2］以及 Heisler［3］等人应用于液态金属模化相似准则分析。关于单相自然循环系统和两相自然循环系统的模化研究，Ishii M［4］和 Zuber［5-6］已经展开大量的研究工作，并且已经形成成熟的理论。国内卢冬华［7-8］等人在此基础上也进行了深入的分析和研究。本文主要应用Ishii的模化理论，以某核电厂压水堆为原型，对其主回路（一回路）设置的一套非能动余热排出系统进行模化分析。通过模化分析确定一回路失电事故工况下非能动余热排出系统的模化比例系统。采用RELAP5/MOD3.2软件对工程原型和模化系统进行数值计算，验证非能动余热排出系统模化分析的正确性。因本文只是验证模化分析的准确性，故对船用反应堆的非能动余热排出系统同样具有参考意义。

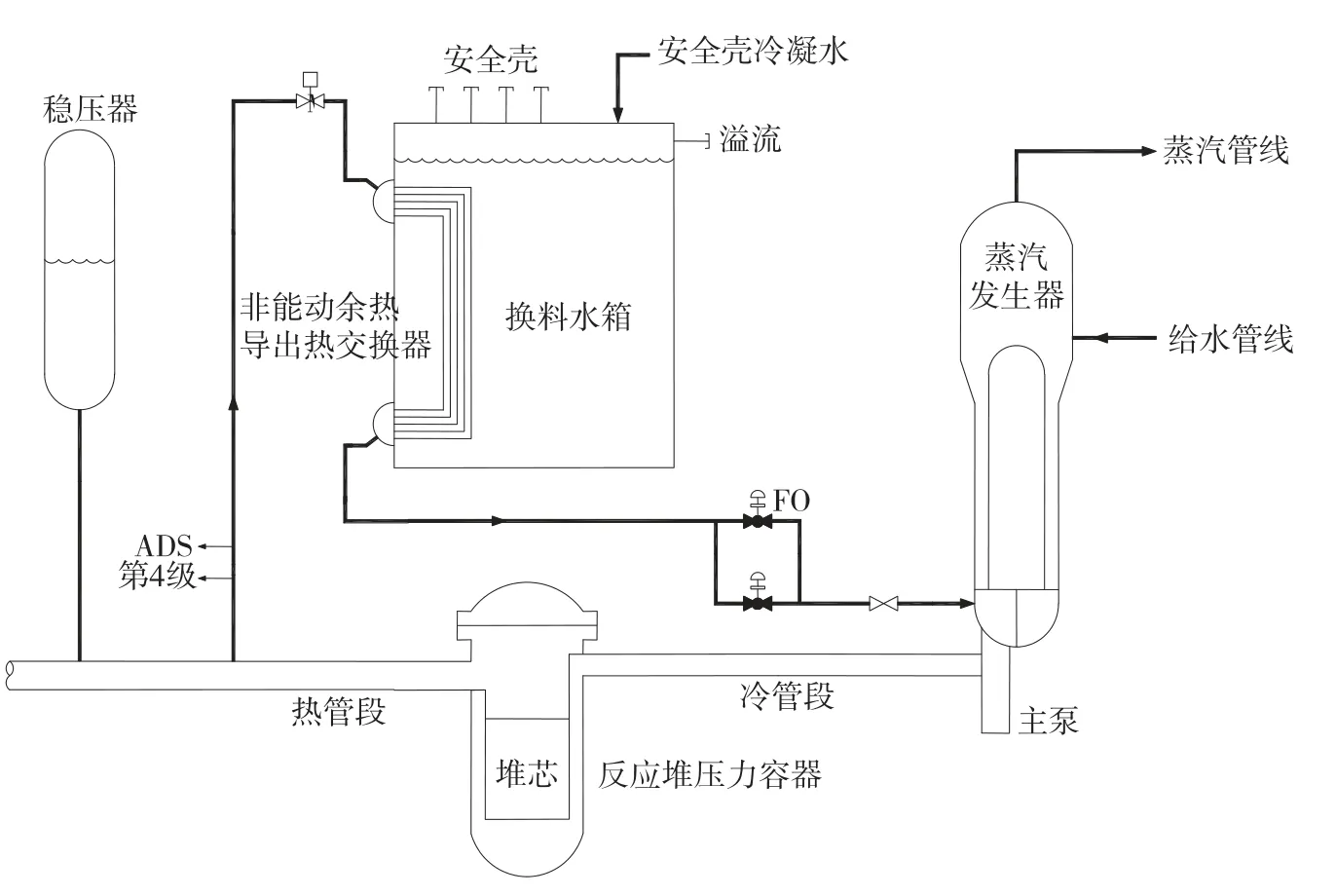
图1 一次侧回路上设置的非能动余热排出系统

1 原型回路系统

某现役反应堆一次侧回路上设置的非能动余热排出系统如图1所示。

假设在反应堆稳态运行过程中发生失电事故，事故序列参考文献［9］，参照该事故序列，运用RELAP5/MOD3.2软件对该事故序列下的非能动余热排出回路进行建模和节点划分（见图2），并对该系统排热性能进行计算分析。

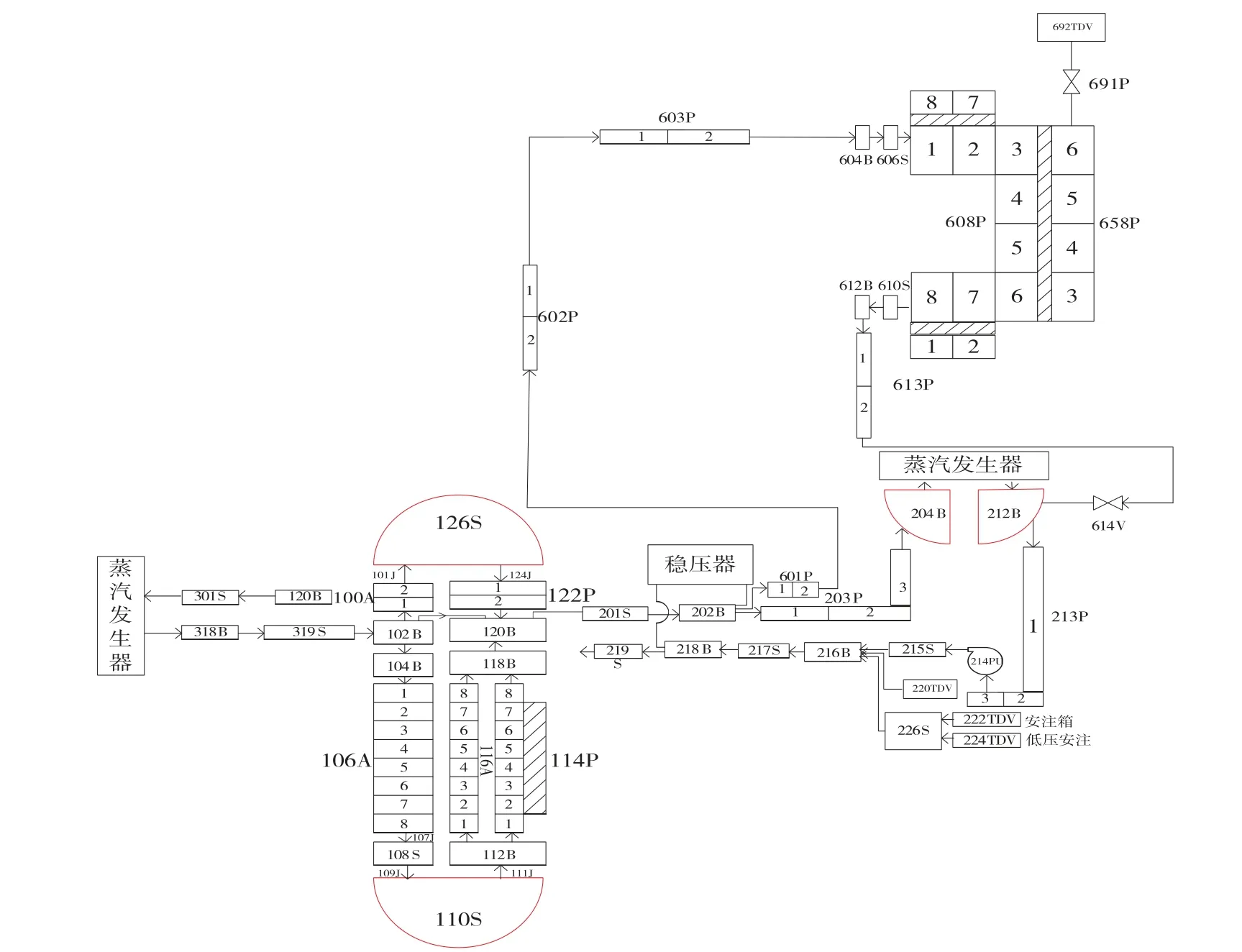
图2 RELAP5/MOD3.2计算节点图

0～500 s为稳态运行阶段。500 s时刻，引入全船断电事故；全船断电事故发生后，由稳压器液位信号和蒸汽发生器窄量程液位信号同时控制非能动余热排出换热器的开启。

图3为主回路循环中最高冷却剂温度与相应压力下饱和温度的变化曲线。通过图3发现，在发生全船断电事故下，非能动余热排出系统能够有效带走堆芯内部的余热，反应堆一次侧循环流体最高温度在整个过程中低于相应压力下饱和温度，因此，在整个非能动余热排出回路内只有单相自然循环流动。

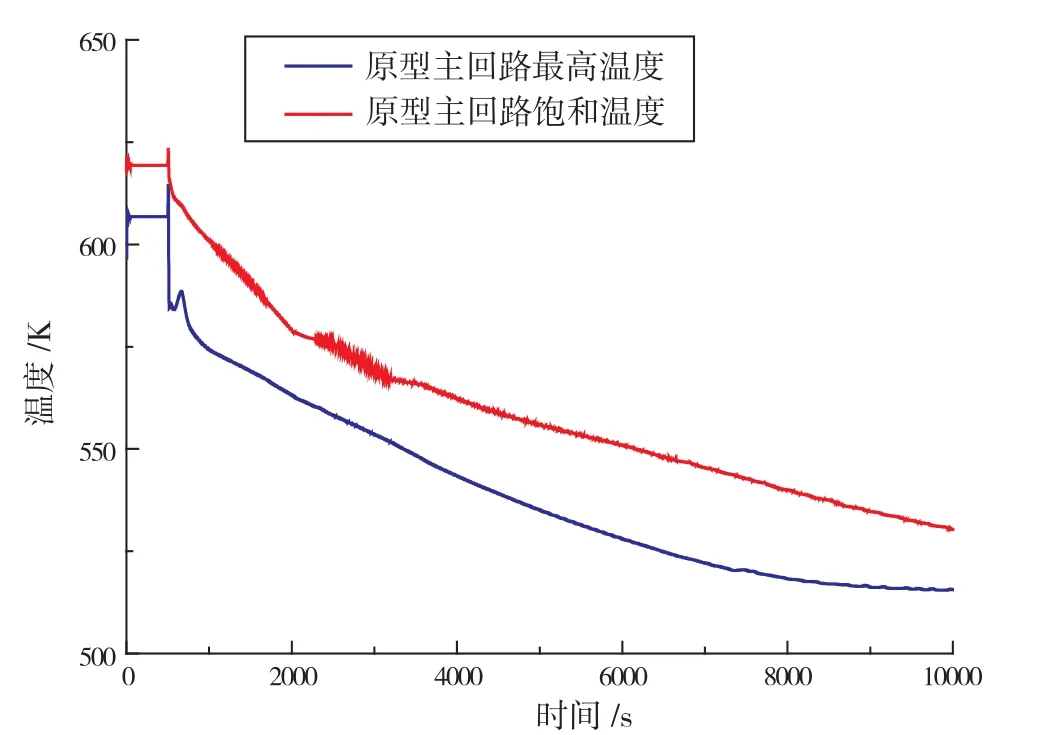
图3 原型主回路最高温度与饱和温度变化

基于上述分析，在对非能动余热排出系统原型进行比例模化时，就可以采用自然循环单相模化理论进行模化分析。

2 模化过程

参考意大利SPES实验系统的原始设计模化比例，假设等压条件下，高度比体积比为了更好地使模型模拟原型的换热特性，需要保证模型和原型的换热部分的当量水力直径相同［10］，即换热构件部分的dR=1。

2.1 模化理论

非能动余热排出系统的自然循环回路整体设备复杂，需进行一定的假设来满足模化分析要求：

（1）原型和模型的流动工质具有相同的特性参数；

（2）要忽略原型和模型的热损失、轴向传热以及传热方程中的高阶项；

（3）轴向为流动方向，径向为传热方向。［7］

对于非能动余热排出系统自然循环情况，可分为加热段、上升段、C型换热器和下降段四部分，如图4所示。

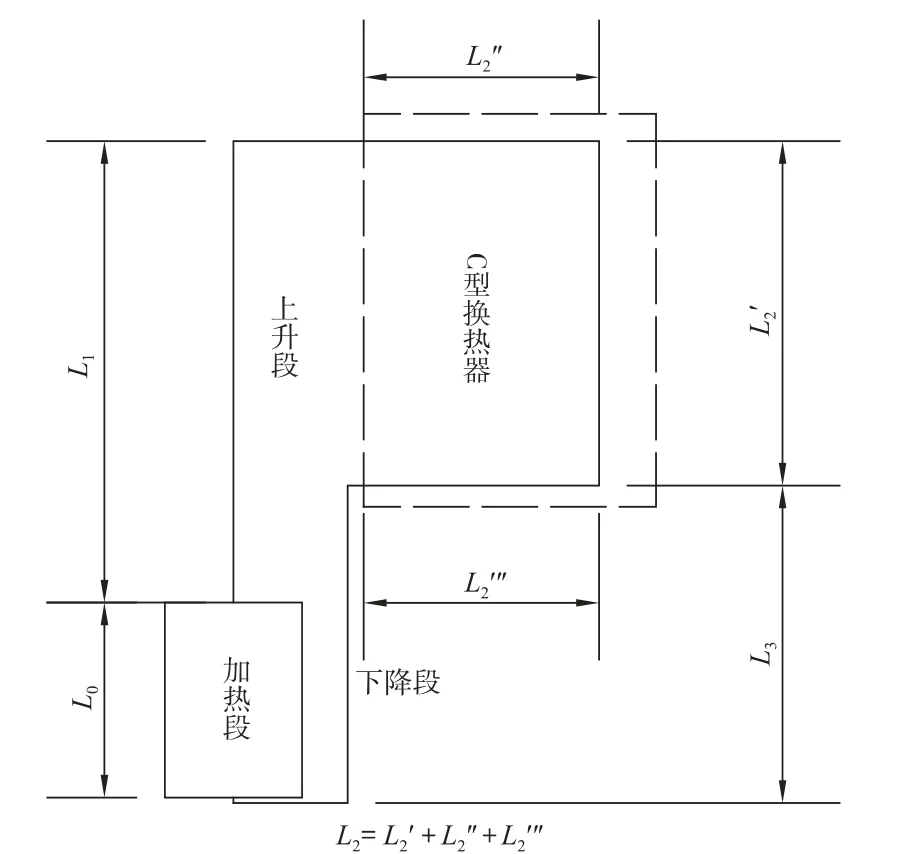
图4 不同换热部分结构示意图

选择特征数，设置方程无量纲参数：

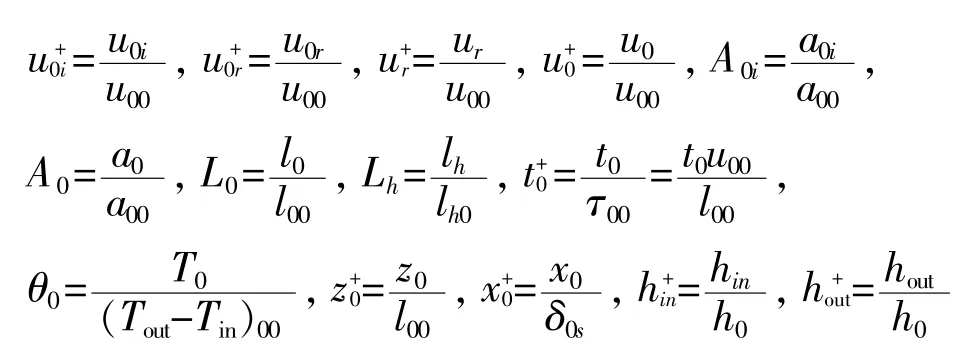
无量纲平衡方程如下：

● 堆芯连续方程

● 动量方程

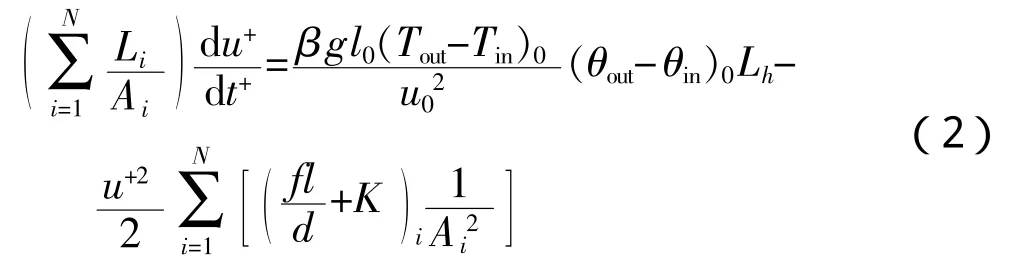
● 堆芯流体能量方程

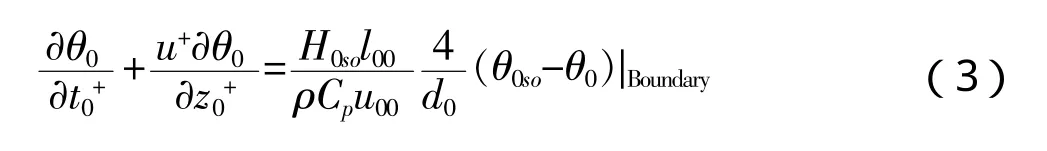
● 堆芯导热方程

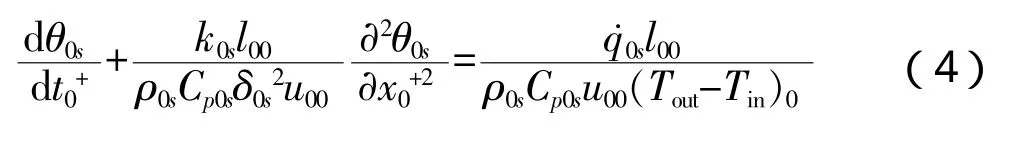
● 堆芯流固界面的边界条件

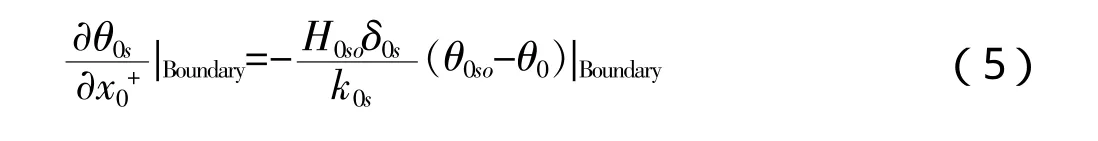
● 堆芯热量传递守恒方程

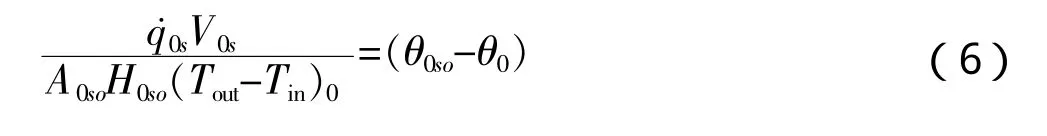
由上述方程可得出如下无量纲相似组：

● 堆芯长度数

● 摩擦数

● 理查德森数

● 堆芯 Stanton 数

● 堆芯热源数

● 堆芯热流密度比

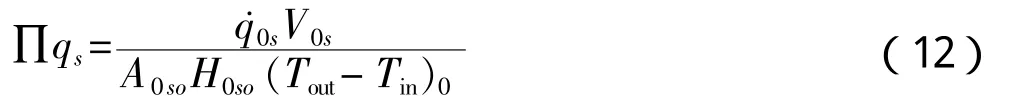
● 堆芯面积数

● 阻力系数比

● 长度系数

● 堆芯时间比数

● 堆芯毕渥数

2.2 主要参数模化比的确定

通过对原型模化理论分析和无量纲方程的描述，得出相应模型的几何特征数、流动特性和传热特性的特征数。通过保持特征数相同来保证模型和原型具有相同特性，即；使长度数及面积数相等来保证具有相同的几何特征。流动特性方面，对于自然循环系统，要求理查德森数和摩擦数相同（即保证模型和原型的驱动压头和流动阻力特性相同），以及Stanton数、热源数、毕渥数、热流密度比相同，以保证换热特性相同。原型和模型的参数比汇总见表1。

表1 模型与原型设计参数比汇总表

本文中所出现的所有物理量的名称及符号见表2，角标名称及符号见表3。

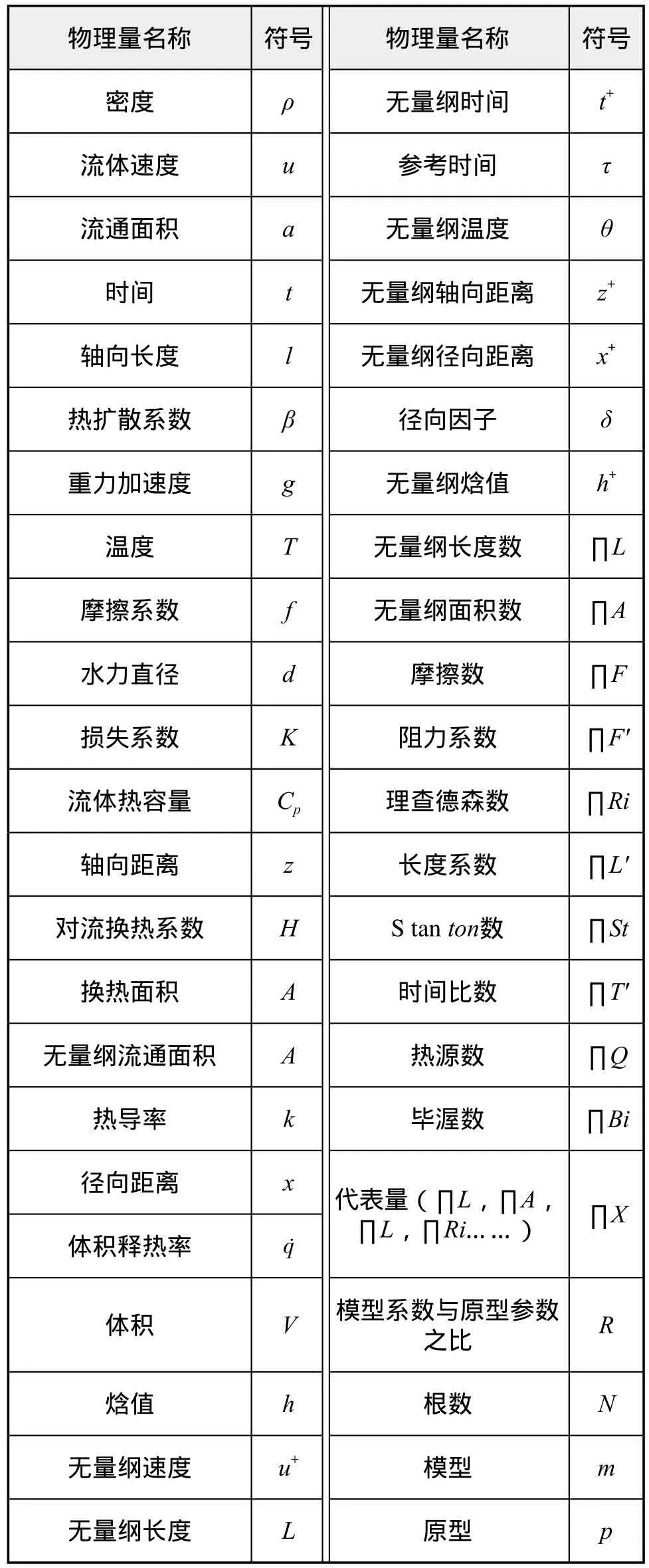
表2 物理量的名称和符号

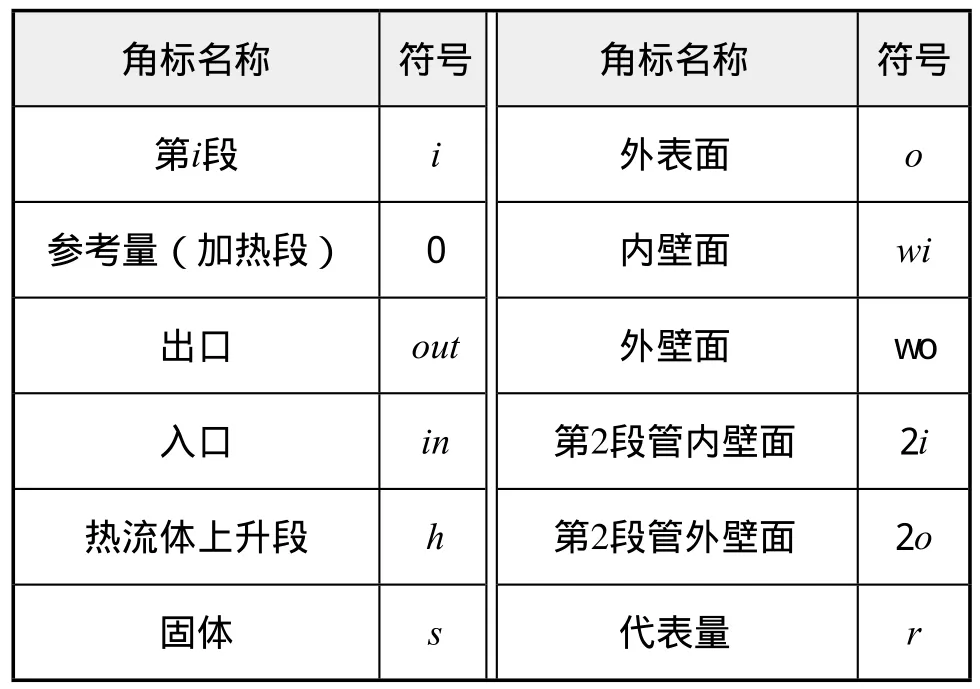
表3 角标名称和符号

3 RELAP5/MOD3.2建模分析

通过以上对堆芯非能动余热排出系统原型模化分析，得出模型的几何参数、流动参数和换热参数的模化参考量。将得出的模型的模化参考量用RELAP5/MOD3.2软件进行计算，并且与原型设计参数下用RELAP5/MOD3.2软件计算出的结果进行对比，验证模化分析的正确性。

3.1 原型和模型计算结果对比分析

提取非能动余热排出系统的原型设计参数和模型模化参考量的RELAP5/MOD3.2软件计算结果，包括计算流量、计算换热功率、计算一回路温度、计算堆芯热功率的瞬态变化量，如图5-图9所示。

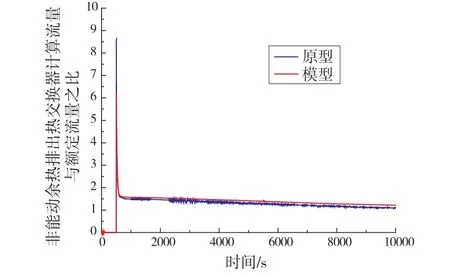
图5 一回路流量变化曲线

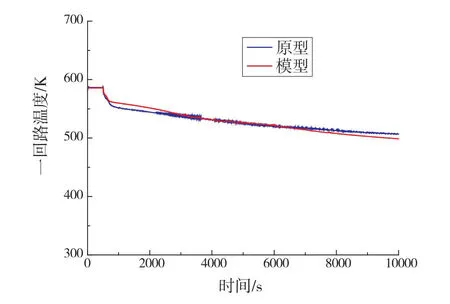
图6 一回路温度变化曲线

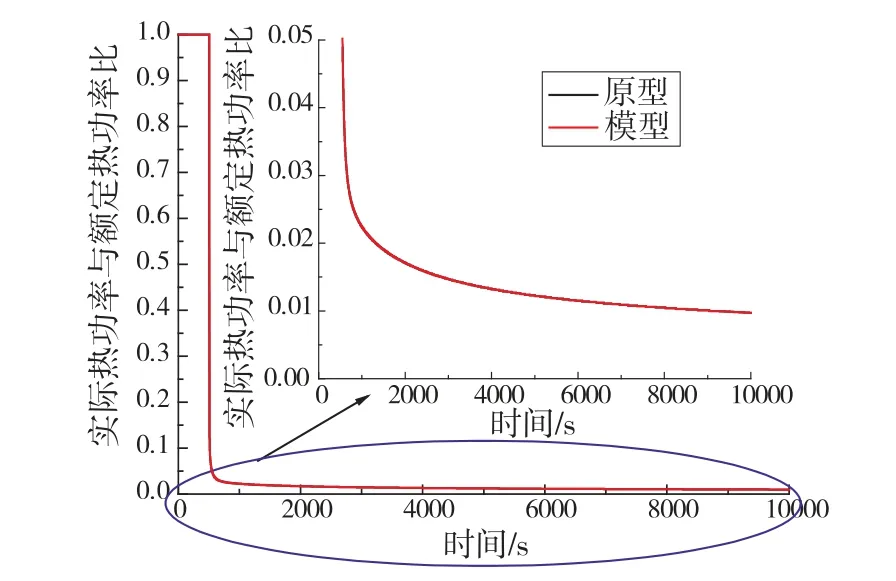
图7 实际热功率与额定热功率之比的变化曲线

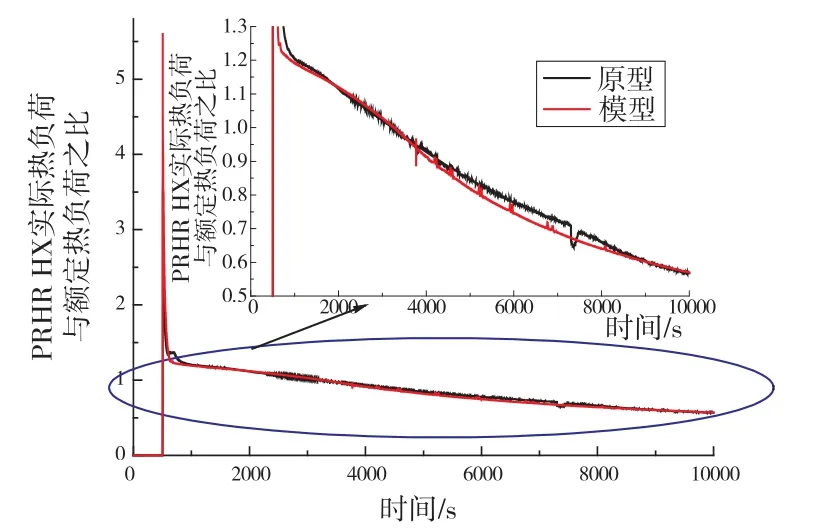
图8 非能动余热排出热交换器实际热负荷与额定热负荷之比

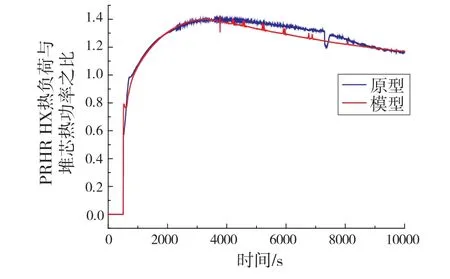
图9 非能动余热排出热交换器热负荷与堆芯热功率之比

如图5所示，在稳态运行过程中，非能动余热排出系统处于未启动状态，因此在0～500 s内非能动余热排出系统并没有流量，在500 s时刻引入事故后，由于启动瞬间冷热端差很大，产生很大的驱动压头，因此，在500 s时刻引入事故瞬间流量急剧增加。在非能动余热排除系统进入稳定运行后，非能动余热排出系统的原型和模型RELAP5/MOD3.2软件流量计算结果与额定流量相近，说明模型能够准确反映原型性能。

从图6看出，在稳态运行工况0～500 s内，原型和模型的一回路温度相同。在500 s时刻引入假想事故工况，非能动余热排出热交换器启动，一回路温度在500～800 s时间段迅速下降到550 K。800～10 000 s时间段，堆芯余热全部由非能动余热排出热交换器带出。在整个模拟过程中，原型和模型的一回路温度随时间变化趋势一致。由于原型水装量大于模型水装量，以至原型热容量大于模型热容量，因此，事故情况下原型的一回路温度下降速率慢。

图7是通过RELAP5/MOD3.2程序计算出的堆芯热功率变化与参考量的比值，图8是通过RELAP5/MOD3.2程序计算出的非能动余热排出热交换器热负荷变化与参考量的比值。在0～500 s时间段内，原型和模型都处在稳态运行阶段，通过RELAP5/MOD3.2程序计算出的堆芯热功率与参考量相同，非能动余热排出热交换器没有启动。在500 s时刻发生假象事故，堆芯热功率迅速下降，非能动余热排出热交换器由蒸汽发生器液位信号触发启动。在非能动余热排出热交换器启动瞬间，堆芯余热热量很高，热惯性大，因此，非能动余热排出热交换器热负荷瞬间大幅度增大。随着堆芯热功率降低，换料水箱温度升高，系统自然循环驱动压头降低，循环流量降低，导致非能动余热排出热交换器的热负荷也随之下降。从图7和图8可知，原型和模型的堆芯热功率变化曲线和非能动余热排出热交换器热负荷变化曲线符合，模型能够模拟原型的堆芯热功率变化。

图9给出RELAP5/MOD3.2程序计算出非能动余热排出热交换器换热功率与堆芯热功率的比值。0～500 s时间内，RELAP5/MOD3.2程序稳态运行，非能动余热排出热交换器没有启动，原型和模型的非能动余热排出热交换器换热功率与堆芯热功率的比值为0。非能动余热排出热交换器启动后，非能动余热排出热交换器热负荷高于堆芯余热功率，能够将堆芯余热全部导出，使得一回路温度随时间逐渐降低，如图6所示。在整个过程中，由于非能动余热排出热交换器和换料水箱之间换热温差逐渐减小，自然循环驱动压头下降，流量下降，如图5所示，导致非能动余热排出系统热负荷降低，因此，4 000 s后曲线呈现下降趋势。从图9可以看出，原型和模型非能动余热排出热交换器热负荷与堆芯热功率比值变化曲线符合。

通过图5-图9所示，在全船断电事故工况下，运用模化理论得出非能动余热排出换热系统模型与原型换热特性能够良好匹配。

4 结 论

通过模化分析确定某核反应堆一回路失电事故工况下非能动余热排出系统的模化比例系统。采用RELAP5/MOD3.2软件对工程原型和模化系统进行了数值计算，数值结果表明非能动余热排出系统的模型能够有效反映工程原型的换热能力，验证了非能动余热排出系统模化分析的正确性。

通过本研究表明，完全可以用模化理论对核动力装置的非能动余热排出系统进行模化，进而进行模型实验，验证非能动余热排出系统的有效性，进一步提高核动力装置的安全性。

［参考文献］

［1］ REYES J N，HOCHREITER L.Scaling analysis for the OSU AP600 test facility（APEX）［J］.Nuclear Engineering and Design，1998，186（1-2）：53-109.

［2］ HEISLER M P，SINGER R M.Facility Requirements for Natural Convection Shutdown Heat Removal System Testing［J］.Hemisphere，Washington，1981 ：113.

［3］ HEISLER M P.Development of scaling requirements for natural convection liquid-metal fast breeder reactor shutdown heat removal test facility［J］.Nuclear Engineering and Design，1982，80：347.

［4］ ISHII M，KATAOKA I.Scaling laws for thermal-hydraulic system under single phase and two-phase natural circulation ［J］.Nuclear Engineering and Design，1984，81（3）：411-425.

［5］ ZUBER Novak，WILSON G E，Mamoru Ishii，An integrated structure and scaling methodology for severe accident technical issue resolution： Development of methodology［J］.Nuclear Engineering and Design，1998，186（1-2）：1-21.

［6］ ZUBER Novak.The effects of complexity，of simplicity and of scaling in thermal-hydraulics［J］.Nuclear Engineering and Design，2001，204（1-3）：1-27.

［7］ 卢冬华，肖泽军，陈炳德.压水堆自然循环比例模化基本方程及相似准则数的研究［J］.核动力工程，2009，30（3）：74-94.

［8］ 卢冬华，肖泽军，陈炳德.运动状态下压水堆自然循环比例模拟方法研究［J］.核动力工程，2009（6）：28-37.

［9］ AP1000核电厂系统与设备［M］.2005.

［10］ JIN Ho Song，KYOO Hwan Bae.Evaluation of analytically scaled models of a pressurized water reactor using the RELAP5/MOD3 computer code ［J］.Nuclear Engineering and Design，2000，199（3）：215-225.