海底地形及弹性对绷紧式系泊系统静力特性影响研究

洪文渊 张火明 王 强 管卫兵 陈阳波

（1.中国计量学院计量测试工程学院 杭州310018；2.卫星海洋环境动力学国家重点实验室 国家海洋局第二海洋研究所 杭州310012）

引 言

陆地和浅海地区的油气过度开发，导致油气资源现已十分匮乏，这是全世界都需要面对的一个棘手问题。深海石油和天然气的开发势在必行，深海平台技术现已成为众多海洋国家的科学家们的研究课题。如何在深海油气开发中抢占先机？对我国未来的发展有着十分重要的战略意义。我国的海域油气资源十分丰富，但其独特的海洋环境和复杂的油气储藏地形却使深海油气开发的钻探、建造需克服诸多技术难关［1］。绷紧式系泊系统近些年来在深海领域得到了成功应用，同时表现出很多独有优势，现已倍受关注［2-3］。

通常在对系泊系统进行研究时会忽略海底地形的影响，将海底看作是水平的刚性基础，假设各系缆锚系点处于同一海底平面上且海底无弹性，而实际工程应用中海底状况往往不是理想的，它对于系泊系统的影响是不能忽略的。唐友刚等人［4-5］计算了平坦海底和不平坦海底的系缆形状、静态张力和浮体平衡位置，发现当海底地形变化较大时，系缆的形状、张力和系泊浮体的运动都会受到一定的影响，尤其是系缆张力。W.Raman-Nair和R.E.Baddour［6］考虑到不平坦海底对系缆的支持力，采用集中质量法提出了海流作用下系缆形状和张力的计算方法。

本文以工作水深为1 500 m的Spar平台为例，对其绷紧式系泊系统进行了静力特性分析［7-8］，通过C++开发了能计算单根纤维缆的张力、系泊系统总水平和总垂直的恢复力-位移特性的程序，在考虑了不同海底锚系点高度对单根系缆张力-位移特性的影响基础上建立海底等效弹簧模型，研究不同海底弹性下的系缆张力、系泊系统总水平和总垂直的恢复力-位移特性。

1 系泊系统静力特性分析

绷紧式系泊系统的系泊缆多选用聚酯纤维材料，而聚酯纤维系泊缆的密度和海水接近，因此不用考虑其重力影响。其流体作用力远小于系缆轴向张力，故本文也忽略不计。

将系缆看成是弹性伸长的弹簧，已知单根纤维系缆静刚度k0、最小破断强度MBL、初始预张力F0、初始长度L0和系统垂直跨距h，便可得到系缆张力与顶端位移的关系。假设系缆上存在水平移动距离为 的端点，另系统平衡位置为0点，依次取2 m、4 m、6 m、…20 m的端点，系缆上端点的总移动范围为0～20 m。

1.1 每一个移点处单根系缆张力的计算方法

1.2 系泊系统在每一位移点处总水平恢复力和总垂直恢复力计算步骤

（1）计算单根系缆在每一位移点处的张力T。

（2）计算出单根系缆在该位移点处的上端点倾角 ，从而得到每根系缆的水平张力Tx和垂直张力Tz为

（3）将得到的每根系缆水平张力Tx向x轴正方向投影后合成即可求得系泊系统在该位移点在x轴方向上的水平恢复力，将每根系缆垂直张力合成即可得系泊系统z方向上的垂直恢复力。

在此，需要着重说明的是步骤（2）和步骤（3）中系泊系统某位移点处沿x轴方向总水平恢复力的求解方法［9］，如图1所示。

图1 总系泊系统静力特性计算示意图

设单根系缆初始水平投影长度为L0，初始布锚角为系缆上端点沿x正向水平移动系缆在海底平面的水平投影长度变为L0+，由三角形余弦定理可得：

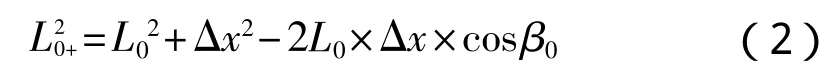
由L0+可求出系缆张力，再由（1）式可得系缆水平张力Tx和垂直张力Tz，然后把水平张力向x轴方向投影即得系缆对系泊系统总水平恢复力的贡献，见式（3）。

其中

将所有系泊缆对整个系泊系统总水平恢复力的贡献叠加求得整个系统在位移为时的水平恢复力。必须注意的是，编程求解某位移点系泊系统恢复力时，需要先判断单根系缆在该位移点是否松弛，若某根系缆完全松弛，必须令其张力为0，否则程序的计算结果会出现负值，即错误的系统恢复力的结果。

2 计算实例

为检验计算程序是否可靠，这里对比文献［10］所使用的系泊分析软件Ariane得到的计算结果，选取4条聚酯系缆的转塔式系泊系统，系泊方式见图2，系缆相关参数见表1。平台主体沿x轴正向移动范围为0～20 m，在忽略系缆自身重力的基础上求解单根系缆的张力。计算结果如图3和图4所示。

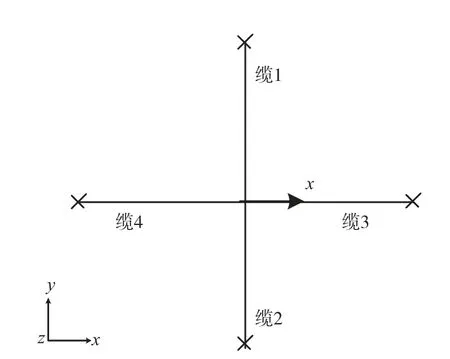
图2 系泊系统平面布置图

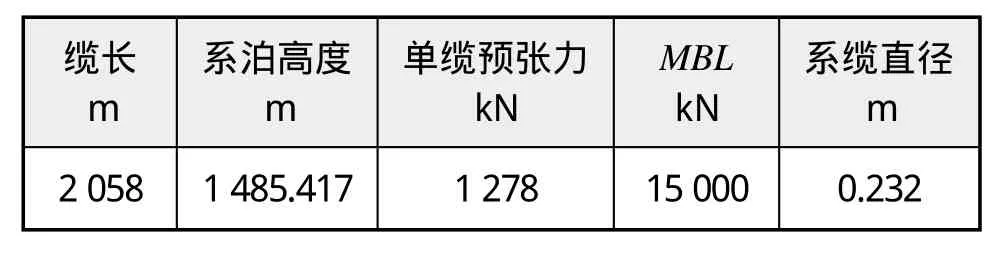
表1 系缆相关参数

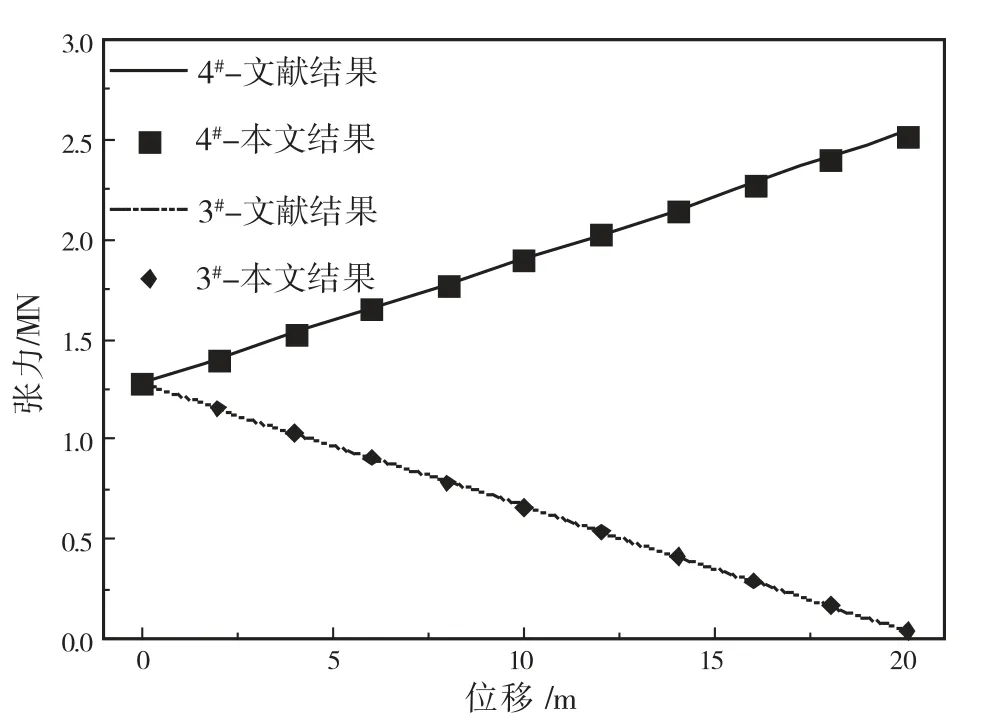
图3 缆3和缆4张力特性曲线

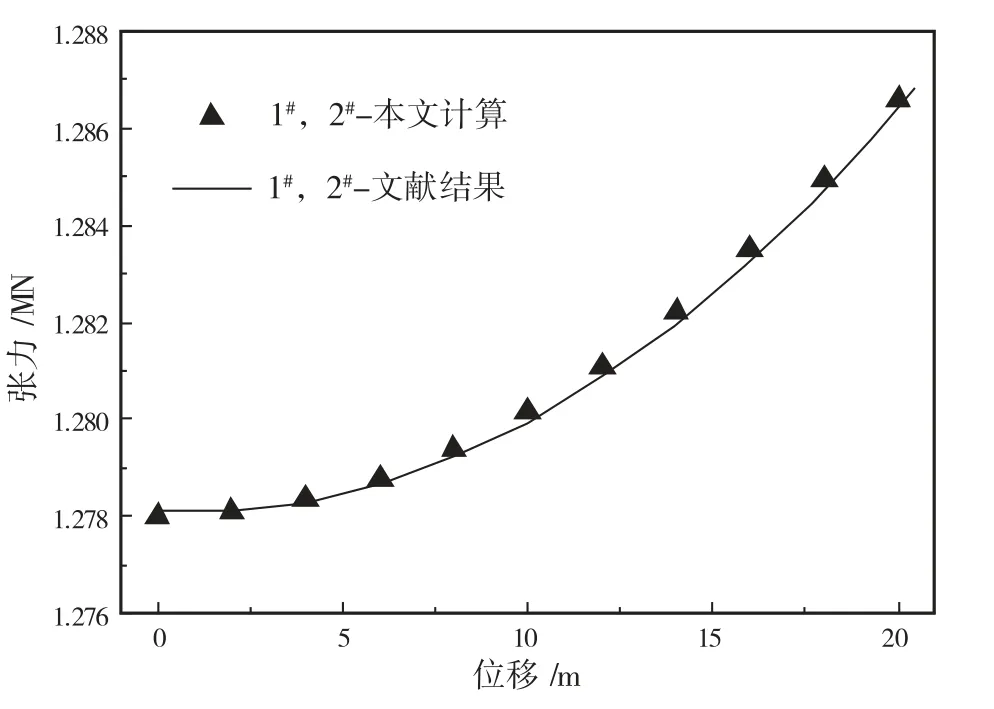
图4 缆1和缆2张力特性曲线

通过将本文结果与文献［10］的计算结果对比可知，本文的计算方法是值得信赖的。系统总水平和垂直恢复力-位移特性曲线将在后面研究海底弹性基础对系统静力特性影响时进行计算。

3 不同海底地形下的单根系缆张力

以第2节中4点系泊系统为例（参见图2），分析海底锚系点高度对于单根聚酯纤维缆张力-位移特性的影响，系缆相关参数请参照上节。在此，我们假设缆4的海底锚系点比其他系缆锚系点低缆4上端点沿x轴正方向发生位移，其运动如图5所示，通过计算还可以得到每一位移点处系缆张力。

图5 缆4运动示意图

在图5中：O为预张力下的系缆上端点，假设A点为缆4的原锚系点，h为原系泊高度，也是另外3缆的系泊高度，现缆4锚系点为A′，可以看出A′点处系缆的系泊高度变为由于各系缆在预张力作用下均处于绷紧状态，即A′和A点处系缆与水平方向的夹角α相同，其值为：

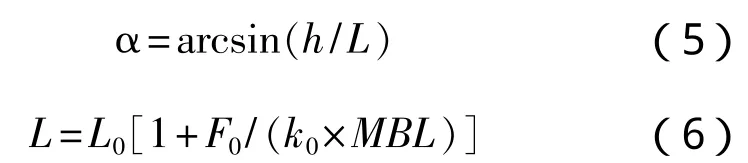
式中：L为锚系点为A点时系缆在预张力下的长度；L0为锚系点在A点时系缆原长；F0为预张力；k0为系缆静刚度；MBL为最小破断强度。故在锚系点A′处系缆在预张力下的长度为：

水平跨距为：

由式（7）及式（8）可以计算出锚系点为A′点时，缆4的原长 ：

计算出以上参数后，由第1节中的单根系缆上端点在每一位移点处的张力理论计算方法可计算出锚系点A′中缆4张力-位移变化关系图，如图6所示。

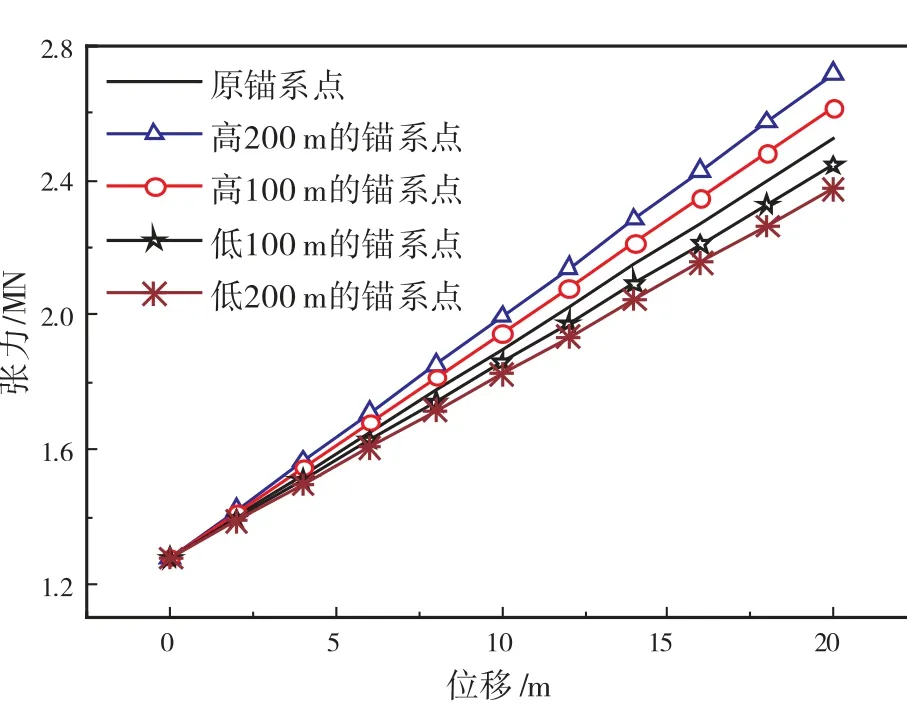
图6 单根系缆系泊点高度对系缆张力的影响

（1）当单根系缆上端点发生相同的位移时，系缆锚系点越低，即系泊高度越大，其轴向张力越小，反之，其轴向张力越大。

（2）相同位移下，单根系缆轴向张力随系泊高度的增加而减小，但幅度较小。

因此，在运用新型绷紧式系泊系统对平台进行定位时，可以通过减少系缆的系泊高度以提高系泊能力。

4 海底弹性对系泊系统及单根系缆力学特性的影响

文献［11］中将海底假设为一个弹性基础，分析海底地形对悬链线系泊缆支持力的影响，通过集中质量法计算风浪流作用下系缆张力。由于本文研究的新型绷紧式系泊系统，忽略系缆自身重力，同时系缆无躺底段，因此海底对系缆无支持力作用。本文对海底建立了简单的物理模型，只将海底看作是线性刚度为ke的等效弹簧，并以此为基础，研究不同海底地形对单根纤维系缆张力-位移特性及总系泊系统水平和垂直恢复力-位移特性的影响。

在此，仍以第2节中4点系泊系统为例，计算平台主体沿x轴正向运动时各系缆张力-位移特性及系泊系统总水平和垂直恢复力-位移特性。

由于海底刚度较大，可能远大于系缆的静刚度，为了显示出海底弹性对系缆张力影响，我们假设其线性刚度为10倍的系缆静刚度，即ke= 10k0，海底等效弹簧初始长度及质量忽略不计。

如图7所示，当系缆上端点沿x轴正向运动时，可以将系缆和海底等效弹簧看作是相互串联的两根系缆，串联后其静刚度变为：

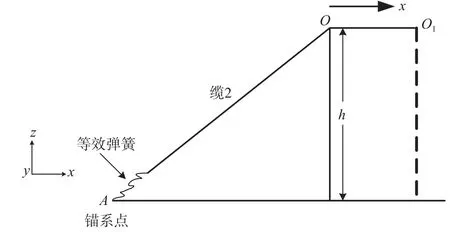
图7 缆2运动示意图

由单根系缆上端点在每一位移点处的张力理论计算方法可计算出各系缆张力-位移变化特性曲线及4点系泊系统总水平和垂直恢复力-位移特性曲线。

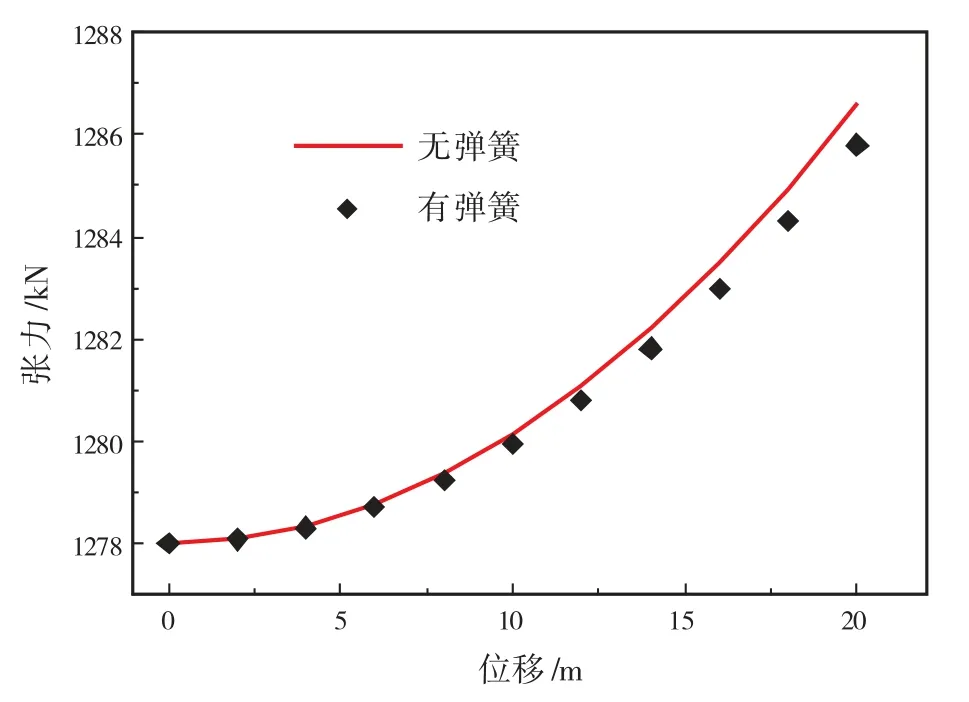
图8 缆1和缆2张力-位移特性曲线

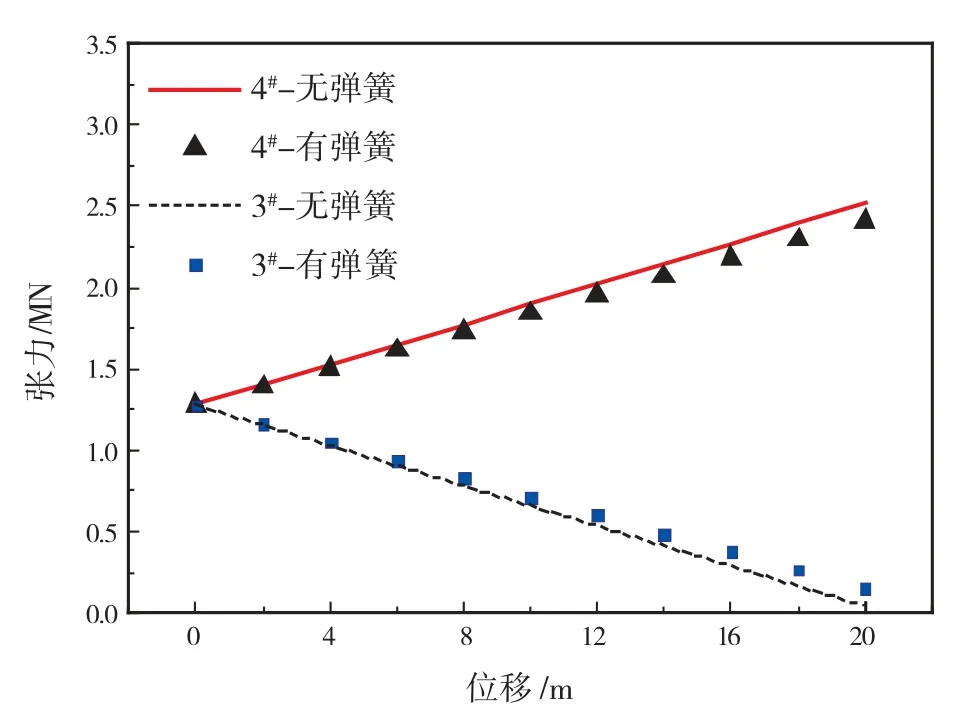
图9 缆3和缆4张力-位移特性曲线

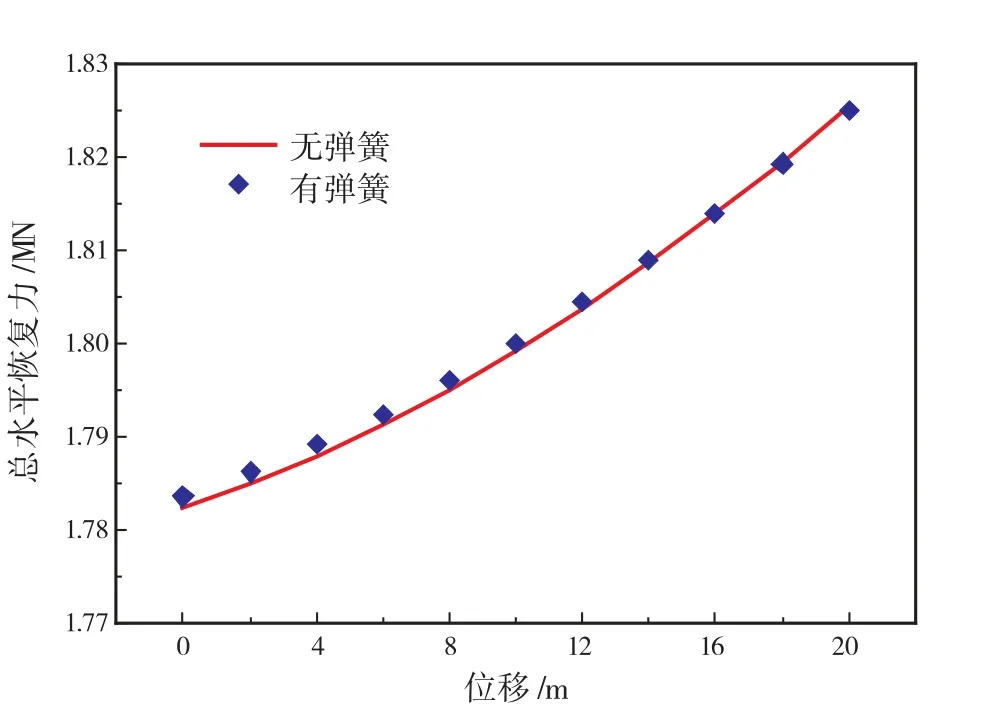
图10 系泊系统总水平恢复力-位移特性曲线

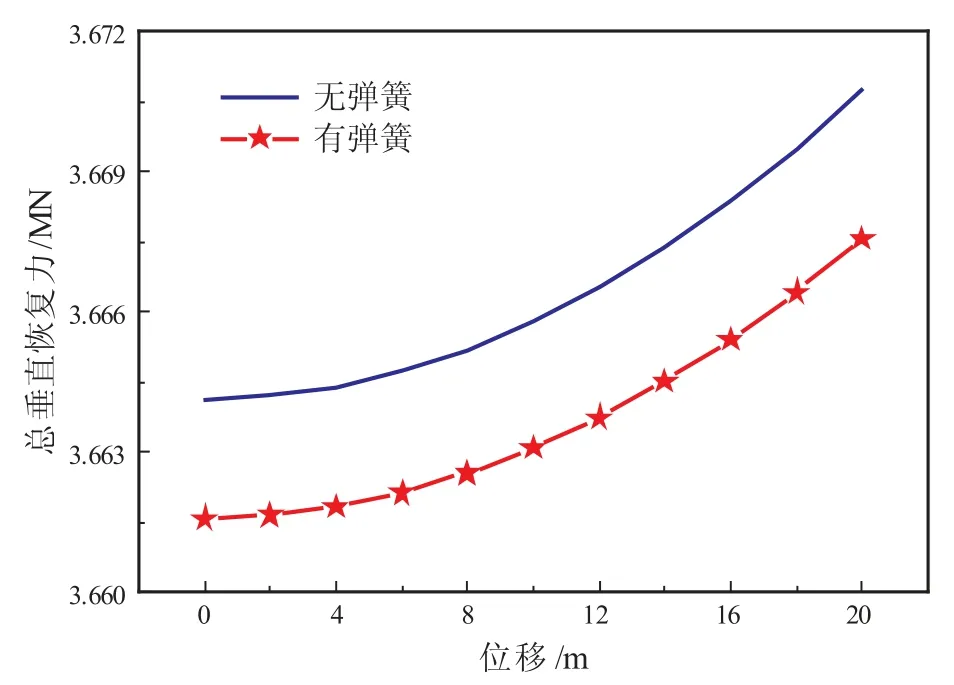
图11 系泊系统总垂直恢复力-位移特性曲线

从图8-图11可以看出，若将海底作为等效弹簧后，由于系缆刚度减小，单根系缆张力及系统恢复力均受影响。当系缆上端点移动相同位移时，缆1、缆2、缆4的张力均比原来减小，缆3张力比原来增大。当位移小于10 m时，这3根系缆张力变化并不明显，但是位移大于10 m时，张力变化幅度增大。系泊系统总水平恢复力与无海底影响时相比，先增大后减小。总垂直恢复力反而比原来小，其减小幅度也较为稳定，基本不随平台位移的变化而变化。

5 结 论

本文提出了平台主体沿x轴发生位移时，系泊系统静力特性的计算方法，同时指出在编程求解系泊系统恢复力时的注意事项，即在对系统进行某个位移点的恢复力计算时应考虑系统单根系缆是否处于松弛状态。文章对海底锚系点高度对单根系缆张力-位移特性的影响进行了论述，并且通过建立等效弹簧模型，对不同海底弹性基础的单根系缆张力及总系泊系统水平和垂直恢复力-位移特性进行研究，为绷紧式系泊系统的数值分析及理论研究奠定了一定的基础。后期将完善C++程序，完成其可视化界面，并投入现实使用。

［1］ 单日波.我国深水海洋油气田开发现状分析［J］.中国造船，2012（A1）： 274-278.

［2］ 黄维, 刘海笑.新型深水系泊系统非线性循环动力分析［J］.海洋工程，2010（2）： 22-28.

［3］ 赵晶瑞, 冯玮, 李迅科.深水多点系泊系统发展现状［J］.石油矿场机械，2013（5）： 1-7.

［4］ 易丛.Spar平台系缆张力及垂荡运动响应分析［D］.天津：天津大学，2007.

［5］ 唐友刚，易丛，张素侠.深海平台系缆形状和张力分析［J］.海洋工程，2007（2）： 9-14.

［6］ W.Raman-Nair，R.E.Baddour.Three dimensional dynamics of a flexible marine riser undergoing large elastic deformations ［J］.Multibody system dynamics，2003，10 ： 393- 423.

［7］ 王子寒.新型Spar平台方案设计和分析［D］.哈尔滨：哈尔滨工程大学，2012.

［8］ Wang H W，Luo Y，Hu K Y，et al.Mooring Truncation Design of a Deepwater SPAR ［J］.Journal of Marine Science and App1ication，2010（9）： 168-174.

［9］ 张火明，张晓菲，杨建民.基于优化思想的多成分系泊缆静力特性分析［J］.舰船科学技术，2010（10）：114-121.

［10］ 黄维.新型深水系泊系统非线性循环动力特性分析［D］.天津：天津大学，2009.

［11］ 潘斌，高捷，陈小红，等.浮标系泊系统静力计算［J］.重庆交通学院学报，1997（1）： 68-73.