波致立管疲劳损伤计算方法研究

朱东华

（中国人民解放军海军装备部 舰艇部 北京100841）

引 言

海洋工程中的立管结构是连接平台和海底管道或井口之间的主要设备，其所处的外部环境极为复杂，对波浪和海流的影响非常敏感，一直是石油工程研究领域的热点。控制立管的疲劳损伤是立管设计中的关键问题。［1］在稳定的波浪和海流作用下，引起立管产生疲劳损伤的主要因素有：立管自身在海流作用下的涡激振动以及与波浪引起立管上端浮体运动从而间接导致立管振动（即波致立管振动）。

国内外已有很多学者就立管涡激振动引起的响应特性以及引起的疲劳损伤进行了较深入的研究。Guo等人［2］研究了内部流体效应对立管涡激振动响应所产生的影响；Chaplin等人计算了剪切流中竖直张紧式立管的涡激振动响应；王一飞等人将深海立管简化细长张力梁模型，并分析疲劳损伤；周力等人［3］采用Orcaflex、Shear7等软件对深水中钢悬链式立管的涡激振动疲劳损伤进行分析；张建侨等人针对质量比对柔性立管涡激振动响应进行实验研究；高云等人［4］也对剪切流中SCR的涡激运动响应以及疲劳损伤进行相关研究。

此外，也有若干学者对波浪引起浮体运动而导致立管振动疲劳损伤进行研究。Sheehan等人［5］分别采用统计分析方法以及确定分析方法对柔性立管的波致疲劳损伤进行分析；黄维平等人采用ABAQUS软件对深水中顶张式立管的波致疲劳损伤进行分析；娄敏等人［6］运用相似理论将实际立管模型缩放为试验模型，从而测量立管的动力响应，并且与ANSYS有限元数值模拟结果进行比较。

钢悬链式立管是20世纪90年代初始提出的概念，经过十几年的发展，已成为深水开发的首选立管型式。从目前国内外的研究现状来看，针对钢悬链式立管的波致立管振动疲劳损伤的计算方法研究较少。

基于以上原因，本文对波浪引起浮体运动所导致的波致立管振动疲劳损伤进行相关分析。在分析过程中，先是采用势流理论对波浪引起的平台运动响应进行分析，得到平台的运动频响函数；接着采用有限元法对立管进行应力响应分析，得到立管的应力频响函数；最后结合立管材料S-N曲线，采用谱分析方法对四种海况下的波致立管振动疲劳损伤进行分析。［7］

1 基本理论

1.1 平台运动响应理论

分析波浪上平台运动响应的过程中作如下假定：

（1）流体假定。假定流体是没有粘性的理想流体，同时认为流体是无旋有势、均匀不可压缩。

（2）刚体假定。假定平台是刚体，在外力作用下不变形。这样就有速度势存在，建立OXY平面为静水平面、Z轴垂直向上的右手坐标系，由控制方程、边界条件可得到以下方程：

通过格林函数法得到速度势后，流体的动压力可表示为：

若流场中压力p已知，则作用于平台的外力可表示为：

经计算整理得到，平台的运动表达式为：

式（8）实际上是一个复系数的线性代数方程组，从中可解出平台的运动响应，它是复数，既含有相位又含有运动的幅值。式（8）的求解实际上是固定频率下代数方程的求解，即平台的运动响应频率响应函数。

1.2 立管疲劳损伤理论

假设系统为稳定系统，即有以下表达式：

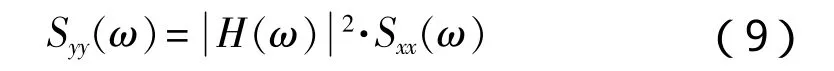
假设立管受到的应力为一个平稳随机过程，设应力峰值为S的概率密度为p（S），则在带宽dS内应力峰值达到S的循环次数n（S）为vTp（S）dS，其中，v为双边超越概率，对于双边跨越平稳的高斯随机过程，v可表示为：

式中：m0与m2分别为应力谱的零阶矩和二阶矩，可表示为应力谱的相关函数：

假设疲劳损伤过程满足窄带高斯随机过程，D表示一年内立管的年疲劳损伤率，则可表示为:

2 数值算例

2.1 计算模型

本文计算的平台为Spar平台，在实际计算中，可将其简化为一个尺度大、吃水深、直立悬浮的刚性圆柱体，沿x、y、z轴有3个平动自由度，分别为纵荡、横荡以及垂荡，如图1所示。本文定义从x轴负方向传来波浪的浪向角θ为0°，从x轴正方向传来波浪的浪向角θ为180°。

图1 浪向角定义

本文计算的是与Spar平台相连接的钢悬链式立管的波致振动疲劳损伤，立管的参数如表1所示。

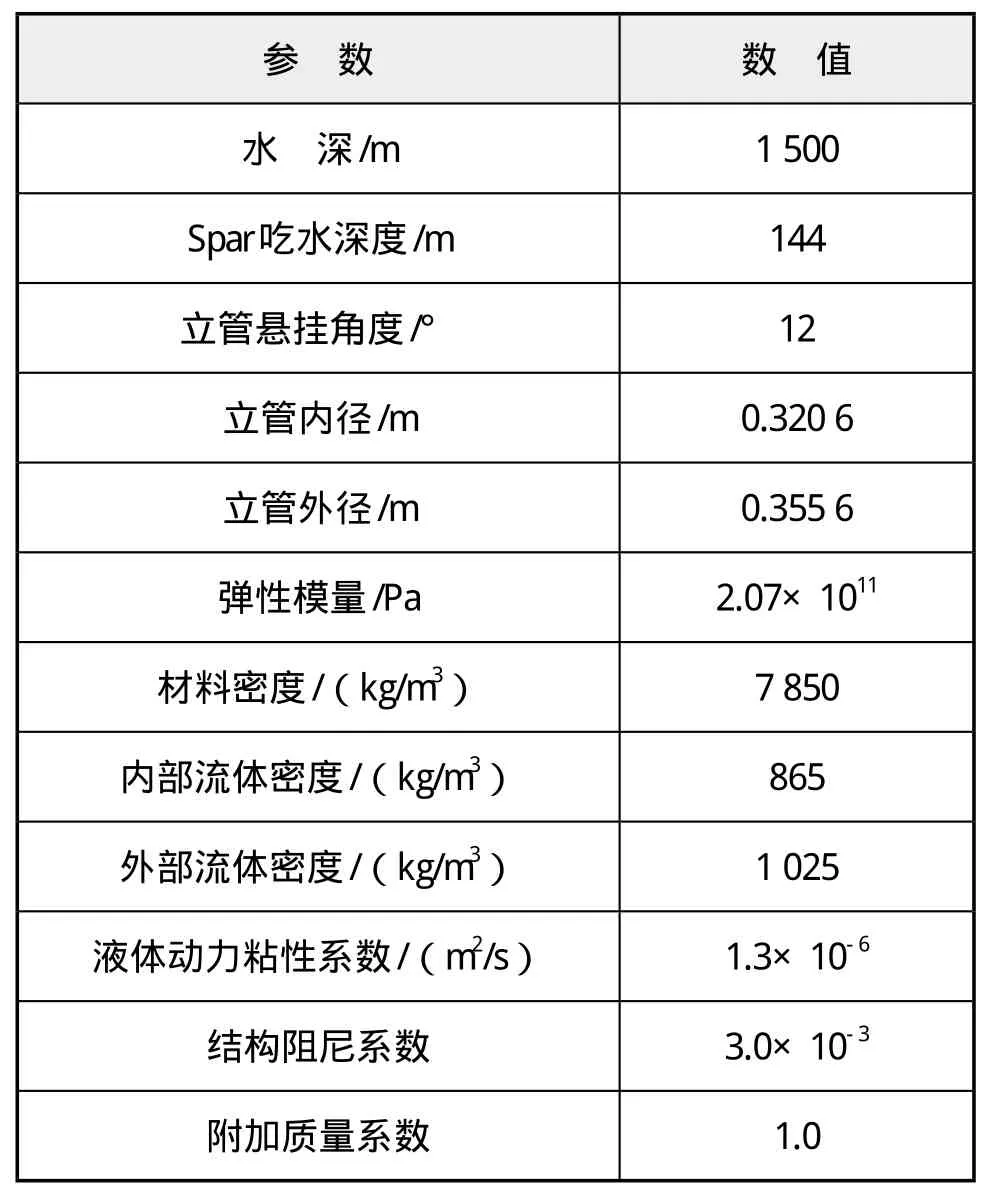
表1 立管基本参数

计算过程中采用的S-N曲线为DOE-E，采用的波浪谱为ITTC单参数谱，表达式如下：

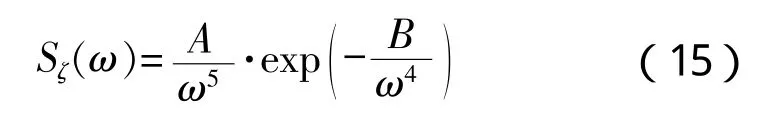
式中：A= 8.10×10-3×g2= 0.78；B= 3.11/（h1/3）2，h1/3为波浪谱的有义波高。本文对有义波高分别为1 m、2 m、3 m以及4 m的波浪谱进行波致疲劳损伤计算。

2.2 平台及立管的频响函数

采用第1.1节所述的相关理论，通过编程计算对平台运动频响函数进行了分析，对于纵荡（Surge）以及垂荡（Heave）运动的频率响应函数的计算，采用0°浪向角；对于横荡（Sway）运动的频响函数的计算，采用180°浪向角。图2-图4依次给出3个平动自由度方向的频响函数。

图2 纵荡频响函数

图3 垂荡频响函数

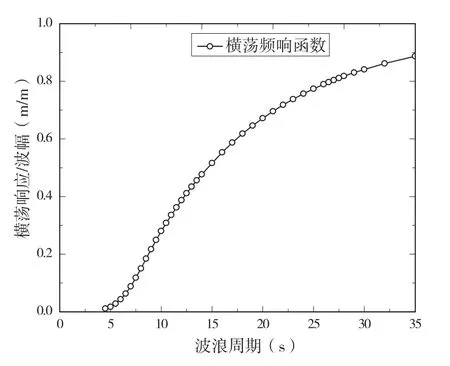
图4 横荡频响函数

对于立管应力频响函数分析，是利用有限元法进行的，在有限元软件ANSYS中建立立管模型。由于本文计算的立管L/D远大于200，所以采用的单元为PIPE59索单元模型。

在立管上端与平台的连接点（即悬挂点）施加一个单位幅度的谐振运动，运动幅度为1 m，运动频率从0～4 Hz。运动方向分别为：纵荡方向、横荡方向以及垂荡方向。从触地点到悬挂点，将立管均匀分成1 000个单元，单元编号依次从1号至1 000号递增。图5-图7分别给出平台在3个平动自由度方向的立管1号、100号、…1 000号单元的应力频响函数。

图5 纵荡方向的应力频响函数

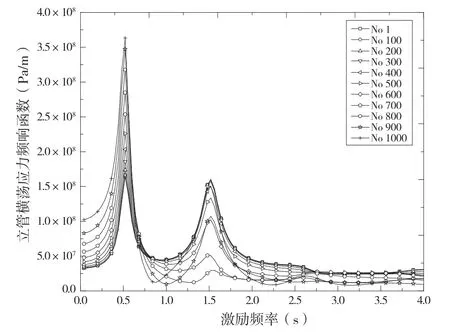
图6 横荡方向的应力频响函数

图7 垂荡方向的应力频响函数

得到平台的运动频响函数以及立管的应力频响函数后，可根据谱分析理论计算得到波致立管振动疲劳损伤，本文对3个平动自由度（纵荡、横荡以及垂荡）引起的疲劳损伤分别进行分析。假设建立垂直向上的坐标系，设海底接触点处的坐标为0，上端悬挂点的坐标为1，即可得到立管的相对位置坐标。图8-图10依次给出4种海况下纵荡、横荡以及垂荡引起的疲劳损伤。

2.3 疲劳损伤分析

如图2-图10所示，分别给出平台的运动频响函数以及立管的应力频响函数，最后采用谱分析方法得到了波致立管振动疲劳损伤，综合分析上述图形，可以得出如下结论：

图8 立管纵荡方向年疲劳损伤率

图9 立管横荡方向年疲劳损伤率

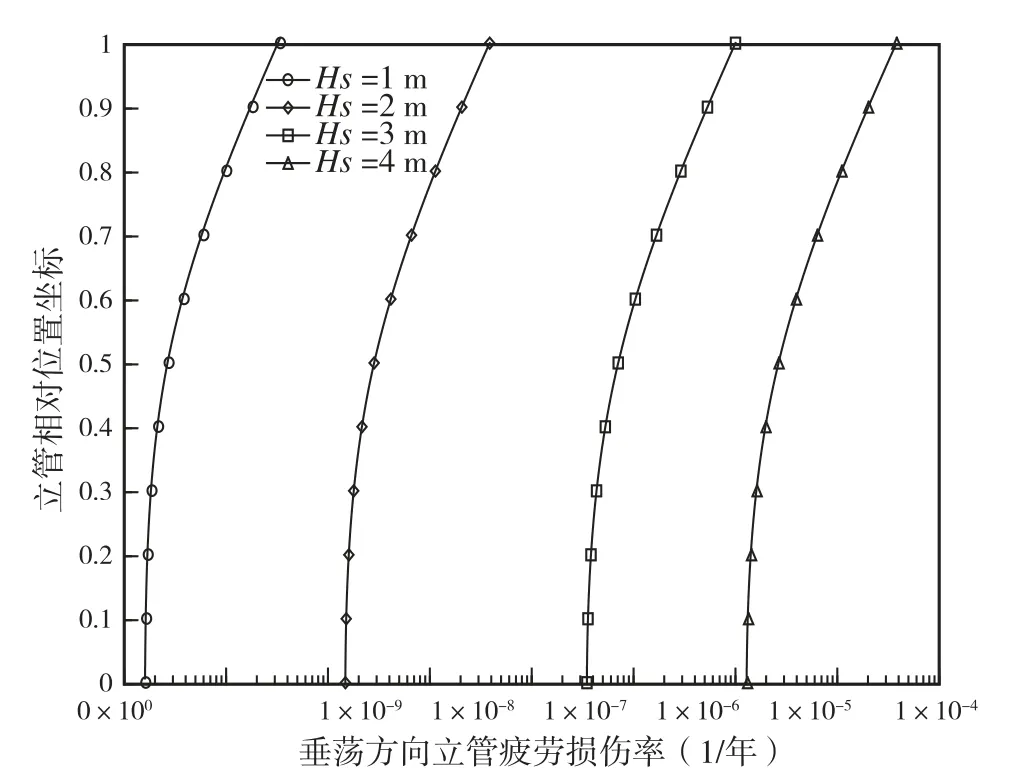
图10 立管垂荡方向年疲劳损伤率

（1）由于Spar平台的对称特性，因此平台的纵荡频响函数和横荡频响函数具有相同的变化规律。但是，由于钢悬链式立管的不对称特性，在分析波致立管振动疲劳损伤时，纵荡和横荡将引起不同大小的立管疲劳损伤，应该分开加以考虑和分析。

（2）由立管的应力频响函数曲线可以得知：立管的应力最大响应出现了几个峰值，分别发生在激励频率为0.5 Hz、1.5 Hz、2.7 Hz以及3.8 Hz等固有频率处。

（3）由波致立管振动疲劳损伤率可以看出，立管的波致损伤大小与海况紧密相关，且随着有义波高的增加而成指数次方增长。

3 结 论

本文主要对波浪引起浮体运动所导致的波致立管振动疲劳损伤进行相关分析。得知波浪周期的变化会对平台的运动频响函数和立管的应力频响函数产生不同的影响，特别是在垂荡方向上会出现明显的峰谷波动，因此在海洋工程产品设计和应用中，应采取合理的措施规避不利的激励频率。

另外，不同立管位置和不同有义波高产生的波致立管损伤存在一定程度的差异，因此，在设计中应对立管中疲劳损伤严重的部位采取适当的加强措施，并根据平台作业海域的长期有义波高统计值进行立管抗疲劳损伤的结构设计。

［1］ 周巍伟.深海悬链线立管涡激疲劳损伤预报研究［D］.大连：大连理工大学，2009.

［2］ Guo H Y，Lou M.Effect of internal flow on vortex induced vibration of risers ［J］.Journal of Fluids and Structures，2008，24: 496-504.

［3］ 周力，周巍伟，曹静，等.深海悬链线立管涡激疲劳损伤研究［J］.海洋工程，2010，28（1）: 36-41.

［4］ 高云，宗智，周力，等.钢悬链式立管涡激振动疲劳损伤分析［J］.中国舰船研究，2010，5（5）: 54-58.

［5］ Sheehan J M，Grealish F W，Harte A M et al.Characterizing the wave environment in the fatigue analysis of flexible risers［C］.In: Proceedings of the 24th International Conference on Offshore Mechanics and Arctic Engineering，2005.

［6］ 娄敏，董文乙，郭海燕.波浪作用下海洋立管试验研究及ANSYS数值模型 ［J］.中国造船.2010，51（1）:73-77.

［7］ 高云.钢悬链式立管疲劳损伤分析 ［D］.大连：大连理工大学，2011.