稳定控制研究中的多机电力系统数学模型

2014-01-03彭叙

电子测试 2014年2期

彭叙

（锦州市机电工程学校,辽宁锦州,121013）

1 稳定控制研究工作中多机电力系统数学模型的组成要素

1.1 同步发电机数学模型的分类

在电力系统的研究中，由于与电相关，所以一定要从正、负电荷两个方面去考虑，在电力系统的研究中负电荷一般规定为恒定不变的阻抗，所以电力系统数学模型的研究主要以正电荷的研究为主，正电荷的主要来源就是电力系统的同步发电机。同步发电机的数学模型多种多样，笔者在此简单对其进行了分类：

（1）经典模型：这种模型主要研究的状态是暂时动态电抗以后的电势；

（2）E′q 模型：这种模型是建立在忽略阻尼绕组的基础上；

（3）双轴模型：这种模型的建立主要是针对实心转子电机而言的，在电机工作的时间候要忽略∮d 和∮q；

（4）Park 模型：这种数学模型与E′q 模型是对立的关系，它要考虑磁场和阻尼绕组对电机工作的影响；

（5）E′′模型：这种模型与经典模型是承接关系，它主要研究的是次暂态电抗后的电压；

（6）单轴模型：与双轴模型不同的是，单轴模型的建立要忽略阻尼效应和∮d 和∮q。

从整体上讲，以上这六种模型各有各的实用特点，但是为了方便快捷，在电力系统稳定控制的研究工作中，往往会建立经典模型。除了单轴模型偶尔会用在磁链衰减的状态研究中，其它几种模型由于较为复杂，微分方程不易计算，往往只能在数学仿真中得到一定的应用。

1.2 参考轴

多机电力系统的稳定性是一个需要全面考虑的问题，这和决定它的因素——发电机转子之间的角度差有着不可分割的关系，但是电力系统的稳定性不能单纯只靠转子与电压之间的相位差来表示，参考轴的建立也是非常有必要的。在多机电力系统中建立参考轴，根本目的就是为了确定转子的相对位置，进而获得多转子之间的角度差。不同的参考轴对应不同的数学模型，总体上说参考轴分为MOF：以电机转子为中心建立的参考轴；SF：同步旋转参考轴；CAF：以惯性为中心建立的参考模型。

1.3 数学模型建立后的使用

在一个电力系统的数学模型建立完成之后，如何运用它对电力系统的稳定性进行控制是一个关键性问题。使用数学模型之前，需要准确掌握系统当下以及理想的状态，只有这样，才能在数学模型的理论基础上更好的控制系统以达到理想的动态平衡状态。

2 多机电力系统经典模型

经典模型在多级电力系统稳定性控制工作中被广泛的建立以及使用，它的建立需要以下几个假定条件：

（1）负电荷需要给予相应的表示，无源阻抗在此用来表示负电荷；

（2）机械输入的功率不需要变化，要保持恒定；

（3）电机的暂时动态电抗之后产生的电势角的角度要与机械转子角的角度保持一致；

（4）电机的暂时动态电抗之后产生的电势不仅对多机电力系统有效，对同步电机也是有效的。

假设一个电力系统有n 个发动机，从这些发动机的发动端点向发动机内部的网络看，我们可以得到一个I=YE 的导纳阵列。在这个导纳阵列中，Y 包含两种元素——对角线以及非对角线元素。Y 的对角线元素为每个电压节点i 的输入部分的导纳；而Y的非对角线元素为每个空间电压节点i 和j 的转移导纳的负数值。

所以，多级电力系统的经典模型的建立如下图所示：

在该经典模型中，节点i 的输出功率由下面这个式子进行表达：

3 多机电力系统观测解藕状态空间模型

由于多级电力系统数学模型建立的终级目标是更好的控制系统的稳定性，所以如何使用最快、最便捷的方法确定一个电机的具体空间位置，进而获得对电机更好的控制权，是电力领域的学者一直在深入研究的问题。美国电力学家托马斯在经过长期实验之后，得出了一种通过局部看整体的观测解藕状态空间模型，这种空间模型建立的前提条件是所研究的第i 台电机的数学模型要非常完整。空间模型如下图所示。

多机电力系统观测解藕状态空间模型如下图所示：

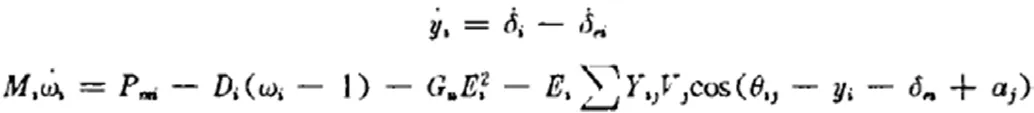
其中，平衡状态可以用以下方程组表示：

在多机电力系统观测解藕状态空间模型的建立过程中，要注意：δi 和αi 的数值的得出虽然需要通过θi，但是yi 和θi却已经没有了任何关系，它们关系的转变与该数学模型的第一个公式有很大的关系。托马斯在经过大量的实验得出结论，如果在多机系统的每一个组成电机都处在理想稳定的平衡点的时候，那么整个电力系统都可以称作稳定状态。多机电力系统观测解藕状态空间模型的实用点就在于，只要控制好每一个子系统，那么整个系统的稳定性就可以被很好的控制了。