考虑应力敏感与非达西效应的页岩气产能模型

田 冷 肖 聪 顾岱鸿

1.中国石油大学石油工程教育部重点实验室 2.中国石油大学（北京）石油工程学院

页岩气藏是典型的非常规气藏［1－2］，在储层中存在解吸、扩散和渗流相互作用，因而，其在渗流机理和流动方式上都有异于常规油气藏，国内外许多学者对页岩气渗流规律及其产能模型进行了研究［3－4］。Barenblatt提出页岩气双孔模型［5］，但未考虑页岩气解吸和扩散影响；El－Banbi提出线性双孔模型［6］，首次给出拉普拉斯空间解，但忽略页岩气解吸和扩散影响；Ah－Ahmadi等给出了考虑页岩气解吸和扩散影响的三孔线性流模型［7］，但没有考虑微裂缝应力敏感的影响；赵玉龙、张烈辉等给出了页岩气拟三孔球形流模型［8］，考虑页岩气解吸扩散影响，但考虑人工裂缝为无限导流裂缝，忽略了人工裂缝中非线性流和微裂缝中的应力敏感效应影响；蔡华等在传统裂缝—基质双重介质模型基础上，建立了考虑裂缝应力敏感效应的页岩气产能模型［9］，但仅局限于对直井，并且没有考虑高速非达西流的影响；王海涛等给出了页岩气双孔球形流模型［10］，考虑页岩气解吸扩散和微裂缝中的应力敏感效应影响，但考虑人工裂缝为无限导流裂缝，忽略了人工裂缝中非线性流。

笔者简化压裂地层为块状模型，建立考虑天然裂缝应力敏感和人工裂缝非达西渗流的数学模型，应用全隐式有限差分和牛顿—拉普森迭代法进行数值求解，绘制了页岩气产量递减曲线，并分析了相关因素对气井产量递减规律的影响。

1 产能模型建立

页岩气多级压裂地层简化为块状模型，考虑矩形封闭地层中心1口水平井定压力生产，其他条件做如下假设：①在初始条件下，地层各处的压力为pi，储层具有双孔介质特征；②人工裂缝垂直于井筒，关于井筒对称且均匀分布，人工裂缝条数为n且完全贯穿储层，天然裂缝与人工裂缝垂直，气藏的长、宽分别与水平段和裂缝等长；③人工裂缝有限导流能力，考虑人工裂缝非达西流动和天然裂缝应力敏感效应；④仅人工裂缝向井筒供气，只考虑气体从基质向天然裂缝的线性流动，忽略气体从基质向人工裂缝和井筒的流动；⑤页岩气微可压缩，压缩系数恒定；⑥页岩气解吸满足Langmuir等温吸附方程，扩散满足Fick第一定律；⑦忽略重力和毛细管力的影响。

1.1 应力敏感效应

考虑气体拟压力形式下的应力敏感对渗透率影响可以表述为：

式中K为考虑应力敏感的地层渗透率，D；Ki为原始地层渗透率，D；Ψi为原始地层拟压力，MPa2／（mPa·s）；β为应力敏感系数，（mPa·s／MPa2）；Ψ 为地层拟压力，MPa2／（mPa·s）。

1.2 非线性流动效应

Forcheimer建议用二次流动项来描述非线性流动：

引入非达西流动效应修正系数（δ），则达西定律修正方程表示为：

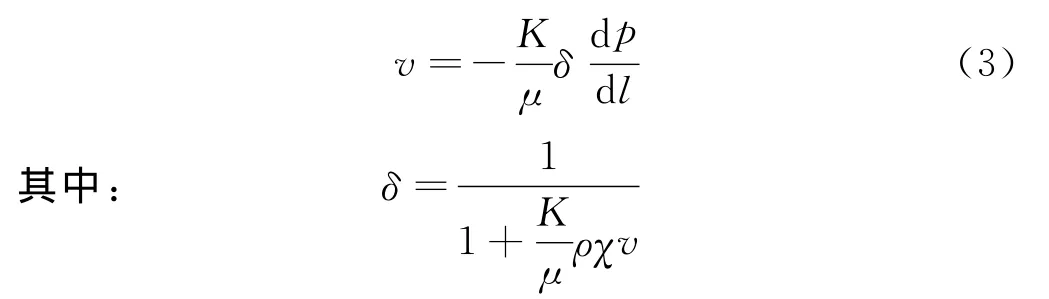
式中K为地层渗透率，D；p为地层压力，MPa；μ为气体黏度，mPa·s；ρ为气体密度，kg／m3；δ 为非达西流动效应修正系数；v为渗流速度，m／s；χ为非达西系数，μm0.6；l为长度，m。

1.3 吸附效应

目前主要运用兰格缪尔等温吸附方程来描述页岩气吸附、解吸过程，其表达式为：

式中VE是平衡吸附浓度，m3／m3；VL是兰格缪尔吸附浓度，m3／m3；pL是兰格缪尔压力，MPa；ψL是兰格缪尔拟压力，MPa2／（mPa·s）。

1.4 数学模型

考虑页岩气在储层中解吸扩散气体从基质到天然裂缝为拟稳态窜流，天然裂缝到人工裂缝为不稳定窜流，由质量守恒定律分别得到基质、天然裂缝和人工裂缝中流动方程。

1.4.1 人工裂缝

式中Ψj分别为人工裂缝、天然裂缝和基质的拟压力，MPa2／（mPa·s），j＝F，f，m；x、y分别为距离，m；μ为气体黏度，mPa·s；φj分别为人工裂缝孔隙度、天然裂缝孔隙度和基质孔隙度，小数，j＝F，f，m；（Ct）j分别是人工裂缝、天然裂缝和基质系统的综合压缩系数，MPa－1，j＝F，f，m；Kf、Kfi、Km分别为人工裂缝渗透率、天然裂缝渗透率和基质渗透率，D；t为时间，h；psc为地面标准状况下的压力，MPa；T为储层温度，K；Tsc为地面标准状况下的温度，K；α是基质岩块形状因子，m－2；Lf为人工裂缝之间的距离，m。

1.4.2 天然裂缝

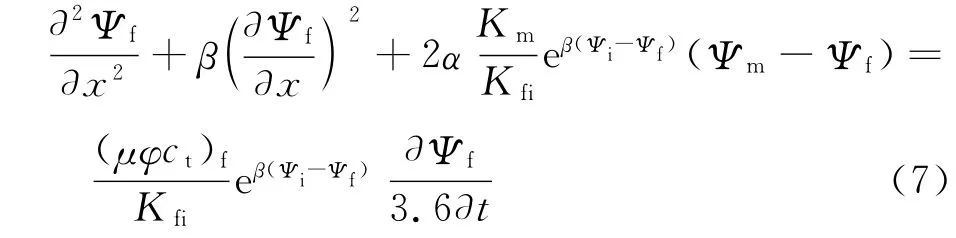
1.4.3 基质

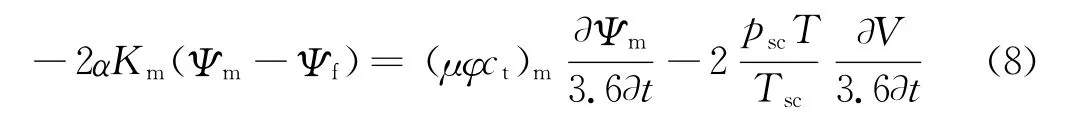
由菲克第一定律得到，气体向基质中的扩散速度可以表示为：

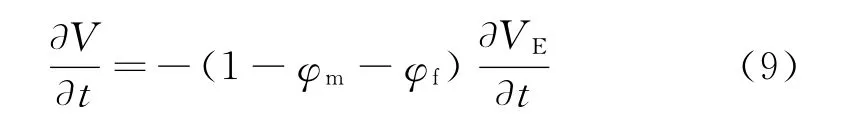
式中V为页岩气浓度，m3／m3。

带入兰格缪尔等温吸附方程可以得到：

2）无因次时间

3）无因次应力敏感系数

5）无因次储容比

6）裂缝导流能力比

7）无因次初始拟压力

8）无因次兰格缪尔拟压力

9）无因次兰格缪尔体积

10）无因次产量

11）无因次距离

式中Acw为井筒流动面积，Acw＝2LFh，m2；LF为井筒长度，m；h为地层厚度，m；ye是人工裂缝长度，m。

将式（6）～式（8）及边始条件式无因次化后得到以下方程。

1）人工裂缝

2）天然裂缝

初始条件：

根据无因次产量与无因次拟力的关系，可以得到：

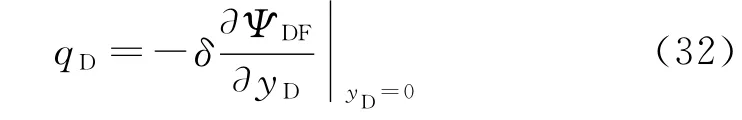
2 产能方程求解

2.1 网格划分

方程式（21）、（25）、（29）是关于拟压力的强非线性偏微分方程，难以求出其解析解。因此采用数值解法，利用全隐式有限差分法将其进行离散。

对模型做进一步假设：人工裂缝沿水平井筒均匀分布，所有人工裂缝等效，并且不考虑裂缝之间的干扰。取其中一个流动单元（图1）进行分析，并对其进行网格划分（图1）。

图1 流动基本单元及其离散示意图

人工裂缝、天然裂缝和基质离散分别遵循以下原则：①人工裂缝中近井筒附近压降大，非达西效应严重，故将其细分，取较小的步长，而在远离井筒地带，由于高的人工裂缝导流能力，可以粗化其模块，取较大步长；②天然微裂缝考虑应力敏感效应，缝内压力分布差异大，步长应适当选取，以满足精度要求；③基质向微裂缝拟稳定窜流，压力处处相等，便于处理，将基质离散为与微裂缝相同的单元数。

2.2 方程离散

由于偏微分方程中存在非达西流动修正系数（δ），同时δ也是压力的函数，我们已经知道人工裂缝具有高导流能力。因此一定时间差内，缝内压差并不大，可以利用前一时间的缝内压力分布迭代求解的δ作为本次的δ参与求解。将式（22）～式（32）运用全隐式有限差分法离散后的方程如下所示。

2.2.1 人工裂缝

2.2.2 天然裂缝

2.2.3 基质

2.2.4 边界和初始条件

对于式（30）～式（33），利用牛顿拉普森迭代法进行数值求解。

3 典型曲线绘制及因素分析

通过有限差分和牛顿迭代法获得无因次产量（qD）随无因次时间（tD）的变化关系，并做出各种因素影响下的产量qD－tD和产量导数qD－tD双对数图版。对典型曲线（图2）分析得到4个流动阶段：①阶段Ⅰ——人工裂缝线性流阶段。产量导数曲线斜率为－1／2，为前期人工裂缝中线性流阶段。②阶段Ⅱ——双线性流阶段。产量导数曲线斜率为－1／4，为人工裂缝和微裂缝中双线性流阶段。③阶段Ⅲ——窜流阶段。产量导数曲线出现“凹”形，此时为基质向微裂缝的拟稳定窜流阶段。④阶段Ⅳ——边界控制流阶段。此时边界已经对生产动态产生影响，产量和产量导数曲线迅速下降，出现边界控制阶段。

图2 典型曲线及流动阶段划分示意图

3.1 应力敏感效应

文中考虑微裂缝中的应力敏感效应，图3表明：应力敏感对前期几乎没有影响，其主要影响微裂缝中的流动阶段，也就是窜流及其后流动阶段。随着应力敏感系数的增大，无因次产量和产量导数曲线整体下移，分析其机理可知，裂缝压力降低，裂缝发生闭合，渗透率降低，气体流动渗流阻力增大，从而使产能减小。

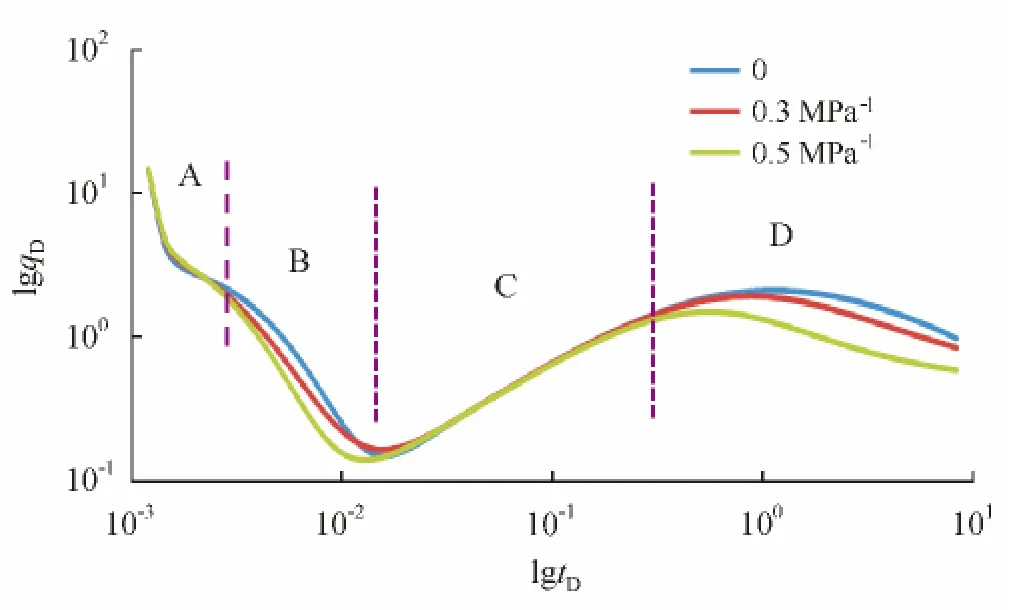
图3 不同应力敏感系数的典型曲线图

图3中A和B阶段应力敏感效应显著，而A、C阶段应力敏感较弱。分析其机理为：A阶段主要是人工裂缝线性流阶段，此时裂缝中压力并没有降低，应力敏感效应并没有发生；B阶段为天然裂缝中线性以及基质向裂缝窜流前期阶段，此时窜流量不足以弥补裂缝中的亏空量，导致压力降低，应力敏感效应显著发生；C阶段为窜流后期，由于解吸发生，窜流量能够很好地补充亏空量，裂缝压力基本没有下降，应力敏感效应消失；D阶段为边界控制流阶段，流动到达边界后，无外来流体补充，裂缝中压力降低，此时应力敏感影响显著。

3.2 非达西效应

人工裂缝中非达西效应的影响主要通过非达西修正系数（δ）是否等于1来体现，图4给出了考虑和不考虑非达西效应下的无因次产量及其导数典型曲线，分析可知：高导流能力人工裂缝中，非达西效应影响显著，考虑非达西效应时，曲线整体下移，这是由于附加阻力的存在，导致渗流能力降低，产能下降。

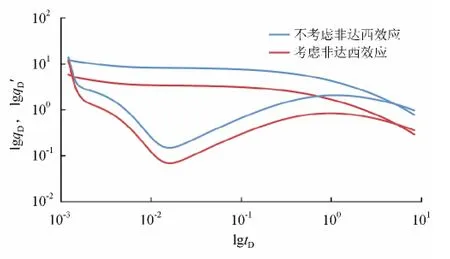
图4 考虑非达西效应影响典型曲线图

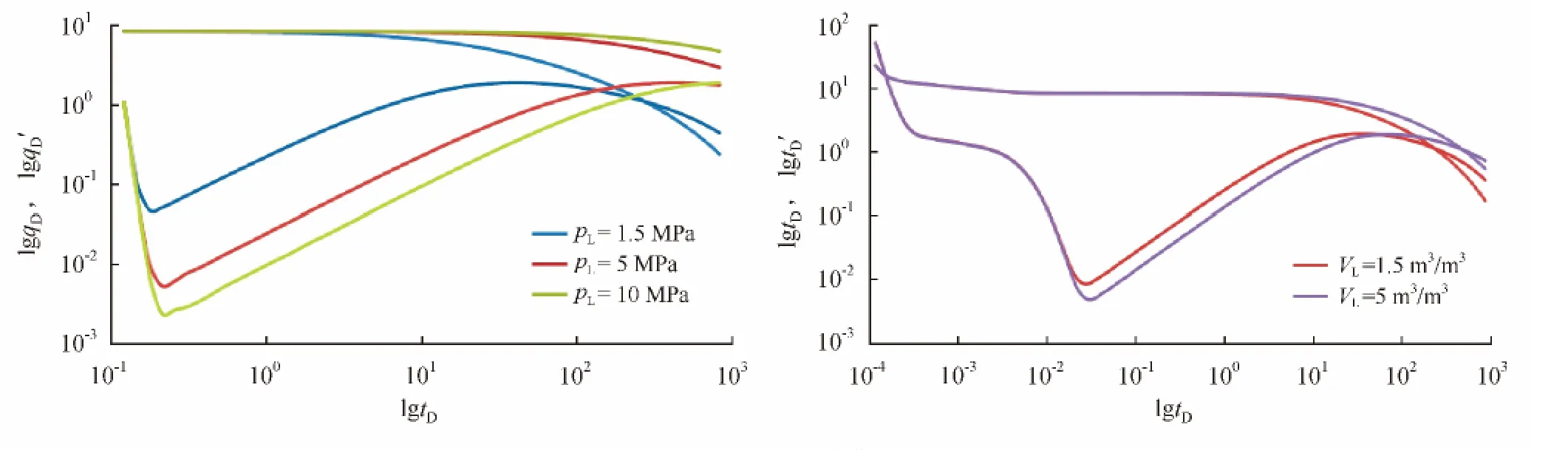
图5 兰格缪尔参数影响典型曲线图

3.3 吸附效应

页岩气吸附效应中最重要的两个特征参数就是兰格缪尔压力和兰格缪尔体积，通过分析绘制的典型曲线图版（图5）可以得到，pL和VL主要是影响窜流阶段以及产量衰减出现的早晚，pL越大（pL取1.5MPa、5MPa和10MPa）窜流阶段出现得越晚，产量越晚出现衰减；同时，VL越小（VL取1.5m3／m3、5m3／m3）窜流阶段出现得越早，产量越早出现衰减。

从微观机理分析，随着兰格缪尔体积和兰格缪尔压力增大，吸附气含量增大，随压力降低，基质中的吸附气向裂缝中解吸扩散，使得裂缝中压力降落速度减慢，所需时间延长，从而窜流阶段出现的时间向后延迟，出现图中“凹”形向右移的现象。同时，由于基质中页岩气解吸，补充了气体的亏空，使得压力降低缓慢，封闭边界的影响较小，当页岩气解吸达到一定程度后，解吸量不足以弥补边界的影响，产能开始显著降低，边界控制流动阶段显著发生。

4 结论

1）建立了考虑应力敏感和非达西效应、页岩气吸附、解吸产能模型，运用数值方法绘制典型曲线，并对其产能影响因素进行了分析。

2）通过对典型曲线的分析，页岩气流动分为4个阶段：人工裂缝中的线性流阶段；人工裂缝和天然裂缝中的双线性流阶段；基质向天然裂缝中的窜流阶段；气藏边界控制流动阶段。

3）考虑天然裂缝中的应力敏感效应，由于页岩气解吸，窜流以及边界控制的影响，天然裂缝中应力敏感效应阶段性发生，其中在天然裂缝双线性阶段，窜流前期阶段以及后期边界控制流阶段，应力敏感显影显著发生，并且应力敏感系数越大，无因次产量导数曲线下移量越多，产能降低越显著。

4）高导流能力人工裂缝中非达西效应显著发生。考虑非达西效应时，产量导数曲线前期下降。因此，在实际气藏开发中不能忽视非达西效应的影响，尤其是对于高生产压差气井。

5）分析表征页岩气吸附特性的两个特征参数——兰格缪尔压力和兰格缪尔体积，得知两者主要影响窜流阶段以及边界控制流阶段发生的早晚。

［1］王世谦.中国页岩气勘探评价若干问题评述［J］.天然气工业，2013，33（12）：13－29.WANG Shiqian.Shale gas exploration and appraisal in China：Problems and discussion［J］.Natural Gas Industry，2013，33（12）：13－29.

［2］姜呈馥，程玉群，范柏江，等.陆相页岩气的地质研究进展及亟待解决的问题——以延长探区上三叠统延长组长7段页岩为例［J］.天然气工业，2014，34（2）：27－33.JIANG Chengfu，CHENG Yuqun，FAN Bojiang，et al.Progress in and challenges to geological research of terrestrial shale in China：A case study from the 7thmember of the Upper Triassic Yanchang Fm in the Yancheng exploration block，Ordos Basin［J］.Natural Gas Industry，2014，34（2）：27－33.

［3］杨程博，郭建春，杨建，等.低渗气藏水平井二项式产能方程修正［J］.西南石油大学学报：自然科学版，2014，36（4）：123－130.YANG Chengbo，GUO Jianchun，YANG Jian，et al.Modification of horizontal well binomial deliverability equation of low permeability gas reservoir［J］.Journal of Southwest Petroleum University：Science ＆ Technology Edition，2014，36（4）：123－130.

［4］程远方，李友志，时贤，等.页岩气体积压裂缝网模型分析及应用［J］.天然气工业，2013，33（9）：53－59.CHENG Yuanfang，LI Youzhi，SHI Xian，et al.Analysis and application of fracture network modes of volume fracturing in shale gas reservoirs［J］.Natural Gas Industry，2013，33（9）：53－59.

［5］BARENBLATT G I，ZHELTO I P，KOCHINA I N.Basic concepts of the theory of seepage of homogeneous liquids in fissured rocks［J］.Journal of Applied Mathematical Mechanics，1960，24（5）：852－864.

［6］El－BANBI A H.Analysis of tight gas well performance［D］.Texas A＆M University，1998.

［7］AL－AHMADI H A，WATTENBARGER R A.Triple－porosity models：One further step towards capturing fractured reservoir heterogeneity［C］∥paper 149054－MS presented at the SPE／DGS Saudi Arabia Section Technical Symposium and Exhibition，15－18May 2011，Al－Khobar，Saudi Arabia.New York：SPE，2011.

［8］ZHAO Yulong，ZHANG Liehui，ZHAO Jinzhou，et al."Triple porosity"modeling of transient well test and rate decline analysis for multi－fractured horizontal well in shale gas reservoirs［J］.Journal of Petroleum Science and Engineering，2013，110：253－262.

［9］蔡华，付随艺，程时清.裂缝性页岩气藏考虑应力敏感的产量递减模型构建［J］.科技导报，2013，31（24）：51－54.CAI Hua，FU Suiyi，CHENG Shiqing.Production decline mode for fractured shale gas reservoirs with stress sensitivity［J］.Science ＆ Technology Review，2013，31（24）：51－54.

［10］WANG H T.Performance of multiple fractured horizontal wells in shale gas reservoirs with consideration of multiple mechanisms［J］.Journal of Hydrology，2014，5（10）：299－312.