超大跨度斜拉桥空气静力和动力稳定性研究
2014-01-02张新军孙海凌
张新军,孙海凌
(浙江工业大学,杭州 310014)
1 前言
从1956年德国工程师迪辛格研究设计了第一座现代斜拉桥——瑞典的斯特洛姆桑特桥起,斜拉桥以其跨越能力的优势和良好的受力性能得到了飞速的发展,香港昂船洲大桥和苏通长江大桥分别以1 018m和1 088m的主跨实现了斜拉桥跨度千米级的突破,紧随其后俄罗斯的主跨1 104m的海参威Russky岛大桥也于2012年7月建成。当前,世界桥梁工程正进入跨海联岛工程建设的新时期,斜拉桥的跨径仍在继续增大。世界上主要是在亚洲,还有多座大跨度斜拉桥正在规划中,其中不乏有主跨超过1 000m的超大跨度斜拉桥,如韩国计划在东南部的马山市和Geoje岛的连岛工程中采用主跨1 200 m的斜拉桥方案、日本本四联络线的主跨1 400m的斜拉桥方案等。由于斜拉桥在刚度、抗风性能、斜拉索可更换、施工简便、无锚碇等方面的优越性,在近年来的国际跨海大桥方案竞赛中,斜拉桥方案都优于悬索桥而被采用,斜拉桥已成为当代大跨度桥梁的主流桥型[1]。斜拉桥极限跨度的研究也表明:1 200m以下是比较合适的区域,1 200~1 500m斜拉桥仍具有竞争力[2,3]。
随着斜拉桥跨径的持续增大,结构更加轻柔,结构的弯曲和扭转刚度随之降低,风作用下结构的稳定性问题已成为影响和控制其设计的主要因素。结构的抗风稳定性包括静力风荷载和动力风荷载作用下结构的稳定性,前者主要指静风扭转发散或横向屈曲失稳,而后者则主要指颤振稳定性。迄今为止,国内外学者对跨径在千米及以下的斜拉桥开展了比较系统的抗风研究,但对于超千米以上更大跨径斜拉桥的抗风性能研究则非常少。Nagai等对1 400m主跨的钢斜拉桥进行了设计和分析,并进行了不同主梁宽度和高度情况的空气静力和动力稳定性的选型分析[4,5]。Kao等对采用碳纤维索的1 400m主跨斜拉桥进行了静风作用下的结构稳定性分析,从抗风稳定性角度探讨了碳纤维索在超大跨度斜拉桥中应用的可能性[6]。Kien等对主跨1 200~1 800m范围内的超大跨度斜拉桥进行了风作用下的静力和动力稳定性分析,探讨了斜拉桥在超千米以上桥梁上应用的可能性及其极限跨径[7]。孙斌开展了1 400m主跨的全自锚斜拉桥、部分地锚斜拉桥和协作体系桥的设计,并进行了恒载和极限静风荷载作用下的结构反应分析和比较[8]。
可以看出,前期研究主要对超千米跨度斜拉桥进行了抗风稳定性的分析,并从抗风性能角度探讨斜拉桥在超大跨度桥梁中应用的可能性,但对结构设计参数对主跨超千米以上的超大跨度斜拉桥抗风稳定性的影响研究则基本没有涉及,因此不能很好地指导超大跨度斜拉桥的抗风设计。为此,本文针对一主跨1 400m的超大跨度斜拉桥设计方案,采用大跨度桥梁三维非线性空气静力和动力稳定性分析方法,对其抗风稳定性进行了分析,并与同等主跨的悬索桥进行了对比,从抗风性能角度探讨了斜拉桥在超千米主跨桥梁中应用的合理性。在此基础上,分别就主梁的高度和宽度、桥塔结构型式、桥塔高跨比、边主跨比、辅助墩设置、斜拉索锚固方式等结构设计参数对超大跨度斜拉桥空气静力和动力稳定性的影响进行了分析,指出了关键的设计参数及其合理取值,以期为超大跨度斜拉桥的抗风设计提供依据。
2 桥梁简介
图1为一主跨1 400m的超大跨度斜拉桥设计方案[2],桥跨布置为680m+1 400m+680m,边跨端部设置间距为100m的3个辅助墩以提高结构的整体刚度。A形桥塔高约327m,采用全钢结构,其中桥面以上高度约287m。斜拉索在桥面主梁上的锚固间距为20m,在桥塔上的锚固间距为4m,全桥共设置4×34对斜拉索。桥面主梁采用扁平状流线型钢箱梁,宽35m,高3.5m。为了确保桥梁的稳定性和侧向抗风性能,在桥塔两侧各80m范围内对桥面主梁进行了截面加强。

图1 主跨1 400m斜拉桥设计方案(单位:m)Fig.1 Design alternative of a cable-stayed bridgew ithmain span of 1 400m(unit:m)
3 超大跨度斜拉桥抗风稳定性的分析与比较
3.1 空气静力稳定性
本文采用大跨度桥梁三维非线性空气静力分析程序[9],在0°风攻角下,对设计方案桥进行了非线性空气静力分析。分析时,设计方案桥简化为空间杆系结构有限元模型,桥面主梁采用鱼骨梁计算模型,桥面主梁和桥塔采用空间梁单元模拟,斜拉索采用空间杆单元模拟,斜拉索与桥面主梁间采用刚臂单元模拟。桥面主梁考虑静力三分力的作用,由于设计方案桥主梁的高度、宽度和断面形状基本与泰州长江大桥的主梁断面一致,因此主梁的静力三分力系数采用了泰州长江大桥节段模型风洞试验结果[10];斜拉索和桥塔仅考虑阻力分量的作用,斜拉索的阻力系数为0.8,桥塔的阻力系数为2.0[11]。0°风攻角下,主梁的竖向、横向及扭转最大位移随风速增加的变化趋势如图2所示。
从计算结果可知,主梁的最大竖向位移和最大横向位移均出现在跨中,而最大扭转角则出现在距离跨中200~360m处,并随着风速的增大逐渐向跨中靠拢。

图2 主梁的最大竖向、横向及扭转位移随风速增加的变化趋势Fig.2 Evolutionsof themaximum vertical,lateraland torsionaldisp lacementsw ith increasingw ind speed
从图2可以看到,当风速较小时,主梁各方向的位移都比较小,且随着风速的增大呈现线性增长趋势。当风速增大到一定程度后,主梁的各方向位移都呈现出明显的非线性增长趋势。风速较小时,主梁向下挠曲变形,并在风速约100m/s时达到最大值;此后主梁开始上抬,当风速大于110m/s后,主梁的竖向位移突然急剧增大,表明结构开始丧失稳定性。主梁横向位移和扭转角始终按非线性规律增长,并在风速110m/s左右时出现拐点,此后急剧增大,结构开始丧失稳定性。因此,该桥的静风失稳形态主要表现为主梁空间弯扭耦合的失稳形态,以主梁竖弯和扭转失稳变形为主,牵连着横向弯曲变形,静风失稳临界风速在110m/s左右。
为了从抗风性能角度探讨斜拉桥在超千米主跨桥梁中的适用性,对同等主跨的悬索桥——江阴长江大桥(主跨1 385m)进行了空气静力稳定性分析,桥面主梁的静力三分力系数取自该桥节段模型风洞试验结果[12],0°风攻角下主梁的最大竖向、横向和扭转位移随风速增加的变化趋势及与斜拉桥的比较如图3所示。

图3 同等主跨斜拉桥和悬索桥的空气静力性能比较Fig.3 Com parison of the aerostatic behavior between the cable-stayed bridge and suspension bridgew ith the same main span
从图3可以看到,当风速较小时,斜拉桥和悬索桥的各方向的位移值都比较接近;当风速达到90m/s,悬索桥的竖向、横向和扭转位移都突然急剧增大,结构开始进入失稳状态,此后两者间的位移差值非常大。与斜拉桥相似,悬索桥的静风失稳形态也表现为以主梁竖弯和扭转变形为主的空间弯扭耦合失稳形态,同时牵连着横向弯曲变形。悬索桥的静风失稳临界风速在90m/s左右,而同等主跨的斜拉桥的失稳临界风速则在110m/s左右,可见在同等主跨情况下,斜拉桥的空气静力稳定性比悬索桥更好。从静风性能角度而言,主跨超千米的桥梁适宜采用斜拉桥结构体系。
3.2 空气动力稳定性
本文采用三维非线性空气动力稳定性分析方法[9],在0°和±3°风攻角下对斜拉桥设计方案和江阴长江大桥进行了空气动力稳定性分析,两者的空气动力失稳临界风速的比较如表1所示。分析时,桥面主梁的气动导数分别取用泰州长江大桥[10]和江阴长江大桥的节段模型风洞试验结果[12],并考虑了结构前30阶振型的参与,结构的阻尼比为0.5%。
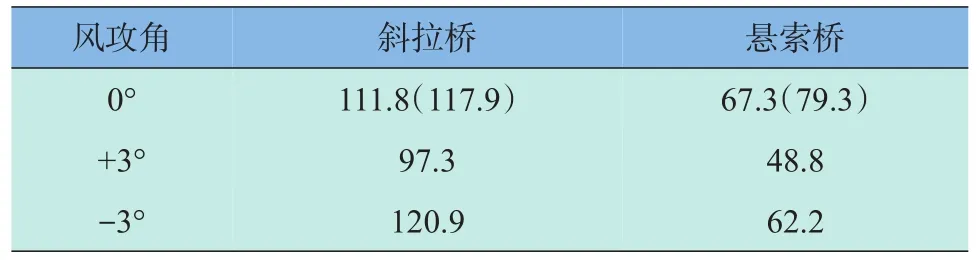
表1 同等主跨悬索桥与斜拉桥空气动力失稳临界风速的比较Table1 Comparison of the criticalw ind speed between the cable-stayed bridge and suspension bridgew ith the samemain span m/s
可以看出,与同等主跨的悬索桥相比,斜拉桥的空气动力失稳临界风速有很大幅度的提高,增加幅度接近1倍。究其原因,这两座桥都呈现一阶正对称竖弯和扭转耦合的空气动力失稳形态,如表2所示,与同等主跨的悬索桥相比,斜拉桥具有更高的竖弯、侧弯和扭转自振频率,尤其是扭转频率提升非常显著,这也说明了在同等主跨情况下斜拉桥比悬索桥具有更大的结构刚度。因此,在超千米主跨情况下,斜拉桥也具有很好的空气动力稳定性,在抗风稳定性方面具有明显的优势。
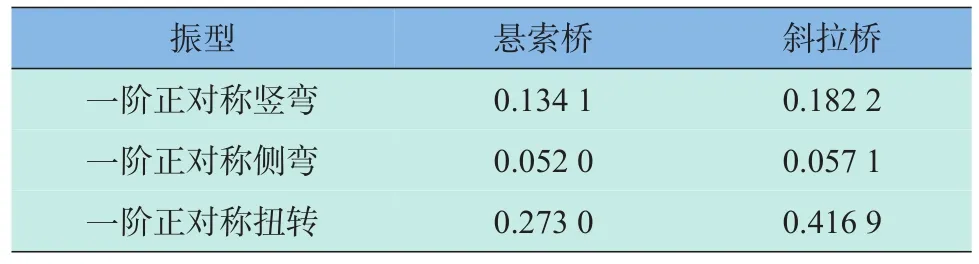
表2 同等主跨悬索桥与斜拉桥的自振频率比较Table 2 Com parison of the natural frequency between the cable-stayed bridgeand suspension bridgew ith the samemain span Hz
4 超大跨度斜拉桥空气静力和动力稳定性的设计参数影响分析
为全面地了解超大跨度斜拉桥的抗风稳定性,分别从主梁的高度和宽度、桥塔结构型式、桥塔高跨比、边主跨比、边跨辅助墩以及斜拉索的锚固体系等斜拉桥主要设计参数着手,对超大跨度斜拉桥的空气静力和动力稳定性的影响进行了分析,并指出了关键的结构设计参数及其合理取值。
4.1 主梁高度
主梁的高度是影响斜拉桥主梁刚度的一个重要参数。在设计方案桥基础上,将主梁高度调整为3m和4m,设计了两座对比方案桥,并进行了空气静力和动力稳定性分析,得到了不同主梁高度情况下主梁的竖向、横向以及扭转位移最大值随风速增加的变化情况。主梁高度对斜拉桥空气动力失稳临界风速的影响如表3所示。

表3 主梁高度对斜拉桥空气动力失稳临界风速的影响Table 3 Effectof the girder depth on the criticalw ind speed of cable-stayed bridge m/s

图4 不同主梁高度下主梁的最大位移随风速增加的变化趋势Fig.4 Evolutionsof them axim um disp lacementsw ith increasingw ind speed under differentgirder depth
从图4可以看到,不同梁高情况下主梁的各向位移随风速增加的变化曲线基本重合,说明主梁高度对该桥的空气静力稳定性影响不大。但在相同风速条件下,梁高的增大可以减小主梁的竖向和扭转位移,并略微增大斜拉桥的静风失稳临界风速。如表3所示,随着梁高的增加,各风攻角下的结构空气动力失稳临界风速都有所提高,说明增加梁高有利于提高超大跨度斜拉桥的空气动力稳定性,但幅度也比较有限。总体而言,增大梁高可以增强斜拉桥的结构刚度,并起到增强斜拉桥抗风稳定性的作用,只是效果比较有限。
4.2 主梁宽度
桥梁主梁宽度是斜拉桥设计的一个重要参数,主要根据设计交通流量确定,但桥面主梁宽度对桥梁结构的抗风性能存在着影响。为探讨主梁宽度对超大跨度斜拉桥抗风稳定性的影响,在设计方案桥的基础上,将主梁宽度调整为28m和32m设计了两座对比方案桥,并进行了空气静力和动力稳定性分析,得出了如表4和图5所示的主梁宽度对斜拉桥空气静力和动力稳定性的影响。

表4 主梁宽度对斜拉桥空气动力失稳临界风速的影响Table 4 Effectof the girder w idth on the criticalw ind speed of cable-stayed bridge m/s
从图5可以看到,梁宽的变化对结构竖向位移影响比较小,但对扭转尤其是横向位移影响却非常显著。在相同风速条件下,随着梁宽的增加,结构的各向位移都在减小,特别是横向和扭转位移,斜拉桥的静风稳定性因而增强。这是由于主梁的竖向刚度与梁宽成正比,而横向刚度则与梁宽的三次方成正比,扭转刚度基本与梁宽的平方成正比,随着梁宽的增加,主梁各方向的结构刚度尤其是横向和扭转刚度明显增大,促使结构静风稳定性提高。因此,增加梁宽有利于提高斜拉桥的静风稳定性。与此相反,如表4所示,斜拉桥的空气动力稳定性却随着主梁宽度的增加逐步降低。考虑到一般情况下结构的空气动力失稳先于静风失稳发生,因此在满足交通需要的前提下,斜拉桥采用较窄的主梁是比较适宜的。
4.3 桥塔结构型式
桥塔结构型式主要指横桥向的结构布置型式,它对斜拉桥的横向和扭转刚度有着重要的影响。为了揭示不同桥塔结构型式对超大跨度斜拉桥抗风稳定性的影响,在设计方案桥基础上,设计了桥塔横桥向倒Y型的方案桥,并进行了空气静力和动力稳定性分析,得到了不同桥塔结构型式下主梁的最大竖向、横向和扭转位移随风速增加的变化情况,结果见图6。桥塔结构型式对斜拉桥空气动力失稳临界风速的影响如表5所示。

图5 不同主梁宽度下主梁的最大位移随风速增加的变化趋势Fig.5 Evolutionsof them aximum disp lacements w ith increasingw ind speed under differentgirder w idth

图6 不同桥塔结构型式下主梁的最大位移随风速增加的变化趋势Fig.6 Evolutionsof themaximum displacements w ith increasingw ind speed under different tower structures
与设计方案桥的A型桥塔相比,斜拉桥采用倒Y型桥塔后,结构的竖向和扭转位移都有所减小,横向位移则基本一致,斜拉桥的静风稳定性因而增强。同样,从表5可以看到,斜拉桥采用横桥向倒Y型桥塔后空气动力失稳临界风速也有所提高。因此,从抗风稳定性而言,斜拉桥采用横桥向倒Y型桥塔更为有利。

表5 桥塔结构型式对斜拉桥空气动力失稳临界风速的影响Table5 Effectof the tower structureon the criticalw ind speed of cable-stayed bridge m/s
4.4 桥塔高跨比
桥塔高度一般是从桥面以上算起,它与斜拉桥的主跨跨径、斜拉索的索面型式、斜拉索索距和倾角有关,对桥梁的整体刚度和经济性等有直接的影响。三跨斜拉桥的桥塔高跨比一般在1/4~1/7,但多数接近于1/5。为了揭示桥塔高跨比对超大跨度斜拉桥抗风稳定性的影响,在其余设计参数不变的情况下,对桥塔高跨比分别为1/6、1/5、1/4的三种情况进行了空气静力和动力稳定性分析,得到了不同桥塔高跨比下主梁的最大竖向、横向和扭转位移随风速增加的变化情况。桥塔高跨比对斜拉桥空气动力失稳临界风速的影响如表6所示。

表6 桥塔高跨比对斜拉桥空气动力失稳临界风速的影响Table 6 Effectof the tower height-to-span ratio on the criticalw ind speed of cable-stayed bridge m/s
从图7可以看出,桥塔高度对结构的竖向和扭转位移影响非常显著,但对横向位移影响很小。在相同风速条件下,结构的竖向和扭转位移随着桥塔高跨比的增大而明显减小,位移的突变点延后,说明结构的静风稳定性得到明显的增强。另一方面,随着桥塔高跨比的增加,斜拉桥空气动力失稳临界风速也有较大幅度提高。因此,增加斜拉桥的桥塔高度,可以明显改善结构的抗风稳定性。
4.5 边主跨比

图7 不同桥塔高跨比下主梁的最大位移随风速增加的变化趋势Fig.7 Evolutionsof themaximum displacementsw ith increasingw ind speed under different tower height-to-span ratios
边跨和主跨的跨径比是影响斜拉桥全桥刚度的一个重要设计参数,大跨度斜拉桥为了减少主跨跨中挠度并提高全桥的竖向刚度通常采用较小的边主跨比,其比值一般在0.25~0.5。为了揭示边主跨比对超大跨度斜拉桥抗风稳定性的影响,在相同主跨情况下,分别对边跨为408m、544m、680m(边主跨比分别为0.29、0.39和0.49)三种情况进行了空气静力和动力稳定性分析。
计算结果显示,不同边主跨比情况的结构各向位移随风速增加的变化曲线基本重合,说明了边主跨比基本不影响斜拉桥的静风稳定性。但仔细对比可知,在相同风速条件下,随着边主跨比的减小,结构的竖向和扭转尤其是横向位移都随之减小,也说明了较小的边主跨比可以提高结构的整体刚度和静风性能。另外,随着边主跨比的减小,斜拉桥的竖弯、侧弯和扭转频率都有所增加,结构的空气动力稳定性因而得到增强,只是提高幅度比较有限。总体而言,边主跨比对斜拉桥的空气静力和动力稳定性影响不明显,但采用短边跨对斜拉桥的抗风稳定性更有利。
4.6 辅助墩设置
斜拉桥为了改善边跨的受力、提高结构的整体刚度和施工安全性通常会在边跨设置辅助墩。为了揭示边跨辅助墩设置对超大跨度斜拉桥空气静力和动力稳定性的影响,以下分别对辅助墩设置的数量和位置两种情况进行了分析。
4.6.1 辅助墩设置数量
为了揭示边跨辅助墩设置数量对超大跨度斜拉桥抗风稳定性的影响,在设计方案桥的基础上,逐步减少边跨辅助墩的数量,分别对辅助墩个数为0个、1个和2个三种情况进行了空气静力和动力稳定性分析。
计算结果表明,辅助墩设置对竖向位移影响比较大,但对横向和扭转位移影响不明显。与不设辅助墩情况相比,设置辅助墩后,静风作用下结构的竖向位移显著减小,竖向位移的突变点延后,说明斜拉桥的静风稳定性得到进一步增强。究其原因,与辅助墩设置的目的是不谋而合的。辅助墩设置后,结构的整体竖向刚度得到了有效的提高,静风作用下结构的稳定性因此增强。但是随着辅助墩设置数量的增加,其起到的增强静风稳定性的效果大大降低,边跨只设置1个辅助墩和设置2个或3个辅助墩所起的作用基本一致。另外,斜拉桥的空气动力失稳临界风速并非随着辅助墩设置个数的增加而单调变化,而是存在着一个最优方案。边跨只设置1个辅助墩时,各风攻角下的空气动力失稳临界风速都比其他工况要高,结构的空气动力稳定性最好。
因此,边跨设置辅助墩有利于提高斜拉桥的空气静力和动力稳定性,但提升效果比较有限,所以辅助墩的设置数量还是要结合经济性和施工安全性等其他因素综合确定。
4.6.2 辅助墩设置位置
如上所述,从抗风稳定性角度而言,斜拉桥边跨只设置1个辅助墩是比较适宜的。为了揭示边跨单个辅助墩设置位置对斜拉桥空气静力和动力稳定性的影响,分别进行了辅助墩设置在距离边跨锚固墩为100m、200m和300m三种情况的分析。
计算结果显示辅助墩设置位置对竖向和扭转位移有较大影响,但对横向位移则基本没有影响。随着离开边跨锚固墩距离的增大,结构的竖向和扭转位移会逐渐减小,静风稳定性逐步得到增强,但辅助墩的设置位置并不是距离锚固墩越远越好,而是存在一个最优的位置。当辅助墩设置在距离边跨锚固墩200m处时,靠近边跨1/3处,结构的各向位移最小,相应地其静风稳定性最好。因此,合理确定辅助墩设置位置可以在一定程度上提高斜拉桥的静风稳定性,但其最优位置需要通过分析来确定。另外,在0°和-3°风攻角下,当辅助墩设置在距离边跨锚固墩300m处时,结构的空气动力稳定性最好,该位置接近于边跨的跨中。综上所述,从抗风稳定性角度考虑,适宜将单个辅助墩设置在边跨跨中附近以获得较好的结构抗风稳定性。
4.7 斜拉索的锚固体系
目前斜拉桥基本都采用自锚体系,即斜拉索全部锚固在桥面主梁上。为了研究斜拉索锚固方式对超大跨度斜拉桥抗风稳定性的影响,在设计方案桥基础上将边跨两侧索面的最外侧5根斜拉索采用地锚,其余29根斜拉索则锚固在主梁上,设计了相应的对比方案桥,并进行了空气静力和动力稳定性分析。
与斜拉索全部锚固在桥面主梁上的自锚体系相比,部分斜拉索采用地锚后,结构的各方向位移都有所减小,说明结构的整体刚度得到增强,结构的静风性能得到提高,只是提升效果并不十分明显。另外,在0°风攻角下,斜拉索采用部分地锚方式后结构的空气动力稳定性要比全自锚式斜拉桥好,而在+3°和-3°风攻角下,两者的空气动力稳定性基本一致。因此,部分斜拉索采用地锚可以增强斜拉桥结构的整体刚度,并可以在一定程度上提高结构的抗风稳定性。
5 结语
本文采用大跨度桥梁三维非线性空气静力和动力稳定性分析方法,对1 400m主跨的超大跨度斜拉桥进行了空气静力和动力稳定性分析,并与同等主跨的悬索桥进行了对比,从抗风性能角度探讨了斜拉桥在超千米主跨桥梁中的适用性。在此基础上,分别就主梁的高度和宽度、桥塔结构型式、桥塔高跨比、边主跨比、辅助墩设置、斜拉索锚固方式等结构设计参数对超大跨度斜拉桥空气静力和动力稳定性的影响进行了分析,并得出两点主要结论。
1)与同等主跨的悬索桥相比,斜拉桥的结构刚度更大,空气静力和动力稳定性更好,适宜采用于超千米主跨的大跨度桥梁。
2)超大跨度斜拉桥在增大主梁高度、减小梁宽、采用倒Y形桥塔并增大塔高、减小边跨长度、边跨设置辅助墩以及部分斜拉索地锚等情况下,都可以获得比较好的空气静力和动力稳定性。
[1] 项海帆.世界大桥的未来趋势——2011年伦敦国际桥协会议的启示[J].桥梁,2012(3):12-16.
[2] 项海帆.进入21世纪的桥梁风工程研究[J].同济大学学报,2002,30(5):529-532.
[3] Gimsing N J.Cable Supported Bridges—Concept&Design(2nd edition)[M].England:JohnWiley&Sons Ltd.,1997.
[4] NagaiM,Fujino Y,YamaguchiH,etal.Feasibility of a1 400m span steel cable-stayed bridge[J].Journal of Bridge Engineering,ASCE,2004,9(5):444-452.
[5] NagaiM,Xie Xu,YamaguchiH,etal.Static and dynam ic instability analysis of 1400-meter long-span cable-stayed bridges[J].IABSEReports,1998,79:281-286.
[6] Kao C S,Kou C H,Xie X.Static instability analysis of longspan cable-stayed bridges w ith carbon fiber composite cable under w ind load[J].Tamkang Journal of Science and Engineering,2006,9(2):89-95.
[7] Kien PH,Yamada H,KatsuchiH,etal.Study on static and dynamic instability of super long-span cable-stayed bridges[C]//The Forth International Symposium on Computational Wind Engineering.Yokohama,2006:777-780.
[8] 孙 斌.超千米级斜拉桥结构体系研究[D].上海:同济大学,2008.
[9] Zhang Xinjun.Influence of some factors on the aerodynam ic behavior of long-span suspension bridges[J].Journal ofWind Engineering and IndustrialAerodynam ics,2007,95(3):149-164.
[10] 陈艾荣.泰州长江公路大桥结构抗风性能研究报告(四)——三塔悬索桥方案节段模型风洞试验[R].上海:同济大学土木工程防灾国家重点实验室,2006.
[11]JTG/TD60-01—2004公路桥梁抗风设计规范[S].北京:人民交通出版社,2004.
[12] 项海帆,林志兴.江阴长江大桥抗风性能研究[R].上海:同济大学土木工程防灾国家重点实验室,1996.
