基于修正Anderson模型的冲击载荷下地基振动响应预测方法

房 波

(中铁八局第二工程有限公司，成都618100)

1 前言

结构在使用过程中可能会承受各种冲击荷载的作用，如结构周围的强夯施工、拆除爆破施工中的结构倒塌触地、爆炸冲击荷载以及意外事件产生的冲击荷载等，冲击荷载作用下产生的地震波会引起结构地基的振动，严重时可使建筑物的正常工作受到影响，甚至导致破坏。因此，结构地基振动效应的预测和控制方法研究已成为土木工程界关注的热点。

冲击载荷作用产生的地震波按照传播路径可分为两部分：震源—结构地基，结构地基—结构内部。结构对地基振动响应的分析方法相对比较成熟，如振型分解反应谱法与时程分析法等。但是，地震波在冲击点至结构地基间的地层中的传播是一个复杂的力学过程，很难用计算方法精确确定。目前关于结构地基在冲击荷载作用下振动特征的研究在爆炸冲击荷载引起的地表振动方面取得了很多成果，主要研究方法包括数值模拟、统计分析与以现场实测为基础的综合预测方法等。

数值模拟方法主要采用商业软件或研究者自行开发的程序模拟土岩介质在爆炸载荷下应力波的传播规律及力学响应特征。Torano等[1]利用有限元法预测爆破振动效应。Chen与Liu等[2，3]用离散元商业软件UDEC模拟了爆炸应力波在节理岩体中的传播过程及露天矿边坡在爆炸载荷下的动力响应。卢文波等[4]通过对爆破地震波传播过程的衰减规律的研究，提出了由典型单孔爆破实测振动波形来确定常规生产爆破情况下，爆源中、远区的爆破振动场的模拟方法。贾光辉等[5]采用非线性有限元分析手段，对爆破地震波对地下结构物的影响进行了数值模拟，分析了介质质点振动速度的传播规律和结构响应特征。通过数值模拟可以得到冲击源附近任意位置的振动特征，但是，岩土介质的力学参数难以确定，并且大多数值方法都是建立在介质均匀化、连续化与各向同性化的基础之上，与实际情况不符，同时又由于数值模拟方法的计算量大，需要技术人员具备一定的数值模拟经验，不便于工程应用。

统计分析方法主要包括基于波形分析方法的经验模型[6]，时间序列预测方法[7]，神经网络模型[8～10]等。Otuonye[7]对大量振动测试数据进行分析，在此基础上，利用时间序列模型预测爆破可能产生的振动效应，即通过实测数据来预测给定爆破设计的振动波形。Chakraborty等[10]通过在露天矿大量爆破实验的基础上，综合分析炮孔直径、抵抗线、单孔装药量、炸药单耗、同段最大药量、测震距离以及振动波形记录等参数，比较分析了不同经验公式的预报结果，在此基础上，建立了神经网络预报模型。统计分析方法思路简单，但是必须通过大量的现场振动测试才能应用，同时适用性差，把某个场地的测试数据用于其他场地时，预测结果与实际结果相差较大。

Anderson等[11，12]通过对多排微差爆破振动波形的模拟研究得出，多排微差爆破的每个炮孔具有相同的源函数，且炮孔的空间分布不影响地震波的传播途径，传播介质的影响可在实测的单孔波形中得到体现。Hinzen[13]利用了在时域内单孔爆破振动信号叠加的优点，综合分析了叠加信号的谱值与相位的变化规律，并据此优化多孔爆破的延期时间。刘军、吴从师通过传递函数法预测结构地基和结构内部的完整波形[14]。刘军等[15，16]提出了考虑爆源与结构之间的地质条件、结构体对不同振动频率的响应的爆破振动动态响应预测模型。但是，上述方法都假设在冲击载荷作用下，介质的振动反应是线性的，这些模型对于冲击能量较小时的振动效应预测结果与实测结果吻合较好，当冲击能量较大时，则不能得到与实测一致的预测结果。

综上所述，结构地基振动效应预测是一项非常复杂的工作，现有的方法都存在不同程度的局限性。在本文的研究中提出了一个理论模型与现场实测相结合的综合预测方法，首先对Anderson模型进行了验证和修正，然后采用修正的模型预测重锤冲击载荷下结构地基振动效应，并通过现场试验对预测方法进行了验证。

2 冲击振动试验

为了验证和修正理论模型，进行了一系列具有针对性的室外冲击振动试验。通过重锤冲击试验装置，对地表施加冲击荷载，利用UBOX-5016爆破振动智能监测仪对距离震源3.8m的结构进行监测。重锤质量17.8 kg，下落高度分别为1m、1.2m、1.5 m、1.8 m，其中1.2 m、1.5 m高度试验重复进行两次。

选取某正方体通风口砖混结构为试验振动监测对象，结构与地基刚性连接，结构中部为一长方体通风窗，顶层用水泥抹灰抹平，如图1所示。试验时，在结构与冲击点之间布置四个测点，如图2所示。在每个测点都分别布置垂直方向与水平径向两个方向的传感器，传感器通过石膏粉等粘结到结构地面或结构上（刚性连接）。

图1 试验结构Fig.1 Experiment al structure

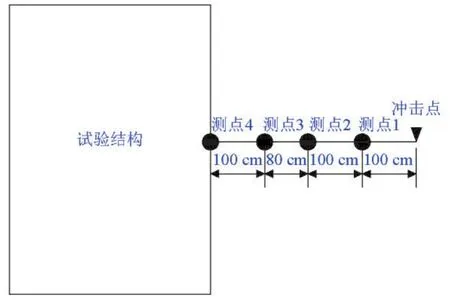
图2 测点布置示意图Fig.2 Sketchmap of monitoring point

3 结构地基振动效应预测

3.1 Anderson模型

Anderson认为，冲击荷载作用下，测点位置的振动u可表示为

式（1）中，m(ξ，τ)为多个冲击源冲击振动的源时间函数；G(x，t，ξ，τ)为弹性动力格林函数；x为测点位置；ξ为冲击源位置；t为时间；τ为格林函数变量。

式（1）表明复杂真实冲击源产生的位移是可由最简单的冲击源产生的位移而合成的，它含有时间源函数。最简单的冲击源是在时间和空间上精确确定的一维单元脉冲，从这样一个简单源产生的位移是弹性动力格林函数。

因此，根据上述Anderson模型的观点，得到简单冲击源ms（单个脉冲）引起地基处的振动为Us：

复杂冲击源m（多个脉冲）引起地基处的振动为U：

其中，复杂冲击源源时间函数m可分为两个部分：

式（4）中mR（第i个脉冲的比例系数ai=Qi/Q0）。

将式（4）代入式（3）再根据卷积的可交换性得：

最后将式（2）代入式（5），得到多个脉冲组成的复杂冲击源在地基处产生的振动预测公式：

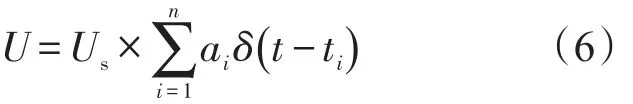
式（6）即为基于Anderson模型下的地基振动预测，其中，Us可通过重锤冲击试验测得，脉冲系列可通过已有的复杂脉冲设计资料方案构造。另外，由上述推导过程可知，式（6）在预测振动效应时对位移、速度以及加速度信号同样适用。

3.2 Anderson模型的验证

3.2.1 给定位置波形可重复性假设的验证

在验证Anderson模型预测结果之前，需对模型的基本假设，即给定位置波形可重复性假设进行验证，以保证模型本身的正确性。采用落锤冲击地面得到结构地基处的波形为简单震源振动波形。试验时选取落锤为1.5m高度冲击下同一冲击点同一测点处重复进行两次，因此两次试验的冲击点位置、冲击能量均相同。用Anderson模型预测冲击载荷下结构地基振动波形。图3、图4为两次冲击试验中在结构-地基处同一测点的两个方向（垂直方向、水平径向）的振动波形记录以及相应的幅值谱。

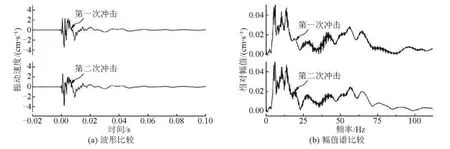
图3 两次冲击下结构-地基垂直方向波形和幅值谱比较Fig.3 Vertical wave form and amplitude spectrum comparison of the structure foundation under twice impact

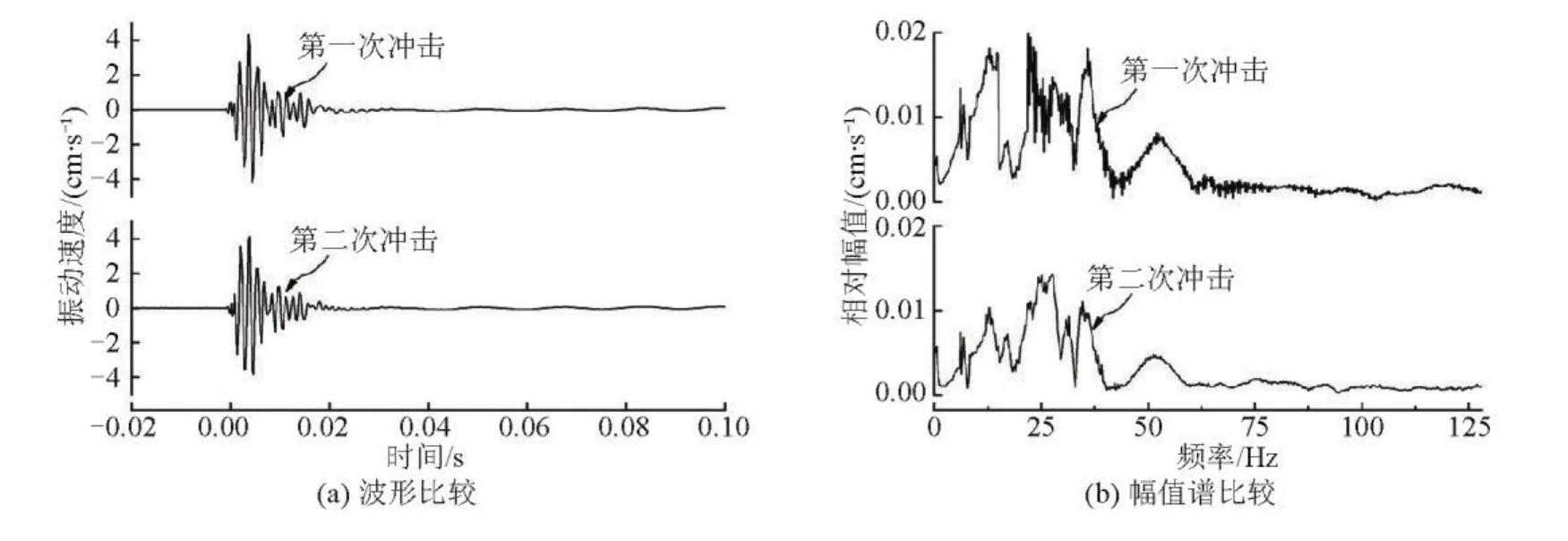
图4 两次冲击下结构-地基水平径向波形和幅值谱比较Fig.4 Horizontal radial waveform and amplitude spectrum comparison of the structure foundation under twice impact

图3和图4表明，在两次相同的冲击载荷下结构地基的同一测点测得的垂直方向和水平径向两个方向的实测波形吻合较好，幅值谱也较接近，只是在高频部分会出现很小的差异，高频部分出现差异主要是因为试验条件以及周围干扰造成的，充分说明了Anderson模型对于简单震源振动波形在给定位置能复现这一假设是成立的。

3.2.2 Anderson模型预测地基振动效应的验证

为了验证Anderson模型的合理性以及对其进行修正，首先利用Anderson模型对重锤冲击试验引起的地基振动进行预测，然后将实测波形和预测波形进行对比分析。选取1.2m高度重锤冲击作为预测其他脉冲振动效应的简单单脉冲冲击源，用以预测重锤1.8m高度冲击下的结构地基振动波形。实测波形、预测波形及其相应的幅值谱如图5和图6所示。

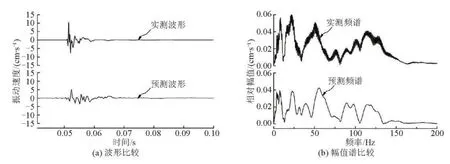
图5 1.8m冲击下结构-地基处垂直方向预测与实测波形和幅值谱比较Fig.5 Vertical waveform and amplitude spectrum comparison between forecast and measured value of the structure foundation under impact of 1.8m high

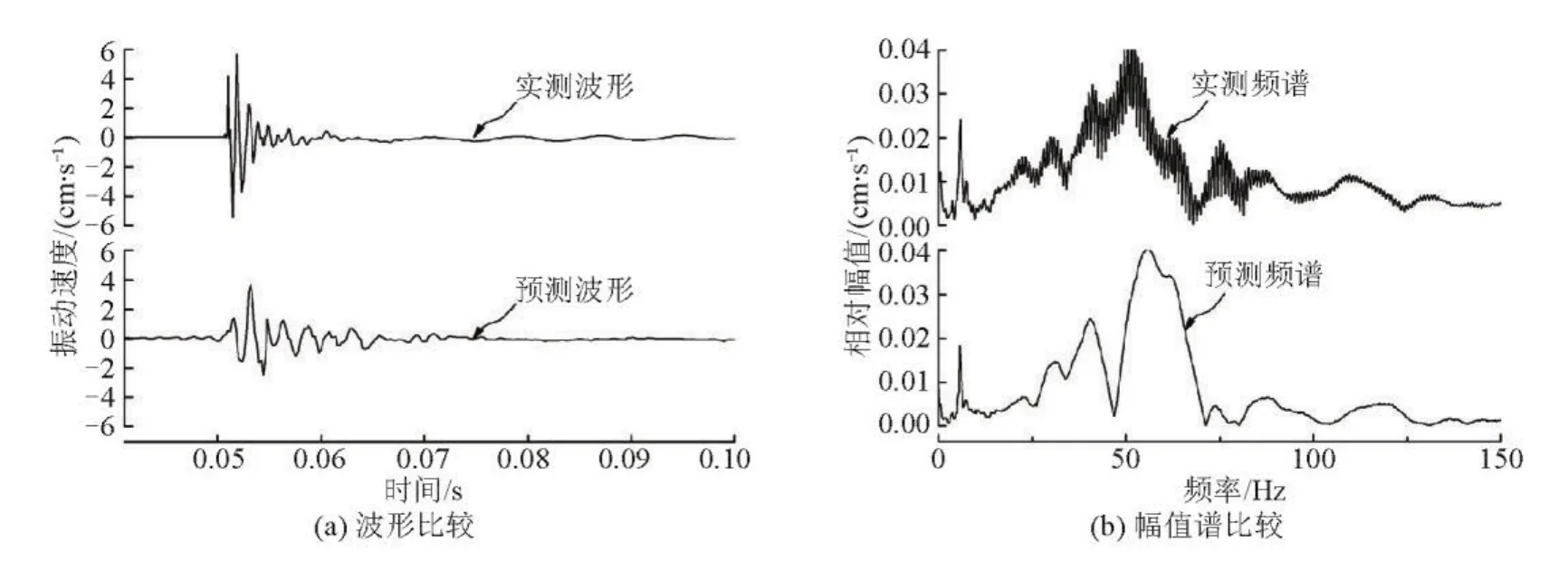
图6 1.8m冲击下结构-地基处水平径向预测与实测波形和幅值谱比较Fig.6 Horizontal radial waveform and amplitude spectrum comparison between forecast and measured value of the structure foundation under impact of 1.8m high

从结构-地基测点的预测与实测波形及幅值谱可以看出：预测波形与实测波形比较相似，吻合较好，说明了Anderson模型是合理的。但是，预测波形的幅度与实测波形的幅度存在比较明显的差异，预测值明显低于实测值，精确度还有待提高，故对模型进行修正是必要的。

3.3 Anderson地基振动预测模型的修正

3.3.1 修正的Anderson模型

通过对试验数据的分析可以看出所预测波形与所选取用来预测的单脉冲之间肯定不是线性关系，为了反映岩土介质在冲击载荷下的非线性特征，对Anderson模型修正如下。

将原来预测公式中地震效应系数αi：

修正为α′i：

以上两个式子中αi为第i个冲击源的地震效应系数；Q0为简单冲击源的势能；Qi为第i个冲击源的势能；α′i为修正后的第i个冲击源的地震效应系数；K和α为反映不同岩土介质力学性能的参数，可根据任意两次重锤冲击试验的波形记录计算得出。

为了得到系数K和α的值，至少进行三次不同冲击势能的简单冲击试验，选取三次中的一次作为预测其他两次脉冲振动效应的单脉冲简单冲击源，所选取的单脉冲简单冲击源的幅值为Q0，另外两次冲击脉冲幅值分别为Q1和Q2，那么修正后的Anderson模型下所预测的两次冲击下波形为：

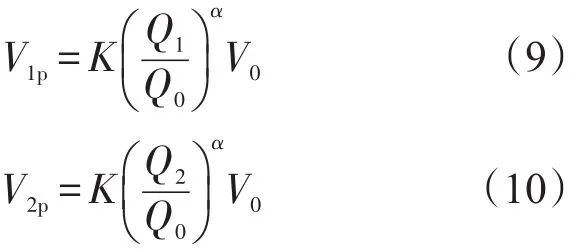
式（9）、式（10）中，V1p和V2p分别为所需预测的脉冲幅值Q1和Q2冲击下的预测波形；V0为单脉冲简单冲击源Q0冲击的实测波形；Q0、Q1和Q2分别为各重锤冲击的冲击势能。

将实测波形值带入预测波形值得到

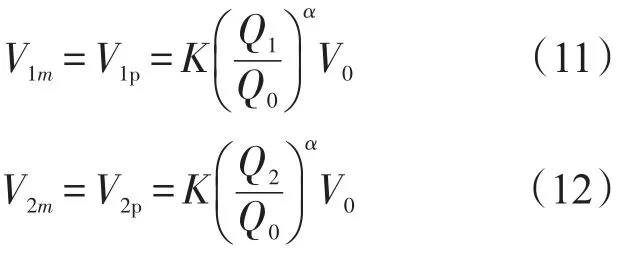
式（11）、式（12）中，V1m和V2m分别为脉冲幅值Q1和Q2冲击下的实测波形。下面选取峰值速度V1和V2为波形参数计算系数K和α，解式（11）得

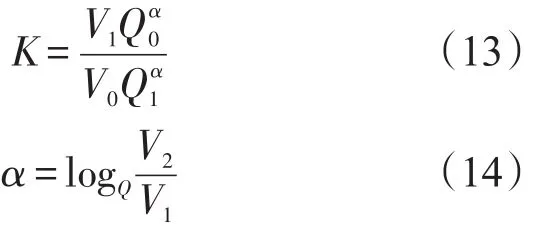
其中Q=Q2/Q1。

因此，得到修正的Anderson预测模型为

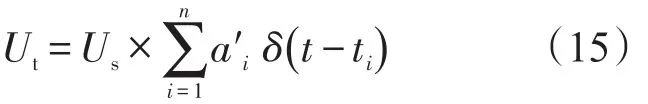
3.3.2 修正的Anderson模型的验证

与Anderson模型的验证类似，选取1.2m高度重锤冲击作为预测其他脉冲振动效应的简单单脉冲冲击源，采用修正后的Anderson模型分别来预测重锤1.8m高度下冲击的振动效应波形。1.8m高度下实测波形、预测波形及其相应的幅值谱如图7和图8所示。

图7 修正模型后结构-地基处垂直方向预测与实测波形和幅值谱比较Fig.7 Vertical waveform and amplitude spectrum comparison bet ween modified model forecast and measured value of the structure foundation

从修正后的Anderson预测结构-地基测点的预测与实测波形及幅值谱可以看出：预测波形与实测波形非常接近，吻合较好，说明了修正的Anderson模型是合理并且有效的。实测与预测波形部分的差异主要是由测量仪器本身或外界高频噪声所致，对结构振动效应预测结果影响不大。

图8 修正模型后结构-地基处水平径向预测与实测波形和幅值谱比较Fig.8 Horizontal radial waveform and amp litude spectrum comparison between modified model forecast and measured value of the structure foundation

4 结语

通过一系列具有针对性的室外重锤冲击振动试验，对Anderson模型进行了验证和修正，并利用修正后的Anderson模型对结构地基振动效应进行了预测，结果表明：修正模型的质点振动速度峰值(PPV值)与实测值非常接近，修正值的精确度提高了约30%，充分说明了修正后的Anderson模型的有效性及准确性，并且能够反映出地震波在岩土介质中传播的非线性特征。本文提出的理论模型与现场实测相结合的综合预测方法可以很好地预测潜在冲击载荷下结构-地基处振动效应。

[1] Torano J，Rodriguez R，Diego I，et al.FEM models including randomness and its application to the blasting vibrations prediction[J].Computers and Geotechanics，2006，33：15-28.

[2] Chen SG，Zhao JA.Study of UDEC modeling for blast wave propagation in jointed rock masses[J].International Journal of Rock Mechanics and Mining Science，1998，35(1)：93-99.

[3] Liu Y Q，Li H B，Zhao J，et al.UDEC simulation for dynamic response of a rock slope subject to explosions[J].International Journal of Rock Mechanics and Mining Science，2004，41(3)：1-6.

[4] 卢文波，王进攻.爆源中远区的爆破振动场模拟[J].爆破，1996，9：10-13.

[5] 贾光辉，王志军，张国伟，等.爆破地震波对地下结构物的影响仿真研究[J].华北工学院学报，2001(6)：445-448.

[6] 霍永基.建筑结构爆破振动效应及安全分析研究[J].爆破，2003，10(1)：1-6.

[7] Otuonye FO.Blast vibration analysis by a time series technique[C].USA：Proc.of Symp.on Exp.and Blast Research，1994：120-125.

[8] 徐全军，刘强，聂渝军.爆破地震峰值预报神经网络研究[J].爆炸与冲击，1999，19(2)：133-138.

[9] 蒋 淳，冯德益.神经网络模型在地震预报中的某些应用[J].中国地震，1994，10(3)：262-269.

[10] Chakraborty A K，Guha P，Chattopadhyay B，et al.A fusion neural network for estimation of blasting vibration[J].Lecture Notes in Computer Science，2004，3316：1008-1013.

[11] Anderson D A，W inaer SR，Ritter A P.Synthetic delay versus frequency plots for predicting ground vibration from blasting[C].Proceeding 3rd Inter.Symp.on Computer Aided Seismic Analysis and Discrimination，1983：52-61.

[12] Anderson D A，Ritter A P，Winzer S R，et al.A method for site-specific prediction and control of ground vibration from blasting[C].Proceeding 11th Annual Conference Explosive and Blast Technique，1985：94-104.

[13] Hinzen K G.Modelling of blast vibrations[J].International Journal of Rock Mechanics and Mining Science&Geomechanical Abstract，1988，25(6)：439-445.

[14] 刘 军，吴 敏，云 斌，等.环境激励下结构振动效应预测方法研究[J].固体力学学报，2010，12：143-150.

[15] 刘 军，吴从师，高全臣.建筑结构对爆破振动的响应预测[J].爆炸与冲击，2002，20(4)：333-337.

[16] 刘 军，吴从师.用传递函数预测建筑结构的爆破振动效应[J].矿冶工程，1998，18(4)：1-4.