拆除爆破数值模拟研究进展

谢先启，刘 军，贾永胜，孙金山

（1.武汉爆破有限公司，武汉430023；2.河海大学土木与交通学院，南京210098）

1 前言

拆除爆破是在清除二战遗留建筑物的背景下兴起的。在城市改建、扩建过程中，拆除爆破以其快捷、简便受到重视，并在拆除市场占据重要的位置。随着这门技术的日臻完善及其带来的显著经济效益，拆除爆破已成为拆除业中最具竞争力的方法之一。在国内，建（构）筑物，尤其是高层建筑物的拆除，主要采用控制爆破技术。目前全国登记注册的爆破公司已有1 000余家，从事爆破行业的工程技术人员达数万人以上，每年进行的拆除工程数千项。面对广阔的市场，城市拆除爆破技术的工程实践及相关理论研究已经越来越受到人们的重视 [1～5]。

目前，拆除爆破的理论研究尚不能满足工程实践需要，原因在于拆除爆破的理论研究具有高度复杂性，这种复杂性主要来自于3个方面：a.炸药的爆轰与结构构件的局部破坏过程描述；b.结构倒塌的复杂力学机理；c.有害效应的预测与控制。早期的研究主要采用简化的解析分析或试验方法，研究结构的失稳判据，即在用爆破方法破坏主要承重构件后，对结构保留部分进行静力学分析，计算或监测预期形成塑性铰部位的应力，确定该部位是否达到屈服，以此判别结构是否倒塌；同时根据构件所能承受的极限荷载确定爆破缺口的位置与高度[1～6]。也有学者尝试采用简化的解析方法求得拆除爆破结构倒塌过程的解析解答[7]，然而由于结构自身以及倒塌过程的复杂性，解析解答很难对实际工程问题给出满意的解释。

随着数值计算和计算机技术的发展，数值模拟技术在拆除爆破领域逐渐得到了应用。近年来，爆破工作者在拆除爆破技术方面做了大量工作，通过计算机仿真分析来优化选择设计参数并对设计结果进行验证已成为共识[8～10]。拆除爆破的数值模拟是按照特定的数学或物理模型，利用计算机进行过程模拟的研究方法，拆除爆破的数值模拟应该满足以下几个方面的要求：a.可以描述结构构件的局部破坏与整体结构的失稳；b.可以预测爆破效果，对于拆除爆破，主要是预测爆破块度分布、爆堆形态（包括爆堆高度、前冲距离、后座距离等）；c.可以根据模拟结果优化爆破设计；d.预测结构倒塌过程。

因此，将计算机模拟技术应用于建筑物拆除爆破，不仅可以了解问题的结果，而且可连续地、动态地、重复地描述事物的发展规律，了解结构整体倒塌与局部断裂破坏的详细过程。同时，还可以把模拟结果中反映的信息反馈给爆破设计，可以修正、完善爆破设计方案，因而拆除爆破仿真模拟技术的研究具有重要的工程应用价值。

拆除爆破的计算机模拟大多以结构倒塌过程为模拟目标。在模拟中，把拆除爆破施工中需要爆破破坏的关键构件按爆破顺序人为移除，这样做的目的在于突出主要矛盾，模拟中主要分析结构倒塌过程中的复杂力学过程以及倒塌范围，这也是拆除爆破施工中最为关心的问题。目前广泛采用的数值方法大体可分为两类：以连续介质力学为基础的连续模拟方法与以牛顿经典力学为基础的离散模拟方法。

2 有限元法

目前用有限元法模拟结构的倒塌过程主要采用商业软件，即对结构的各个构件分别建模，然后采用凝聚力、铰等连接方式给各个相联构件间施加连接以体现结构的整体强度特征，对每个构件进行网格剖分。优点是：可以模拟各个构件在倒塌过程中应力与应变的变化；缺点是：由于有限元是以连续介质力学为基础，不能模拟构件在倒塌与触地过程中的进一步破坏。如Luccioni等采用有限元法分析了恐怖袭击条件下复杂结构在爆炸荷载下的破坏与倒塌过程[11]；Huang等在有限元框架内，以非线性动力学理论为基础，模拟了土耳其伊兹米特大地震中一座115m烟囱的倒塌过程，模拟结果与实际倒塌过程接近[12]；Kaewkulchai与 Williamson 采用梁-柱单元有限元法结合集中塑性模型模拟了平面框架结构的倒塌过程[13]；Lynn与Isobe在有限元中采用ASI-Gauss技术，模拟了简单框架结构的倒塌过程[14]；Möller等采用模糊随机分析方法，在有限元软件框架内，模拟了结构倒塌过程，该方法可充分体现结构构件在倒塌过程中的大变形、接触以及非线性行为，计算效率高[15]；Wang等采用向量式有限元模拟结构倒塌[16]。在我国，也有众多学者利用有限元法模拟结构倒塌过程，这些研究大都以商业软件为框架，如ABAQUS、ANSIS、LS-DYNA等，同时结合多体动力学理论模拟结构倒塌过程[17～23]，如贾永胜等利用ABAQUS有限元软件的非线性瞬态显式动力学模块模拟结构的失稳及倒塌过程[17]，并用该方法对一个拆除爆破实例进行了仿真模拟。模拟结果表明，结构的坍塌过程及爆堆形状与实际接近，如图1所示。

图1 ABAQUS软件模拟结构倒塌过程[17]Fig.1 The simulation results of a structure collapseby the ABAQUS soft ware[17]

有限元方法是建立在连续介质力学基础上的，这也决定了它在模拟结构出现裂纹、裂纹扩展、碎块飞离、结构倒塌大运动等方面的局限性，例如，用有限元来研究材料或结构从连续状态转变为散体状态时（如结构倒塌过程）容易发生网格畸变，从而无法得到正确模拟结果。简言之，有限元模拟可以很好地回答结构是否会倒塌的问题，而在回答结构是怎样倒塌的问题时则存在一些限制。近年来，一些学者为了突破有限元法的局限性，提出了分离式共节点模型，然而，在节点分离的判别以及分离后块体的相互作用等方面还有待进一步研究[24，25]。

3 离散元法（DEM）

自从Cundall提出离散元法[26]以来，离散元法得到了广泛的应用，目前已是岩石力学中针对不连续介质的主要分析方法。离散元法采用动态松弛法求解，用显式中心差分法对运动方程直接进行积分。离散元法与传统的连续介质分析方法如有限单元法、边界单元法、有限差分法相比，其优点是能更为真实地表达求解区域中的几何状态以及大量的不连续面，它比较容易处理大变形、大位移和动态问题。因而适合于模拟结构倒塌的大运动与大变形（见图2）[27，28]。

图2 颗粒元离散元法模拟拆除爆破结构倒塌过程[29]Fig.2 The simulation results of a structure collapse in demolition blasting by DEM with spherical elements[29]

但是，由于结构在破坏前是一个完整的、具有一定强度的整体，用单一的离散元模拟存在很多问题，如传统的离散元法中单元间的接触一般采用开尔文模型，通过该模型体现单元的抗压强度，但是单元的抗拉强度则是通过莫尔-库仑准则中的凝聚力来体现的，而仅仅用凝聚力来体现结构单元的抗拉特性是远远不能体现结构的整体强度特征的。

4 不连续变形分析法（DDA）

DDA是石根华提出的分析块体系统运动和变形的一种数值模型[30]。由于DDA能够计算块体系统不连续面的错动、滑动、开裂及旋转等非连续介质大位移、大变形的静、动力分析等传统有限元方法难以解决的问题，越来越受到爆破界的关注（见图3）。DDA将结构视为非连续块体单元，块体与块体之间用虚拟的弹簧来传递相互的作用力。在我国，有很多学者利用DDA法研究拆除爆破中结构的倒塌过程[31～37]。到目前为止，国内外对于3D-DDA的商业软件尚未出现。

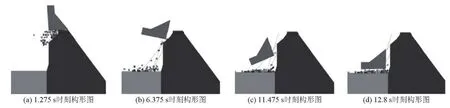
图3 三峡围堰爆破拆除过程的DDA模拟[36]Fig.3 DDA simulation on the demolition blasting of the three gorges cofferdam[36]

5 应用单元法

东京大学Tagel以地震中结构在极端荷载条件下的可视化分析为背景，提出了可以模拟结构的连续与离散力学行为的应用单元法（AEM法）[38～42]。应用单元法中单元间通过各种弹簧连接，即在两个单元的连接节点处分别添加一个法向弹簧与两个切向弹簧，每一组弹簧分别描述一个特定体积介质的受力和变形，如图4所示。弹簧连接对应一定的强度准则，通过单元间弹簧的消失来体现材料由连续转变为散体的过程。应用单元法以单元间分离与开裂为核心，这个核心贯穿结构倒塌的全过程，可以模拟结构从弹性变形、裂纹生成与扩展、强化屈服、单元分离、单元接触碰撞以及单元触地等全过程。从单元间相互作用与运动描述上看，应用单元法近似于离散元法；从求解方式上看，则类似于有限元法。图5为拆除爆破前实际结构与几何模型[43]，图6为拆除爆破结构倒塌模拟与实际结果对比[43]。

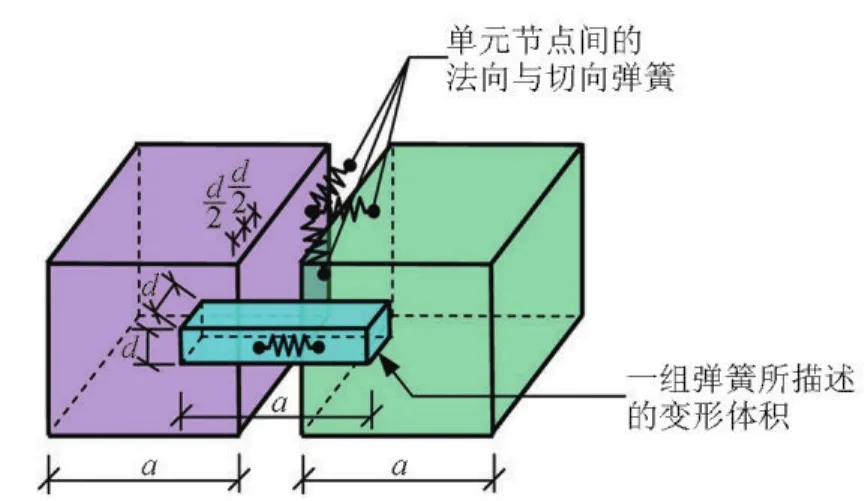
图4 应用单元法中节点间的弹簧联接[38]Fig.4 A group of springs between two neighboring nodes of two elements[38]

6 多刚体动力学与有限差分法

此外还有学者采用多刚体动力学方法模拟结构倒塌过程，如Hartmanna在充分考虑结构倒塌不确定性的基础上，把结构构件间的相互作用分别简化为弹簧阻尼器、圆柱接头、接触等模型，在此基础上，模拟拆除爆破中结构的倒塌过程[44]；Uenishi等采用有限差分法模拟结构在拆除爆破中的倒塌[45]。多刚体动力学方法试用于描述刚体体系的相互作用，用其描述拆除爆破结构倒塌时存在以下问题：a.块体间分离后需要重新调整控制方程；b.当描述大量刚体体系时，计算效率低。有限差分法的理论基础仍旧为连续介质力学，比较而言，在模拟结构倒塌解体时仍旧不能克服以连续介质力学为基础模拟方法的局限性。

图5 拆除爆破前实际结构与结构几何模型Fig.5 Real and simulated structure before demolition

图6 拆除爆破结构倒塌模拟与实际结果对比Fig.6 Comparison of the real collapse configuration and the simulated results by AEM for demolition blasting

7 离散元框架内的网格实体模型

笔者及研究团队针对现有数值方法在模拟拆除爆破结构倒塌过程的缺点与不足，研发了离散元框架内的网格实体模型，并开发了C++计算程序。

网格实体模型是指用多面体单元将研究对象离散化，用接触发现算法确定每个块体单元的邻居单元[46]，并在所有相邻单元间施加“梁”（见图7a），这样在整个介质中就形成了一个“梁”的网络（见图7b）。“梁”的截面形状和大小与公共接触面完全相同，长度为两个单元质心间的距离。每个块体单元为介质粒破碎时的最小单位，块体单元的接触作用及运动由离散单元法描述。

图7 “梁”的变形与单元间的梁网络Fig.7 Deformation of a beam and a beam network between elements

网格实体模型就是通过这个“梁”的网络来体现介质的强度特征。通过单元间的相对位置计算“梁”的变形，根据“梁”的变形情况，判别“梁”是否存在。如果“梁”的变形超过了门槛值，则“梁”消失，两个单元间的联结也随之消失，否则，“梁”依然存在，只发生变形。随着单元间“梁”消失数量的增加，结构损伤逐步累积直至发生破坏，并最终发生倒塌。结构破坏后，会形成众多碎块，其中每一个碎块都包含若干个单元（至少为一个），碎块将会随整个结构体系一起流动，如果碎块包含多个单元，当其受力达到一定程度时，碎块内单元间的“梁”仍有可能消失，所以，碎块可能会分裂成更小的碎块。这就是网格实体模型的基本思路。网格实体模型不仅可以直观体现裂纹及碎块的形成，还可以把有限元中复杂的本构关系及强度理论简化为散粒体间的接触模型及连接的强度判别，并且模拟结果便于可视化。

拆除爆破中结构倒塌过程正是块体元间“梁”逐步消失的过程，由于采用离散元法模拟块体单元间的接触与运动，因而可以体现结构倒塌的大运动过程。同时，用块体元间的“梁”来反映结构的强度特征，可以在单元间传递拉、压、弯、转、扭等各种载荷形式，符合结构的强度特征。因而用离散元框架内的网格实体模型模拟结构的失稳倒塌过程更符合实际情况。为了说明网格实体模型的有效性，图8、图9介绍了用网格实体模型模拟一个结构拆除爆破中结构倒塌的模拟过程。图8为结构的几何模型与实际结构；图9为模拟结果与实际结果的对比。

8 发展趋势

建（构）筑物控制爆破拆除仿真模拟技术是适应建筑拆除行业发展的新技术。在当前城市拆除工程中难度不断加大、机械化作业水平不断提高、工程质量要求更严格的条件下，这种新技术将得到更为广阔的应用，也将产生更为显著的经济效益和社会效益。可以预见，随着人们对拆除技术重要性认识的提高，安全观念的扩大，在我国发达地区、中心城市或者重要部门、特殊场合以及文物风景区的各种建(构)筑物的拆除工程，仿真模拟技术在控制爆破中将得到广泛的应用。然而，由于拆除爆破的复杂性，目前的各种数值方法都存在局限性，合理的、完善的数值方法需要在以下几个方面实现突破。

图8 拆除爆破前实际结构与结构的几何模型Fig.8 Real and simulated structure before demolition

图9 网格实体模型拆除爆破结构倒塌模拟结果与实际结果对比Fig.9 Comparison of the real collapse configuration and the simulated results by the SLM for demolition blasting of a building

1）描述钢筋力学行为的高效计算模型。钢筋在结构梁、柱、板等构件中非常密集，直接影响结构局部承重构件的爆破效果以及结构倒塌过程，如何在数值模拟中建立正确的钢筋单元的力学模型，对数值模拟结果的正确性至关重要。

2）结构关键承重部件的爆破过程模拟。目前的数值方法中普遍采用忽略关键构件爆破破坏过程模拟，而将模拟的重点放在结构倒塌过程方面。因而，一个完善的拆除爆破模拟方法应包含从爆破至倒塌的全过程，只要这样，模拟结果才能为爆破方案的修正提供有价值的参考。

3）拆除爆破有害效应的模拟。安全是拆除爆破的首要问题，如何通过数值模拟结果反映爆破振动、触地振动等有害效应，从而为周边设施的安全防护提供依据，是拆除爆破数值模拟方法发展中不容忽视的重要环节。

[1] Shigeo Kobayashi.An example of the applieation of blasting demolition method to steel-frame building[C]//构造工学论文集，1992.

[2] 卢文波.拆除爆破中裸露钢筋骨架的失稳模型[J].爆破，1992，9（2）：31-35.

[3] Sjoberg CD.拆除爆破高层建筑倒塌过程的研究[C]//第四届国际岩石爆破破碎学术会议.北京：冶金工业出版社，1995.

[4] Tosaka N.Computer simulation for falling Pattems for building[C]//Proceeding of the Third International RILEM Sym Posium，1988.

[5] Stangenberg.Demolition blasting of reinforced concrete industry chimneys[C]//Proeeeding of the IASS-ASCE International Symposium，1994.

[6] Satio T.Blasting demolition of model reinforeed concrete pillars[C]//Proceeding of the Third International RILEM Symposium，1988.

[7] Masoero E，Darò P，Chiaia B M.Progressive collapse of 2D framed structures：An analytical model[J].Engineering Structures，2013，54：94-102.

[8] 孙金山，卢文波.框架结构物拆除爆破模拟技术研究[J].工程爆破，2004，10（4）：1-4.

[9] 汪旭光，于亚伦.21世纪的拆除爆破技术[J].工程爆破，2000，6（1）：32-35.

[10] 贾金河，于亚伦.国外拆除爆破的现状[J].爆破，1998，15（2）：37-41.

[11] Luccioni BM，Ambrosini R D，DanesiR F.Analysis of building collapse under blast loads[J].Engineering Structures，2004，26：63-71.

[12] Huang Wei，Phillip L.Gould 3-D.Pushover analysis of a collapsed reinforced concrete chimney[J].Finite Elements in Analysis and Design，2007，5（5）：1-9.

[13] Kaewkulchai G，Williamson E B.Beam element formulation and solution procedure for dynamic progressive collapse analysis[J].Computers and Structures，2004，82：639-651.

[14] Lynn K M，Isobe D.Structural collapse analysis of framed structures under impact loads using ASI-Gauss finite element method[J].International Journal of Impact Engineering，2007，34：1500-1516.

[15] Bernd Möller，Martin Liebscher，Karl Schweizerh of，ea al.Structural collapse simulation under consideration of uncertainty-improvement of numerical efficiency[J].Computers and Structures，2008，86（19/20）：1875-1884.

[16] Wang R Z，Wu C L，Tsai K C，etal.Structural collapse analysis of framed structures under seismic excitation[R].The 14thWorld Conference on Earthquake Engineering，Beijing，2008.

[17] 贾永胜，谢先启，李欣宇，等.建（构）筑物控制爆破拆除的仿真模拟[J].岩土力学，2008，29（1）：285-288.

[18] 余业清，钟冬望.应用有限元法模拟爆破拆除建筑物倒塌过程[J].武汉科技大学学报（自然科学版），2006，29（5）：513-516.

[19] 余业清，钟冬望，汪 洋.数值模拟在爆破拆除中的应用[J].爆破，2006，23（2）：22-25.

[20] 孙金山，卢文波.框架结构建筑物拆除爆破模拟技术研究[J].工程爆破，2004，10（4）：1-4.

[21] 许 沛，杨 军，安二峰.爆破拆除筒仓构筑物的倒塌过程动态仿真[J].工程爆破，2005，11（4）：8-10，14.

[22] 陈宝心.ANSYS模拟框架结构楼房逐段解体爆破拆除[J].爆破，2004，21（3）：5-7，20.

[23] 任高峰，王玉杰.框架楼房爆破定向倾塌的数值模拟研究[J].工程抗震与加固改造，2005，27（5）：74-77.

[24] 张广荣，池恩安，詹振锵.切口高度对烟囱拆除爆破塌落振动的模拟研究[J].爆破，2013，30（3）：135-141.

[25] 佘 勇，池恩安，赵明生.钢筋混凝土双曲拱桥爆破拆除数值模拟[J].金属矿山，2012（7）：50-55.

[26] Cundall PA，Strack O D.A discrete numerical model for granular assemblies[J].Geotechnique，1979（29）：47-65.

[27] Pekau O A，Cui Yuzhu.Progressive collapse simulation of precast panel shear walls during earthquakes[J].Computers and Structures，2006（84）：400-412.

[28] Gu Xianglin，Wang Xiaolin，Yin Xiaojing，et al.Collapse simulation of reinforced concrete moment frames considering impact actions among blocks[J].Engineering Structures，2014（65）：30-41.

[29] Masoero E，Wittel F K，Herrmann H J，et al.Progressive collapse mechanisms of brittle and ductile framed structures[J].Journal of Engineering Mechanics-ASCE，2010，136：987-995.

[30] Shi G H.Block System Modelling by Discontinuous Deformation Analysis[M].UK：Southampton.Computational Mechanics Publication，1990.

[31] 贾金河，于亚伦.应用有限元和DDA模拟框架结构建筑物拆除爆破[J].爆破，2001，18（1）：27-30.

[32] 贾金河，于亚伦.建筑物拆除爆破数值模拟方法的研究[J].工程爆破，1999，5（1）：47-51.

[33] 王建宙，于亚伦，唐春海.拆除爆破研究中数值分析方法的比较与选择[J].工程爆破，2002，8（1）：8-11.

[34] 赵 根，张文煊.砖烟囱定向拆除与爆破效果DDA数值模拟[J].爆破，2005，22（4）：74-76.

[35] 赵 根，张文煊，李永池.钢筋混凝土烟囱定向爆破参数与效果的DDA模拟[J].工程爆破，2006，12（3）：19-21.

[36] 赵 根，王秀杰，吴新霞，等.三峡三期RCC围堰拆除爆破倾倒效果DDA模拟[J].固体力学学报，2006，27：148-153.

[37] 胡文军，杨艳华.钢结构建筑爆破拆除计算机模拟初步研究[J].工程爆破，2002，8（4）：11-15.

[38] Tagel-Din H，Meguro K.Applied element method for simulation of nonlinear materials：Theory and application for RC structures[J].Structural Eng./Earthquake Eng.，International Journal of the Japan Society of Civil Engineers（JSCE），2000，17（2）：137-148.

[39] Tagel-Din H，Meguro K.Applied element method for dynamic large deformation analysis of structures[J].Structural Eng./Earthquake Eng.，International Journal of the Japan Society of Civil Engineers（JSCE），2000，17（2）：215-224.

[40] Meguro K，Tagel-Din H.Applied element simulation of RC structures under cyclic loading[J].ASCE，2001，127（11）：1295-1305.

[41] Meguro K，Tagel-Din H.AEM used for large displacement structure analysis[J].Journalof Natural Disaster Science，2002，24（2）：65-82.

[42] Meguro K，Tagel-Din H.Applied element method for structural analysis：Theory and application for linear materials[J].Structural Eng./Earthquake Eng.，International Journal of the Japan Society of Civil Engineers（JSCE），2001，17（1）：21-35.

[43] Marin Lupoae，Carmen Bucur.Use of applied element method to simulate the collapse of a building[C]//The Annual Symposium of the Institute of Solid Mechanics and Session of the Comm ission of Acoustics，2009.

[44] Dietrich Hartmanna，M ichael Breidta，Van Vinh Nguyen，et al.Structural collapse simulation under consideration of uncertainty-Fundamental concept and results[J].Computers and Structures，2008（86）：2064-2078.

[45] Koji Uenishi，Hiroshi Takahashi，Hiroshi Takahashi，et al.PC-based simulations of blasting demolition of RC structures[J].Construction and Building Materials，2010（24）：2401-2410.

[46] Schinner A.Fastalgorithms for the simulation of polygonal particles[J].Granular Matter，1999（2）：35-43.