雷达发射机健康状态评价技术研究

钟诗胜，谭治学

(哈尔滨工业大学机电工程学院， 哈尔滨150001)

0 引言

为提高防空雷达系统的保障能力，应在现有维修模式即事后维修的基础之上引入健康管理理念，评估雷达在使用寿命期间的健康程度，从而在更广泛的时间跨度内实现对雷达的状态跟踪。防空雷达组成复杂，故障模式多样，仅靠整机级别的健康状态表述难以得出准确的评价结果，为此，应细化评价对象，针对雷达各分系统分别制定具有针对性的专用评价方法。雷达系统中发射机故障率最高，功能地位重要，应为首要研究对象。其健康状态评价面临两个问题:首先，雷达发射机状态监控参数众多且异构性强，电磁信号参数、机械性能参数、电力参数、热参数深度耦合，采用对各元件进行物理建模的方法，会面临过高的建模代价，并且难以保证模型的鲁棒性。因而，应该寻找一种既能够对异构参数信息统一描述，又能在不同的使用环境下保持其稳定性的方法。目前，仅有系统工程方法可以同时满足这两个特性。其次，雷达发射机健康状态的变化过程是动态的，现在通用的多种系统工程方法缺乏对系统动态特性的准确描述，直接采用此类方法往往难以得出较为准确的结果。通常可在一定理论研究的基础上，利用标准化来解决参数异构性问题。现在被广泛使用的模糊层次分析法拥有一定的改造空间，可对其进行相应的动态特性改造，并利用模糊化方法提高其评价的准确性。

1 雷达发射机健康状态表征

1.1 雷达发射机组成结构及工作过程

本文的研究对象是某型地面防空系统搜寻雷达的集中式全固态发射机。该固态雷达发射机的工作过程如图1所示。发射机接收到激励端传来的射频输入，依靠多级放大固态单元、功率分配器和功率合成器对输入信号进行放大，然后传输给发射单元;循环液冷系统负责对热电路进行冷却;多路并联低压开关电源为每个独立的功率放大组件供电;控制保护系统负责对发射机的状态参数进行监控，并在出现状态异常时启用相应的故障隔离机制保护系统［1］。

1.2 雷达发射机健康状态参数

雷达制造单位在发射机内部布置了大量机内测试装置，支持装备的远程监控和故障诊断，该型发射机在运行过程当中监控的健康状态参数如表1所示。

表1 发射机监控的健康状态参数

这些健康状态参数数量较多且数据构造形式多样，处理方法和数据存储方式难以逐一定制。宜以状态数据的格式为依据，对其进行格式划分后，针对不同格式制定信息提取手段。如表1所示，参照MIMOSA提出的健康状态数据格式定义标准，将雷达发射机的健康参数数据划分为五种:数据序列、数值型数据、波形数据、大型二进制对象、标量值［2］。

2 雷达发射机健康参数的标准化及综合评价技术

数据采集单元收集到的健康状态参数具有不同格式和信息量，不能直接作为健康评价模型的输入信息。因此，在进行健康状态评价之前，需利用健康状态参数的标准化方法实现参数的统一化度量。

为了构建可方便实现工程化转化的健康状态评价模型，考虑将模糊层次分析法和模糊评价方法相结合，构建评价模型的核心算法。模糊层次分析法是系统工程法的一种，采用模糊层次分析法完成综合评价，可有效回避参数耦合问题，亦具有更强的全面性、合理性［3-4］;而模糊评价方法引入了［0，1］区间内的隶属度概念，有助于得到更为精确的评价结果［5］。但传统模糊层次分析法具有两点不足，妨碍了其在雷达发射机健康评价中的应用:

(1)模糊判别矩阵的一致性校对过程繁复，且缺少理论性指导;

(2)传统模糊层次分析法对评价对象的影响因素动态变化跟踪能力不足。

为此，对原有的模糊层次分析方法进行两点改进:借助模糊一致判别矩阵的性质简化其一致性校对过程;在模糊判别矩阵中添加基于影响因素动态特性的权重浮动因子。

2.1 健康状态隶属度向量构建及模型层次结构划分

健康状态隶属度向量是基于参数的劣化程度对装备的健康状态进行映射的基础，其构建应当遵从军方的雷达装备状态划分标准。通过查阅《通用雷达装备质量监控要求》，得知雷达装备的状态评估采用“四级六等”规范［6］。为此，应构建六维装备健康状态参数隶属度向量，分别对应雷达发射机的新品、堪用1、堪用2、堪用3、故障、报废六个状态。

本文层次分析法的层次模型呈三层结构，如图2所示。

图2 综合评价三层模型

底层为参数层;中间层为健康评价指标层，在综合考虑了军用复杂装备的“六性”［2］要求和发射机的保障重点后，选用射频质量、安全性和可靠性构建;顶层为目标层，包含了雷达发射机的健康状态隶属度向量和雷达发射机的健康评价论断。评价过程采用自底向上、逐层综合的方式，不断利用模糊变换算子和因素权重向量来完成信息综合，最终得出顶层的健康评价指标和雷达发射机健康状态的评价结果。

2.2 参数的标准化方法

通过数据采集单元采集上来的原始数据，需经过基于劣化程度的标准化处理，方可被健康评价模型使用。参数的劣化程度指的是参数与完全衰退阈值的接近程度，是其性能衰退程度的模糊化表现形式。该值一般处于［0，1］区间，当其为0表示参数未衰退，而其为1时表示参数已完全衰退。参数标准化的方法便是实现参数状态向［0，1］区间映射的过程。表1已经实现了健康状态参数的格式划分，以此为依据可实现多种格式数据的通用标准化处理。其中，标量值和数值型数据的劣化程度计算过程已在文献［6］中给出，如式(1)所示

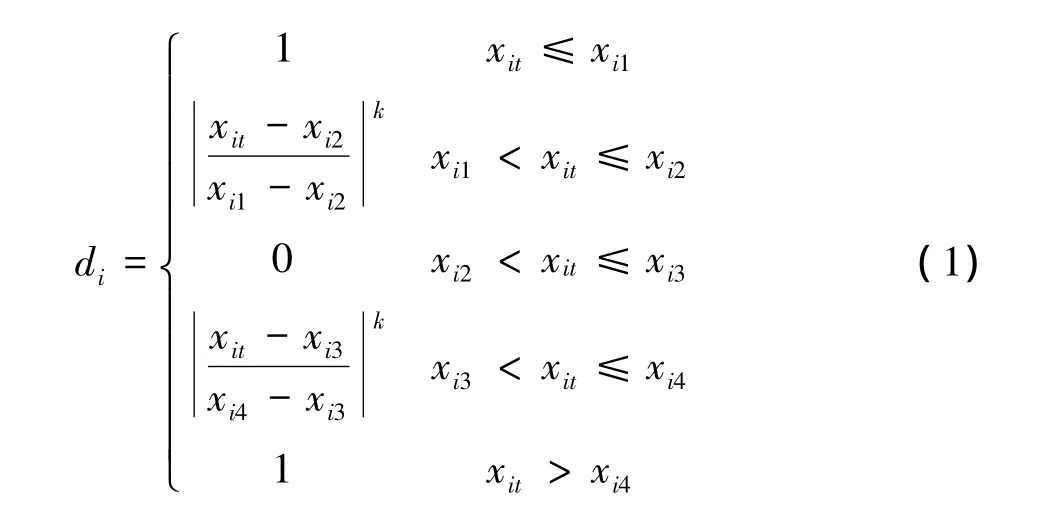
式中:di为参数劣化程度;xit为参数在时间t时的参数值;xi2，xi3分别为参数未劣化状态时的上、下限;xi1，xi4分别为参数的控保机制触发上、下限;k为劣化速率控制因子，反映了指标状态与该因素指标值变化的对应关系［6］，k＞1表示监控人员对参数的较小偏差具有较高的容忍度，反之亦然。k值应该参照参数在不同偏离程度所具有的容忍度而选取，考虑到装备参数一般留有一定的设计余量，因此k值一般应大于1。

鉴于大型二进制文件过于复杂(多为影音文件或特征码文件)且需辨识技术的支持，此处不予讨论;数据序列、大型二进制文件和波形数据的标准化处理需要提取参数特征，而后结合单值型参数的处理方法进行劣化程度计算。

1)数据序列

数据序列是一系列数值的组合(如脉冲序列)，如表1所示，数据序列包含的信息可通过特征提取方法来获取其中的误触发率、漏脉冲和重复频率稳定度特征，通常可对这些特征参数分别设定容忍阈值。而后按式(1)计算特征参数的劣化程度，对特征参数赋予权值并利用平均加权算子进行综合，便可以得出数据序列的劣化程度。

2)波形数据

波形数据劣化程度的计算也需要应用特征提取方法。以雷达发射机的线性脉冲调制信号(如式(2)所示)为例，线性脉冲调制信号的参数评价需要从信号产生和处理过程入手，分析其对线性调频信号的脉冲压缩结果的影响，以实现对脉冲调制信号的劣化程度评价。

式中:s(t)为线性调频信号;Tp为矩形信号宽度;μ为调频斜率。

如图3所示，当脉冲调制信号的波形为理想输入时，脉冲压缩信号为良好的窄脉冲信号;而当输入附带特征参数(如顶降、顶部波动等)扰动的脉冲调制波形后，得到的脉冲压缩信号不但主瓣峰值出现了少许的下降，而且主瓣宽度也有一定加宽，噪声的抑制效果也出现了劣化。

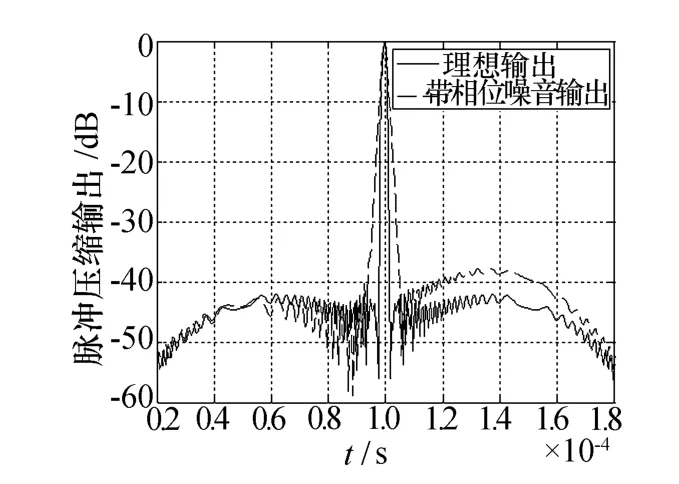
图3 理想脉冲压缩结果及带有调制信号扰动的脉冲压缩结果

脉冲调制信号的劣化程度计算过程如下:首先，提取特征参数:脉冲前后沿、脉冲顶降、顶部波动和脉冲宽度。而后，评估特征参数对脉冲压缩结果的影响:忽略掉雷达反射杂波，直接以雷达发射信号作为脉冲压缩环节的输入。可以发现，脉冲前后沿、脉冲顶降、脉冲顶部波动和脉冲宽度的变化对射频压缩信号的主瓣宽度、信号杂散、旁瓣高度和峰值皆有不同程度的影响，结合数据序列的特征参数处理方法进行加权计算，即可得出脉冲调制信号的劣化程度。

2.3 基于劣化度的浮动权重模糊层次分析法

传统模糊层次分析法的步骤为:(1)建立层次结构模型;(2)建立各层次权重关系判别矩阵;(3)矩阵一致性检验;(4)权重向量求解;(5)实现综合评价。下面将对权重关系判别矩阵的构建、矩阵一致性检验和权重向量求解方法的改进进行讨论。

构建参数的劣化程度隶属度向量，求得所有异构参数的劣化程度后，采用适当的隶属度函数(本文采用三角函数)求得因素劣化程度对应的状态隶属度向量 H1，H2，…，Hs。

2.3.1 建立各层次重要性对比矩阵

对因素的重要程度进行估计，根据层次分析法的判别矩阵构建方法，分别构建每次层次评价过程的多个重要关系对比判别矩阵 B1，B2，…Bs［6］。为了能更精确地阐述权重关系直观判别［7］，采用指数标度代替原本的1-9线性标度构建权重关系判别矩阵，采用的指数标度如表2所示。

表2 指数标度的重要关系判别表

2.3.2 矩阵一致性检验

在得到权重关系判别矩阵后，通过模糊一致判别矩阵和一致判别矩阵的转换关系，将多个权重关系判别矩阵 B1，B2，… ，Bs转换为模糊判别矩阵 F1，F2，…，Fs。

模糊判别矩阵反映了专家对因素重要程度的直观认识，首先满足单个专家的逻辑一致性，获取单一专家的模糊一致判别矩阵，流程如图4所示。

图4 单一专家模糊一致判别矩阵获取流程

1)单一模糊判别矩阵的一致性检验

模糊一致矩阵性质推论:非负互补矩阵F是模糊一致矩阵的充要条件，F的任意两行之间的差向量的元素为固定值［8］。本文将利用此项性质简化一致性检验过程。

(1)m＜n

p为重要性划分界限，一般取p=0.5。

提取由该 m个元素组成的子矩阵 Cm×m，因 Cm×m维度数较小，其一致性较易保证。下面将利用此子矩阵C对整个重要关系对比矩阵进行修改:

(1)选取Cm×m矩阵当中的任意一行L1，选取第m+1行的对应部分L1×m与L1做差，若得到的差向量中所有的元素均为常数a，则将L1×m及其所对应的列加入 Cm×m当中(此时子矩阵扩展为 C(m+1)×(m+1))，否则搁置该因素，留待修正时取用，重复步骤(1)直至遍历矩阵所有行。

(2)取出步骤(1)剩下的元素，按行和降序选取行与子矩阵的任意一行做差，若差向量中大部分元素都为常数a，而其中某些元素ak=rli-rki≠a，则需修改重要程度对比元素rki，令r'ki=rki+(ak-a)，重复直至子矩阵维数扩展为n。

2)多矩阵信息综合

得到多个模糊一致判别矩阵 F1，F2，…，Fs后，通过拟优一致矩阵的方法［9］实现多个专家意见的综合，并将综合得出的模糊一致判别矩阵F作为基准模糊一致判别矩阵，留待健康评价时取用。

2.3.3 求得一致矩阵特征向量

为表述装备参数的动态变化特性，改进的模糊层次分析方法在对矩阵特征向量求解之前，动态地修正了2.3.2节得出的基准模糊一致判别矩阵。参照浴盆曲线和大量装备使用经验得知，装备状态参数在接近失效阈值时，偏差数值和故障率的增长曲线近似于指数函数［10］。因此，赋予层次分析法以劣化程度作为自变量的指数函数形式的浮动权重来模拟这种参数变化趋势，令

式中:e0为参数处于未劣化状态时的重要程度度量;e(di)为参数劣化程度为di时对应的重要程度;Pi为权重浮动因子，取决于该因素的前向耦合因素数量及参数达到或超过容忍阈值的严重程度。

式(3)的解释为:当某项健康状态参数劣化较严重时，其对系统健康程度的影响相对于其他未劣化参数得到了增强，而该影响趋势体现在模糊一致判别矩阵中时，可得

式中:fij(di)为某项参数出现劣化时的模糊判别矩阵对应元素;fij(0)为参数未出现劣化时的模糊判别矩阵对应元素。

同理，将单一因素的影响作用扩展到整个因素集，得出模糊修正矩阵

易证，修正后的模糊矩阵F＇仍然具有一致性。值得注意的是，修正矩阵可能会扩大极重要因素和非重要元素的权重差异，使修正后的模糊一致矩阵出现负元素，对应的解决方法为修正标度上限M的数值，令

式中:Pi0为修正矩阵中最大元素revi0j0的影响变动因子。修改模糊矩阵F＇为 F″

式中:D为全1矩阵。

易证，F″相对于F＇并未有权重判别性质的变化。整个2.3.3节中所描述的基准模糊一致矩阵的取用与修正流程如图5所示。

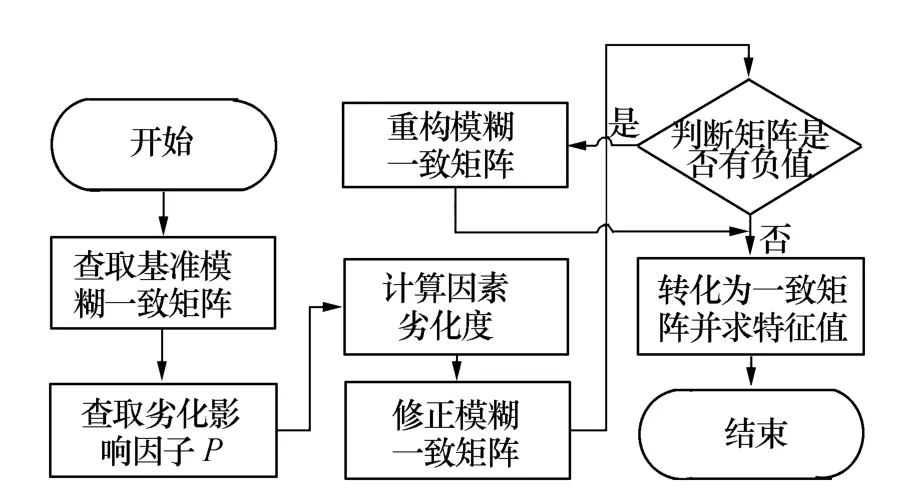
图5 基准模糊一致矩阵取用与修正流程

获得修正模糊一致矩阵F″后，将其转化为一致判别矩阵［11］，并利用最大特征值法求出中间层的指标权重向量A和参数层的参数权重向量AⅠ、AⅡ、AⅢ。

模糊层次分析法的最后一个步骤为:结合层次权重向量，选用模糊变换算子逐层向上得出综合评价结果。模糊变换算子有四种类型［11］，本文在示例中选用加权平均型算子进行隶属度向量综合计算。

3 应用示例分析

出于实际使用数据的种类多样性和篇幅的考虑，本文不给出雷达发射机的参数标准化方法的对比验证实例，仅对改进的模糊层次分析方法进行验证。现针对雷达发射机的数个故障实例给出多个健康状态参数劣化程度序列(共计六种故障模式，故障编号分别为①～⑥)，部分数据如表3所示。

表3 部分健康状态参数(模拟数据)

从表中得知，不同的故障模式体现出了不同的参数劣化程度差异:当冷却单元故障时，机内电路超温，发射机的健康指标呈现出整体劣化趋势;当激励组件出现故障时，仅有个别参数表现出严重的劣化趋势;当个别功放组件发生故障时，发射机整体功率和效率有所下降，体现出较为平缓的性能衰退。

通过专家对评价指标体系的权重评估，得到的指标层的射频质量、安全性和可靠性权重向量为

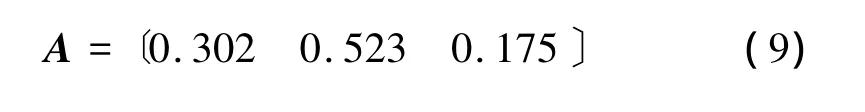
借助专家对参数和指标的权重评定结果，分别利用传统层次分析法和改进的模糊层次分析法对上述故障情形进行健康状态评价，状态隶属度向量如表4所示。

表4 传统层次分析法与改进模糊层次分析法得出的隶属度向量

按照隶属度最大原则，得出雷达发射机的健康状态评价结果，与雷达发射机的故障标准评级结果对比，如表5所示。

表5 传统层次分析法、改进方法评价与标准故障评级结果比较

从分析结果可以看出，传统的层次分析法在参数劣化趋势较一致时可得出较为准确的评价结果，但在仅个别重要指标出现较为严重的劣化时，由于其缺少模型动态修正能力，给出了过于保守的评价结果;而改进的方法通过对权重矩阵进行基于劣化程度的权重修正，获得了更为灵活的动态过程跟踪特性，在参数劣化趋势较一致和差异较大情况下皆能给出较为准确的健康评价结果。

可见，改进的层次分析方法赋予了健康评价模型时变的特征，使其能够更为精确地跟踪劣化的参数或指标对雷达发射机健康状态的影响。该方法已经在国内某型雷达发射机的健康评价问题上证实了其应用价值。

4 结束语

雷达发射机健康状态评价方法的研究具有重要的科研意义和实用意义，本文重点对雷达发射机的健康状态异构参数处理方法和健康评价模型构建方法进行了讨论，并给出了两个问题的解决方法:通过参数的格式划分和参数基于劣化程度的标准化，有效地解决了参数异构问题，为多元参数信息的提取和综合提供了解决方案;通过构建包含健康评价指标、健康状态参数的层次分析结构，有效地回避了物理建模方法的高建模代价以及多元回归方法可能面临的模型复杂性和稳定性问题。同时，本文利用模糊一致判别矩阵的性质简化了其一致性校对过程，并在模糊一致判别矩阵当中引入权重浮动因子以改善其动态评价特性，给出了实例验证过程。结果表明，与传统层次分析法相比，该方法具有更高的健康状态评价精度，且方法灵活性更强。

［1］ Ostroff E D，Borkowski M，Thomas H，et al.固态雷达发射机(下)［J］.陈树铮译.现代雷达，1991(5):90-105.Ostroff E D，et al.Solid-state radar transmitters［J］.Chen Shuzheng translate.Modern Radar，1991(5):90-105.

［2］ Sun Bo，Kang Rui，Xie Jinsong.Research and applicaiton of the prognostic and health management system［J］.Systems Engineering and Electronics，2007，29(10):1762-1767.

［3］ 宾光富，李学军，Dhillon B S，et al.基于模糊层次分析法的设备状态系统量化评价新方法［J］.系统工程理论与实践，2010，30(4):744-750.Bin Guangfu，Li Xuejun，Dhillon B S，et al.Quantitative system evaluation method for equipment state using fuzzy and analytic hierarchy process［J］.System Engineering:Theory＆ Practice，2010，30(4):744-750.

［4］ 宾光富，李学军，李 萍.一种构建机械设备健康状态评价指标体系的方法研究［J］.机床与液压，2007，35(12):177-179，182.Bin Guangfu，Li Xuejun，Li Ping.A new method to establish index system of mechanical equipment healthy state evaluation［J］.Machine Tool ＆ Hydraulics，2007，35(12):177-179，182.

［5］ 李创起，景国勋，张永强.模糊评价方法在煤矿安全管理中的应用［J］. 安全与环境工程，2012，19(1):87-89，94.Li Chuangqi，Jing Guoxun，Zhang Yongqiang.Application of fuzzy evaluation methods to coal mine safety management［J］.Safety and Environment Engineering，2012，19(1):87-89，94.

［6］ 黄建军，杨江平，房子成.基于AHP和模糊评判的雷达系统状态综合评价［J］. 现代雷达，2011，33(3):12-16，33.Huang Jianjun，Yang Jiangping，Fang Zicheng.Radar system state comprehensive evaluation based on AHP and fuzzy［J］.Modern Radar，2011，33(3):12-16，33.

［7］ Zhang Qi，Nishimura T.A method of evaluation for scaling in the analytic hierarchy process［C］//1996 IEEE International Conference on Systems，Man，and Cybernetics.Beijing:IEEE Press，1996:1888-1893.

［8］ 陶余会.如何构造模糊层次分析法中模糊一致判断矩阵［J］.四川师范学院学报:自然科学版，2002，23(3):282-285.Tao Yuhui.How to make fuzzy consistent judgement matrix of the FAHP［J］.Journal of Sichuan Teachers College:Natural Science，2002，23(3):282-285.

［9］ 林卫国，杨明忠.三角模糊AHP在供应商选择中的应用［J］. 河南纺织高等专科学校学报，2005，17(4):22-23，27.Lin Weiguo，Yang Mingzhong.Application of triangle fuzzy AHP algorithm in provider selection［J］.Journal of Henan Textile College，2005，17(4):22-23，27.

［10］ Gebraeel N，Lawley M，Liu R，et al.Residual life predictions from vibration-based degradation signals:a neural network approach［J］.IEEE Transactions on Industrial E-lectronics，2004，51(3):694-700.

［11］ 韦振中.一致判断矩阵与一致模糊矩阵的关系［J］.广西民族学院学报:自然科学版，2001，7(2):87-89.Wei Zhenzhong.The relationship between the consistent judgement matrix and the consistent fuzzy matrix［J］.Journal of Guangxi University for Nationalities:Natural Science，2001，7(2):87-89.